Artículos técnicos

 

Sobre la descripción de las transferencias de masa y energía en sistemas de drenaje agrícola con las ecuaciones de Richards y Boussinesq

 

Description of mass and energy transfers in agricultural drainage systems with the Richards and Boussinesq equations

 

Manuel Zavala¹, Heber Saucedo² y Carlos Fuentes³

 

¹ Universidad Autónoma de Zacatecas, México.

² Instituto Mexicano de Tecnología del Agua.

³ Universidad Autónoma de Querétaro, México.

 

Dirección institucional de los autores

Dr. Manuel Zavala
Universidad Autónoma de Zacatecas
Av. Ramón López Velarde 801, Col. Centro
98060 Zacatecas, Zacatecas, México
Teléfono: +52 (492) 9239 407, extensiones 1617 y 1625
Fax: +52 (492) 9256 690, extensión 6049
mzavala73@yahoo.com.mx

Dr. Heber Saucedo
Instituto Mexicano de Tecnología del Agua
Paseo Cuauhnáhuac 8532, Col. Progreso
62550 Jiutepec, Morelos, México
Teléfonos: +52 (492) 3293 600, extensión 443
Fax:+ 52 (777) 3293659
hsaucedo@tlaloc.imta.mx

Dr. Carlos Fuentes
Universidad Autónoma de Querétaro
Facultad de Ingeniería
Centro Universitario, Col. Las Campanas
76010 Querétaro, Querétaro, México
Teléfono y fax: +52 (442) 1921 200, extensión 6036
cfuentes@uaq.mx

 

Recibido: 30/11/09
Aceptado: 04/05/12

 

Resumen

Se analizan dos modelos mecanicistas para simular el funcionamiento hidráulico de un sistema de drenaje agrícola subterráneo; el primer modelo resuelve la ecuación de Richards sobre un dominio bidimensional, usando una condición de frontera tipo radiación no lineal en el perímetro del dren; el segundo modelo aplica la ecuación de Boussinesq con coeficiente de almacenamiento variable en un dominio unidimensional, imponiendo en los drenes condiciones de frontera de radiación fractal. Se evalúa la capacidad de descripción de ambos modelos de simulación, considerando el caso de un acuífero libre somero con recarga vertical nula, obteniéndose que la aproximación basada en la ecuación de Richards proporciona mejores descripciones de los procesos de transferencia de masa y energía que ocurren en los sistemas de drenaje agrícola, y que la ecuación de Boussinesq no puede describir simultáneamente las transferencias de masa y energía descritas con la ecuación de Richards. Se muestra, por una parte, que cuando el modelo de Boussinesq se usa en la resolución de problemas inversos para estimar la conductividad hidráulica a saturación del suelo (K_s), se obtienen valores para este parámetro mayores a los calculados con el modelo basado en la ecuación de Richards. Por otra parte, se denota que cuando K_s es estimada a partir del modelo de Richards y el valor así obtenido es usado en el modelo de Boussinesq para estimar la separación entre drenes, se obtienen separaciones más cortas de lo necesario.

Palabras clave: flujo de drenaje, radiación no lineal, radiación fractal, coeficiente de almacenamiento variable, abatimiento de la superficie libre.

 

Abstract

Two mechanistic models to simulate water flow in a subsurface drainage system are analyzed. The first model solves the Richards equation on a two-dimensional domain using a nonlinear radiation condition for the perimeter of the drains. The second model uses the Boussinesq equation with the variable storage coefficient on a one-dimensional domain, applying fractal radiation boundary conditions to the drains. The descriptive capacity of both simulation models was evaluated, considering the case of a free shallow aquifer with null vertical recharge. The results indicate that the approach using the Richards equation provides better descriptions of mass and energy transfer processes in agricultural drainage systems and the Boussinesq equation cannot simultaneously describe the mass and energy transfers described with Richards equation. It is shown that when the Boussinesq model is used to solve inverse problems to estimate hydraulic conductivity at soil saturation (K_s), the values obtained are greater than those calculated with the Richards equation model. In addition, when K_s is calculated using the Richards model and the value obtained is used in the Boussinesq model to calculate the separation between drains, separations are obtained that are shorter than necessary.

Keywords: drainage flow, nonlinear radiation, fractal radiation, variable storage coefficient, water table drawdown.

 

Introducción

Una de las funciones básicas de los sistemas de drenaje agrícola subterráneos es evitar el establecimiento de un régimen de humedad adverso para el desarrollo de los cultivos, mediante el abatimiento de mantos freáticos someros y el desalojo oportuno de los excesos de agua provenientes de sobre-riegos, precipitaciones, pérdidas por infiltración en canales y aportaciones de corrientes subterráneas. Para realizar una evacuación eficiente del agua es indispensable conocer cómo se mueve en el suelo, ya que esto permite determinar la evolución del caudal de agua que puede ser removido del medio poroso mediante drenaje y la variación correspondiente del manto freático.

La determinación de las variables de un sistema de drenaje agrícola requiere del análisis de las transferencias de masa y energía que ocurren en el suelo; el estudio de estas transferencias, aunque es altamente complejo, dado que se trata de analizar procesos básicamente no lineales que ocurren en un medio cuyas propiedades varían en el tiempo y en el espacio, puede realizarse considerando alguna de las tres escalas de análisis siguientes:

Escala microscópica. En esta escala de análisis, que corresponde a cada poro del suelo, la velocidad media del agua o gasto microscópico unitario se estima con la ecuación de Poiseuille, la cual proviene de las ecuaciones de Navier-Stokes, y la presión en cada poro se estima con la ecuación de Laplace. Esta escala de análisis es recomendable para una comprensión fina de los mecanismos fundamentales de los procesos de transferencia.

Escala macroscópica. La complejidad que plantea la definición precisa de la forma geométrica del espacio poral hace que la descripción microscópica no pueda ser puesta en práctica sin un cambio de escala, cuya etapa esencial consiste en introducir el concepto de volumen elemental representativo, el cual permite establecer una equivalencia entre el medio real disperso y un medio ficticio continuo. En esta escala de análisis, que corresponde a un conjunto de poros de amplia gama de tamaños, la velocidad media en los poros llenos con agua o gasto unitario macroscópico se calcula con la ley de Darcy-Buckingham (1907) y la presión del agua asociada al conjunto se calcula con la propia ley de Laplace aplicada al tamaño de poro mayor; la ecuación de transferencia correspondiente es conocida como ecuación de Richards (1931).

Escala megascópica. En esta escala de análisis, que corresponde a un conjunto de suelos, la velocidad media o gasto unitario megascópico se estima con la ley de Darcy promediada, considerando la hipótesis de Dupuit-For-cheimer, concerniente a una distribución hidrostática de presiones, y la presión del agua es la proporcionada por los piezómetros; la ecuación de transferencia correspondiente es conocida como ecuación de Boussinesq del drenaje agrícola.

En la práctica, el análisis del drenaje agrícola es realizado con la ecuación de Richards (p.e., Zaradny y Feddes, 1979; Fipps y Skaags, 1986; Saucedo et al., 2002), o con la ecuación de Boussinesq del drenaje agrícola (p.e., Dumm, 1954; Pandey, et al., 1992; Gupta et al., 1994; Samani et al., 2007). La primera ecuación diferencial permite realizar descripciones de los procesos de transferencia que ocurren en las zonas saturada y no saturada del suelo; sin embargo, su aplicación a la escala de un distrito de riego e incluso de la parcela se ve limitada tanto por la dificultad y el costo del trabajo experimental requerido para representar las características hidrodinámicas del suelo (curva de retención de humedad y curva de conductividad hidráulica) como por el esfuerzo de cómputo necesario para modelar el movimiento tridimensional del agua en el suelo. Estas limitantes han originado que el estudio de los procesos de transferencia de agua en los sistemas de drenaje agrícola sea principalmente realizado con la ecuación de Boussinesq, aproximación que si bien considera de manera simplificada las transferencias que ocurren en la zona no saturada del suelo, es una herramienta útil para hacer descripciones aproximadas del flujo del agua en el espesor saturado del medio poroso.

Recientemente se han presentado dos modelos mecanicistas para el drenaje agrícola, que mejoran las hipótesis tradicionales de los modelos reportados en la literatura. Por una parte, Zavala et al. (2005) han desarrollado un modelo para el drenaje agrícola subterráneo basado en la ecuación de Richards bidimensional, sujetando esta ecuación diferencial en la frontera del dren a una condición de radiación no lineal, con la cual las transferencias de masa y energía en un sistema de drenaje son mejor representadas. Por otra parte, Zavala et al. (2004) y Fuentes et al. (2009) han estudiado el drenaje agrícola con la ecuación de Boussinesq y deducido, respectivamente, el tipo de condición de frontera que debe usarse en los drenes agrícolas con esta ecuación, y la relación entre la curva de retención de humedad y el coeficiente de almacenamiento en acuíferos libres someros.

El objetivo de este trabajo es aplicar los dos modelos ya descritos para evaluar y comparar las transferencias de masa y energía obtenidas con las ecuaciones de Richards y Boussinesq, así como identificar el efecto de las hipótesis consideradas en la derivación de la ecuación de Boussinesq sobre las descripciones que proporciona esta relación.

 

Materiales y métodos

Escala macroscópica

El movimiento del agua en el suelo, y en consecuencia, en un sistema de drenaje subterráneo, es un fenómeno tridimensional, motivo por el cual su descripción debe realizarse usando la ecuación de Richards en tres dimensiones; sin embargo, dado el esfuerzo de cómputo que implica resolver esta forma de la ecuación de Richards, es conveniente aceptar la hipótesis de que el fenómeno es básicamente bidimensional, es decir, que se efectúa en planos perpendiculares a la dirección del dren. Si además se asume que la extracción de agua por las plantas es despreciable, la forma bidimensional de la ecuación de Richards puede escribirse:

donde ψ es el potencial de presión del agua en el suelo [L]; C(ψ)=dθ(ψ)/dψ, la capacidad específica [L^-1]; θ(ψ), el contenido volumétrico de agua [L³L^-3]; K(ψ), la conductividad hidráulica del suelo [LT^-1]; x, la coordenada horizontal [L]; z, la coordenada vertical orientada positivamente hacia abajo [L], y t es el tiempo [T].

Si se considera un sistema de drenaje con tubos paralelos equidistantes instalados a igual profundidad, se puede definir un dominio para la ecuación (1), como el mostrado en la figura 1.

La descripción del drenaje agrícola subterráneo con la ecuación (1) requiere la definición tanto del estado inicial de las presiones en el medio poroso como de las condiciones en la frontera del sistema. El estado inicial de la presión del agua en el suelo se especifica como una función conocida del espacio:

Por la simetría del flujo se sabe que el flujo de Darcy en dirección perpendicular a los segmentos AF, DE y BC es nulo (condición tipo Neumann), y una situación similar ocurre en el segmento de frontera CD debido al estrato impermeable:

donde P_E es la profundidad del estrato impermeable, medida a partir de la superficie del suelo; y L es la separación entre drenes.

En la superficie del suelo (segmento AB), si se conoce la evolución de la evaporación (i), puede imponerse una condición de frontera tipo Neumann:

De acuerdo con Zavala et al. (2005), la transferencia de agua del suelo al dren debe ser descrita con la siguiente condición de frontera de radiación no lineal:

donde es la derivada en la dirección normal a la frontera del dren; q_o, un valor particular del flujo del agua en la interfaz suelo-dren [LT^-1]; α y β, los parámetros de forma adimensionales; P, la profundidad del dren [L], y h_t es la presión en el interior del dren [L] igual a la atmosférica (h_t = 0) en el segmento del perímetro interno del dren en contacto con aire, e igual al tirante de agua que se tenga en cada punto del perímetro interno del dren en contacto con agua.

La aplicación de la relación (7) requiere del conocimiento de la evolución del tirante medio en el dren; si se desprecian las variaciones en el sentido longitudinal, el tirante en el dren puede suponerse uniforme en el espacio, pero variable en el tiempo. En esta situación, la evolución en el tiempo del tirante puede calcularse a partir de una ecuación que relacione la velocidad del flujo con la pérdida de energía en la dirección del movimiento. Se considera, por su generalidad, la ley de resistencia fractal propuesta por Fuentes et al. (2004):

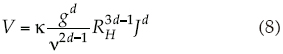
donde V es la velocidad media del agua en el dren [LT^-1]; d, un parámetro adimensional que varía entre 1/2 ≤ d ≤ 1, en función del tipo de flujo (turbulento o laminar); κ, un coeficiente adimensional; g, la aceleración gravitacional [LT^-2]; v, la viscosidad cinemática del agua [L²T^-1]; R_H, el radio hidráulico [L], y J es la pendiente de fricción, que en el caso de flujo uniforme es paralela a la pendiente topográfica del dren J_o [LL^-1].

La combinación de la relación (8) y la ecuación de continuidad para flujo permanente, que indica que el gasto Q es el producto del área hidráulica por la velocidad media del agua (Q = VA), permite obtener la relación entre el tirante medio en el dren y el gasto que conduce . Sin embargo, la aplicación de esta relación presenta una limitante: se tienen dos incógnitas (gasto y tirante) y sólo una ecuación. Este problema se resuelve planteando una segunda ecuación que se obtiene al integrar la condición de radiación no lineal (7):

donde Ω es el perímetro de la semicircunferencia del dren (ver figura 1) y ℓ es la longitud de éste.

Para modelar el drenaje agrícola con el sistema de ecuaciones (1-9), es indispensable disponer de representaciones analíticas de las características hidrodinámicas del suelo θ(ψ) y K(θ). En aplicaciones de campo y de laboratorio, Fuentes et al. (1992) recomiendan usar el modelo para la característica de humedad de van Genuchten (1980), sujeto a la restricción de Burdine (1953):

donde θ_s es el contenido volumétrico de agua a saturación; θ_r es el contenido volumétrico residual, y ψ_d, m y n son parámetros empíricos.

Y para la conductividad hidráulica sugieren el uso del modelo de Brooks y Corey (1964):

donde K_s es la conductividad hidráulica a saturación [LT^-1] y η es un parámetro de forma adimensional positivo.

 

Escala megascópica

Descripciones generales de las transferencias de masa y energía en los sistemas de drenaje agrícola pueden ser obtenidas con la ecuación de Boussinesq. Conforme a la hipótesis de que las variaciones en el sentido del dren son despreciables y la recarga es nula, la dinámica del agua en el espesor saturado del suelo en un acuífero libre somero puede ser descrita con la siguiente forma de la ecuación de Boussinesq del drenaje agrícola:

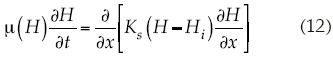
donde H y H_i son, respectivamente, la elevación de la superficie libre y la elevación del estrato impermeable, medidas a partir de un nivel de referencia [L]; cuando el estrato impermeable es aproximadamente horizontal, puede suponerse como el nivel de referencia y tomarse H_i = 0; μ(H) es el coeficiente de almacenamiento [L³L^-3], que en un acuífero libre somero es función de la carga hidráulica (Hilberts et al., 2005; Fuentes et al., 2009).

La consideración del modelo para la curva de retención de humedad de van Genuchten sujeto a la restricción de Burdine y la hipótesis de una distribución hidrostática de presiones permite obtener la siguiente representación analítica para el coeficiente de almacenamiento (Fuentes et al., 2009):

donde H_s es la elevación de la superficie del suelo.

Para resolver la ecuación (12) sobre el dominio de solución mostrado en la figura 2, es indispensable definir las condiciones iniciales y de frontera. La especificación de estas condiciones límites es más conveniente si la posición de la superficie libre contada a partir del estrato impermeable es expresada como:

donde h(x,t) es la carga hidráulica contada a partir de la posición de los drenes y D_o es la profundidad del estrato impermeable medida a partir de los drenes (ver figura 2).

En términos generales, la condición inicial de la presión debe ser especificada como la elevación de la superficie libre a lo largo de la coordenada horizontal x:

Zavala et al. (2004) han mostrado que la relación que debe sujetar a la ecuación de Boussinesq en la frontera de los drenes es la siguiente condición de frontera tipo radiación fractal:

donde γ es un coeficiente de conductancia adimensional; s, el cociente de la dimensión fractal del suelo D_f y la dimensión del espacio de Euclides (s = D_f/3); , la conductividad hidráulica de la interfaz suelo-dren. El signo positivo en la ecuación (16) es tomado para el dren ubicado en la coordenada x = 0 y el negativo para x = L. De acuerdo con Zavala et al. (2007), es conveniente expresar la ecuación (16) en la forma:

donde qs = γ P/L.

La dimensión cociente s está definida implícitamente en función de la porosidad volumétrica (Φ) del objeto fractal (suelo y pared del dren) como:

 

Aplicación

La comparación de las transferencias de masa y energía proporcionadas por los sistemas de ecuaciones (1-11) y (12-17) se realiza considerando la información de experimental de drenaje de Zavala et al. (2004). El experimento realizado en laboratorio consistió en lo siguiente:

a) Construir un contenedor con hojas de acrílico transparente; instalar en éste, a igual profundidad y de forma paralela, dos tubos lisos de PVC con perforaciones circulares en su pared, para representar las ranuras de los drenes agrícolas; rellenar el módulo experimental con una muestra alterada de suelo de textura arenosa de la región de Tezoyuca, Morelos, previamente tamizada (malla de 2 mm) y colocada en capas 20 cm, manteniendo aproximadamente constante la densidad aparente.

b) Tapar la descarga de los drenes y saturar el sistema de drenaje mediante una aplicación de lámina de agua en la superficie del suelo; dejar reposar el sistema hasta alcanzar la estabilidad de la presión del agua en el suelo; cubrir la superficie del mismo con un plástico para eliminar la evaporación, y destapar los drenes para medir el volumen de agua evacuado del suelo.

Las características físicas del sistema de drenaje de laboratorio son L = 1.0 m, P = 1.20 m, D_o = 0.25 m; longitud y diámetro del dren, ℓ = 0.30 m y D_d = 0.05 m, y la pendiente de los drenes J_o = 0.001.

La caracterización hidrodinámica del suelo, realizada de manera independiente al evento transitorio de drenaje, permitió determinar los siguientes valores para los modelos de van Genuchten, y de Brooks y Corey (Zavala et al., 2004): θ_s = Φ = 0.539 cm³/cm³, m = 0.373, η = 3.767, K_s = 0.183 m/h y ψ_d = -0.418 m. Siguiendo la recomendación de Haverkamp et al. (2005), se puede reducir el número de parámetros a determinar en la caracterización hidrodinámica, asumiendo que el contenido volumétrico de agua es cero (θ_r = 0 cm³/cm³), lo cual implica aceptar que cuando ψ → -∞, necesariamente θ → 0. Para estimar el coeficiente adimensional de la ley de resistencia fractal (ecuación (8)), Zavala et al. (2005) asimilan esta ley a la relación de Hazen-Williams, considerando d = 0.54, y determinan κ = 9.83 (drenes de PVC lisos).

Las condiciones experimentales permiten identificar, por una parte, que la condición inicial del evento de drenaje es la de un suelo totalmente saturado, con una distribución hidrostática de presiones y, por otra parte, que todos los segmentos de frontera del dominio, con excepción del asociado al dren, son impermeables. Introduciendo las porosidades volumétrica del suelo (Φ_ms = 0.539 cm³/cm³) y de la pared del dren (Φ_d = 0.017 cm³/cm³) en la ecuación (17), se obtiene el exponente de la condición de radiación fractal (16.1) para la ecuación de Boussinesq . Finalmente, los parámetros α, β y q_o, que intervienen en la condición de radiación no lineal (ecuación (7)) para la ecuación de Richards, así como el parámetro de escala q_s de la condición de radiación fractal que sujeta a la ecuación de Boussinesq en los drenes (ecuación 16.1), son determinados a partir de la evolución en el tiempo de la lámina drenada experimental. Para salvar el problema de estimar tres parámetros a partir de un solo evento, Zavala et al. (2005) asumen α = β, y obtienen α = β = 1.88 y q_o = 300 K_s (este parámetro representa un promedio de la velocidad del agua en los poros grandes de la pared del dren y de la velocidad en los poros del suelo en contacto con el dren); en el caso de la ecuación de Boussinesq, Zavala et al. (2004) reportan q_s = 0.913 K_s.

Para comparar las transferencias descritas con los dos modelos analizados es necesario resolver numéricamente los sistemas (1-11) y (12-17). Ambos sistemas de ecuaciones se solucionan realizando la discretización espacial con el método del elemento finito tipo Galerkin; la discretización temporal, con un método de diferencias finitas implícito, linealizando el sistema resultante con el método iterativo de Picard y resolviendo el sistema de ecuaciones algebraico con un método de gradiente conjugado precondicionado, adaptado para el manejo de matrices almacenadas vectorialmente sin coeficientes nulos. Las particularidades de los métodos están documentadas, por ejemplo, en Zienkiewicz et al. (2005).

La discretización del dominio de solución de la ecuación de Richards bidimensional se realiza aplicando el programa Argus One 4.0p, con el cual se generó una malla de elementos finitos de 10 795 nudos, distribuidos en 21 082 elementos (figura 3), siendo los pasos de espacio mínimos Δx_mín = Δz_mín = 0.2 cm y los máximos Δx_mín = Δz_mín = 2.0 cm. El dominio de solución de la ecuación de Boussinesq unidimensional se discretizó generando una malla de 201 nudos y 200 elementos finitos de tamaño uniforme (Δx = 0.5 cm). La densidad de la discretización espacial de ambos dominios de solución permite tener errores de balance de masa menores del 0.1% en las simulaciones desarrolladas.

Aplicando las soluciones numéricas de los sistemas (1-11) y (12-17), se modela el experimento de drenaje para determinar y comparar la evolución en el tiempo de la lámina de agua evacuada por el dren y la variación correspondiente de la superficie libre a la mitad de separación entre drenes.

Los resultados obtenidos para la transferencia de masa se presentan en la figura 4 y para la transferencia de energía en la figura 5; en ambos casos, conforme el tiempo de drenaje aumenta las evoluciones calculadas, tienden a un valor límite debido a que la recarga es nula.

En la figura 4 se observa un buen acuerdo entre la evolución de la lámina de agua drenada descrita con la ecuación de Richards y la evolución obtenida con la ecuación de Boussinesq (R² = 0.9847), resultado lógico, porque ambas evoluciones son el producto directo de la estimación de los parámetros de las condiciones de radiación (7) y (16.1), a partir de la serie experimental de la lámina drenada. Sin embargo, la evolución del manto freático no fue considerada para optimizar parámetros, por lo que esta variable es un buen elemento de comparación. Observando los resultados mostrados en la figura 5, se identifica una discrepancia importante entre la evolución descrita con el modelo basado en la ecuación de Richards respecto de la evolución obtenida con el modelo de Boussinesq; en todo el tiempo de drenaje, el abatimiento de la superficie libre calculado con Boussinesq es más lento que el obtenido con Richards.

Tomando en cuenta que la ecuación de Boussinesq puede obtenerse integrando la ecuación de Richards en la vertical con la hipótesis de una distribución hidrostática de presiones (Bear, 1972), supuesto que no se cumple en las regiones cercanas al dren, se tiene que la descripción más precisa de la variables hidráulicas en un sistema de drenaje subterráneo corresponde a la proporcionada por la ecuación de Richards. Considerando además los resultados de las simulaciones, se identifica que el modelo basado en la ecuación de Boussinesq (ecuaciones (12) a (17)) no puede reproducir de manera simultánea las evoluciones de las transferencias de masa y energía descritas con el modelo basado en la ecuación de Richards; es decir, si reproduce la evolución de la masa no es factible que reproduzca la evolución de la energía, o si reproduce la evolución de la energía no puede reproducir la evolución de la masa.

La limitante de una descripción simultánea precisa de las transferencias de masa y energía con la ecuación de Boussinesq debe tenerse presente cuando se usa para estimar propiedades hidráulicas del suelo o cuando se aplica al diseño de sistemas de drenaje. Por una parte, es tradicional considerar esta ecuación para estimar la conductividad hidráulica a saturación del suelo a partir de mediciones de abatimiento o recuperación del manto freático; si este es el caso, el valor determinado será mayor al valor real de conductividad hidráulica del medio poroso, pues de acuerdo con los resultados de este trabajo, la ecuación de Boussinesq describe abatimientos menores de los que se presentan en un sistema de drenaje. Por otra parte, si la conductividad hidráulica a saturación del suelo ha sido estimada a partir de pruebas de campo o laboratorio que consideran relaciones más precisas que la ecuación de Boussinesq, y se usa este valor de K_s, en combinación con la ecuación de Boussinesq para calcular la separación entre drenes, se pueden obtener separaciones menores de lo que realmente se necesita para satisfacer el abatimiento del manto freático.

Para ilustrar estas dos situaciones se retienen las descripciones de la prueba de drenaje de laboratorio obtenidas con el modelo de Richards y se realizan simulaciones numéricas con el modelo basado en la ecuación de Boussinesq. Se determina, primero, el valor de conductividad hidráulica a saturación, que permite aproximar con el modelo basado en la ecuación de Boussinesq el abatimiento del manto freático a la mitad de separación entre drenes descrito con la ecuación de Richards. Posteriormente se retoma el valor de conductividad hidráulica a saturación determinado en laboratorio por Zavala et al. (2004), y se calcula la separación entre drenes que requiere la ecuación de Boussinesq, para minimizar las diferencias entre el abatimiento del manto freático que describe a la mitad de separación entre drenes y el abatimiento obtenido con la ecuación de Richards.

Los resultados obtenidos para el primer caso se muestran en las figuras 6a y 6b. En la primer figura se presenta la mejor aproximación de la ecuación de Boussinesq a la ecuación de Richards en cuanto a la evolución de la superficie libre a la mitad de separación entre drenes (R² = 0.9761), obtenida con un valor de conductividad hidráulica a saturación para el modelo de Boussinesq de K_s = 0.500 m/h; este valor es más del doble del valor determinado en laboratorio (K_s = 0.183 m/h), con lo cual se muestra que las hipótesis consideradas en la derivación de la ecuación de Boussinesq afectan de forma sensible su capacidad de estimación de K_s. La sobrestimación del valor de K_s se traduce necesariamente en una sobrestimación de la evolución de la lámina drenada, como se muestra en la figura 6b.

Para el caso del cálculo de separación entre drenes, se obtuvo que la mejor aproximación entre el abatimiento descrito con el modelo basado en la ecuación de Boussinesq (ecuaciones (12) a (17)) y el descrito en la ecuación de Richards (ecuaciones (1) a (11)), se tiene cuando la separación entre drenes para el primer modelo es 0.40 m (R² = 0.9899). La diferencia entre la separación real del sistema de drenaje experimental considerado en el modelo de Richards (L = 1.0 m) y la separación teórica requerida con el modelo de Boussinesq para reproducir el abatimiento fijado es 153%.

 

Conclusiones

Haciendo uso de información experimental de drenaje obtenida en laboratorio para el caso de un acuífero libre con recarga vertical nula, se ha evaluado la capacidad de descripción de dos modelos mecanicistas para simular las transferencias de masa y energía en sistemas de drenaje agrícola subterráneo, uno basado en la ecuación de Richards bidimensional y otro en la ecuación de Boussinesq del drenaje agrícola. Se ha determinado que con la ecuación de Boussinesq no se pueden reproducir de manera simultánea las transferencias de masa y energía que proporciona la ecuación de Richards; por una parte, si el modelo de Boussinesq se usa para reproducir la evolución de la masa descrita con el modelo de Richards, necesariamente la ecuación de Boussinesq describe una evolución de la energía más lenta que la proporcionada por la ecuación de Richards; por otra parte, si se reproduce con el modelo de Boussinesq la variación de la energía descrita con el modelo de Richards, la ecuación de Boussinesq sobrepredice la evolución de la masa descrita por la ecuación de Richards.

Los límites de la ecuación de Boussinesq se traducen en una sobrestimación de la conductividad hidráulica a saturación cuando esta ecuación diferencial es considerada en la caracterización hidrodinámica de suelos, o bien en separación entre drenes menores de lo realmente necesario si la conductividad hidráulica a saturación es una dato estimado a partir de la ecuación de Richards.

Habida cuenta de las ventajas y el amplio uso de la ecuación de Boussinesq en el estudio del drenaje agrícola, y conocidos sus límites de descripción, se recomienda que la estimación de la conductividad hidráulica a saturación con esta ecuación diferencial se realice considerando de forma simultánea en la optimización de los parámetros K_s y ψ_d, la evolución de la lámina drenada y el abatimiento del manto freático, para distribuir proporcionalmente en éstos el efecto de las hipótesis consideradas en la derivación de la ecuación de Boussinesq y obtener adecuadas descripciones simultáneas de masa y energía. Además, el diseño de un sistema de drenaje debe ser consistente; si se estima K_s con la ecuación de Richards, debe estimarse la separación entre drenes con esta misma ecuación diferencial, y si se estima K_s con la ecuación Boussinesq, el cálculo de la separación entre drenes debe ser realizado con la ecuación de Boussinesq.

Los dos modelos presentados tienen un enfoque determinista y se aplicaron para reproducir datos obtenidos bajo condiciones bien establecidas en laboratorio. Sin embargo, ambos modelos también pueden ser aplicados al diseño y análisis de sistemas de drenaje parcelarios instalados en el campo, donde una fuerte variabilidad espacial de las propiedades hidrodinámicas del suelo puede estar presente; en este escenario, la parte esencial antes de aplicar los modelos es realizar una caracterización hidrodinámica adecuada del medio, ya sea mediante métodos directos o inversos, que permitan la determinación de parámetros globales o efectivos que satisfagan las hipótesis de los modelos presentados.

 

Agradecimientos

El trabajo fue apoyado por el Fondo de Educación Básica SEP-Conacyt, a través del proyecto SEP-2011-C01-167107.

 

Referencias

BEAR, J. Dynamics of Fluids in Porous Media. New York: Dover Publications, Inc., 1972, 764 pp.         [ Links ]

BROOKS, R.H. and COREY, A.T. Hydraulic properties of porous media. Hydrol. Pap. 3. Forth Collins: Colorado State University, 1964.         [ Links ]

BUCKINGHAM, E. Studies on the movement of soil moisture. Bureau of Soils Bulletin. No. 38, USDA, 1907, pp. 1-61.         [ Links ]

BURDINE, N.T. Relative permeability calculation from size distribution data. Pet. Trans. AIME. Vol. 198, 1953, pp. 71-78.         [ Links ]

DUMM, L.D. Drain spacing formula. Agric. Eng. Vol. 35, 1954, pp. 726-730.         [ Links ]

FIPPS, G. and SKAGGS, R.W. Drains as a Boundary Condition in Finite Elements. Water Resources Res. Vol. 22, No. 11, 1986, pp. 1613-1621.         [ Links ]

FUENTES, C., HAVERKAMP, R., and PARLANGE, J.-Y. Parameter constraints on closed-form soil-water relationships. Journal of Hydrology. Vol. 134, 1992, pp. 117-142.         [ Links ]

FUENTES, C., DE LEÓN, B., SAUCEDO, H., PARLANGE, J.-Y. y ANTONINO, A.C.D. El sistema de ecuaciones de Saint-Venant y Richards del riego por gravedad: 1. La ley potencial de resistencia hidráulica. Ingeniería Hidráulica en México. Vol. XIX, núm. 2, 2004, pp. 65-75.         [ Links ]

FUENTES, C., ZAVALA, M., and SAUCEDO, H. Relationship between the Storage Coefficient and the Soil-Water Retention Curve in Subsurface Agricultural Drainage Systems: Water Table Drawdown. J. Irrig. Drain. Eng. ASCE, Vol. 135, No. 3, 2009, pp. 279-285.         [ Links ]

GUPTA, R.K., BHATTACHARYA, A.K., and CHANDRA, P. Unsteady drainage with variable drainage porosity. Journal of Irrigation and Drainage Engineering. Vol. 120, No. 4, 1994, pp. 703-715.         [ Links ]

HAVERKAMP, R., LEIJ, F.J., FUENTES, C., SCIORTINO, A., and ROSS, P.J. Soil water retention: I. Introduction of a shape Index. Soil Sci. Soc. Am. J. Vol. 69, 2005, pp. 1881-1890.         [ Links ]

HILBERTS, A.G.J., TROCH, P.A., and PANICONI, C. Storage-dependent drainable porosity for complex hill slopes. Water Resour. Res. Vol. 41, W06001, doi: 10.1029/2004WR003725, 2005, pp. 1-13.         [ Links ]

PANDEY, R., BHATTACHARYA, A., SINGH, O., and GUPTA, S. Drawdown solution with variable drainable porosity. Journal of Irrigation and Drainage Engineering. Vol. 118, No. 3, 1992, pp. 382-396.         [ Links ]

RICHARDS, L.A. Capillary conduction of liquids through porous mediums. Physics. Vol. 1, 1931, pp. 318-333.         [ Links ]

SAMANI, J.M.V., FATHI, P., and HOMAEE, M. Simultaneous prediction of saturated hydraulic conductivity and drainable porosity using the inverse problem technique. J. Irrig. Drain. Eng. Vol. 133, No. 2, 2007, pp. 10-115.         [ Links ]

SAUCEDO, H., FUENTES, C., ZAVALA, M. y VAUCLIN, M. Una solución de elemento finito para la transferencia de agua en un sistema de drenaje agrícola subterráneo. Ingeniería Hidráulica en México. Vol. XVII, núm. 1, 2002, pp. 93-105.         [ Links ]

VAN GENUCHTEN, M.Th. A closed-form equation for predicting the hydraulic conductivity of the unsaturated soils. Soil Sci. Soc. Amer. J. Vol. 44, 1980, pp. 892-898.         [ Links ]

ZARADNY, H. and FEDDES, R.A. Calculation of Non-Steady Flow Towards a Drain in Saturated-Unsaturated Soil by Finite Elements. Agricultural Water Management. Vol. 2, 1979, pp. 37-53.         [ Links ]

ZAVALA, M., FUENTES, C. y SAUCEDO, H. Radiación fractal en la ecuación de Boussinesq del drenaje agrícola. Ingeniería Hidráulica en México. Vol. XIX, núm. 3, 2004, pp. 103-111.         [ Links ]

ZAVALA, M., FUENTES, C. y SAUCEDO, H. Radiación no lineal en la ecuación de Richards bidimensional aplicada al drenaje agrícola subterráneo. Ingeniería Hidráulica en México. Vol. XX, núm. 4, 2005, pp. 111-119.         [ Links ]

ZAVALA, M., FUENTES, C., and SAUCEDO, H. 2007. Nonlinear radiation in the Boussinesq equation of agricultural drainage. J. Hydrol. Vol. 332, No. 3-4, pp. 374-380.         [ Links ]

ZIENKIEWICZ, O.C., TAYLOR, R.L., and ZHU, J.Z. The finite element method. Its basis & fundamental. Sixth edition. Oxford: Elsevier, 2005, 733 pp.         [ Links ]