Artículos técnicos

 

Modelo de radiación fractal para el drenaje agrícola basado en las ecuaciones de Richards y Boussinesq

 

Fractal radiation model for agricultural drainage based on the Richards and Boussinesq equations

 

Manuel Zavala
Universidad Autónoma de Zacatecas, México

 

Heber Saucedo
Instituto Mexicano de Tecnología del Agua

 

Carlos Fuentes
Universidad Autónoma de Querétaro, México

 

Dirección institucional de los autores

Dr. Manuel Zavala-Trejo

Universidad Autónoma de Zacatecas
Jardín Juárez 147, Centro Histórico
98000 Zacatecas, Zacatecas, México
Teléfono: +52 (492) 1354 512
mzavala73@yahoo.com.mx

Dr. Heber Eleazar Saucedo-Rojas

Subcoordinador de Contaminación y Drenaje Agrícola
Instituto Mexicano de Tecnología del Agua
Paseo Cuauhnáhuac 8532, colonia Progreso
62550 Jiutepec, Morelos, México
Teléfono: + 52 (777) 3293 600, extensión 443
Fax: + 52 (777) 3293 659
hsaucedo@tlaloc.imta.mx

Dr. Carlos Fuentes-Ruiz

Universidad Autónoma de Querétaro
Facultad de Ingeniería
Laboratorio de Hidráulica
Centro Universitario, Cerro de las Campanas s/n
76010 Santiago de Querétaro, Querétaro, México
TELÉFONO: +52 (442) 1921 200
FAX: +52 (442) 1921 200
cbfuentesr@gmail.com

 

Recibido: 30/11/09
Aprobado: 06/10/10

 

Resumen

Se aborda la descripción del movimiento del agua en un sistema de drenaje agrícola subterráneo con un modelo basado en el acoplamiento de las ecuaciones de Richards y de Boussinesq, con capacidad de almacenamiento variable sujeta en la frontera de los drenes a una condición de radiación fractal. El modelo se aplica para describir el funcionamiento hidráulico de un sistema de drenaje instalado en campo, el cual permite estudiar separaciones entre drenes de 40 y 25 m. La mayor parte de la caracterización hidráulica del sistema es realizada de manera independiente de los eventos de drenaje, empleando una metodología basada en la curva granulométrica y porosidad total del suelo. Las evoluciones experimentales de la lámina drenada y del abatimiento del manto freático asociadas con la separación entre drenes de 40 m permiten calibrar dos parámetros del modelo propuesto, la escala de presión que interviene en la curva de retención de humedad del suelo y el parámetro de escala de la radiación fractal. La evidencia experimental correspondiente a la separación entre drenes de 25 m permite mostrar que el parámetro de escala de la radiación fractal es independiente de la separación entre drenes y que puede suponerse proporcional a la conductividad hidráulica a saturación del suelo. Se muestra que las hipótesis clásicas del drenaje agrícola que representan de manera simplificada las transferencias desarrolladas en la zona parcialmente saturada del suelo, considerando el término de recarga de la ecuación de Boussinesq nulo o igual a la evapotranspiración, trasladan la incertidumbre de lo que pasa en esta zona a los parámetros estimados a partir de las pruebas de drenaje.

Palabras clave: zona vadosa, zona saturada, acuífero libre somero, recarga, descarga.

 

Abstract

The movement of water in an agricultural subsurface drainage system is analyzed using a model based on the coupling of the Richards equation and the Boussinesq equation, with variable storage capacity subject to the drain fractal boundary radiation condition. The model is used to describe the hydraulic operation of a drainage system installed in the field, which allows for studying drain separations of 40 m and 25 m. Most of the hydraulic characterization of the system is conducted independently of drainage tests using a methodology based on the granulometric curve and total porosity of the soil. The experimental evolutions of the drained depth and the decrease in the hydraulic head associated with a 40 m separation between drains allow for calibrating two parameters of the proposed model: the pressure scale related to the soil-water retention curve and the scale parameter of the fractal radiation. The experimental evidence corresponding to a 25 m separation between drains enables showing that the scale parameter of fractal radiation is independent of the drain separation, and that it can be assumed to be proportional to the saturated hydraulic conductivity of the soil. It is shown that the classical hypotheses regarding agricultural drainage represent, in a simplified manner, the transfers developed in the partially-saturated zone, considering the recharge term in the Boussinesq equation to be null and or equal to the evapotranspiration rate; transferring uncertainty about what happens in the zone to the parameters estimated based on drainage tests.

Keywords: vadose zone, saturated zone, shallow unconfined aquifer, recharge, discharge.

 

Introducción

El análisis detallado del flujo del agua en un sistema de drenaje agrícola subterráneo requiere considerar los procesos de transferencia desarrollados en las zonas parcialmente saturada y saturada del suelo. De estas zonas, es en la parcialmente saturada, también llamada zona vadosa, donde se desarrolla lo esencial de los procesos de infiltración, extracción de agua por las plantas, evaporación, almacenamiento y recarga de acuíferos.

La mayor parte de los modelos hidrológicos que describen el flujo del agua a través del perfil del suelo sobre-simplifican la descripción de las transferencias desarrolladas en la zona vadosa (Kumar et al., 2008); estos modelos consideran relaciones de naturaleza esencialmente empírica para determinar el volumen de agua que se infiltra en el suelo, por ejemplo, el método de capacidad de infiltración media, criterio del coeficiente de escurrimiento, criterio del Servicio de Conservación de Suelos de Estados Unidos y método de los números de escurrimiento (Chow et al., 1988). La naturaleza empírica de estos métodos origina una fuerte incertidumbre sobre la generalidad y el comportamiento de sus parámetros en condiciones distintas a las de su derivación.

En un intento por mejorar la representación de la zona no saturada, otro grupo de modelos, como por ejemplo SWAT (Arnold et al., 1998), HEC-HMS (U.S. Army Corps of Engineers, 2001) y SWMM 5.0 (Rossman, 2009), han incorporado relaciones con base teórica como las ecuaciones de Green y Ampt (1911), y Horton (1940), que describen la evolución en el tiempo de la lámina infiltrada; sin embargo, ambas relaciones consideran hipótesis que limitan su capacidad de representar los procesos desarrollados en un medio real.

La descripción detallada del flujo del agua en las zonas parcialmente saturada y saturada del suelo puede hacerse con la ecuación de Richards (1931), que resulta de la combinación del principio general de conservación de masa y de la ley de Darcy generalizada. Sin embargo, la aplicación de esta ecuación a casos tridimensionales e incluso bidimensionales exhibe fuertes problemas, uno de éstos es la cantidad de información experimental requerida para determinar los parámetros de las características hidrodinámicas del suelo (curva de retención de humedad y curva de conductividad hidráulica). Otro problema es la solución numérica de la ecuación de Richards, ya que su convergencia y estabilidad requiere una discretización espacial fina del dominio de solución, un control riguroso del paso de tiempo y procedimientos iterativos que demandan gran cantidad de cálculos para linealizar y resolver el sistema de ecuaciones; esto se traduce en tiempos de cómputo que se incrementan exponencialmente conforme aumenta el tamaño del dominio de solución.

Una manera de solventar los problemas de aplicabilidad de la ecuación de Richards en tres dimensiones consiste en utilizar la ecuación de Boussinesq de los acuíferos libres, que es resultado de integrar en la vertical la ecuación de Richards, asumiendo una distribución hidrostática de presiones (e.g. Bear, 1972). En esta ecuación, las transferencias desarrolladas en la zona parcialmente saturada del suelo son consideradas de manera simplificada a través de un coeficiente de almacenamiento.

En varios modelos de drenaje agrícola, el coeficiente de almacenamiento de la ecuación de Boussinesq se ha supuesto constante (Dumm, 1954; McDonald y Harbaugh, 1988; Upadhyaya y Chauhan, 2000); sin embargo, esta hipótesis limita sensiblemente la descripción de las transferencias desarrolladas en la zona vadosa. Otros estudios han introducido un coeficiente variable que depende de la carga hidráulica, pero consideran relaciones de naturaleza empírica (e.g. Pikul et al., 1974; Pandey et al., 1992; Gupta et al., 1994; Samani et al., 2007). Recientemente, Hilberts et al. (2005) y Fuentes et al. (2009) han mostrado que el coeficiente de almacenamiento es función de la carga hidráulica y han establecido su relación con la curva de retención de humedad.

Cuando la recarga o descarga vertical al acuífero es nula, considerar el coeficiente de almacenamiento variable permite obtener representaciones aproximadas de la dinámica del agua en un acuífero libre somero (Fuentes et al., 2009); sin embargo, cuando la recarga o descarga es variable, las transferencias que se desarrollan en la zona vadosa son más complejas y se requiere considerar la variación de la conductividad hidráulica que interviene en la ley de Darcy generalizada; esto puede ser realizado acoplando la ecuación de Richards para la zona parcialmente saturada con la ecuación de Boussinesq para la zona saturada. La solución de la ecuación de Richards proporciona la intensidad de la recarga o descarga del acuífero, que es una variable de la ecuación de Boussinesq, mientras que la solución de la ecuación de Boussinesq proporciona la evolución de la superficie libre, que define las alturas de las columnas de suelo parcialmente saturado donde se aplica la ecuación de Richards. La hipótesis en este acoplamiento es que el movimiento en la zona vadosa es esencialmente vertical, lo cual permite considerar la forma unidimensional de la ecuación de Richards, y evitar cálculos y tiempos de cómputo excesivos.

Pikul et al. (1974) desarrollaron un modelo para drenaje agrícola que acopla las ecuaciones de Richards y Boussinesq en su forma unidimensional, sin embargo consideran una relación para el coeficiente de almacenamiento empírica y difícil de determinar (Vachaud y Vauclin, 1975), y además imponen en los drenes condiciones de frontera simplificadas (tipo Dirichlet o carga hidráulica especificada). García et al. (1995) desarrollaron un modelo para describir la dinámica del agua y el transporte de solutos en medios de saturación variable, acoplando las ecuaciones de Richards unidimensional, Boussinesq y advección-dispersión; recientemente, Kumar et al. (2008) han acoplado el modelo HIDRUS1D (Simúnek et al., 2005), que resuelve la ecuación unidimensional de Richards, con el modelo MODFLOW-2000 (McDonald y Harbaugh, 1988), que resuelve la ecuación general de los acuíferos y en particular la ecuación de Boussinesq para acuíferos libres someros. Sin embargo, en ambos acoplamientos se tiene como limitante que el coeficiente de almacenamiento es considerado constante y que la condición de frontera usada en los drenes agrícolas es del tipo Dirichlet (carga hidráulica especificada) o de radiación lineal (flujo de drenaje proporcional a la diferencia de presiones en la vecindad del dren).

En relación con la descripción del flujo de drenaje, se han realizado diversos estudios sobre el efecto del tamaño, forma y distribución de las perforaciones de la pared del dren en la formación de una carga hidráulica sobre éste y en la evacuación de agua del suelo (Kirkham, 1950; Engelund, 1953; Ernst, 1962; Youngs, 1974; Skaggs, 1978). Algunos modelos de la literatura relacionan las propiedades del sistema suelo-dren con la resistencia al flujo del agua en su interfaz, y establecen relaciones lineales o polinomios de segundo grado entre el gasto drenado y la carga hidráulica (Kohler et al., 2001). Zavala et al. (2007) analizan el comportamiento del flujo de drenaje, considerando el suelo y la pared del dren como objetos fractales, y establecen que la transferencia de agua del suelo al interior del dren debe ser representada con una condición de frontera de radiación no lineal o fractal. En su análisis consideran la ecuación de Boussinesq con coeficiente de almacenamiento constante, recarga nula, y calibran los parámetros de la radiación fractal a partir de un evento de drenaje de laboratorio.

El objetivo de este trabajo es desarrollar un modelo para el drenaje agrícola subterráneo que considere las transferencias desarrolladas en la zona vadosa del suelo bajo recarga o descarga vertical variable en el tiempo, basado en el acoplamiento de la ecuación de Richards unidimensional y la ecuación de Boussinesq unidimensional con coeficiente de almacenamiento variable sujeta en los drenes a una condición de radiación fractal. Se realizará la estimación de los parámetros de la radiación fractal considerando datos obtenidos en una prueba de drenaje realizada en campo y se evaluará su capacidad de descripción considerando datos medidos en un segundo evento de drenaje.

 

Ecuaciones de base

La figura 1 muestra un esquema del flujo no saturado-saturado que se presenta en un sistema de drenaje subsuperficial; se considera un acuífero libre somero con drenes paralelos equidistantes y estrato impermeable horizontal. En esta figura se representa una columna de suelo parcialmente saturado, cuya altura varía en el tiempo y espacio, en función de las condiciones de flujo en la superficie del suelo, del flujo de agua que se evacua a través de los drenes, de las propiedades físicas e hidráulicas del medio poroso y de las características geométricas del sistema. La base de cada columna de suelo corresponde a la posición de la superficie libre de agua o nivel freático, y su altura se extiende hasta la superficie del suelo.

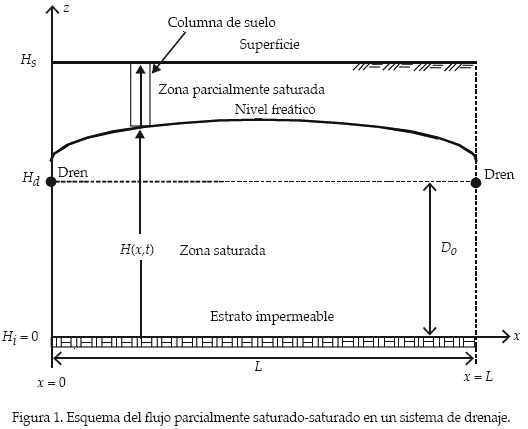
Zona parcialmente saturada (zona vadosa)

La descripción del movimiento del agua en una columna de suelo parcialmente saturado, homogéneo e isotrópico, puede realizarse con la ecuación de Richards (1931), que resulta de la combinación de la ecuación de continuidad y la ley de Darcy generalizada:

donde Ψ = Ψ(z, t) es el potencial de presión del agua en el suelo, expresado como una altura equivalente de columna de agua [L]; el potencial gravitacional ha sido asimilado a la coordenada vertical z, orientada positivamente en dirección ascendente [L]; t es el tiempo [T]; K(Ψ) es la conductividad hidráulica en función de la presión del agua en el suelo [LT^-1]; C(Ψ) = dθ(Ψ)/ dΨ es la capacidad específica [L^-1]; θ = θ(Ψ) es el contenido volumétrico de agua o contenido de humedad [L³L^-3] y depende de la presión del agua en el suelo, esta dependencia es conocida como la característica de humedad o curva de retención de humedad.

Condiciones límite

La resolución de la ecuación de Richards requiere la definición de las condiciones límite que representen el proceso que se desarrolla en la columna de suelo parcialmente saturado. Como condición inicial debe especificarse la distribución de presiones en la zona vadosa del suelo:

La base de la columna de suelo corresponde a la posición de la superficie libre de agua (potencial de presión nulo), por lo que debe imponerse una condición de frontera tipo Dirichlet homogénea:

H es la elevación de la superficie libre o nivel freático, medida desde el estrato impermeable.

En la frontera superior de la columna de suelo puede usarse una condición tipo Dirichlet si se desea representar el efecto de saturación asociado con el riego por gravedad o al generado por un escurrimiento superficial:

O bien puede usarse una condición de frontera tipo Neumann de flujo prescrito:

donde H_s es la elevación de la superficie del suelo medida desde un nivel de referencia, en este caso el estrato impermeable; y f₀ (t) es un valor de flujo conocido, como la intensidad de la evaporación o de la precipitación. La condición (4.2) también puede usarse para representar la evapotranspiración de un cultivo, sobre todo en la etapa inicial de su ciclo fenológico, cuando el desarrollo de las raíces no es profundo y la mayor parte del proceso evapotranspirativo se desarrolla en zonas del suelo cercanas a la superficie.

Propiedades hidráulicas del suelo

La resolución de la ecuación de Richards (1) sujeta a las condiciones (2-4) requiere el uso de modelos que relacionen el contenido volumétrico de agua θ con el potencial de presión del agua en el suelo Ψ, así como la conductividad hidráulica K con el contenido volumétrico de humedad θ. Fuentes et al. (1992) han analizado los modelos clásicos usados en la literatura para representar las propiedades del suelo y han demostrado que la mayor parte no satisface las propiedades integrales de la infiltración; también han determinado que una combinación de modelos que satisface estas propiedades y que es útil en estudios experimentales es el modelo para la característica de humedad de van Genuchten (1980), sujeto a la restricción de Burdine (1953):

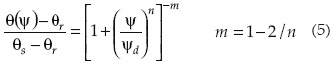
donde θ_s es el contenido volumétrico de agua a saturación [L³L^-3]; 8_r es el contenido volumétrico de agua residual [L³L^-3]; Ψ_d es un parámetro de escala de la presión [L]; m y n son parámetros de forma empíricos adimensionales.

Y el modelo para la conductividad hidráulica de Brooks y Corey (1964):

donde K_s es la conductividad hidráulica a saturación [LT^-1] y η es un parámetro forma adimensional.

Zona saturada

La dinámica del agua en un acuífero libre somero puede ser representada con la ecuación de Boussinesq del drenaje agrícola, que resulta del principio de conservación de masa, la ley de Darcy y la hipótesis de Dupuit-Forcheimer concerniente a una distribución hidrostática de presiones:

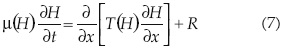
donde T = K_s(H - H_i) es la transmisibilidad del acuífero [L²T^-1]; (H -H_i) representa el espesor del acuífero [L], siendo H y H_i las elevaciones de la superficie libre o carga hidráulica y del estrato impermeable [L], medidas desde el mismo nivel de referencia; cuando el estrato impermeable es aproximadamente horizontal, se puede asumir H_i= 0; R es el volumen de recarga o descarga vertical por unidad de área de acuífero por unidad de tiempo [L³L^-2T^-1]; y μ(H) es el coeficiente de almacenamiento [L³L³], que en un acuífero libre es función de la carga hidráulica (Hilberts et al., 2005; Fuentes et al., 2009).

Coeficiente de almacenamiento

De acuerdo con Fuentes et al. (2009), el coeiciente de almacenamiento en un acuífero libre somero está relacionado con la curva de retención de humedad de la siguiente manera:

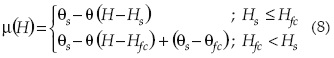
donde H_fc = H + |Ψ_fc| y Ψ_fc es el potencial de presión asociado con el concepto de capacidad de campo, en suelos de textura arenosa |Ψ_fc| ≅ 1.0 m y suelos arcillosos |Ψ_fc| ≅ 3.3 m.

La introducción de la curva de retención (ecuación (5)) en la definición del coeficiente de almacenamiento (ecuación (8)) permite obtener la siguiente relación:

Condiciones límite

De acuerdo con Zavala et al. (2007), la descripción de la dinámica del agua en sistemas de drenaje subterráneos con la ecuación (7) requiere el uso de las siguientes condiciones límite:

donde H_o(x) es la posición inicial del manto freático, que puede ser función de la coordenada horizontal x. El signo positivo en la condición de frontera (11) se toma para el dren ubicado en x = 0, mientras que el negativo para el que está ubicado en x = L, donde L es la separación entre drenes. En la ecuación (11) se introduce el flujo de drenaje (q_d) proporcionado por la radiación fractal:

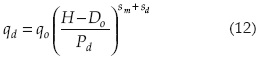
q_o es el valor máximo del flujo de drenaje; P_d es la profundidad de los drenes; D_o es la profundidad del estrato impermeable medida desde la posición de los drenes; s_m y s_d son la dimensión cociente del suelo y de la pared del dren (razón entre la dimensión fractal del objeto D_f y la dimensión del espacio de Euclides). La dimensión cociente de un objeto fractal (s) está relacionada con su porosidad volumétrica (Φ) de acuerdo con:

y considerando que la porosidad areal es Φ = φ^2s, se obtiene:

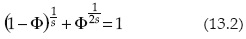
En las ecuaciones (13.1) y (13.2) se introduce s_m y s_d en lugar de s para calcular las dimensiones del suelo y de la pared del dren, respectivamente.

El gasto total evacuado por cada dren es proporcionado por la relación:

donde ℒ es la longitud del dren.

 

Solución numérica

Los sistemas de ecuaciones (1-6) y (7-14) se resuelven numéricamente de la siguiente manera: la discretización espacial se realiza con el método del elemento finito tipo Galerkin (Zienkiewicz et al., 2005); la discretización temporal se hace aplicando un método de diferencias finitas (Herbert y Anderson, 1995); los sistemas resultantes de la discretización se linealizan empleando el procedimiento iterativo de Picard, mientras que los sistemas de ecuaciones algebraicas se resuelven usando el método de gradiente conjugado precondicionado propuesto por Noor y Peters (1987).

El esquema numérico para la ecuación de Richards es:

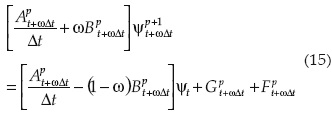
donde t es el tiempo; Δt es el paso de tiempo; w es un coeficiente de ponderación en el tiempo (0 < ω < 1); p indica el número de iteración en el intervalo de tiempo; A es la matriz de masa; B es la matriz de rigidez; G es el vector de la fuerza de gravedad; F es el vector de flujos en la frontera (z = H_s); ψ es el vector que contiene los valores del potencial de presión en los nodos del elemento finito. El uso de funciones de interpolación lineales y funciones del sistema de masa concentrado (Zienkiewicz et al., 2005) permite obtener los coeficientes siguientes:

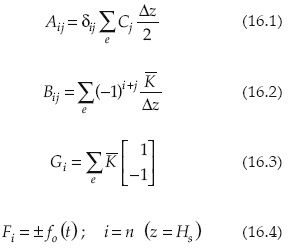
n es el número de nudos considerados en la discretización de la columna de suelo; e = n -1 es el número total de elementos finitos; i y j son índices para referenciar el número de nudo de cada elemento (1, 2,..., n), el primer índice está asociado con la solución aproximada de elemento finito, mientras que el segundo índice está relacionado con las funciones de peso que se utilizan para minimizar el error de la discretización espacial (Zienkiewicz et al., 2005); δ_ij es la delta de Kronecker; C es la capacidad específica en los nudos del elemento; Δz es el tamaño del elemento finito; 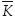es la conductividad hidráulica en el elemento, tomada como el promedio aritmético de las conductividades en los nudos del elemento; f₀(t) es la evolución del flujo de Darcy en la superficie del suelo; el signo positivo se toma cuando se representa la intensidad de la precipitación y el signo negativo cuando se representa la evaporación o evapotranspiración en función del tiempo.

El esquema numérico para la ecuación de Boussinesq es el siguiente:

donde H es el vector que contiene los valores de la carga hidráulica. En este caso, los coeficientes de la matriz de masa M, matriz de rigidez B, vector de flujos en la frontera F y vector de recarga o descarga R_c son:

N es el número de nudos considerados en la discretización del dominio de solución definido a partir de la separación entre drenes L; i y j son índices para referenciar el número de nudo del elemento finito (1, 2,..., N), el primer índice está asociado con la solución de elemento finito, mientras que el segundo índice está relacionado con las funciones de peso que se utilizan para minimizar el error de la discretización espacial; e = N - 1 es el número de elementos finitos: Δx es el tamaño del elemento; es el coeficiente de almacenamiento en los nudos del elemento; T es la transmisibilidad en el elemento, tomada como el promedio aritmético de las transmisibilidades en los nudos del elemento finito; q_d es el flujo de drenaje calculado con la radiación fractal (ecuación (12)); y R es la intensidad de la recarga o descarga del acuífero, que es igual a la magnitud del flujo de Darcy sobre la base de la columna de suelo parcialmente saturado q(z = H,t) = -K(Ψ)[(∂Ψ/∂z) + 1].

Acoplamiento numérico

a) En el intervalo de tiempo Δt se resuelve primeramente el sistema asociado con la ecuación de Boussinesq, considerando un valor de recarga o descarga (R): cero si es el tiempo inicial (t = Δt) y la primera iteración (p = 1); el valor calculado en el tiempo anterior si t > Δt y p = 1; o el valor obtenido en la iteración previa si p > 1. Con este procedimiento se obtiene la posición de la superficie libre en el intervalo de tiempo.

b) A partir de la posición del manto freático H(x,t) se definen las alturas de las columnas de suelo parcialmente saturado y se resuelve el sistema asociado con la ecuación de Richards en cada una de estas columnas, obteniéndose la distribución de presiones y la magnitud del flujo de Darcy en la base de las columnas.

Los pasos a y b se repiten en el intervalo de tiempo Δt hasta satisfacer el criterio de convergencia seleccionado (tolerancia para el máximo cambio tanto de la posición de la superficie libre como del flujo de Darcy en la base de las columnas de suelo entre iteraciones consecutivas); en este proceso iterativo se ajusta continuamente la altura de las columnas de suelo parcialmente saturado en función de la posición de la superficie libre.

 

Aplicación

El modelo Richards-Boussinesq se aplica para caracterizar y describir el funcionamiento del sistema de drenaje subterráneo de una parcela agrícola localizada en el municipio de Sinaloa de Leyva, Sinaloa, México, perteneciente al distrito de riego 075 Río Fuerte. La parcela tiene una superficie de 8.4 ha y cuenta con seis líneas paralelas de drenes subterráneos de polietileno corrugado de 10 cm de diámetro, instaladas a una profundidad media P_d = 1.20 m, que descargan libremente a un dren colector superficial; tres de las líneas presentan una separación entre drenes L₁ = 40 m y drenan el 68% de la superficie total, mientras que las tres restantes tienen una separación entre drenes L₂ = 25 m y cubren el 32% de la parcela. La pared de los drenes tiene entre cada corrugación seis perforaciones distribuidas a la largo de su perímetro (cada 60°); el área perforada por metro de dren es de 32 cm², por lo que la porosidad areal de la pared es Φ_d = 0.0102 cm²/cm².

Para obtener información experimental que permita aplicar el modelo numérico, se monitoreó el funcionamiento de las líneas de drenaje centrales asociadas con cada separación entre drenes, lo cual elimina las perturbaciones originadas por el cambio de separación. Utilizando el plano de la parcela experimental, se delimitó el área de influencia de cada una de las líneas de drenaje seleccionadas, se dividió cada zona en tres secciones y en cada celda se seleccionó un punto de muestreo de suelo, considerando tres profundidades: 0-35 cm, 35-70 cm y 70-130 cm. En el perfil de suelo se detectó un estrato de suelo prácticamente impermeable a 4.20 m de profundidad, por lo que D_o = 3.0 m.

Las muestras de suelo, nueve por cada línea de drenaje, se analizaron en laboratorio para determinar la porosidad, granulometría y textura; los resultados obtenidos muestran que se tiene poca variabilidad espacial de estas propiedades físicas en cada una de las zonas analizadas (cuadro 1). En consecuencia, se justifica considerar en la modelación la hipótesis de suelo homogéneo para cada zona de suelo.

Previo a la evaluación hidráulica del sistema de drenaje se realizaron las siguientes actividades: rastreo, trazo de regaderas y colectores superficiales, siembra en seco, trazo de surcos a 0.80 m de separación y construcción de pozos de observación del manto freático a la mitad de separación entre drenes. Posteriormente se taparon las descargas de las seis líneas de drenaje y se aplicó el riego superficial de germinación hasta saturar completamente el suelo. Concluida la aplicación del riego se mantuvieron cerradas las descargas de las líneas de drenaje durante doce horas para permitir una mejor distribución del agua y de la presión en el suelo. Finalmente se destaparon las seis líneas de drenaje y se midió durante 15 días el volumen de agua evacuado a través de los drenes centrales asociados con la separaciones de 40 y 25 m; de manera simultánea se midió la evolución del manto freático a la mitad de separación entre drenes.

La evolución en el tiempo de la evapotranspiración de referencia (Et_o) en el periodo del experimento se tomó de los registros de la estación climatológica automática Batequis, localizada a 6 km de la parcela experimental. Esta información sirvió de base para estimar la evapotranspiración del trigo sembrado en la parcela experimental (Et_c); el valor del coeficiente de cultivo considerado en la estimación K_o = 0.40 corresponde a la etapa inicial del trigo. En la figura 2 se muestra la variación en el tiempo de la evapotranspiración de referencia y la evapotranspiración del trigo.

Caso 1. Separación entre drenes de 40 m

Se aborda la descripción de los procesos de transferencia desarrollados en la zona de suelo dominada por la línea de drenaje central de la separación entre drenes L₁ = 40 m. La longitud total de este dren es ℓ = 446.20 m y su pendiente longitudinal es S₀ = 0.12%.

La modelación del evento de drenaje requiere la determinación de los parámetros que intervienen en la curva de retención de humedad (ecuación (5)), curva de conductividad hidráulica (ecuación (6)), coeficiente de almacenamiento variable (9) y condición de radiación fractal (12). Es esencial minimizar el número de parámetros a determinar a partir del evento transitorio de drenaje monitoreado, ya que entre mayor es la cantidad de parámetros que se estimen de una sola prueba, se gana en cuanto a la descripción de la experiencia particular, pero se pierde en cuanto al sentido de generalidad y capacidad de explicación del porqué y del cómo de los procesos. En consecuencia, la caracterización hidrodinámica se realiza aplicando la metodología recomendada por Fuentes (1992), basada en la curva granulométrica y porosidad total del suelo.

El contenido volumétrico de agua a saturación θ_s se asimila a la porosidad total del suelo Φ. De acuerdo con los datos del cuadro 1 se tiene una porosidad promedio para esta zona de suelo de Φ = 0.469 cm³/cm³, en consecuencia, θ_s = 0.469 cm³/cm³. De acuerdo con Haverkamp et al. (2005), para reducir los parámetros de ajuste, el contenido volumétrico de agua residual puede asumirse igual a cero (θ_r = 0 cm³/cm³), lo cual implica aceptar que cuando Ψ → -∞ necesariamente θ → 0.

El parámetro m de las relaciones (5) y (9), así como el parámetro η de la relación (6), se estiman a partir de la curva granulométrica del suelo y de su porosidad total. De acuerdo con el modelo funcional de la curva de retención (5), se ajusta la curva granulométrica del suelo con la función de distribución:

donde F(D) es la frecuencia acumulada basada en el peso de las partículas, cuyos diámetros son inferiores o iguales a D; D_G es un tamaño característico de las partículas; M y N son dos parámetros de forma empíricos, que de acuerdo con la restricción de Burdine (1953) se relacionan como M = 1 - 2/N, con 0 < M < 1 y N > 2. El mejor ajuste de la ecuación (19) con la curva granulométrica representativa de la zona en análisis (R² = 0.9975) se obtiene con D_g = 280 μm y M = 0.084 (figura 3).

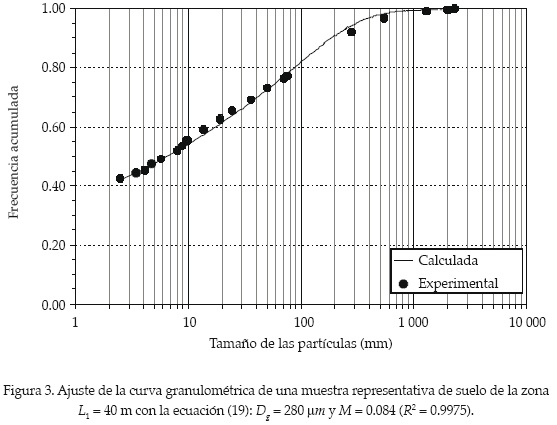
Haciendo λ = mn y m_u = MN, el parámetro de forma m de la curva de retención de van Genuchten puede relacionarse con M a través de la fórmula m_u/λ = 1 + (2s_m - 1)/2(1 - s_m). Introduciendo el valor de la porosidad volumétrica del suelo en la ecuación (13.1) se tiene s_m = 0.688, y con el valor de m_u = MN = 0.183 se deduce λ = mn = 0.115, de donde m = 0.054. La potencia de la curva de conductividad hidráulica se calcula con la relación η = 2s_m (1 + 2/λ), obteniéndose η = 25.4.

La conductividad hidráulica a saturación (K_s) se determinó en laboratorio mediante una prueba de carga de agua constante aplicada en una columna de suelo saturado; el valor obtenido es K_s = 0.060 m/d. La porosidad volumétrica de la pared del dren se determina introduciendo su valor de porosidad areal en la relación (13.2) y resolviendo esta función implícita, obteniéndose s_d = 0.569.

Los parámetros que completan la caracterización del sistema de drenaje son Ψ_d (ecuación (5)) y q_o (ecuación (12)), y se determinan a partir de la evolución de la lámina drenada experimental y la evolución del abatimiento del manto freático medida a la mitad de separación entre drenes. El procedimiento consiste en aplicar el modelo numérico Richards-Boussinesq (ecuaciones (15) a (18)) y determinar la combinación de valores que minimiza la diferencia entre datos medidos y calculados. En la modelación, la evapotranspiración se representa de manera simpliicada, imponiendo en la frontera superior de las columnas de suelo parcialmente saturado (supericie del suelo), una condición de frontera tipo Neumann variable en el tiempo (ecuación (4.2)), cuyos valores corresponden a la evapotranspiración del trigo estimada previamente (Et_c en la igura 2). La condición inicial de la simulación corresponde a la observada en el experimento, H(x,0) = H_s.

La combinación de valores que minimiza la diferencia entre las evoluciones de la lámina drenada y la supericie libre, experimental y calculada, es Ψ_d = -0.70 m y q_o = 27.5 K, siendo el error cuadrático medio RECM = 1.62 × 10^-4 m y RECM = 4.02 x 10^-4 m, respectivamente. En las iguras 4a y 4b se muestran los resultados obtenidos. La correspondencia entre datos medidos y observados es satisfactoria.

Para mostrar la importancia de la zona vadosa en el funcionamiento de un sistema de drenaje, se comparan los resultados del modelo Richards-Boussinesq contra los resultados del modelo basado sólo en la ecuación de Boussinesq con coeiciente de almacenamiento variable; se consideran los parámetros del suelo y de la radiación fractal obtenidos precedentemente, así como la condición de carga hidráulica observada al inicio del experimento. Se analizan dos escenarios clásicos considerados en la literatura cuando se modela con la ecuación de Boussinesq; el primero consiste en asumir que la descarga del acuífero somero por efecto de la evapotranspiración es nula (R = 0), y el segundo consiste en aceptar que la evapotranspiración del cultivo tiene un efecto instantáneo sobre el manto freático, sin importar las condiciones de humedad, capacidad de retención y flujo en la zona vadosa, es decir R = -Et_c(t). Los resultados de las modelaciones numéricas se muestran en las figuras 5a y 5b (4), donde se observa que el modelo basado en la ecuación de Boussinesq con la hipótesis de descarga nula sobre-predice la evolución la lámina de agua drenada y subestima el abatimiento del manto freático; mientras que con el supuesto de descarga igual a la evapotranspiración variable en el tiempo se subestima sensiblemente la evolución de la lámina drenada y se sobreestima el abatimiento del nivel freático. Estos resultados permiten mostrar que cuando se realiza la estimación de parámetros de un sistema de drenaje exclusivamente con la ecuación de Boussinesq, los valores que se obtienen en la calibración absorben la sobre-simplificación de los procesos de transferencia desarrollados en la zona parcialmente saturada del suelo; en este caso, los parámetros Ψ_d y q_o hubiesen tenido un valor diferente al determinado con el modelo Richards-Boussinesq.

Caso 2. Separación entre drenes de 25 m

La segunda configuración del sistema de drenaje experimental, L₂ = 25 m, es analizada con el modelo Richards-Boussinesq. La línea evaluada tiene una longitud de 353.50 m y una pendiente de 0.12%; la profundidad del estrato impermeable medida desde los drenes es D_o = 3.0 m, y la variación en el tiempo de la evapotranspiración usada como condición de frontera superior de las columnas de suelo no saturadas es la que se muestra en la figura 2.

La caracterización hidrodinámica del suelo se realiza con el procedimiento descrito previamente. Los resultados obtenidos son Φ = 0.474 cm³/cm³, θ_s = 0.474 cm³/cm³, θ_r = 0.0 cm³/cm³, m = 0.043, η = 32.25 y K_s = 0.082 m/d. Mientras que los parámetros de forma de la radiación fractal son s_m = 0.691, s_d = 0.569. Se retiene con fines de validación el parámetro de escala de la condición de radiación fractal previamente estimado (q_d = 27.5 K_s).

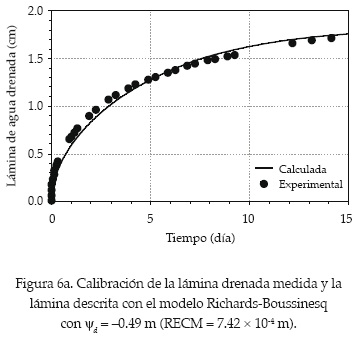
En esta modelación, el único parámetro de calibración es y_d, el cual se determina a partir de la evolución de la lámina drenada experimental. El valor que minimiza la diferencia entre la lámina experimental medida y la lámina calculada con el modelo Richards-Boussinesq es Ψ_d = -0.49 m (figura 6a), siendo la suma del error cuadrático medio RECM = 7.42 × 10^-4 m. Los resultados presentados en la figura 6b muestran que la descripción del abatimiento del nivel freático obtenida con el modelo Richards-Boussinesq describe aceptablemente la evolución experimental (RECM = 5.09 × 10^-4 m), sobre todo si se considera que la evolución medida no es elemento de calibración sino de validación; esta evidencia muestra que para el intervalo de separación entre drenes considerado en este trabajo (25 m < L < 40 m), el parámetro de escala de la radiación fractal q_o no exhibe una dependencia aparente de la separación entre drenes y puede ser relacionado con el valor de K_s.

 

Conclusiones

Los procesos de transferencia desarrollados en la zona parcialmente saturada del suelo o zona vadosa son de fundamental importancia para definir la dinámica del agua en el espesor saturado del suelo. En el caso de los sistemas de drenaje agrícola subterráneo, donde el abatimiento y/o control del manto freático somero es fundamental, es necesario representar estos procesos de manera explícita en los modelos matemáticos que describen su funcionamiento hidráulico.

A fin de considerar los procesos desarrollados en la zona no saturada del suelo en el análisis del drenaje agrícola subterráneo, se ha desarrollado un modelo de simulación basado en el acoplamiento numérico de las ecuaciones de Richards y de Boussinesq con capacidad de almacenamiento variable sujeta en los drenes a una condición de radiación fractal. Se ha implementado un algoritmo iterativo para la convergencia del acoplamiento Richards-Boussinesq, en el que se calcula y ajusta sistemáticamente la posición de la superficie libre, la altura de las columnas de suelo parcialmente saturado y la magnitud del flujo de Darcy en la base de estas columnas.

El modelo desarrollado ha sido aplicado para caracterizar y describir el funcionamiento hidráulico del sistema de drenaje subterráneo de una parcela agrícola experimental del distrito de riego 075 Río Fuerte, Sinaloa; los drenes en esta parcela están instalados a una profundidad media de 1.20 m y presentan separaciones de 40 y 25 m, siendo el suelo de textura esencialmente arcillosa. Se hicieron dos pruebas de drenaje para determinar los parámetros del modelo y validar parcialmente sus resultados.

Los parámetros de forma de las características hidrodinámicas del suelo y de la condición de radiación fractal usada en los drenes se han estimado empleando una metodología basada en la curva granulométrica y porosidad total del suelo. A partir de los datos de la prueba de drenaje asociada con la separación entre drenes L₁ = 40 m, se han determinado los valores de los parámetros de escala que intervienen en la curva de retención de humedad del suelo y en la condición de radiación fractal; el procedimiento consistió en minimizar el error entre las evoluciones medidas de la lámina drenada y la superficie libre, y las evoluciones calculadas con el modelo Richards-Boussinesq. La no presencia de oscilaciones e inestabilidades en las evoluciones de lámina drenada y de la superficie libre descritas con el modelo es un indicador de la consistencia del método numérico empleado para resolver el acoplamiento Richards-Boussinesq.

La modelación de la prueba de drenaje para la separación entre drenes L₂ = 25 m ha permitido mostrar que el parámetro de escala de la radiación fractal no depende de la separación entre drenes. En consecuencia, si se tienen drenes instalados a 1.20 m de profundidad en un suelo de textura arcillosa, este parámetro puede considerarse proporcional a la conductividad hidráulica a saturación del suelo.

Se ha mostrado que cuando las transferencias desarrolladas en la zona vadosa del suelo se representan de manera simplificada, considerando exclusivamente la ecuación de Boussinesq con recarga nula o igual a la evapotranspiración variando en el tiempo, se traslada la incertidumbre de lo desarrollado en esta zona al valor de los parámetros que se estimen a partir de las pruebas de drenaje. Este problema puede ser minimizado con el modelo Richards-Boussinesq propuesto en este trabajo.

 

Referencias

ARNOLD, J.G., SRINIVASAN, R., MUTTIAH, R.S., and WILLIAMS, J.R. Large area hydrologie modeling and assessment. Part 1: Model development. J. Am. Water Res. Assoc. Vol. 34, No. 1, 1998, pp. 73-89.         [ Links ]

BEAR, J. Dynamics of Fluids in Porous Media. New York: Dover Publications, Inc., 1972, 764 pp.         [ Links ]

BROOKS, R.H. and COREY, A.T. Hydraulic properties of porous media. Hydrol. Pap. 3. Fort Collins: Colorado State University, 1964.         [ Links ]

BURDINE, N.T. Relative permeability calculation from size distribution data. Pet. Trans. AIME. Vol. 198, 1953, pp. 71-78.         [ Links ]

CHOW, V.T., MAIDMENT, D.R., and MAYS, L.W. Applied Hydrology. New Edition (First edition). New York: McGraw-Hill Companies, 1988, 572 pp.         [ Links ]

DUMM, L.D. Drain spacing formula. Agricultural Engineering. Vol. 35, 1954, pp. 726-730.         [ Links ]

ENGELUND, F. On the laminar and turbulent flows of ground water through homogeneous sand. Trans. Danish Acad. Technnol. Sci. ATS 3, 1953, pp. 1-105.         [ Links ]

ERNST, L.F. Grondwaterstromingen in de verzadigde zone en hun berekening bij de aanwezigheid van horizontale evenwijdige open leidingen. Wageningen, The Netherlands: Verslagen Landbouwkundig Onderzoek, Pudoc., 1962, 67 pp.         [ Links ]

FUENTES, C. Approche fractale des transferts hydriques dans les sols non saturés. Tesis de Doctorado. Grenoble: Universidad Joseph Fourier de Grenoble, 1992, 267 pp.         [ Links ]

FUENTES, C., HAVERKAMP, R., and PARLANGE, J.-Y. Parameter constraints on closed-form soil-water relationships. J. Hydrol. Vol. 134, 1992, pp. 117-142.         [ Links ]

FUENTES, C., ZAVALA, M., and SAUCEDO, H. Relationship between the Storage Coefficient and the Soil-Water Retention Curve in Subsurface Agricultural Drainage Systems: Water Table Drawdown. J. Irrig. Drain. Eng. ASCE. Vol. 135. No. 3, 2009, pp. 279-285.         [ Links ]

GARCÎA, L.A., MANGUERRA, H.B., and GATES, T.K. Irrigation-drainage design and management model: development. J. Irrig. Drain. Eng. ASCE. Vol. 121, No. 1, 1995, pp. 71-82.         [ Links ]

GREEN, W.H. and AMPT, G.A. Studies in the soils physics 1: the flow of air and water through soils. J. Agric. Sci. Vol. 4, 1911, pp. 1-24.         [ Links ]

GUPTA, R.K., BHATTACHARYA, A.K., and CHANDRA, P. Unsteady drainage with variable drainage porosity. J. Irrig. Drain. Eng. Vol. 120, No. 4, 1994, pp. 703-715.         [ Links ]

HAVERKAMP, R., LEIJ, F.J., FUENTES, C., SCIORTINO, A., and ROSS, P.J. Soil water retention: I. Introduction of a shape Index. Soil Sci. Soc. Am. J. Vol. 69, 2005, pp. 1881-1890.         [ Links ]

HERBERT, F.W. and ANDERSON, M.P. Introduction to Groundwater Modeling: Finite Difference and Finite Element Methods. London: Academic Press, 1995, 237 pp.         [ Links ]

HILBERTS, A.G.J., TROCH, P.A., and PANICONI, C. Storage-dependent drainable porosity for complex hillslopes. Water Resour. Res. Vol. 41, W06001, doi:10.1029/2004WR003725, 2005, pp. 1-13.         [ Links ]

HORTON, R.E. An approach toward a physical interpretation of infiltration capacity. Soil Science Society of America Proceedings. Vol. 5, 1940, pp. 399-417.         [ Links ]

KIRKHAM, D. Potential flow into circumferential openings in drains. Trans. Am. Geophys. Union. Vol. 39, 1950, pp. 892-908.         [ Links ]

KOHLER, A., ABBASPOUR, K.C., FRITSCH, M., VAN GENUCHTEN, M.TH., and SCHULIN, R. Simulating unsaturated flow and transport in a macroporous soil to tile drains subject to an entrance head: model development and preliminary evaluation. Journal of Hydrology. Vol. 254, 2001, pp. 67-81.         [ Links ]

KUMAR, N., TWARAKAVI, C., SIMUNEK, J., and SEO, S. Evaluating Interactions between Groundwater and Vadose Zone Using the HYDRUS-Based Flow Package for MODFLOW. Vadoze Zone Journal. Vol. 7, No. 2, 2008, pp. 757-768.         [ Links ]

MCDONALD, M.G. and HARBAUGH, A.W. A modular three-dimensional finite-difference ground-water flow model: U.S. Geological Survey Techniques of Water-Resources Investigations. Book 6, chap. A1, Denver, 1988, 586 pp.         [ Links ]

NOOR, A. and PETERS, J.M. Preconditioned conjugate gradient technique for the analysis of symmetric structures. Int. J. Numer. Meth. Eng. Vol. 24, 1987, pp. 2057-2070.         [ Links ]

PANDEY, R.S., BHATTACHARYA, A.K., SINGH, O.P., and GUPTA, S.K. Drawdown solution with variable drainable porosity. J. Irrig. Drain. Eng. Vol. 118, No. 3, 1992, pp. 382-396.         [ Links ]

PIKUL, M.F., STREET, R.L., and REMSON, I. A numerical model based on coupled one-dimensional Richards and Boussinesq equations. Water Resour. Res. Vol. 10, No. 2, 1974, pp. 295-301.         [ Links ]

RICHARDS, L.A. Capillary conduction of liquids through porous mediums. Physics 1. 1931, pp. 318-333.         [ Links ]

ROSSMAN, L.A. Storm Water Management Model, Version 5.0: User's Manual. Cincinnati: Water Supply and Water Resources Division, National Risk Management Research Laboratory Cincinnati, OH 45268 National, 2009, 266 pp.         [ Links ]

SAMANI, J.M.V., FATHI, P., and HOMAEE, M. Simultaneous Prediction of Saturated Hydraulic Conductivity and Drainable Porosity Using the Inverse Problem Technique. J. Irrig. Drain. Eng. Vol. 133, No. 2, 2007, pp. 110-115.         [ Links ]

ŠIMŮNEK, J., VAN GENUCHTEN, M.TH., and SEJNA, M. The HYDRUS-1D software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media, Version 3.0. HYDRUS Softw. Ser. 1. Riverside: Dep. of Environ., Sci., Univ. of California, 2005.         [ Links ]

SKAGGS, R.W. Effect of drain tube openings on water table drawdown. ASCE. Journal of Irrigation and Drainage Division. Vol. 104, IR1, 1978, pp. 13-21.         [ Links ]

UPADHYAYA, A. and CHAUHAN, H.S. An analytical solution for bi-level drainage design in the presence of evapotranspiration. Agric. Water Man. Vol. 45, 2000, pp. 169-184.         [ Links ]

U.S. ARMY CORPS OF ENGINEERS. Hydrologic Engineering Center, Hydrologic Modeling System. Version 2.1: User's Manual. Davis: Hydrologic Engineering Center, 609 Second Street Center, Davis, CA 95616-4687, USA, 2001, 178 pp.         [ Links ]

VACHAUD, G. and VAUCLIN, M. Comments on 'A numerical model based on coupled one-dimensional Richards and Boussinesq equations' by M.F. Pikul, R.L. Street y I. Remson. Water Resour. Res. Vol. 11, No. 3, 1975, pp. 506-509.         [ Links ]

VAN GENUCHTEN, M.Th. A closed-form equation for predicting the hydraulic conductivity of the unsaturated soils. Soil Sci. Soc. Amer. J. Vol. 44, 1980, pp. 892-898.         [ Links ]

YOUNGS, E.G. Water-table heights in homogeneous soils drained by non ideal drains. Soil Sci. Vol. 117, 1974, pp. 295-300.         [ Links ]

ZAVALA, M., FUENTES, C., and SAUCEDO, H. Nonlinear radiation in the Boussinesq equation of agricultural drainage. J. of Hydrol. Vol. 332, No. 3, 2007, pp. 374-380.         [ Links ]

ZIENKIEWICZ, O.C., TAYLOR, R.L., and ZHU, J.Z. The Finite Element Method. Its Basis and Fundamental. Sixth ed. Amsterdam: Elsevier, 2005, 733 pp.         [ Links ]