Nota técnica

 

Solución numérica de flujo con potencial en geometrías complejas

 

Numerical solution of potential flow in complex geometries

 

Alejandro Mendoza-Reséndiz y Moisés Berezowsky-Verduzco

 

Universidad Nacional Autónoma de México.

 

Dirección institucional de los autores

M.I. Alejandro Mendoza-Reséndiz
Dr. Moisés Berezowsky-Verduzco

Universidad Nacional Autónoma de México
Instituto de Ingeniería
Coordinación de Hidráulica
Edificio 5, Circuito Escolar, Ciudad Universitaria
Delegación Coyoacán
04510 México, D.F., México
Teléfono +52 (55) 5623 3600, extensión 8644
amendozar@iingen.unam.mx
mbv@pumas.iingen.unam.mx

 

Recibido: 06/04/09
Aprobado: 01/09/10

 

Resumen

Se presenta una metodología para calcular de forma numérica el flujo con potencial, empleando mallas curvilíneas compuestas. Las mallas curvilíneas tienen la ventaja de adaptarse a las formas irregulares del dominio físico; sin embargo, ello no es suficiente en geometrías complejas, por lo cual es necesario utilizar mallas compuestas; tal tipo de mallas están conformadas por múltiples bloques interconectados. En el presente trabajo se muestra que las técnicas de descomposición de dominio proporcionan una metodología eficaz para resolver este tipo problemas; se obtiene primero la solución en la interfaz de las mallas interconectadas, o bloques, y después la solución en cada una de las mallas. Con el fin de validar la metodología, se realiza una comparación con soluciones analíticas. Se presenta un caso de aplicación.

Palabras clave: flujo con potencial, mallas compuestas, mallas curvilíneas, descomposición de dominio.

 

Abstract

A methodology for the numerical computation of potential flow using composite curvilinear grids is presented. Curvilinear grids can be adapted to physical domains with irregular geometry. However, in complex geometries this is not enough; in such cases, composite grids should be used, which are formed by multiple interconnected blocks. This paper shows that the use of domain decomposition techniques provides an efficient methodology for solving this kind of problems, obtaining the solution first at the interface, and later in each block. In order to validate the proposed methodology a comparison with analytical solutions is performed. An application case is also presented.

Keywords: potential flow, composite grids, curvilinear grids, domain decomposition.

 

Introducción

La teoría del flujo con potencial permite analizar flujos reales bajo la hipótesis de que son irrotacionales. Un flujo real está sujeto a deformaciones angulares y en principio no puede ser modelado con la teoría del flujo con potencial. Sin embargo, en ciertos casos puede considerarse como irrotacional; por ejemplo, si las fuerzas que generan el movimiento (como la gravedad o un gradiente de presiones) son grandes, en comparación con las de origen viscoso (Sotelo, 2008); en este caso, el flujo que se encuentra fuera de la capa viscosa se puede considerar irrotacional; a lo anterior se suma que no existan zonas de separación. Por tanto, el análisis de flujo con potencial proporciona una buena aproximación a la distribución de velocidades del flujo real en muchos casos prácticos.

La solución se obtiene con la ecuación de Laplace, que se resuelve con diferentes técnicas: numéricas, analíticas, mapeo conforme o por superposición de flujos simples, entre otras (Grenger, 1995). Las técnicas no numéricas tienen la desventaja de aplicarse sólo en algunos tipos de geometrías. En este trabajo se propone una metodología de solución numérica que utiliza mallas curvilíneas compuestas, las cuales son de uso más general, ya que permiten dar solución en situaciones donde la geometría del dominio es compleja, que difícilmente se resuelven con técnicas no numéricas y que es complicado discretizar con mallas de un único bloque (Thompson et al., 1999). Las mallas curvilíneas compuestas consisten en múltiples mallas interconectadas; conservan la ventaja de que cada bloque es estructurado. Después de un estudio bibliográfico se encontró que las técnicas de descomposición de dominio (ver por ejemplo Toselli y Widlund, 2005) plantean una metodología eficaz para dar solución a la ecuación de Laplace en geometrías que se dividen en dos o más subdominios.

 

Flujo con potencial

El flujo con potencial permite calcular el campo de velocidades a partir del potencial de velocidad, denotado como Φ. El campo de velocidades se obtiene con la relación:

En (1), es el campo de velocidades, definido como . Al combinar (1) y la ecuación de continuidad (Granger, 1995) se obtiene:

La ecuación (2) es la ecuación de Laplace para el potencial de velocidad. Otra manera de analizar el flujo con potencial es la función de corriente, ψ, la cual se relaciona con Φ a través de las condiciones de Cauchy-Riemann (Grenger, 1995). Este parámetro satisface también la ecuación de Laplace:

 

Condiciones de frontera

Las ecuaciones (2) y (3) están sujetas a condiciones de frontera tipo Newmann, Dirichlet o Cauchy (Saad, 2003). En este trabajo se presenta el caso que es una combinación de tipo Dirichlet en una región del contorno, y Newmann en la parte restante, debido a que corresponden con los tipos de fronteras manejadas (paredes impermeables y fronteras abiertas). Cuando se hace un análisis con Φ, lo común es conocer la magnitud del potencial en la entrada y la salida, y se manejan como fronteras Dirichlet. La parte restante de los contornos son paredes impermeables y se cumple la condición ∂Φ/∂n = 0, que es tipo Newmann. Cuando se resuelve con ψ, se conoce el valor de la función de corriente en las paredes, por lo que son tipo Dirichlet, mientras las fronteras abiertas son Newmann.

 

Solución empleando coordenadas curvilíneas

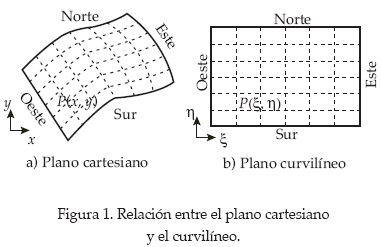
En las geometrías con forma irregular es común utilizar dos metodologías de solución numérica: una es con mallas no estructuradas y elemento finito (Segerlind, 1984); otra es con mallas curvilíneas (Thompson et al., 1999), con las que se pueden utilizar diferencias finitas. En este trabajo se utiliza la segunda metodología. El empleo de un sistema coordenado curvilíneo consiste en establecer una relación única entre el espacio cartesiano x - y, y el curvilíneo ξ - η, de tal forma que un dominio irregular en x - y se represente como un área rectangular en ξ - η. Lo anterior se indica en la figura 1, donde el área delimitada por cuatro fronteras irregulares en el lado izquierdo tiene una representación rectangular en el derecho. En la figura 1 se observa que el uso de este tipo de mallas (en su forma tradicional de un bloque) tiene la restricción de que el dominio en el plano cartesiano debe estar delimitado por cuatro fronteras, las cuales corresponden a los cuatro lados del rectángulo representado en el plano curvilíneo; esta restricción se elimina cuando se emplean mallas compuestas.

El sistema curvilíneo requiere de la transformación de las ecuaciones del flujo para referirlas a este sistema. Con este enfoque resulta sencillo implementar un esquema de diferencias finitas completamente idéntico para todos los nodos interiores de la malla debido a que ésta es rectangular. La transformación de las ecuaciones diferenciales parte de la regla de la cadena. Si se considera una función F cualquiera, la derivada respecto a x se calcula como:

La derivada respecto a y se calcula de manera semejante. Para evaluar estas derivadas se requiere conocer ∂(ξ,η)/∂(x,y), que se obtienen a partir del sistema coordenado curvilíneo. La base covariante del sistema curvilíneo se define como:

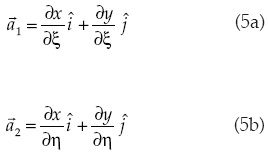
Los vectores anteriores son tangenciales a los ejes curvilíneos; la base contravariante, que es normal a los ejes, está dada por:

La base covariante se calcula numéricamente una vez que la malla ha sido generada, mientras que la base contravariante se obtiene a partir de la primera, con las expresiones (Thompson et al., 1985):

En (7), J es el Jacobiano de la transformación y es el vector unitario normal al plano coordenado. Los elementos métricos, necesarios para la transformación de la ecuación de Laplace, se obtienen a través del producto escalar de los vectores de la base contravariante:

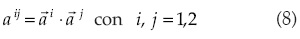
En Thompson et al. (1985) se explica la transformación de la ecuación de Laplace de coordenadas cartesianas a curvilíneas, que parte de las relaciones como la indicada en (4). Las ecuaciones (2) y (3) quedan expresadas en su forma curvilínea no conservativa, respectivamente como:

y

Las ecuaciones (9) y (10) son resueltas con un esquema de diferencias finitas centradas (Leveque, 2007). Teniendo en cuenta que en el plano curvilíneo Δξ = 1 y Δη = 1, y sustituyendo el esquema de diferencias, (9) se expresa como sigue:

Donde:

Los subíndices de Φ en (11) se refieren a la ubicación de los nodos en la malla curvilínea, tal como se indica en la figura 2. Al aplicar (11) en cada uno de los nodos de la malla curvilínea, incluyendo las condiciones de frontera, se obtiene un sistema de la forma AΦ = b, cuya solución es el potencial de velocidad. Se procede de manera análoga para la función de corriente ψ.

Con el potencial de velocidad conocido, el campo de velocidades se calcula con la ecuación (1), transformada a coordenadas curvilíneas:

 

Metodología

Las mallas compuestas consisten en una discretización del dominio físico, empleando dos o más mallas interconectadas entre sí. Como ejemplo, en la figura 3 se muestra un dominio discretizado con una malla conformada por nueve bloques.

El uso de las mallas compuestas requiere una metodología para hacer compatible la solución en la interfaz de los bloques. En este trabajo se emplean las técnicas de descomposición de dominio, como se explica en Chan y Mathew (1994), y Toselli y Widlund (2005), entre otras referencias.

 

Técnicas de descomposición de dominio

Estas técnicas se dividen en dos categorías: las primeras son denominadas técnicas con traslape, y las segundas, sin traslape. Las técnicas con traslape se aplican para resolver los sistemas de ecuaciones generados al segmentar un dominio Ω en múltiples subdominios Ω_i traslapados entre sí; mientras que las técnicas sin traslape se emplean cuando el dominio se divide en múltiples subdominios, cuya única conexión es a través de una interfaz Γ, tal como se indica en la figura 4.

En este trabajo se propone emplear la metodología sin traslape, ya que facilita la generación de la malla curvilínea y el manejo de la información. Si se considera que, por ejemplo, el dominio se descompone en dos subdominios, como se indica en la figura 4, al utilizar un esquema de diferencias finitas se obtiene un conjunto de nodos que pertenecen al subdominio Ω₁, otro conjunto de nodos que pertenecen a Ω₂ y finalmente un conjunto de nodos que pertenecen a la interfaz Γ. El sistema de ecuaciones obtenido tiene la estructura siguiente:

Los componentes involucrados en (14) son vectores y matrices; A₁ y A₂ son las matrices resultantes de las discretizaciones en los subdominios Ω₁ y Ω₂, mientras que la matriz A_Γ corresponde a la discretización de la interfaz Γ. Las matrices A_i,Γ y A_Γ,i establecen la interacción entre la interfaz y los subdominios. Finalmente, los vectores y son la solución en Ω₁, Ω₂ y Γ, respectivamente.

El sistema (14) está conformado por una matriz en bloque o matriz de matrices; puede resolverse con la eliminación de Gauss por bloques (Ortega, 1988), por lo que se obtiene el sistema equivalente:

En el sistema (15), la matriz S y el vector están definidos de la siguiente manera:

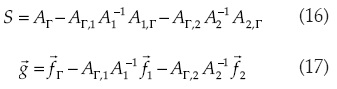
La solución en los nodos de la interfaz es obtenida al resolver el sistema de ecuaciones del último renglón en el sistema (15):

Una vez que se conoce , se obtienen las soluciones y al resolver los sistemas de ecuaciones asociados con los subdominios Ω₁ y Ω₂, ubicados en los renglones 1 y 2, respectivamente, del sistema (15):

Con los sistemas (18) al (20) se obtiene la solución del dominio completo. Las ecuaciones (16) y (17) corresponden a una descomposición en dos subdominios; sin embargo, la generalización para n subdominios es de la siguiente forma:

En (21) y (22), que proporcionan la matriz y el vector necesarios para obtener la solución en la interfaz por medio de (18), se observa que es necesario invertir las matrices de cada uno de los subdominios. Aunque en la literatura (Chan y Mathew, 1994) se recomienda resolver (14) de forma iterativa, en este trabajo se propone utilizar un método de solución directa. Esto involucra invertir las matrices de los subdominios para obtener la matriz S y el vector . Esto se debe a que en pruebas realizadas en diferentes mallas con un número de nodos de algunos miles, no resultó computacionalmente caro trabajar de esta manera. Las matrices inversas A_i^–1 pueden calcularse a través de la factorización LU, obteniéndose la matriz inversa de la forma:

Invertir las matrices A_i es siempre posible cuando sean no singulares (Saad, 2003), lo cual ocurre prácticamente en todos los casos para la ecuación de Laplace: los coeficientes (12) producen un sistema en banda donde la diagonal principal es dominante. Una ventaja de utilizar la factorización LU es que, una vez que se obtiene la solución en la interfaz a través de resolver (18), puede utilizarse el resultado de la factorización para resolver el sistema siguiente:

El sistema (24) es una generalización de (19) y (20).

Para ejemplificar el proceso de discretización utilizando una malla compuesta, se analiza el caso indicado en la figura 5, correspondiente a un dominio que se ha descompuesto en tres bloques. Los nodos se numeran consecutivamente, incluyendo los de la interfaz. Con esta numeración se obtiene el sistema de ecuaciones:

 

Además de la numeración global, cada bloque y la interfaz tienen numeración local, como se indica en el cuadro 1.

Las matrices componentes de (25) se obtienen a partir de la información mostrada en la figura 5, donde los bloques se representan en el espacio curvilíneo; en este ejemplo, por simplicidad se tiene como base contravariante y 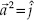, por lo que ∇²ξ = ∇²η = 0, y, como es costumbre en la malla curvilínea, se tiene ∇ξ = ∇η = 1. Al aplicar los coeficientes definidos por (12), para el nodo 1 se tiene que Φ_c = Φ₁, Φ_e = Φ₂ y Φ_n= Φ₃ que sustituidos en (11) da por resultado:

Los valores cruzados en (11), como por ejemplo Φ_ne, se cancelaron en (26) debido a que la malla es ortogonal. Las matrices para los bloques (25) quedan:

En el cuadro 1 se observa que cada bloque y la interfaz están formados por cuatro nodos, por ello las matrices A_i y A_Γ son en este caso de 4 × 4. Una vez que se tienen las matrices como se indican en (27) a (29), se procede a calcular las matrices S y (este último vector se obtiene con los componentes 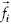, que se determinan con las condiciones de frontera) para obtener la solución en la interfaz, y posteriormente en cada uno de los bloques.

 

Validación del esquema

Se realiza la comparación de esta metodología con resultados analíticos. El caso corresponde a la superposición de un flujo uniforme más una fuente; la función de corriente es ψ = ψ_uniforme + ψ_fuerte (Granger, 1995), que reproduce el flujo alrededor de un obstáculo, como el de la figura 6a. La ecuación de la función de corriente, en coordenadas polares (r,θ), es la siguiente:

 

donde U es la velocidad del flujo uniforme y q es el caudal unitario en la fuente. Con (30) se obtienen las líneas de corriente indicadas en la figura 6a, donde se utiliza U = 2 m/s y q = 20 m²/s. El dominio empleado para la solución numérica es el delimitado por las líneas de corriente ψ =-190 m²/s en el sur, ψ = 210 m²/s en el norte, y por las rectas x = 140 m en el este, y x =-140 m en el oeste. En el norte y sur se tienen fronteras tipo Dirichlet, mientras que en el este y oeste son tipo Newman. La parte correspondiente al obstáculo se maneja como Dirichlet con ψ = 10 m²/s. Se emplean cuatro bloques para discretizar el dominio, tal como se indica en la figura 6b.

Se compara la solución analítica con la obtenida numéricamente en la recta A-A', indicada en la figura 6a. Los resultados analítico y numérico se muestran en la figura 7; en términos prácticos, son los mismos.

 

Aplicación

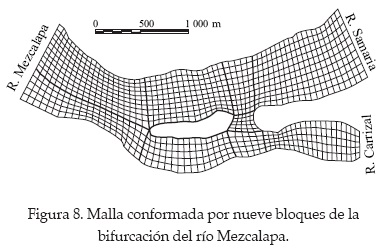
Se estudia la bifurcación del río Mezcalapa en los ríos Samaria y Carrizal; en este caso se calculó el campo de velocidades y la distribución de gastos en los dos ríos de salida. La malla se indica en figura 8 y está conformada por 1 040 nodos. En la entrada del río Mezcalapa el potencial de velocidad se estableció como Φ = 4 000 m²/s, y en las salidas de los ríos Samaria y Carrizal como Φ = 0 m²/s. Por otra parte, las márgenes de los ríos se manejaron como fronteras tipo Newmann, esto es, ∂Φ/ ∂n = 0.

Se resolvió para el potencial de velocidad debido a que puede asociarse intuitivamente con el tirante, h, ya que el sentido del campo de velocidades ocurre hacia donde hay un gradiente negativo de h.

La distribución de gastos se muestra en el cuadro 2. El campo de velocidades calculado se indica en la figura 9. Debe tenerse en cuenta que el caudal obtenido es unitario respecto a la dirección perpendicular al plano.

 

 

Conclusiones

La teoría del flujo con potencial sigue siendo una herramienta útil cuando la física del problema permite considerar al flujo como irrotacional. En este trabajo se presenta una metodología de solución alternativa cuando se tienen geometrías donde es complicado utilizar una solución no numérica o que resulta difícil de discretizar con una malla de un único bloque.

Un aspecto importante a considerar es que aunque la metodología aquí presentada se aplicó al flujo con potencial, puede utilizarse en cualquier otro tipo de problemas, donde el dominio físico requiera una discretización basada en mallas compuestas, debido a que las técnicas de descomposición de dominio permiten dividir un problema grande en múltiples problemas más pequeños. Cualquier esquema numérico de solución de ecuaciones diferenciales parciales que dé como resultado un sistema de ecuaciones lineales puede resolverse eficientemente con el planteamiento de mallas compuestas presentado en este trabajo.

 

Agradecimientos

Al Consejo Nacional de Ciencia y Tecnología por el apoyo a esta investigación.

 

Referencias

CHAN, T.F. and MATHEW, T.P. Domain decomposition algorithms. Acta Numérica 1994. Vol. 3, 1994, pp. 61-143.         [ Links ]

GRANGER, R.A. Fluid Mechanics. New York: Dover Publications, 1995, 896 pp.         [ Links ]

LEVEQUE, R. Finite difference methods for ordinary and partial differential equations. Philadelphia: SIAM, 2007, 341 pp.         [ Links ]

ORTEGA, Y.M. Introduction to parallel and vector solution of linear systems. New York: Plenum Press, 1988, 305 pp.         [ Links ]

SOTELO, A.G. Hidráulica General. México, D.F: Editorial Noriega, 2008, 561 pp.         [ Links ]

SAAD, Y. Iterative methods for sparse linear Systems. Philadelphia: SIAM, 2003, 528 pp.         [ Links ]

SEGERLIND, L.J. Applied Finite Element Analysis. New York: John Wiley & Sons Inc., 1984, 427 pp.         [ Links ]

THOMPSON, J.F., Warsi, Z., and WAYNE, C. Numerical grid generation, foundations and applications. New York: Elsevier Science Publishing, 1985, 483 pp.         [ Links ]

THOMPSON, J.F., SONI, B.K., and WEATHERILL, N.P. Handbook of grid generation. Florida, USA: CRC Press, 1999, 950 pp.         [ Links ]

TOSELLI, A. and WIDLUND, O. Domain decomposition methods-algorithms and theory. Berlin: Springer, 2005, 450 pp.         [ Links ]