Artículos técnicos

 

Modelo hidrodinámico completo para riego por melgas

 

Complete hydrodynamic model for border irrigation

 

Heber Saucedo¹, Manuel Zavala² y Carlos Fuentes³

 

¹ Instituto Mexicano de Tecnología del Agua.

² Universidad Autónoma de Zacatecas, México.

³ Universidad Autónoma de Querétaro, México.

 

Dirección institucional de los autores

Dr. Heber Saucedo

Instituto Mexicano de Tecnología del Agua
Paseo Cuauhnáhuac 8532, colonia Progreso
62550 Jiutepec, Morelos, México
Teléfono: +52 (777) 3293 600, extensión 443
hsaucedo@tlaloc.imta.mx

Dr. Manuel Zavala

Universidad Autónoma de Zacatecas
Avenida López Velarde 801, Centro
98000 Zacatecas, Zacatecas, México
mzavala73@yahoo.com.mx

Dr. Carlos Fuentes

Universidad Autónoma de Querétaro
Cerro de las Campanas s/n
76010 Santiago de Querétaro, Querétaro, México
cfuentesr@gmail.com

 

Recibido: 17/02/09
Aprobado: 16/08/10

 

Resumen

Se presenta un modelo numérico para riego por melgas basado en el acoplamiento interno de las ecuaciones de Saint-Venant y Richards, el cual permite describir las fases de avance, almacenamiento, consumo y recesión del riego por melgas. La solución de las ecuaciones de Saint-Venant se aproxima utilizando un esquema Lagrangiano en diferencias finitas, mientras que para la ecuación de Richards se utilizan elementos finitos para la integración en el espacio y diferencias finitas implícitas para la integración en el tiempo. Los resultados obtenidos permiten concluir que el modelo puede ser utilizado con fines de diseño de riego por melgas.

Palabras clave: fase de avance, fase de almacenamiento, fase de consumo, fase de recesión, acoplamiento numérico interno.

 

Abstract

A numerical model for border irrigation is presented-based on the internal coupling of Saint-Venant and Richards equations-that makes it possible to describe the advance, wetting, depletion, and recession phases. The solution of Saint-Venant equations is approached by a finite-difference Lagrangian scheme, while for Richards equation finite elements for the space discretization and implicit finite-differences for the time discretization are used. The results obtained with the model application lead to conclude that the model can be used for border irrigation design.

Keywords: advance phase, wetting phase, depletion phase, recession phase, internal numerical coupling.

 

Introducción

La descripción del flujo del agua en el riego por melgas requiere tener en cuenta las ecuaciones de Saint-Venant para describir el flujo del agua sobre la superficie del suelo y la ecuación de Richards para modelar el flujo del agua en el suelo, de tal manera que su acoplamiento permita conocer las formas de los perfiles de flujo superficial y la distribución de los potenciales de presión en el suelo según avanza el riego. El tirante proporcionado por las ecuaciones de Saint-Venant se utiliza para definir una condición de frontera tipo Dirichlet para la ecuación de Richards, cuya solución numérica permite el cálculo de la lámina infiltrada, necesaria para la solución de las ecuaciones de Saint-Venant, teniéndose, por lo tanto, un procedimiento iterativo.

Los principales trabajos de modelación del riego por gravedad pueden diferenciarse según el tipo de ecuaciones que emplean para representar el fenómeno. Respecto a la modelación del flujo de agua a superficie libre sobre el suelo, se emplean básicamente cuatro aproximaciones: modelo hidrológico o de balance de volumen, onda cinemática, onda difusiva y ecuaciones de Saint-Venant completas. Para la representación del flujo del agua en el suelo se utilizan principalmente tres aproximaciones: la ley de infiltración empírica de Kostiakov (1932), leyes de infiltración con base físico-matemática e hipótesis simplificadoras: ecuación de Green y Ampt (1911), ecuación de Philip (1957) y ecuación de Parlange et al. (1982), y ley de infiltración conforme a la ecuación de Richards (1931).

En la literatura relacionada con el tema de este trabajo se reportan diversos modelos para simular el flujo del agua en el riego por melgas, los cuales difieren por la forma en que se aproxima la descripción tanto del flujo del agua a superficie libre como del flujo del agua en el suelo, en este contexto pueden citarse trabajos en los que el comportamiento del medio poroso se modela mediante leyes de infiltración con formas potenciales, como la ecuación de Kostiakov-Lewis (Sakkas y Strelkoff, 1974; Strelkoff y Katopodes, 1977; Katopodes y Strelkoff, 1977; Abiola y Katopodes, 1988; Catalán et al., 1988; Wallender y Rayej, 1990; Bautista y Wallender, 1992; Playán et al., 1994; García, 1994; Vivekanad y Bhallamundi, 1995), o bien utilizado la ecuación de Parlange (Schmitz et al., 1985; Vivekanad y Bhallamundi, 1995) o la ecuación de Philip (Philip y Farrell, 1964; Or y Walker, 1996). Recientemente se han desarrollado modelos que utilizan ecuaciones diferenciales bidimensionales para describir el flujo del agua en el suelo (Bradford y Katopodes, 1998; Saucedo et al., 2005; Banti et al., 2007; Bautista et al., 2010). En relación con los dos últimos trabajos citados, los más recientes, Banti et al. (2007), proponen un modelo basado en el uso de las ecuaciones de Saint-Venant y Richards, pero difieren significativamente al desarrollado en este trabajo en la forma de resolver numéricamente las ecuaciones de Saint-Venant, ya que en el artículo citado se emplea un esquema numérico tipo MacCormack, cuya aplicación requiere del uso de la hipótesis de un tirante pequeño presente sobre toda la melga desde el inicio del riego, lo cual no guarda concordancia con la física del riego por melgas; en el presente trabajo se prescinde de dicha hipótesis, al emplear un método euleriano-lagrangiano basado en Strelkoff y Katopodes (1977), el cual permite seguir detalladamente la evolución del frente de avance. El trabajo de Bautista et al. (2010) presenta un análisis de la naturaleza del acoplamiento de las ecuaciones empleadas para modelar el riego por melgas, y propone el empleo de un acoplamiento externo, diferente al acoplamiento interno utilizado en este trabajo; según los autores citados, el acoplamiento externo reduce el tiempo de cómputo y mejora la convergencia. En comparación con el trabajo presentado, puede decirse que con el empleo de nuevas computadoras es posible reducir el tiempo de cómputo, y que la mejora en la convergencia puede alcanzarse reduciendo los pasos de tiempo y espacio en el modelo presentado en este trabajo.

En el riego por melgas pueden distinguirse cuatro fases: avance, almacenamiento, consumo y recesión. La fase de avance inicia con la introducción del agua en la melga y termina cuando el frente de onda alcanza el extremo aguas abajo de la melga. La fase de almacenamiento comienza cuando el frente de onda llega al extremo aguas abajo de la melga y culmina cuando se deja de aplicar el gasto de aporte en la cabecera. La fase de consumo inicia cuando se deja de aplicar el gasto de aporte en la cabecera de la melga y culmina cuando se tiene un tirante nulo en dicha posición. La fase de recesión comienza a partir de que se tiene un tirante de agua nulo en la cabecera de la melga y termina cuando se alcanza un tirante de agua nulo en el extremo aguas abajo de la melga. El objetivo de este trabajo es desarrollar un modelo basado en el acoplamiento numérico interno de las ecuaciones de Saint-Venant y Richards que permita describir todas las fases del riego por melgas.

 

Flujo del agua sobre la superficie del suelo

El flujo del agua con una superficie libre es modelado con las ecuaciones de Saint-Venant, que resultan de la aplicación de las leyes de conservación de masa y cantidad de movimiento. En una melga, la relación entre su ancho y el tirante de agua permite considerar las ecuaciones correspondientes al escurrimiento sobre una superficie de ancho infinito (Woolhiser, 1975). La ecuación de continuidad se escribe como:

La ecuación de momentum se escribe en la forma recomendada por Saucedo et al. (2005):

donde q(x,t) = U(x,t)h(x,t) es el gasto por unidad de ancho de melga [L²T^-1]; x, la coordenada espacial en la dirección principal del movimiento del agua en la melga [L]; t, el tiempo [T]; U, la velocidad media; h, el tirante de agua [L]; J_o, la pendiente topográfica de la melga [LL^-1]; J, la pendiente de fricción [LL^-1]; V_I = ∂I/∂t, el flujo de infiltración [LT^-1], es decir, el volumen de agua infiltrado en la unidad de tiempo por unidad de ancho y por unidad de longitud de la melga; I, la lámina infiltrada [L]; g, la aceleración gravitacional [LT^-2]; el parámetro adimensional β = 1 - α, siendo α = 1 - U_Ix/U, donde U_Ix es la proyección en la dirección del movimiento de la velocidad de salida de la masa de agua debido a la infiltración.

La relación entre las variables hidráulicas q y h con la pendiente de fricción, denominada ley de resistencia hidráulica, es adoptada de acuerdo con Fuentes et al. (2004), haciendo uso de una ley potencial de resistencia:

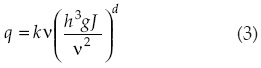
donde ν es el coeficiente de viscosidad cinemática del agua [L²T^-1] y k es un factor adimensional.

Para establecer las condiciones inicial y de frontera que deben sujetar a las ecuaciones de Saint-Venant para modelar las cuatro fases del riego por melgas, se tiene en cuenta una melga cerrada, a fin de evitar la pérdida de masa fuera del dominio de riego. Para la fase de avance se tiene:

donde x_ƒ(t) es la posición del frente de onda para el tiempo t y q_o es el gasto de aporte en la entrada de la melga. Para la fase de almacenamiento:

donde L es la longitud de la melga y q_o es el gasto de aporte en la cabecera de la melga. Para la fase de consumo:

Para cerrar el sistema es necesario conocer la forma en que evoluciona en el tiempo la lámina infiltrada en toda posición sobre la melga, es decir, la ley de infiltración, la cual es proporcionada con base en la solución de la ecuación de Richards (1931).

 

Flujo del agua en el suelo

La descripción del proceso de infiltración del agua en el suelo puede efectuarse teniendo como base la ecuación de Richards (1931), que resulta de la combinación de la ecuación de continuidad con el campo de velocidades calculado conforme a la ley de Darcy y que en su forma tridimensional, sin tener en cuenta la extracción de agua por las plantas, se escribe como:

donde ψ es el potencial de presión del agua en el suelo, expresado como la altura de una columna equivalente de agua [L] (positivo en la zona saturada y negativo en la zona no saturada del suelo); C(ψ) = dθ/dψ es denominada la capacidad específica de humedad del suelo; θ = θ (ψ) es el volumen de agua por unidad de volumen de suelo o contenido volumétrico de agua [L³L^-3] y es una función de ψ conocida como curva característica de humedad o curva de retención del agua; K = K(ψ) es la conductividad hidráulica [LT^-1], que en un suelo parcialmente saturado es una función del potencial de presión; el potencial gravitacional es asimilado a la coordenada espacial z orientada positivamente hacia abajo [L]; ∇ = (∂/∂x,∂/∂y,∂/∂z) es el operador gradiente; x, y son las otras dos coordenadas espaciales [L], y t es el tiempo [T].

El riego es un fenómeno que se efectúa en tres dimensiones, lo cual hace necesario que el flujo del agua en el suelo sea descrito utilizando la ecuación (8), sin embargo, es conveniente aceptar la hipótesis de que el fenómeno se efectúa en planos paralelos al desarrollo de la melga; entonces es posible utilizar la forma bidimensional de la ecuación de Richards:

la cual debe resolverse sobre el dominio de solución que se muestra en la figura 1.

Como condición inicial para la solución de la ecuación de Richards bidimensional se debe especificar la distribución de las presiones en el espacio:

Las condiciones de frontera correspondientes pueden considerarse como sigue: frontera tipo Dirichlet con potencial prescrito conforme a la solución de las ecuaciones de Saint-Venant, y fronteras tipo Neumann con flujo nulo, frontera bajo gradiente unitario:

la profundidad del dominio de solución (P) debe ser mayor que la máxima posición del frente de humedecimiento durante el riego.

La solución de la ecuación de Richards hace indispensable representar las propiedades hidrodinámicas del suelo, expresando el potencial de presión (ψ) como una función del contenido volumétrico de agua (θ) y la conductividad hidráulica K como una función de θ. Como es señalado por Fuentes et al. (1992), la combinación de las características hidrodinámicas de Fujita (1952) y Parlange et al. (1982) es conveniente en estudios teóricos, como la construcción de soluciones analíticas exactas; en estudios experimentales puede ser más conveniente la utilización de la combinación de la curva de retención propuesta por van Genuchten (1980), considerando la restricción de Burdine (1953) con la curva de conductividad hidráulica propuesta por Brooks y Corey (1964), debido a que satisfacen las propiedades integrales de la infiltración y a la facilidad para la identificación de sus parámetros.

La curva de retención propuesta por van Genuchten (1980) se escribe como: [θ (ψ) -θ_r]/[θ_s -θ_r] = [1+ (ψ/ψ_d)ⁿ]^-m, donde ψ_d es un valor característico de la presión del agua en el suelo, m y n son dos parámetros de forma empíricos relacionados por la restricción de Burdine (1953): m = 1 - 2/n, con 0 < m < 1 y n > 2, θ_s; es el contenido volumétrico de agua a saturación efectiva del suelo y θ_r es el contenido volumétrico de agua residual. La conductividad hidráulica propuesta por Brooks y Corey (1964) se representa como K(θ) = K_s [(θ -θ_r)/(θ_s -θ_r)]^η, donde η es un parámetro de forma empírico y positivo.

La lámina infiltrada se calcula para cada posición x_i, donde se resuelven numéricamente las ecuaciones de Saint-Venant:

donde F es la posición del frente de humedecimiento y θ(x_i,z,0) es el contenido volumétrico de agua inicial.

 

Solución numérica

El esquema numérico para la fase de avance ha sido expuesto por los autores (Saucedo et al., 2005). La disposición de las celdas de cálculo para las fases de avance, almacenamiento, consumo y recesión se muestra en la figura 2. La configuración de las celdas para la fase de recesión obedece al hecho de que en lugar de utilizar un esquema de paso de tiempo constante, se hace uso de un esquema de paso de espacio fijo.

La forma discreta de la ecuación de continuidad para las fases de almacenamiento, consumo y recesión se escribe como:

para la ecuación de momentum, la forma discreta es:

donde los coeficientes se calculan a partir de los valores pertenecientes al nivel de tiempo anterior: 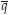= (1 - Φ)q_m + Φq_j, = (1 - Φ)h_m + Φh_j (Saucedo et al., 2005).

Se introducen las variables pequeñas (Strelkoff y Katopodes, 1977): y , tales que, para las celdas interiores se tiene: . Se sustituyen en las formas discretas de las ecuaciones de continuidad y momentum, y se obtiene un sistema de ecuaciones algebraicas, cuya solución permite avanzar en el tiempo los valores de las variables hidráulicas.

 

Fase de almacenamiento

Debido que en la última celda se tiene un tirante nulo en la punta de la onda al inicio de la fase de almacenamiento, el cual no sirve para aproximar el tirante en el tiempo siguiente, se emplea solamente en esa etapa, denominada de enlace, el tirante que se tiene en un punto anterior en el espacio para avanzar los perfiles de flujo. La etapa cuasi-estacionaria se tiene una vez que el tirante en el extremo aguas abajo de la melga es diferente de cero, y se emplea para estimar el tirante en el tiempo siguiente y avanzar los perfiles de flujo. Para la última celda en la etapa de enlace se tiene 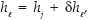,, mientras que para la etapa cuasi-estacionaria se escribe,; puede apreciarse que la forma de las aproximaciones en ambas etapas difiere en el cálculo de h_r. Las expresiones que se obtienen para el sistema matricial se muestran en el anexo.

 

Fase de consumo o recesión vertical

La fase de consumo o de recesión vertical comienza una vez que se tiene en el dominio de solución una cantidad de agua que permite disponer de una lámina media igual a la lámina de riego que desea aplicarse, y termina en el momento en que se consume el agua en la cabecera de la melga, dando inicio a la fase de recesión. Para modelar la fase de consumo se utilizan las aproximaciones de la fase de almacenamiento en su etapa cuasi-estacionaria, considerando la eliminación del gasto en la cabecera de la melga en el cálculo de la primera celda. Las entradas del sistema matricial para la primera celda se muestran en el anexo, mientras que para las celdas interiores y la última celda se hace uso de las ecuaciones para dichos tipos de celda empleadas en la fase de almacenamiento.

 

Fase de recesión

La fase de recesión ha sido modelada mediante un esquema con paso de espacio constante (δx), que permite evitar los errores que se involucran en la reproducción del frente de recesión cuando se hace uso de un esquema con paso de tiempo constante; dichos errores tienen que ver con el hecho de que difícilmente se obtiene un tirante nulo en una posición de la malla donde se resuelven las ecuaciones de Saint-Venant para un tiempo que sea múltiplo del paso de tiempo constante empleado en la discretización, motivando que el frente de recesión se corra de manera anticipada al nudo siguiente; no obstante que esta aproximación produce errores de balance poco significativos si se agrega a la lámina infiltrada el tirante que permanece sobre el nudo desde el cual se efectúa la traslación del frente de recesión, es posible mejorar la aproximación utilizando un esquema con paso de espacio constante. Es necesario realizar una interpolación entre las variables tanto de las ecuaciones de Saint-Venant como de la ecuación de Richards para pasar de la malla de paso de espacio variable utilizada en las fases de consumo a una malla de paso de espacio constante.

La utilización de un esquema de paso de espacio constante genera un sistema de ecuaciones, en el cual el número de incógnitas es inferior en dos unidades al número de ecuaciones, motivo por el que se acepta no resolver la ecuación de conservación de momentum en la primera y la última de las celdas de cálculo. El paso de tiempo se calcula utilizando las variables hidráulicas de la primera celda, teniendo en cuenta la forma discreta de la ecuación de continuidad:

es importante señalar que se desconoce a priori el valor de I_r, motivo por el cual es necesario proporcionar un estimador inicial, en este caso se tienen en cuenta los valores de lámina infiltrada correspondientes al nudo de coordenada r en los dos niveles de tiempo anteriores, de tal forma que es posible aproximar la velocidad de infiltración y calcular el primer estimador como I_r¹ = I_m + V_Iδt, donde V_I = (I_r^k-1 - I_r^k-2)/δt, siendo k el nivel de tiempo, y se resuelve la ecuación (19) para el paso de tiempo mediante un procedimiento iterativo. Con el valor del paso de tiempo así obtenido se avanzan los perfiles de flujo superficial y subsuperficial, resolviendo el sistema de ecuaciones que se muestra en el anexo.

 

Solución numérica de la ecuación de Richards

La ecuación de Richards bidimensional es discretizada en el espacio utilizando elementos finitos y en el tiempo mediante un esquema implícito en diferencias finitas. El procedimiento se encuentra bien documentado en la literatura y puede consultarse, por ejemplo, en Saucedo et al. (2002). La solución del sistema de ecuaciones algebraicas que resulta de la aplicación del método del elemento finito es efectuada usando el método del gradiente conjugado precondicionado (Noor y Peters, 1987).

 

Aplicación

Con la finalidad de verificar el funcionamiento del modelo desarrollado para las cuatro fases del riego por melgas, basado en el acoplamiento numérico interno de las ecuaciones de Saint-Venant y Richards, se realiza una aplicación empleado datos de un experimento reportado por Fuentes (1992). Se dispone de los siguientes datos: gasto unitario q_o = 0.0032 m³/s/m; pendiente topográfica J_o = 0.002 m/m; longitud de la melga L = 100 m; parámetros para la ley de resistencia de Fuentes et al. (2004) d = 1, k = 1/54; parámetro en la ecuación de cantidad de movimiento β = 2; valor inicial del contenido volumétrico de agua θ_o = 0.2749 cm³/cm³. Los parámetros θ_s, θ_r, m y η de las características hidrodinámicas fueron determinados a partir de la curva granulométrica del suelo franco de Montecillo. Siguiendo la metodología sugerida por Fuentes (1992) resulta θ_s = 0.4865 cm³/cm³, θ_r = 0.0 cm³/cm³, m = 0.1258, n = 2.2878 y η = 11.0. Los valores de los parámetros ψ_d = -32.75 cm y K_s = 1.84 cm/h se obtuvieron mediante la aplicación de un procedimiento inverso para describir datos de una prueba de riego efectuada en el experimento mencionado.

Se ha utilizado un paso de tiempo constante δt = 0.5 s tanto para las ecuaciones de Saint-Venant como para la ecuación de Richards. Para la ecuación de Richards se utilizaron pasos de espacio mínimo y máximo: ∆z_mín = 0.02 cm y ∆z_máx = 1.0 cm, ∆x_mín = 0.02 cm y ∆x_máx = 1.0 cm. La discretización utilizada guarda semejanza con las reportadas en la literatura, e.g., Strelkoff y Katopodes (1977): δt_mín = 5 s, Akanbi y Katopodes (1988): δt_máx = 1 s, para las cuales se reportan resultados consistentes en las variables hidráulicas del riego. La discretización para la ecuación de Richards es más fina que la reportada por Saucedo et al. (2002), quienes comparan perfiles de humedad proporcionados por una solución analítica exacta con los obtenidos mediante una solución numérica para la ecuación de Richards; los valores del error relativo máximo para el caso de dos suelos contrastantes: una arcilla clara de Yolo, Estados Unidos, y una arena del río Isére, Francia, presentan una cota superior de 0.25% cuando se utiliza un paso de tiempo máximo δt_máx = 30 s y pasos de espacio mínimo y máximo ∆z_mín = 0.04 cm y ∆z_máx = 10.0 cm. El suelo franco de Montecillo tiene un comportamiento hidrodinámico intermedio entre los que presentan los suelos tratados por estos autores; en consecuencia, con la discretización utilizada, el error relativo máximo debe tener como una cota superior 0.25%.

En la figura 3 se muestran los perfiles de flujo obtenidos durante la fase de avance y en la figura 4, las curvas de avance y recesión para la melga cerrada. En la figura 5 se tiene un detalle del comportamiento de los tirantes de agua en la parte final de la melga durante la fase de almacenamiento. La figura 6 muestra las cuatro fases del riego por melgas. En la figura 7 se representa la evolución y recesión vertical del tirante en la cabecera de la melga vista a través del comportamiento del potencial de presión. En la figura 8 se tiene la evolución del potencial de presión proporcionado por la ecuación de Richards bidimensional a lo largo de la melga durante la fase de recesión.

En la figura 9 se muestra el buen ajuste que presenta la respuesta del modelo hidrodinámico a datos de avance registrados en el experimento reportado por Fuentes (1992).

 

Conclusiones

Se ha desarrollado un modelo numérico para riego por melgas basado en el acoplamiento interno de las ecuaciones de Saint-Venant y Richards, el cual permite describir las fases de avance, almacenamiento, consumo y recesión del riego por melgas. La solución de las ecuaciones de Saint-Venant se aproxima utilizando un esquema Lagrangiano en diferencias finitas, mientras que para la ecuación de Richards se utilizan elementos finitos para la integración en el espacio y diferencias finitas implícitas para la integración en el tiempo. Los resultados obtenidos permiten concluir que el modelo puede ser utilizado con fines de diseño de riego por melgas.

 

Referencias

ABIOLA, A. and KATOPODES, N. Model for flow propagation on initially dry land. Journal of Hydraulic Engineering. Vol. 114, No. 7, 1988.         [ Links ]

AKANBI, A. and KATOPODES, N. Model for flow propagation on initially dry land. Journal of Hydraulic Engineering. Vol. 114, No. 7, 1988.         [ Links ]

BANTI, M., ZISSIS, Th., and ANASTACIADDOU-PARTHENIOU, E. Numerical simulation of surface-subsurface flow interaction during irrigation. Geophysical Research Abstracts. Vol. 9, 07018, 2007.         [ Links ]

BAUTISTA, E. and WALLENDER, W. Hydrodynamic furrow irrigation model with specified space steps. Journal of Irrigation and Drainage Engineering. Vol. 118, No. 3, 1992.         [ Links ]

BAUTISTA, E., ZERIHUN, D., CLEMMENS, A.J., and STRELKOFF, T.S. External iterative copuling strategy for surface-subsurface flor calculations in surface irrigation. Journal of Irrigation and Drainage Engineering. Vol. 136, No. 10, 2010, pp. 692-703.         [ Links ]

BRADFORD, S. and KATOPODES, N. Nonhyydrostatic model for surface irrigation. Journal of Irrigation and Drainage Engineering. Vol. 124, No. 4, 1998.         [ Links ]

BROOKS, R.H. and COREY, A.T. Hydraulic properties of porous media. Hydrol. Pap. 3. Fort Collins: Colorado State University, 1964.         [ Links ]

BURDINE, N.T. Relative permeability calculation from size distributions data. Transactions AIME. Vol. 198, 1953, pp. 171-199.         [ Links ]

CATALÁN, E.A., CHÁVEZ, J., PALACIOS, O., CUEVAS, B. y FUENTES, C. Modelo hidrodinámico para la predicción del avance en el riego por melgas. Sobretiro de Agrociencia. Núm. 73, 1988.         [ Links ]

FUENTES, C. Approche fractale des transferts hydriques dans les sols non saturès. Tesis de Doctorado. Grenoble: Universidad Joseph Fourier, 1992, 267 pp.         [ Links ]

FUENTES, C., HAVERKAMP, R. and PARLANGE, J.-Y. Parameter constraints on closed-form soil-water relationships. Journal of Hydrology. Vol. 134, 1992, pp. 117-142.         [ Links ]

FUENTES, C., DE LEÓN, B., SAUCEDO, H., PARLANGE, J.Y. y ANTONINO, A. El sistema de ecuaciones de Saint-Venant y Richards del riego por gravedad: 1. La ley potencial de resistencia hidráulica. Ingeniería hidráulica en México. Vol. XVIII, núm. 2, 2004, pp. 121-131.         [ Links ]

FUJITA, H. The exact pattern of a concentration-dependent diffusion in a semi-infinite medium, part I. Textile Research Journal. Vol. 22, 1952, pp. 757-761.         [ Links ]

GARCÍA, N.H. Simulación numérica de flujo intermitente para diseño de riego parcelario por gravedad. Tesis de doctorado. México, D.F.: Universidad Nacional Autónoma de México, 1994, 316 pp.         [ Links ]

GREEN, W.H. and AMPT, G.A. Studies in soil physics, I: the flow of air and water through soils. J. Agric. Sci. Vol. 4, 1911, pp. 1-24.         [ Links ]

KATOPODES, D.N. and STRELKOFF, T. Hydrodynamics of border irrigation, complete model. Journal of the Irrigation and Drainage Division. IR3:309-324. 13188, 1977.         [ Links ]

KOSTIAKOV, A.N. On the dynamics of the coefficient of water-percolation in soils and on the necessity for studying it from a dynamic point of view for purposes of amelioration. Trans. Sixth International Society of Soil Science, Russian Part A, 1932, pp. 17-21.         [ Links ]

NOOR, K.A. and PETERS, J.M. Preconditioned Conjugate Gradient Technique for the analysis of symmetric structures. International Journal of Numerical Methods in Engineering. Vol. 24, 1987, pp. 2057-2070.         [ Links ]

OR, D. and WALKER, W.R. Effects of spatially variable intake on surface irrigation advance. Journal of Irrigation and Drainage Engineering. Vol. 122, No. 2, 1996.         [ Links ]

PARLANGE, J.-Y., BRADDOCK, R.D., LISLE, I., and SMITH, R.E. Three parameter infiltration equation. Soil Sci. Vol. 111, 1982, pp. 170-174.         [ Links ]

PHILIP, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. Vol. 83, 1957, pp. 345-357.         [ Links ]

PHILIP, J.R. and FARRELL D.A. General solution of the infiltration-advance problem in irrigation hydraulics. Geop. Res. Vol. 69, No. 4, 1964, pp. 621-631.         [ Links ]

PLAYÁN, E., WALKER, W.R., and MERKLEY, G.P. Two-dimensional simulation of basin irrigation. II: Applications. Journal of Irrigation and Drainage Engineering. Vol. 120, No. 5, 1994.         [ Links ]

RICHARDS, L.A. Capillary conduction of liquids through porous mediums. Physics 1. 1931, pp. 318-333.         [ Links ]

SAKKAS, G.J. and STRELKOFF, T. Hydrodynamics of surface irrigation, advanced phase. Journal of the Irrigation and Drainage Division. IR1:31-48. 10422, 1974.         [ Links ]

SAUCEDO, H., FUENTES, C., ZAVALA, M. y VAUCLIN, M. Una solución de elemento finito para la transferencia de agua en un sistema de drenaje agrícola subterráneo. Ingeniería hidráulica en México. Vol. XVII, núm. 1, 2002, pp. 93-105.         [ Links ]

SAUCEDO, H., FUENTES, C. y ZAVALA, M. El sistema de ecuaciones de Saint-Venant y Richards del riego por gravedad: 2. Acoplamiento numérico para la fase de avance en el riego por melgas. Ingeniería hidráulica en México. Vol. XX, núm. 2, 2005, pp. 109-119.         [ Links ]

SCHMITZ, G., HAVERKAMP, R. and PALACIOS, O. A coupled surface subsurface model for shallow water flow over initially dry soil. 21st Congress of the International Association for Hydraulic Research, Melbourne, Australia, 1985.         [ Links ]

STRELKOFF, T. and KATOPODES, N. Border-irrigation hydraulics with zero inertia. Journal of the Irrigation and Drainage Division. IR3:325-342. 13189, 1977.         [ Links ]

STRELKOFF, T. and KATOPODES, N. Border-irrigation hydraulics with zero inertia. Journal of the Irrigation and Drainage Division. Vol. IR3, 1977, pp. 325-342.         [ Links ]

VAN GENUCHTEN, M.TH. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Amer. J. Vol. 44, 1980, pp. 892-898.         [ Links ]

VIVEKANAD, S. and BHALLAMUNDI S.M. Complete hydrodynamic border-stripirrigation model. Journal of Irrigation and Drainage Engineering. Vol. 122, No. 4, 1995.         [ Links ]

WALLENDER, W. and RAJEY, M. Shotting method for Saint-Venant equations of furrow irrigation. Journal of Irrigation and Drainage Engineering. Vol. 116, No. 1, 1990.         [ Links ]

WOOLHISER, D.A. Simulation ofnsteady overland flow. In Unsteady flow in open channels. Mahmood, K. and Yevjevich, V. (editors). Fort Collins: Water Resources Publications. Vol. II, 1975, pp. 485-508.         [ Links ]