Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Tecnología y ciencias del agua
On-line version ISSN 2007-2422
Tecnol. cienc. agua vol.1 n.4 Jiutepec Oct./Dec. 2010
Artículos técnicos
Evaluación de riesgos en proyectos hidráulicos de ingeniería. Incertidumbres y confiabilidad
Risk assessment in hydraulic engineering projects: uncertainties and reliability
Humberto Marengo1, Felipe I. Arreguín2, Ignacio Romero3
1 Comisión Federal de Electricidad, México.
2 Comisión Nacional del Agua, México.
3 Comisión Federal de Electricidad, México.
Dirección institucional de los autores
Dr. Humberto Marengo
Coordinador de Proyectos Hidroeléctricos
Comisión Federal de Electricidad
Río Mississippi 71, colonia Cuauhtémoc
06500 México, D.F., México
Teléfonos: +52 (55) 5229 4400 y 5525 5769
Fax: +52 (55) 5207 0287
humberto.marengo@cfe.gob.mx
Dr. Felipe I. Arreguín
Subdirector General Técnico
Comisión Nacional del Agua
Insurgentes Sur 2416, piso 8, colonia Copilco el Bajo
04340 México, D.F., México
Teléfonos: +52 (55) 5174 4401 y 5174 4400, extensión 1620
Fax: +52 (55) 5174 4402
felipe.arreguin@conagua.gob.mx
M.I. Ignacio Romero
Subjefe de Disciplina
Subgerencia de Proyectos Hidroeléctricos
Comisión Federal de Electricidad
Río Mississippi 71, colonia Cuauhtémoc
06500 México, D.F., México
Teléfono: +52 (55) 5229 4400, extensión 61149
ignacio.romero02@cfe.gob.mx
irc_unam@yahoo.com.mx
Resumen
Este artículo presenta el procedimiento y la aplicación de análisis de confiabilidad con diversos métodos en un problema sencillo, como es la capacidad de descarga de una alcantarilla. En el análisis se considera que las tres variables de rugosidad, diámetro y pendiente poseen distribuciones de probabilidad normales y se aplican para efectos de comparación los métodos de integración directa; el de Monte Carlo; el de la transformada de Mellin, con la estimación de primer orden de la variancia; el método de Rosenblueth y de Harr del punto de estimación; el método del primer orden del segundo momento estadístico (MFOSM), y el método avanzado del primer orden del segundo momento estadístico (AFOSM), con dos versiones: el de Hasofer-Lind y el de Tang. Se adopta como verdadero el resultado de la probabilidad de falla obtenida con el método de integración directa (lo cual no es posible en análisis complejos, sobre todo cuando las incertidumbres sean importantes) y se comparan los resultados. La mayoría de los métodos puede aplicarse y es posible obtener estimaciones confiables cuando los métodos se aproximan a comportamientos lineales, pero cuando se tiene no linealidad de las variables o bien cuando las incertidumbres se incrementan significativamente, la precisión de algunos métodos se deteriora rápidamente. Tal es el caso del método del primer orden del segundo momento estadístico. Para métodos con muestras de gran tamaño en sus variables, el método de Monte Carlo es el de mayor aplicación, pero la confiabilidad del método converge cuando se tiene un gran número de simulaciones y no se conoce estrictamente el resultado final de la probabilidad de falla; otra limitante importante es que el número de variables puede hacer que el problema no tenga una solución práctica. Métodos en los que se emplea el punto de estimación (Rosenblueth y Harr) pueden ser muy atractivos desde el punto de vista computacional, en la medida en que el número de variables se incrementa y pueden parecer muy buenos en su empleo, ya que ofrecen resultados parecidos a los obtenidos con el método de Monte Carlo y el de integración directa; sin embargo, en caso de que las incertidumbres sean importantes, pueden existir diferencias significativas. El método del primer orden del segundo momento estadístico es aplicable sólo en casos muy sencillos en los que la función de comportamiento está claramente definida y existe una linealidad en las variables; empero, en problemas complejos pierde precisión rápidamente. El método del primer orden del segundo momento estadístico es muy aplicable y puede tomar en cuenta incertidumbres en caso de que el analista decida hacer correlaciones de las variables que intervienen en el problema y que la mayor parte de las veces se asocian con incertidumbres; ésta parece ser una gran ventaja sobre los demás métodos, ya que es posible involucrar variables que en muchas ocasiones se ignoran o deprecian por no poder analizarlas. El método de Hasofer en problemas simples parece ser bastante apropiado; sin embargo, el método de Tang resulta muy atractivo, al analizar el estado límite de falla del problema estudiado.
Palabras clave: evaluación de riesgos, incertidumbre, confiabilidad.
Abstract
This article presents the procedure and application of several methods of risk and reliability analysis to a simple problem, such as the discharge capacity of a sewer. The analysis considers that the three variables of roughness, diameter, and slope have normal probability distributions and are applied for comparing direct integration methods; the Monte Carlo Method; Mellin Transform, with first-order variance estimation; Rosenblueth's and Harr's Point Estimation Method; the First Order Second Moment Method (MFOSM); and two versions of the Advanced First Order Second Moment Method (AFOSM): Hasofer-Lind's and Tang's. The result of the probability of failure obtained with the direct integration method is taken as true (which is not possible in complex analyses, especially when uncertainties are significant) and results are compared. Most methods can be applied, and it is possible to obtain reliable estimations when the methods come close to linear behaviors, but when the variables are not linear or when uncertainties increase significantly, the accuracy of some methods deteriorates rapidly. Such is the case of the MFOSM method. For methods with samples with sizeable variables, the Monte Carlo method is the most commonly applied, but the reliability of the method converges when there is a large number of simulations, and the final result of the probability of failure is strictly unknown; another important limitation is that the number of variables may cause the problem not to have a practical solution. Methods where point estimation is used (Rosenblueth and Harr) may be very attractive from a computational perspective in as much as the number of variables increases and may seem to be good to use, since they offer similar results to those obtained with the Monte Carlo method and the direct integration method. However, if uncertainties are significant, there may be meaningful differences. The MFOSM method is applicable only in very simple cases where the behavior function is clearly defined and there is variable linearity; however, it rapidly looses accuracy in complex problems. The MFOSM method is quite applicable and can take into account uncertainties in case the analyst decides to make correlations of the variables that intervene in the problem and that most of the times are associated with uncertainties. This seems to be a great advantage over the other methods, since it is possible to involve variables that are many times ignored or undervalued because they cannot be analyzed. The Hasofer Method seems to be quite appropriate for simple problems; however, the Tang Method is quite attractive for analyzing the failure limit state of the problem studied.
Keywords: risk assessment, uncertainty, reliability.
Introducción
El diseño y análisis de la ingeniería de recursos hidráulicos trata con la ocurrencia del agua en varios sistemas y sus efectos en diversos aspectos, tales como el ambiente, la ecología y lo relativo a la sociedad.
Debido a la naturaleza extremadamente compleja de los procesos físicos, químicos, biológicos y sociales, se han realizado enormes esfuerzos por diversos investigadores para tratar de tener un mejor entendimiento de los mismos. Un producto benéfico de estos estudios de investigación ha sido el desarrollo de modelos que describen la interrelación e interacción que tienen cada una de las componentes de dichos procesos, lo cual se pretende en este artículo. El término "modelo" se refiere a cualquier elemento estructural y no estructural de transformación que produce alguna clase de efecto en la salida de los modelos mencionados.
En la ingeniería de los recursos hidráulicos, la mayoría de los modelos son estructurales y toman la forma de modelos matemáticos, ecuaciones, cuadros, gráficas o programas de computadora. El modelo es una herramienta útil para los ingenieros, que les permite predecir el comportamiento del sistema ante varios escenarios posibles en los que la eficiencia y efectividad del modelo puede formular dicho comportamiento. Aun así, se debe hacer un mayor esfuerzo para mejorar nuestro entendimiento de los procesos que intervienen en los sistemas hidráulicos y acotar las incertidumbres que se tienen acerca de las variables que aparecen en dichos modelos.
En general, la incertidumbre debida a procesos aleatorios estocásticos no puede ser eliminada, pero puede reducirse a través de un manejo cuidadoso en la recolección y el manejo de los datos que intervienen en los diversos procesos analizados.
Las incertidumbres que intervienen en sus diversos procesos se dividen básicamente en cuatro categorías: hidrológicas, hidráulicas, estructurales y económicas. Más específicamente, en los análisis y diseños se tienen como origen de las incertidumbres las naturales, las inherentes a los propios modelos, las asociadas con los datos y las operacionales.
Las naturales están asociadas con su propia naturaleza aleatoria, tales como la ocurrencia de precipitaciones y avenidas; los eventos hidrológicos tienen variación en el tiempo y el espacio, y su naturaleza no puede ser predicha con exactitud. Debido a lo anterior, el modelo no es más que una abstracción de la realidad, que generalmente involucra simplificaciones e idealizaciones. La incertidumbre de los modelos refleja la discrepancia que se tiene entre la realidad y el modelo. Las incertidumbres paramétricas son el resultado del manejo de datos que miden los fenómenos; también pueden tener el efecto de la recolección propia de los mismos y, en ocasiones, de cambios operacionales que afectan la correcta interpretación de los datos.
Las incertidumbres en los datos pueden deberse a (1) errores de medición, (2) inconsistencia y no homogeneidad de los mismos, (3) errores en el manejo y la transcripción y (4) una inadecuada representación de las muestras analizadas.
En general, las incertidumbres operacionales incluyen aquellas asociadas con la construcción, manufactura, deterioro, deficiencias en el mantenimiento y, en muchas ocasiones, el error humano. La magnitud de este tipo de incertidumbres depende fundamentalmente de la correcta operación de los sistemas y del control de calidad adecuado en la construcción y fabricación de los equipos con los que se operan los sistemas. El deterioro progresivo debido a la falta de un mantenimiento adecuado puede resultar en cambios importantes en la resistencia y en ocasiones en una disminución de la capacidad estructural, lo cual debe merecer un especial cuidado en el proceso de análisis de diversos sistemas de ingeniería en el futuro.
El objetivo de este artículo es mostrar el estado del arte de cómo evaluar las incertidumbres y la confiabilidad en los proyectos hidráulicos de ingeniería, con la aplicación a un problema sencillo, como es la capacidad de una alcantarilla.
Técnicas para análisis de incertidumbres
Hay varias técnicas con diversos métodos analíticos que permiten la derivación exacta de las distribuciones de probabilidad acumulada (DPA) o de los momentos estadísticos de variables aleatorias como una función de varias variables aleatorias.
Sin embargo, el éxito de su implementación depende fuertemente de la relación funcional, formas de la DPA estudiada y herramientas matemáticas aplicadas.
Los métodos analíticos son herramientas poderosas en problemas sencillos, aunque su utilidad se limita en los problemas complejos de la vida práctica (real). Las situaciones que existen en los que las técnicas analíticas pueden aplicarse para obtener incertidumbres de modelos de salida con derivaciones analíticas es virtualmente imposible; sin embargo, es práctico entonces encontrar una solución numérica aproximada.
La evaluación de incertidumbres y sus parámetros básicos, media y desviación estándar (dos primeros momentos) es fundamental, debido a la necesidad de conocer con exactitud estos valores, que permitirán determinar la confiabilidad del sistema de ingeniería analizado.
Métodos para evaluar riesgos
a) Método del periodo de retorno
El método del periodo de retorno es un procedimiento tradicionalmente empleado en sistemas de ingeniería asociados con eventos como los hidrológicos y sismológicos, donde los fenómenos que producen las cargas o demandas son variables aleatorias producidas por fenómenos naturales a lo largo del tiempo y entonces se asocia el concepto de ocurrencia o recurrencia. De esta manera se fija un periodo de retorno de diseño relacionado con eventos tales como avenidas, lluvias o sismos que afectan las presas, vertedores, puentes, alcantarillas, etcétera, obteniéndose un gasto pico o un sismo (aceleración del terreno) de diseño; aunque puede estimarse la probabilidad de falla y la de seguridad, y por tanto la confiabilidad del sistema, los periodos de retorno se asocian con eventos históricos presentados y se extrapolan para estimar el evento de diseño, por lo que su aplicación es muy limitada; sin embargo sigue siendo muy usada en la práctica profesional.
En cuanto al método del periodo de retorno, Wood (1977) estimó los riesgos al evaluarlos con un método de transformación integral; Duckstein y Borgardi (1981) consideraron factores de incertidumbre para integrar la unión de la función de densidad de probabilidad de "resistencia y carga", para evaluar la probabilidad de la falla de un sistema de presas; Cornell (1969) aplicó el método del valor medio del primer orden del segundo momento estadístico (MFOSM) en la ingeniería de diseño; Tung y Mays (1977) aplicaron el MFOSM para estimar las confiabilidades estáticas y dependientes de tiempo en sistemas de alcantarillado; Wood (1977) expandió la función de comportamiento del punto de falla utilizando series de Taylor, usando el método avanzado de primer orden del segundo momento estadístico (AFOSM); McKay et al. (1979) establecieron el muestreo del hipercubo latino (LHS) para mejorar la convergencia de la función de comportamiento del método de Monte Carlo. Marengo (2006), por su parte, empleó el AFOSM para estimar el riesgo de falla en obras de desvío, en los que comparó la probabilidad de falla obtenida con este método y el del periodo de retorno.
Este periodo de retorno se selecciona por guías y recomendaciones; por ejemplo, la avenida de diseño para la obra de excedencias es de 10 000 años para puentes de 200 o 250 años; para la obra de desvío en cortinas flexibles (tierra y enrocamiento) de 50 a 100 años, y para cortinas de concreto (arco y gravedad) de 10 o 20 años; para el análisis sísmico de la cortina de una presa se considera un sismo de diseño con periodo de retorno de 1 000 a 10 000 años; se estima como sismo más frecuente el asociado con 200 años de periodo de retorno.
El periodo de retorno se define como el tiempo promedio en que una magnitud de la resistencia Y será igualada o excedida (Chow, 1953; Ang et al., 1991). Por lo anterior, si Tr se expresa en años (para Tr > 1), la probabilidad de que un evento Z iguale o exceda a Y en cada año está dado por:

En fenómenos naturales, Z se supone como una variable continua, y si el riesgo de falla se define como la probabilidad de ocurrencia de que Z sea mayor que Y en cada año, entonces la probabilidad de que un sistema no falle es:
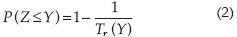
La probabilidad de que no se presente una falla en alguno de los n años de la vida útil del proyecto será:

Cabe mencionar que al desarrollar las ecuaciones (1), (2) y (3) se han hecho dos suposiciones: a) la ocurrencia de los fenómenos de la variable aleatoria Z es independiente en la vida útil de n años, y b) el sistema natural es invariante en el tiempo.
Sin embargo, cuando un sistema hidráulico y, en general una estructura, queda expuesto a variaciones temporales, entonces la probabilidad asociada con el periodo de retorno, como se expresó en las ecuaciones anteriores, tampoco puede usarse como una medida del riesgo de estructuras sujeta a este tipo de acciones (Borgman, 1963).
Aun cuando el riesgo evaluado con la ecuación (3) considera una buena parte de los riesgos por eventos naturales, existen incertidumbres asociadas con las variables que integran las expresiones de carga y resistencia de los sistemas analizados que no se toman en cuenta, por lo que el riesgo total de un sistema complejo en el que intervienen fenómenos naturales no debe evaluarse con otro método.
b) Método de integración directa
El riesgo se evalúa por medio de una integración directa, analítica o numérica de las funciones de densidad de la carga y resistencia. En este caso, las funciones de distribución mencionadas deben estar definidas. Si dichas situaciones describen correctamente las variables que representan, entonces el método es exacto.
En 1980, Tang presentó un procedimiento que permite incorporar las incertidumbres al modelo de probabilidad en la evaluación del riesgo de falla en presas; para ello utilizó una integración directa para la valoración del riesgo hidrológico. En 1977, Wood calculó la sobreelevación y el riesgo estructural en forma analítica, con funciones de densidad de probabilidad supuestas para las avenidas y para los modos de falla, donde no se consideraron las incertidumbres hidrológicas, hidráulicas y de modelación paramétrica. También en 1977, Tung y Mays definieron los riesgos para alcantarillas y bordos, al estimar primero los parámetros estadísticos de carga y resistencia a partir de las incertidumbres de los parámetros con fórmulas de aproximación de primer orden y asignando entonces funciones de distribución a la carga y resistencia.
El riesgo evaluado es sumamente sensible a la función de distribución asignada, por lo que una suposición impropia o una aproximación mal hecha de dichas acciones pueden demeritar la exactitud ganada al hacer la integración directa.
Duckstein y Bogardi, en 1981, también estudiaron el problema de bordos asociados con varios tipos de falla, como sobreelevación, tubificación, deslizamiento de taludes y erosión por viento. El riesgo se estimó con la integración directa de la unión de las funciones de densidad de las variables de carga y resistencia; sin embargo, la selección de la resistencia fue un tanto ambigua y las incertidumbres no se representaron claramente.
La mayor desventaja del método de integración directa es la gran dificultad que se tiene para derivar correctamente las funciones de distribución de probabilidad de las variables de suministro y demanda, especialmente en sistemas complejos, como las presas de tierra y enrocamiento. Asimismo, una vez que las funciones de densidad se establecen, existe una gran dificultad para integrarlas, incluso con la ayuda de computadoras. De esta manera, el método de integración directa es bueno solamente para sistemas simples o cuando se requiere gran exactitud en la evaluación del riesgo y se conocen perfectamente las funciones de densidad de probabilidad de las variables que intervienen en el problema.
c) Método de simulación de Monte Carlo
Es un proceso que utiliza en cada simulación un conjunto particular de valores de variables aleatorias generadas artificialmente de acuerdo con la distribución de probabilidad que se está analizando.
Con cálculos relativamente sencillos, pero repetitivos, se puede encontrar un conjunto de valores con los que se estima la función de distribución de probabilidad del margen de seguridad FM(0). El riesgo de falla se evalúa como la relación entre el número de valores positivos o negativos de FM(0) con respecto al total de elementos generados.
En 1981, Duckstein y Bogardi estimaron la probabilidad de falla en presas de jales (minas). En 1972, Haan evaluó con este método las probabilidades de error en problemas hidrológicos, en función del número de observaciones usadas para la determinación de parámetros de los modelos estocásticos.
En 1975, Matalas et al. aplicaron el método para estimar los parámetros estadísticos de media, desviación estándar y coeficientes de asimetría a varias distribuciones de secuencias de flujo.
Chow, en 1953, utilizó el método para generar secuencias de datos para el estudio del comportamiento de sistemas hidrológicos. En 1977, Wen usó los resultados obtenidos con la simulación de Monte Carlo para verificar la derivación de la estadística de combinaciones de cargas extremas.
Ang et al. (1991) manejaron el método de simulación de Monte Carlo con el llamado muestreo de importancia en casos multidimensionales; Leira (1991) lo aplicó con distribuciones normales multivariadas, e Ibrahim y Rahman (1991) lo usaron para revisar la confiabilidad de sistemas dinámicos con incertidumbre.
Según Hoshiya et al. (1991), dicho muestreo de importancia parte de considerar que la estimación de la probabilidad de falla de diversos sistemas estructurales se hace en un rango tan pequeño (10-5 o 10-6), que la función de densidad de probabilidad es postulada como una función desconocida del tipo exponencial F(Z, α1, α2, ...) en la vecindad de Z = 0, donde α1, α2... son valores constantes a identificarse (generalmente por correlación).
En la medida que el muestreo de Z1 se inicia, se obtiene inmediatamente un grupo de datos experimentales para la función de distribución de Z usando Z1 y se hace un ajuste de los datos con los que se consigue F(Z, α1, α2, ...). Aunque este ajuste es inestable en un principio, en la medida que se procede en el muestreo, el proceso es esencialmente secuencial y se puede llevar a cabo por medio del proceso de filtrado de Kalman, el cual se describe claramente en la referencia de Hoshiya et al.
Cuando αi converge a valores en los que el coeficiente de autocorrelación es cercano a uno, la probabilidad de falla del sistema se estima como:

Cabe subrayar que con este método es posible obtener una convergencia eficiente debido a que el procedimiento es una "aproximación lineal" de PF en lugar de una estimación puntual, como tradicionalmente se hace.
De hecho, puede decirse que la técnica de Monte Carlo es tal vez la única solución técnica a problemas que no pueden resolverse analíticamente debido al comportamiento no lineal o complejo de las relaciones que intervienen en los sistemas analizados. Sin embargo, este método tiene las siguientes desventajas:
1. El riesgo estimado al usar la técnica no es único, depende del tamaño de la muestra y del número de simulaciones. Los momentos estadísticos reales de la unión de funciones de distribuciones de probabilidad no son del todo ciertas.
2. El costo y tiempo de computación que se consume con esta técnica se incrementa sustancialmente en la medida que el nivel de precisión y el número de variables se incrementen; en general, se recomienda que si se puede aplicar un modelo analítico, éste debe preferirse a la simulación de Monte Carlo.
Confiabilidad
La confiabilidad de un sistema de ingeniería "es más realista cuando se mide en términos de la probabilidad" (Tang, 1984). El objetivo de un análisis de confiabilidad (Marengo, 2006) es asegurar durante la vida útil de un proyecto o en el periodo de tiempo en el que es evaluado que X > Y, donde X es la capacidad de resistencia del sistema y Y es la capacidad de demanda (o carga); colocados tanto la demanda como la resistencia en un entorno natural, ambos están sujetos a variabilidad por diversas condiciones de carga externas; es obvio que también la resistencia puede cambiar en el tiempo.
Tradicionalmente en un problema de demanda-resistencia (Marengo, 2006), la confiabilidad se expresa en función del factor de seguridad FS = X/Y o como el margen de seguridad MS = X-Y, mientras que las variables FS, MS, X y Y se consideran determinísticas. Si la resistencia y la demanda tienen naturaleza estocástica, también FS y MS serán variables aleatorias estocásticas.
Cuando un análisis se lleva a cabo con variables estocásticas (Marengo, 2006), los resultados usualmente se expresan en términos del índice de confiabilidad β, al que se le calcula la probabilidad de ocurrencia ps, que en un sistema de ingeniería hidráulica se define como la probabilidad de seguridad (no falla) en el que la resistencia del sistema excede la carga; esto es:

La probabilidad de falla, pf, es el complemento de la confiabilidad o riesgo, que puede expresarse como:

Debe recordarse que el riesgo en un sistema de ingeniería puede estimarse (USACOE, 1976) como:

Donde R = riesgo, Tr = periodo de retorno y n = el periodo de análisis del evento (que usualmente es la vida útil), ya que es posible asociar la probabilidad de ocurrencia con el periodo de retorno (ecuación (3)); entonces, cuando se emplea este criterio, el riesgo se expresa como:

Hay dos enfoques básicos probabilísticos para evaluar la confiabilidad de un sistema de ingeniería hidráulica. El enfoque más directo es un análisis estadístico de los datos de los últimos registros de falla para sistemas similares. El otro enfoque es a través del análisis de confiabilidad, que considera y combina la contribución de cada factor que potencialmente influye en la falla. El primero es un enfoque de sistema "lumped", en el que no hay necesidad de ningún conocimiento sobre el comportamiento de la historicidad de la estructura ni su carga ni su resistencia. Por ejemplo, los datos de falla por desbordamiento en presas revelan que el mayor valor promedio ocurre para presas entre 15 y 30 m de altura, con un 50.82% de los casos (21 de 61 casos de fallas totales) (Marengo, 1996) y la probabilidad de falla para presas construidas en nuestros días es alrededor de 10-5 por presa por año (Marengo, 1996). En muchos casos, este enfoque directo no es práctico, porque (a) el tamaño de la muestra es demasiado pequeño para ser estadísticamente confiable, especialmente para la baja probabilidad de consecuencia de eventos; (b) la muestra puede no ser representativo de la estructura o de la población, o de grupos específicos de la misma; y (c) las condiciones físicas de la presa pueden ser no estacionarias, es decir, que varían con respecto al tiempo. El riesgo promedio de falla de presa antes mencionado sólo considera los casos de falla totales y no distingue presas viejas de nuevas presas, en las que las prácticas de seguridad reducirán seguramente el riesgo de falla; tampoco distingue el tipo de falla que se está analizando.
Hay dos pasos importantes en el análisis de confiabilidad: (a) identificar y analizar la incertidumbre de contribución de cada factor y (b) combinar las incertidumbres de los factores estocásticos para determinar la confiabilidad general de la estructura. El segundo paso, a su vez, podrá proceder de dos maneras: (1) directamente, combinando las incertidumbres de todos los factores o (2) separadamente, al combinar las incertidumbres de los factores pertenecientes a diferentes componentes o subsistemas para evaluar primero la confiabilidad de subsistema respectivos y, a continuación, combinando las confiabilidades de los diferentes componentes o subsistemas a ceder la capacidad de confiabilidad global de la estructura. La primera forma se aplica a estructuras muy simples, mientras que la segunda es más conveniente para sistemas complicados. Por ejemplo, para evaluar la confiabilidad de una presa, las confiabilidades asociadas con la hidrología, hidráulica, geotecnia, estructuras y otras disciplinas, podrían evaluarse por separado primero y, a continuación, se combinan para encontrar la confiabilidad general. O bien, de los componentes, podían ser evaluadas en primer lugar, según los diferentes modos de falla y, a continuación, combinarlos. Vrijling (1993) proporciona un ejemplo real de la determinación y combinación de las confiabilidades de las componentes en el diseño de la barrera que surge de tormentas en la zona oriental de Holanda.
En esta sección se describen varios métodos analíticos que permitirían una derivación exacta de la DPA y/o momentos estadísticos de una variable aleatoria como una función de varias variables aleatorias. El éxito de la implementación de estos procedimientos depende en gran medida de la relación funcional, las formas de las DPAs involucradas y la habilidad matemática del analista. Los métodos analíticos son potentes herramientas para problemas que no son demasiado complejos.
a) Técnica analítica: "Transformada de Mellin"
Cuando las variables aleatorias en una función W = g(X) son independientes y no negativas, y g(X) tiene una forma multiplicativa como:

la transformada de Mellin es especialmente atractiva para realizar análisis de incertidumbre (Tung, 1990). Para una función con DPA fX(x), donde x es positiva, se define como:

Donde MX(s) es la transformada de Mellin de la función fX(x) (Springer 1979). Por lo tanto, la transformada de Mellin proporciona una forma alternativa para encontrar los momentos de cualquier orden para variables aleatorias no negativas.
Al igual que la propiedad de convolución de las transformadas Exponencial y de Fourier, la transformada de Mellin de la convolución de las DPA asociadas con múltiples variables aleatorias independientes en una forma de producto es simplemente igual al producto de las transformadas de Mellin de las DPA individuales. Además de la propiedad de convolución, la transformada de Mellin tiene varias propiedades operacionales útiles, como se muestra en el anexo I.
b) Técnica aproximación: método de estimación de primer orden de la variancia (FOVE)
Este método es llamado también método de la propagación de la variancia. Estima incertidumbres en un modelo que se basa en propiedades estadísticas de modelos de variables aleatorias. La idea básica del método es aproximar un modelo que involucra variables aleatorias por medio de la expansión de series de Taylor.
Considerando que una función hidráulica o hidrológica W está relacionada con N aleatorias X1, X2,...XN como:

Donde X = (X1, X2, XN)t es un vector columna N dimensional de variables aleatorias y t = representa la matriz transpuesta.
La expansión de la serie de Taylor de la función g(X) con respecto a las medias de las variables aleatorias de X = μ en el espacio puede expresarse como:

Donde μi es la media de las variables Xi, μj. es la media de las variables Xj y ε representa los términos de orden superior.
Las derivadas parciales de primer orden son los llamados coeficiente de sensibilidad y cada uno representa la razón de cambio en el modelo W con respecto a la unidad de cambio de cada variable en μ.
Despreciando los términos de orden superior (ε en la ecuación (12)), la esperanza del modelo W puede expresarse como:
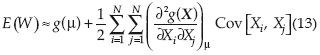
Y la variancia de W = g(X) puede expresarse como:

Cuando las variables aleatorias están correlacionadas, la estimación de la variancia W, usando la aproximación de segundo orden, requeriría del conocimiento del producto de momentos cruzados entre las variables correlacionadas. En la práctica, esta información raramente está disponible; cuando las variables son independientes, las ecuaciones (13) y (14) pueden plantearse como:
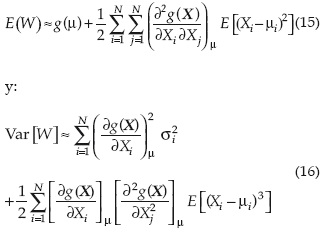
En esta ecuación (16), la variancia de W, a partir de la aproximación de segundo orden, bajo la condición de que todas las variables son estadísticamente independientes, requeriría del conocimiento del tercer momento.
En las aplicaciones prácticas, donde los momentos de orden superior y los productos cruzados de los momentos no están disponibles fácilmente, la aproximación de primer orden frecuentemente se adopta.
Al truncar los términos de segundo orden y mayores en la serie de Taylor, la aproximación de primer orden de W en X = μ es:

En la cual s =∇x W(μ) es un vector columna N-dimensional de coeficientes de sensibilidad evaluados en el punto de falla; C(X) es la matriz de variancia-covariancia del vector aleatorio X. Cuando todas las variables aleatorias son independientes, la variancia del modelo W de salida puede aproximarse como:
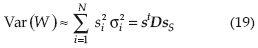
En la que σ representa la desviación estándar y D = diag(σ12, σ22, ..., σn2) es una matriz diagonal que involucra las variancias de las variables aletorias. De la ecuación (19), la relación 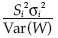 indica la proporción de la incertidumbre en el modelo de salida que contribuye con la incertidumbre de la variable aleatoria Xi.
indica la proporción de la incertidumbre en el modelo de salida que contribuye con la incertidumbre de la variable aleatoria Xi.
c) Técnica aproximada: método de Rosenblueth del método de estimación probabilística (EP)
El método de estimación de aproximación probabilística de Rosenblueth (EP) es una técnica computacional directa que permite hacer un análisis de incertidumbre. Se puede usar para estimar estadísticamente momentos de cualquier orden, en un modelo que involucra varias variables aleatorias correlacionadas o no.
Originalmente, el método de Rosenblueth fue desarrollado para usarse con variables sintéticas (Rosenblueth, 1975). Posteriormente se extendió para el tratamiento de variables no sintéticas (Rosenblueth, 1981).
Considérese un modelo W = g(X) que involucra una variable aleatoria simple "X", cuyos tres primeros momentos o la función de densidad de probabilidad o la función de distribución de probabilidad son conocidas.
En relación con la figura 1, el método de estimación probabilística de Rosenblueth (EP) se aproxima a la función de distribución de probabilidad de la variable "X", al suponer que la masa de la distribución de probabilidad de "X" se concentra en dos puntos x- y x+. Usando los dos puntos de aproximación, las ubicaciones de x- y x+, y las masas correspondientes p- y p+, se determinan para preservar los tres primeros momentos de la variable X. Sin cambiar la naturaleza del problema original, es más fácil tratar con la variable estandarizada la cual tiene media cero y variancia unitaria. Por lo tanto, en términos de x'-, x'+, p- y p+:
la cual tiene media cero y variancia unitaria. Por lo tanto, en términos de x'-, x'+, p- y p+:


En estas ecuaciones,  y γ es el coeficiente de asimetría de la variable aleatoria "X". Resolviendo las ecuaciones (20) a (23) en forma simultánea se obtiene:
y γ es el coeficiente de asimetría de la variable aleatoria "X". Resolviendo las ecuaciones (20) a (23) en forma simultánea se obtiene:

Cuando la distribución de la variable aleatoria "x" es simétrica, es decir, cuando γ = 0, entonces las ecuaciones (24) a (27) se reducen a x'-= x'+ = 1 y p- = p_= 0.5. Esto implica que para una variable simétrica aleatoria, los dos puntos están localizados a cada lado de la desviación estándar de la media, con igual probabilidad de masa en los dos puntos.
A partir de x'- y x'+, los dos puntos en el parámetro original de espacio x- y x+ pueden determinarse respectivamente como:
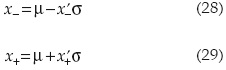
Basado en x- y x+, los valores del modelo W = g(X) en los dos puntos pueden calcularse como: w-= g(x-) y w+ = g(x+).
Entonces, los momentos alrededor del origen de W = g(X) de cualquier orden pueden estimarse como:

Además del método de la estimación de primer orden de la variancia (FOVE), el método de la estimación probabilística (EP) de Rosenblueth provee una capacidad adicional que permite hacer el análisis que toma en cuenta la asimetría asociada con la función de distribución de probabilidad (DPA) de una variable aleatoria. Karmeshu y Lara-Rosano (1987) demuestran que el método de FOVE es una aproximación de primer orden del método de Rosenblueth de estimación probabilística.
Es un caso general donde el modelo involucra N variables. El nésimo momento de salida W = g(X1, X2,..., Xn) alrededor del origen puede aproximarse como:

En la que el signo del indicador con subíndice δi puede ser sólo + o -, representando la variable aleatoria, xi, teniendo el valor de:

Respectivamente, la probabilidad de masa en cada uno de los 2N puntos, p(δ1, δ2,..., δN) puede aproximarse como:
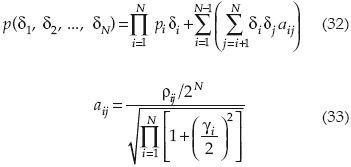
Donde ρij es el coeficiente de correlación entre las variables aleatorias xi y xj. El número de términos entre la sumatoria de la ecuación (32) es 2N, que corresponde al número total de posibles combinaciones de + y - para todas las N variables aleatorias.
d) Método de aproximación probabilística de Harr. Método del punto de estimación
Para evitar la intensiva naturaleza computacional del método de estimación probabilística de Rosenblueth cuando el número de variables aleatorias es relativamente grande, Harr (1989) propuso un método probabilístico alterno que reduce el número de evaluaciones requeridas de 2N a 2N y amplía significativamente el método de estimación probabilístico a un análisis probabilístico de problemas prácticos.
El método se aplica al segundo momento estadístico y es capaz de tomar en cuenta los dos primeros momentos (media y variancia) de las variables aleatorias involucradas y sus correlaciones. Los coeficientes de sesgo de las variables correlacionadas se ignoran en el método. Las bases teóricas del método de Harr se basan en transformaciones ortogonales de la matriz de correlación.
La transformación ortogonal es una herramienta importante para tratar problemas con variables aleatorias correlacionadas. El objetivo principal de la transformación es mapear las variables correlacionadas de su espacio original a un nuevo dominio, en el cual no están correlacionadas, por lo que el análisis se simplifica significativamente.
Considérese N variables aleatorias multi-variadas X=(X1, X2, Xn)t que tienen asociadas un vector de valores medios:
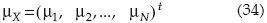
Y una matriz de correlación R(X):
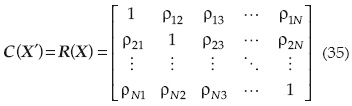
Nótese que la matriz de correlación es simétrica; esto es: ρij= ρji para i ≠ j.
La transformación ortogonal puede hacerse usando la descomposición de los eigen valores o también llamada descomposición espectral, en la que R(X) se descompone como:
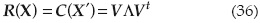
Donde V en una matriz de tamaño NxN, que contiene N eigen vectores como V = (υ1, υ2,..., υN), considerando que Vi es la iésima columna de los eigen vectores y que Λ=diag(λ1, λ2,..., λN) es una matriz diagonal compuesta de eigen valores.
En términos de los eigen vectores y los eigen valores, el vector aleatorio en el espacio paramétrico original puede expresarse como:

En la que Y es un vector de N variables estandarizadas normales, que tiene a D como vector medio y la matriz identidad I, como la matriz de covariancia, y D es una matriz diagonal de variancias de N variables aleatorias.
Las variables transformadas Y son funciones lineales de las variables originales aleatorias, por lo que las variables aleatorias X están normalmente distribuidas; entonces las variables aleatorias se transforman en Y, variables aleatorias estandarizadas normales.
Para un modelo multivariado W = g(X1, X2,... , XN), en el que se involucran N variables aleatorias, el método de Harr selecciona los puntos de evaluación localizados en las intersecciones de ejes de los N eigen vectores localizados en la superficie de una hiperesfera multidimensional, que tiene radio √N en el eigen espacio y se calcula como:

En la que Xi± representa al vector de coordenadas de las N variables aleatorias en el espacio paramétrico, que corresponde al iésimo eigen vector Vi, μ = μ1, μ2..., μN)t , un vector de medias de N variables aleatorias X.
Basado en los 2N puntos determinados por la ecuación (38), se pueden calcular los valores de la función. Entonces el momento nésimo del modelo de salida W alrededor del origen puede calcularse con las siguientes ecuaciones:
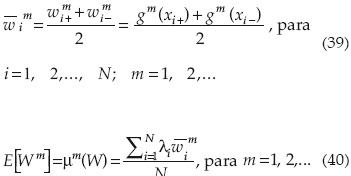
Alternativamente, la transformación ortogonal puede hacerse con la matriz de covariancias.
e) Método del valor medio del primer orden del segundo momento (MFOSM)
En el método del primer orden del segundo momento estadístico, la función de comportamiento, W(X), definida con base en las funciones de carga y resistencia, se expanden en series de Taylor en un punto dado de referencia. A partir del segundo término de la serie se trunca, resultando en una aproximación que requiere del conocimiento de los dos primeros momentos estadísticos de las variables aleatorias. Esta simplificación aumenta considerablemente la practicidad del método de primer orden, porque en muchos problemas reales es muy difícil, si no imposible, encontrar la DPA de las variables que intervienen en los problemas; sin embargo, es muy fácil obtener los dos primeros momentos estadísticos de dichas variables. Los procedimientos para estimar el método de primer orden del segundo momento estadístico se muestran con detalle en la literatura especializada que describe el método FOVE para el análisis de incertidumbres.
Una vez que se han estimado la media y la desviación estándar de W(X), la confiabilidad se expresa como:
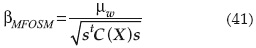
Dónde μ y C(X) son los vectores de medias y matriz de covariancia de las variables aleatorias X, respectivamente; s=∇xW(μ) es el vector columna de los coeficientes de sensibilidad de cada elemento que es evaluado en X = μ.
f) Aproximación de primer orden de la función de comportamiento en el punto de diseño, método avanzado del primer orden del segundo momento (AFOSM), según Hasofer-Lind
La principal ventaja del método AFOSM es tratar de mitigar las deficiencias asociadas con el método del primero orden del segundo momento estadístico (MFOSM) anterior, pero conservando la simplicidad de la aproximación del primer orden; es decir, calculando sólo los dos primeros momentos estadísticos de las variables estudiadas. La diferencia entre el MFOSM y el AFOSM es que el punto de expansión de primer orden en este último está localizado en la superficie de falla y el primero en el punto medio de las variables estandarizadas, por lo que los investigadores que estudian estos temas recientemente prefieren el método avanzado en lugar del método de primer orden.
Considerando el punto de expansión en X0 = X*:
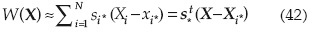
En la que s* = (s1* s2*,...sN*)t es un vector de sensibilidad de los coeficientes de la función de comportamiento W(X) evaluado en el punto de expansión X*.
El valor de S es:

Entonces el valor medio y la variancia de la función W(X) pueden expresarse como:
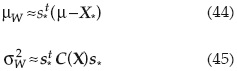
En la que C(X) es la matriz de covariancias de las variables aleatorias; si las variables no están correlacionadas:

La desviación estándar de la función de comportamiento W(X) puede expresarse en términos de las derivadas direccionales como:
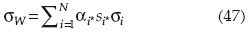
Donde αi, es la derivada direccional para la variable iésima en el punto x*:
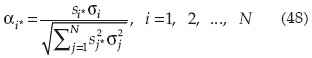
En forma matricial:

El índice de confiabilidad se estima entonces como:

Una vez que βAFOSM se ha calculado, la confiabilidad puede estimarse como ps = Φ(βAFOSM); la sensibilidad de las variables se calcula como:

Ecuación que muestra que -αi* es la relación del cambio en βAFOSM debido a un cambio en la desviación estándar de la variable Xi en X = X*. Entonces la relación entre ∇x'β y ∇xβ puede expresarse como:

También puede demostrarse que el coeficiente de sensibilidad de la confiabilidad o probabilidad de falla con respecto a cada variable estocástica puede ser expresada como:
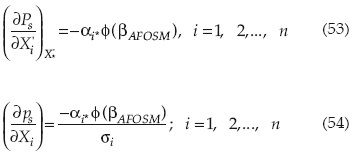
En forma matricial:

El coeficiente de sensibilidad muestra la importancia relativa de cada variable estocástica en la confiabilidad o probabilidad de falla.
El algoritmo del método avanzado del segundo momento para variables independientes según Hasofer y Lind (AFOSM) es el siguiente:
Si X son variables normales independientes, la estandarización se reduce a Z variables con media cero y matriz de covariancia I, siendo I una matriz de identidad NxN. Hasofer propuso la ecuación recursiva:
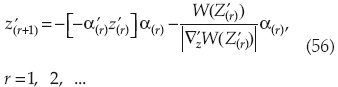
Donde:
ri es la iteración iésima.
α es el vector unitario de la superficie de falla.
En el espacio, x se escribe:
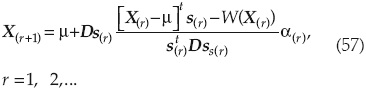
Basado en esta ecuación, el algoritmo de Hasofer-Lind con el método AFOSM queda como sigue:
1. Elegir una solución de prueba X(r).
2. Calcular W(X(r)) y el correspondiente vector s(r).
3. Revisar el punto de solución X(r+1) de acuerdo con la ecuación (57).
4. Verificar si X(r) y X(r+1) son lo suficientemente cercanos; en caso afirmativo, calcular βAFOSM con la ecuación:
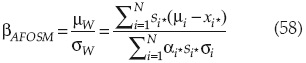
Y el índice de confiabilidad Ps = φ(βAFOSM)
Si X(r) ≠ X(r+1) entonces repetir 2; en caso contrario:
5. Calcular el índice de confiabilidad con respecto a los cambios de las variables estocásticas.
Debido a la naturaleza no lineal de la optimización, el algoritmo anterior no converge necesariamente en el verdadero punto de diseño asociado con el mínimo índice de confiabilidad, por lo que Tang propuso un método que lo vuelve convergente a dicho punto de diseño.
g) Método avanzado del primer orden del segundo momento estadístico según Tang
La formulación matemática del método del primer orden del segundo momento estadístico se muestra con detalle en el libro de Tang (1980); sin embargo, a continuación se presentan las bases de la formulación matemática y un resumen de su aplicación.
Los conceptos relativos a confiabilidad pueden limitarse a una formulación basada en el primero y segundo momentos estadísticos de las variables aleatorias que intervienen en el problema de la formulación del segundo de ellos (Cornell, 1969; Ang y Cornell, 1974).
Con el enfoque del segundo momento, la confiabilidad puede medirse completamente en función del primer y segundo momento de las variables de diseño.
Tomando en cuenta que la definición de margen de seguridad es M = X - Y, el "estado de seguridad" se define para M > 0 y el "estado de falla" para M < 0. La frontera que separa los estados de falla y seguridad queda establecida para M = 0. Si se consideran las variables reducidas:

El espacio de estas variables reducidas se muestra en la figura 2. También en términos de las variables reducidas, la ecuación límite M = 0 viene a ser:


que es la línea recta mostrada en la figura 2. La distancia desde la línea de falla al origen 0 está dada por:
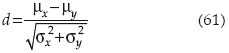
Esta expresión se cumple solamente si las funciones de distribución de probabilidad de las variables analizadas son normales y no están correlacionadas entre sí.
Lo anterior sucede porque sólo con la distribución normal, en el caso de variables no correlacionadas, se cumple que la media de la suma de las variables que intervienen en el problema es la suma de las medias de la función de comportamiento; lo mismo se aplica al hecho de que en este caso la variancia de la función de comportamiento es la suma de las variancias de las variables estudiadas.
Debido a lo anterior, en el caso de que se tengan variables con distribuciones de probabilidad diferentes a la normal, se debe evaluar la probabilidad que corresponde con base en la distribución normal equivalente, cuya aplicación se muestra en diversos libros de estadística.
Ya que la distancia mínima puede interpretarse como una medida de la confiabilidad del sistema, entonces la evaluación de la ecuación (61) en el origen de las variables reducidas (M' = 0) al tratarse con distribuciones normales puede hacerse de la siguiente manera si:

En el origen de M'(M' = 0), para M = 0 (distancia entre el origen y el estado de falla según la figura 2) conduce a que:

El índice de confiabilidad β es esta distancia mínima al origen (μM/ σM), o sea que:
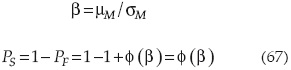
Esta demostración hecha para dos variables (X y Y) en el plano puede generalizarse a tres dimensiones o al espacio de n variables no lineales, al encontrarse un plano tangente a la superficie de falla y la distancia de éste al origen.
Los resultados relevantes de la formulación del método avanzado de primer orden de los segundos momentos pueden resumirse como sigue:
• El punto más probable de falla se puede calcular con la ecuación:

en la cual αi son las direcciones de los cosenos directores:
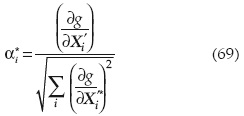
donde las derivadas son evaluadas en (X1'*, X2'*,..., Xn'*), con:
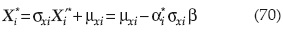
• La solución de la ecuación límite de estado permite obtener β.
Los resultados resumidos anteriormente permiten plantear el siguiente algoritmo para aplicar el método avanzado de primer orden de los segundos momentos estadísticos, y que es el empleado en el cuerpo del trabajo:
1. Definir una función de comportamiento "g(X)" con las variables estadísticas que se consideren adecuadas y significativas en el problema analizado.
2. Suponer un punto inicial de falla X'i*; i = 1, 2, ...,..., n y obtener:
3. Estimar (∂g/∂X'i*) y αi* en los puntos xi*.
4. Calcular xi* con: X1* = μxi - αi* σxi β.
5. Sustituir los valores estimados de Xi* en la función de comportamiento y encontrar β.
6. Con el valor de β obtenido reevaluar X'i* = - αiβ.
7. Repetir los pasos tres a seis hasta que se obtenga la convergencia deseada que sucede cuando βi ≅ βi+1.
Debe señalarse que con la aplicación de este método no es posible estimar el valor medio de la función en conjunto debido a la naturaleza no lineal de la aplicación del método.
Aplicación
Para mostrar la aplicación de los métodos indicados se busca determinar la confiabilidad para poder compararlas entre sí.
Una alcantarilla trabaja, utilizando la ecuación de Manning, con las siguientes condiciones (Mays y Tung, 1992):
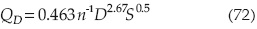
Donde:
Q = gasto en ft3/s.
n = coeficiente de rugosidad en ft1/6.
D = diámetro en ft.
S = pendiente del tubo.
Las propiedades estadísticas de las variables se muestran en el cuadro 1.

La confiabilidad debe calcularse para conocer las condiciones en las que la alcantarilla descargue 35 ft3/ s.
Método de la integración directa
Para la alcantarilla analizada, con variables aleatorias n, D y S, se tienen las siguientes propiedades estadísticas (cuadro 1).
La función de resistencia es:

Y la función de carga es L = 35

Considerando que las variables n, D y S son independientes y lognormales, la función de comportamiento puede escribirse:
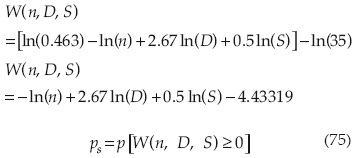
n, D y S son variables lognormales independientes; debido a que ln(n), ln(D) y ln(S) son variables aleatorias independientes, entonces la función de comportamiento W(n, D y S) es una función lineal de variables aleatorias independientes; entonces W(n, D y S) es una función lineal de variables aleatorias normales independientes, cuya media, de acuerdo con la propiedad reproductiva de variables aleatorias es:

Y variancia:

La confiabilidad se puede obtener como:

Método de Monte Carlo
Una vez que se establece la función de comportamiento respectiva (ecuación (73)), se genera una muestra significativa de números aleatorios de cada variable y se estima cuántas veces excede el valor cero; el riesgo de falla se evalúa como la relación entre el número de valores positivos o negativos de FM(0) con respecto al total de elementos generados.
Se adoptaron las características estadísticas de media y desviación estándar para cada variable, con distribuciones de probabilidad normal para cada una de ellas, y se generaron 3 000, 4 000, 5 000 y 6 000 números aleatorios, con una distribución de probabilidad uniforme en un rango U(0,1), obteniendo como resultado para cuatro corridas diferentes los resultados mostrados en el cuadro 2.
Para el análisis se adoptó como resultado el obtenido para 6 000 números aleatorios, que dio como resultado una probabilidad de falla:
pF = 0.02011
Como se señaló anteriormente, el método de Monte Carlo es sensible al tamaño de la muestra y aún con un gran número de simulaciones, en cada caso se obtienen resultados diferentes.
Método de Mellin
En el ejemplo de aplicación considere que los tres parámetros del modelo son variables aleatorias independientes con las propiedades indicadas en el cuadro 3.
De acuerdo con la transformación de Mellin, el gasto MQ(s) puede obtenerse como:

Para el coeficiente de rugosidad n, teniendo distribución uniforme, se obtiene:
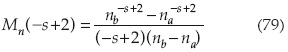
Para el diámetro de la alcantarilla con una distribución triangular se obtiene:
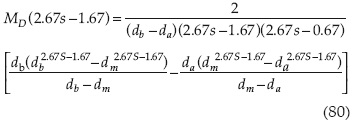
Para la pendiente de la alcantarilla S con distribución uniforme se obtiene:
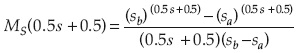
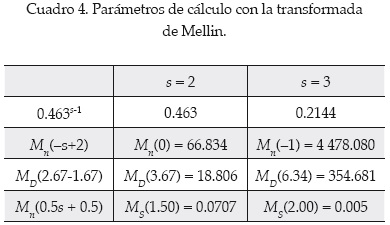
Basado en el anexo I, la transformada de Mellin para cada parámetro del modelo estocástico se puede expresar como se resume en el cuadro 4.
El valor medio de la capacidad de la alcantarilla puede determinarse como:

El segundo momento sobre la capacidad original de la alcantarilla es:

La variancia de la capacidad de la alcantarilla puede determinarse como:

Siendo la desviación estándar:

La media y desviación estándar de la función de comportamiento W son, respectivamente:
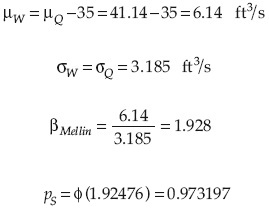
La probabilidad de falla es:
pf = 1-pS = 0.0268
Técnica aproximación: método de estimación de primer orden de la variancia (FOVE)
Suponiendo que las variables no están correlacionas entre sí, la expansión en series de Taylor de la función de comportamiento alrededor de n, μn = 0.015, D, μD = 3.00 y S, μS = 0.005, es:

Tomando en cuenta la ecuación (17), la aproximación de la media de la capacidad del flujo es:
μw ≈ 40.96 ft3/s
De acuerdo con la ecuación (18), la aproximación de la variancia de la capacidad del flujo es:

Esta expresión se reduce a:

Debido a que Cov(n, S) = Cov (D, S) = Cov(n, D) = 0.
Como las desviaciones estándar de la rugosidad, diámetro del tubo y pendiente son:

La variancia de la capacidad de la alcantarilla se calcula como:

La desviación estándar de la capacidad del flujo es:

La media del gasto es:

La probabilidad de falla es:
pF = 1 - 0.9699 = 0.0301
Método de Rosenblueth
En cuanto al problema de la alcantarilla analizada, supóngase que los tres parámetros de la ecuación de Manning son variables aleatorias.
Considerando la fórmula de Manning en la que:
W = Q = 0.463 n—1 D 2'67S0.5 - 35
Con tres variables aleatorias hay un total de 23 = 8 posibles puntos a ser considerados con el método de Rosenblueth. Debido a que hay tres variables simétricas, el coeficiente de asimetría es igual a cero, por lo que de acuerdo con las ecuaciones (24) a (27):

Y los valores correspondientes del coeficiente de rugosidad, diámetro de la alcantarilla y pendiente son:
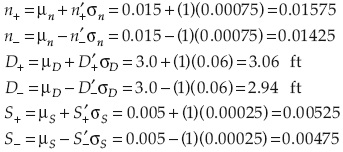
Sustituyendo los valores de n'-, n'+, D'-, D'+, S'-y S'+ en la ecuación de Manning, se obtiene, por ejemplo:
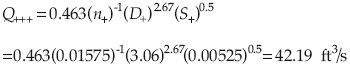
Similarmente, los valores de la capacidad de la alcantarilla para los otros siete puntos están dados en el cuadro 5.
Debido a que el coeficiente de rugosidad y el diámetro de la alcantarilla son simétricos, las variables correlacionadas de las variables aleatorias pueden determinarse con las ecuaciones (32) y (33).

Los valores de probabilidad en masa tabulados se muestran en la última columna. El momento de orden mésimo alrededor del origen para determinar la capacidad del flujo puede determinarse con la ecuación (31), como se muestra en el cuadro 6.
Del cuadro 6, μw = E(Q) = 41.22 ft3/s y E(Q2) = 1 715.994 (ft3/s)2.
Entonces la variancia de la capacidad del flujo de la alcantarilla puede estimarse como:
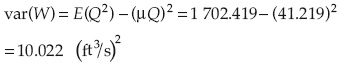
Por lo tanto, la desviación estándar de la capacidad de flujo de la alcantarilla es 
Comparando con los resultados anteriores, se observa que el método de estimación probabilística de Rosenblueth arroja valores más altos de media y variancia que los obtenidos con el método de estimación de primer orden de la variancia (FOVE).
Para estimar la confiabilidad:

La probabilidad de falla es:
pF = 1- 0.97381 = 0.02619
Método de aproximación probabilística de Harr. Método del punto de estimación
De acuerdo con la ecuación (38), las coordenadas de los 2 x 3 = i puntos de intersección que corresponden a los tres eigen vectores y la hiperesfera con radio √3 pueden determinarse como:

Dónde Vi es un vector con valor  ya que las variables no están correlacionadas.
ya que las variables no están correlacionadas.
Las coordenadas resultantes de los seis puntos de intersección de estas ecuaciones se enlistan en la columna 2 del cuadro 7. Sustituyendo valores de x (columna 2) en la fórmula de Manning se calculan los correspondientes al gasto (columna 3); los valores de Q2 se presentan en la columna 4, calculando el segundo momento respecto al origen.
Se obtienen las columnas 3 y 4, y los valores promedio de Q y Q2 a lo largo de cada eigen vector son calculados y listados en las columnas 5 y 6, respectivamente.
De acuerdo con la ecuación (40), con m = 1 se puede calcular el valor medio de la capacidad de la alcantarilla como:
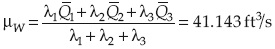
El segundo momento respecto al origen se calcula como:
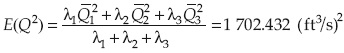
La variancia del flujo en la alcantarilla es:

La probabilidad de falla es:
pf = 1 - ps = 0.02438
Método del valor medio del primer orden del segundo momento (MFOSM)
Los procedimientos para estimar el método de primer orden del segundo momento estadístico se muestran con detalle en la literatura especializada que describe el método FOVE para el análisis de incertidumbres.
Una vez que se han estimado la media y la desviación estándar de W(X), la confiabilidad se expresa como:
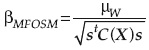
Con el método FOVE se estimó que:
• La media del gasto y la desviación estándar son:

• La probabilidad de falla es:
pF = 1 - 0.9699 = 0.0301
Método avanzado del primer orden del segundo momento (AFOSM) según Hasofer-Lind
Tomando en cuenta el algoritmo de Hasofer-Lind con el método AFOSM, la ecuación de comportamiento se puede expresar como:
W(n, D, S) = QT-QC = 35-0.463n-1D2.67S0.5
El algoritmo que se sigue es:
1. Elegir una solución de prueba X(r) con los valores medios iniciales:
X= (μn, μD, μS)t = (0.015, 3.00, 0.005)t
2. Calcular W(X(r)) y el correspondiente vector s(r):
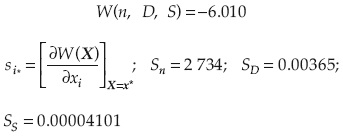
3. Revisar el punto de solución de acuerdo con la ecuación de comportamiento:
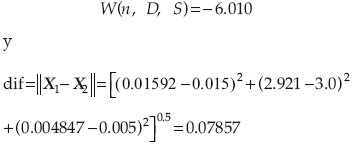
4. Verificar si X(r) y X(r+1) son lo suficientemente cercanos; en caso afirmativo, calcular βAFOSM con la ecuación:
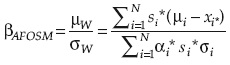
Y el índice de confiabilidad Ps = φ(βAFOSM).
Si X(r) ≠ X(r+1) entonces repetir 2; en caso contrario:
5. Calcular el índice de confiabilidad con respecto a los cambios de las variables estocásticas.
El cálculo se muestra en el cuadro 8. En este caso, la media y desviación estándar del gasto son:
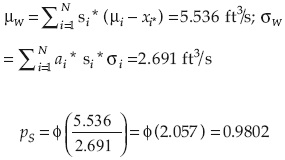
La probabilidad de falla es:
pF = 1-0.9802 = 0.01983
La sensibilidad del método se muestra en el cuadro 9.
En el cuadro 9, las cantidades  y
y  muestran las sensibilidad del índice de confiabilidad por el cambio de una vez de la desviación estándar, mientras que muestra que
muestran las sensibilidad del índice de confiabilidad por el cambio de una vez de la desviación estándar, mientras que muestra que  corresponden al cambio unitario de las variables aleatorias en el espacio original.
corresponden al cambio unitario de las variables aleatorias en el espacio original.
La sensibilidad de β y pS asociadas con el coeficiente de Manning son negativas; mientras que las asociadas con el diámetro y la pendiente son positivas; esto indica que un incremento en el coeficiente de Manning resultaría en un decremento de β y pS, mientras que un incremento en la pendiente y en el tamaño del tubo incrementarán β y pS.
Hidráulicamente esto se explica, ya que un incremento en la rugosidad provoca necesariamente un decremento en el gasto, y un incremento en el diámetro o la pendiente significa una mayor capacidad en la conducción.
Método avanzado del primer orden del segundo momento (AFOSM) según Tang
La función de comportamiento del problema si:
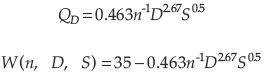
Con los parámetros estadísticos:

Si se adoptan como constantes:
C11 = 0.463; C21 =-1.0; C3 = 2.67; C4 = 0.5
Las derivadas parciales del gasto son:

Y la función de comportamiento con el margen de seguridad es:
W(n, D, S) = 35 - 0.463n-1D2.67S0.5
La primera iteración se hace considerando los valores medios de la variable:
W(n, D, S) = 35 -41.00988 = -6.00988 >>0
Las parciales son:

El cálculo se resume en el cuadro 10. La ecuación de falla es:

Que se resuelve para β = 3.39211.
Para ejemplo en particular, la solución con el algoritmo de Tang es:

El coeficiente de confiabilidad es β = 3.39211:
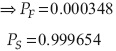
Discusión de resultados
El resumen de los métodos de estimación de riegos se muestra en el cuadro 11.
Se pueden señalar las siguientes observaciones:
1. Se puede adoptar como método exacto el obtenido con el de integración directa; sin embargo, hay que considerar que se supuso que los resultados obtenidos obedecen al hecho de adoptar que las variables estudiadas tienen una función de distribución lognormal; en casos analizados con incertidumbres más grandes que las estudiadas, este método puede no tener aplicación.
2. El método de Monte Carlo arroja resultados parecidos al de integración directa, con una diferencia ΔPF = 0.07852 (7.852%); puede usarse como referencia para la estimación del riesgo, aunque en los casos analizados que poseen variables con distribuciones de probabilidad diferentes a la normal, el análisis presente una mayor complejidad en su evaluación.
3. Si el resultado exacto se adopta como el obtenido con el método de integración directa, el que más se parece es el de Hasofer, con una variación del índice de confiabilidad Δβ = 0.3113% y del 0.1% en cuanto a la probabilidad de falla PF.
4. El siguiente resultado en aproximación es el que se obtiene con el método de Harr con Δβ = 3.76% y del 13.79% en cuanto a la probabilidad de falla PF.
5. Los resultados obtenidos con el método de la transformada de Mellin y los obtenidos con el método de Rosenblueth son muy similares (difieren entre sí un Δβ = 0.581% en cuanto al índice de confiabilidad y un 2.329% en cuanto a la probabilidad de falla).
6. El método FOVE y el de primer orden (que se basan en las misma hipótesis) es el más lejano, con una variación del Δβ = 9.086%.
7. Los resultado obtenidos con el método de Tang, por ser un análisis hecho en una condición límite del espacio multidimensional, parecen exagerados, ya que la variación es del Δβ = 65.42% superior al de integración directa; sin embargo, por ser precisamente obtenidos en la superficie de falla parecieran ser más realistas en el momento que se consideran todas las variables que intervienen en el análisis.
Conclusiones y recomendaciones
El riesgo, la confiabilidad y el análisis de incertidumbres pueden aplicarse en proyectos de ingeniería hidráulica, al estimar la probabilidad de falla en cuanto a capacidad hidráulica de alcantarillas y conducciones, desbordamiento, filtración, sismos, etcétera, en presas y diversos problemas más.
Cada método tiene sus propias hipótesis y limitaciones, ventajas y desventajas. La mayoría de los métodos puede aplicarse y es posible obtener estimaciones confiables cuando los métodos se aproximan a comportamientos lineales, pero cuando se tiene una no linealidad de las variables o bien cuando las incertidumbres se incrementan significativamente, la precisión de algunos métodos se deteriora rápidamente. Tal es el caso del método del primer orden del segundo momento estadístico.
Para métodos con muestras de gran tamaño en sus variables, el método de Monte Carlo es el de mayor aplicación, pero su confiabilidad converge cuando se tiene un gran número de simulaciones y no se conoce estrictamente el resultado final de la probabilidad de falla; otra limitante importante es que el número de variables puede hacer que el problema no tenga una solución práctica.
Métodos en los que se emplea el punto de estimación (Rosenblueth y Harr), por ejemplo, pueden ser muy atractivos desde el punto de vista computacional, en la medida en la que el número de variables se incrementa y pueden parecer muy buenos en su empleo, ya que ofrecen resultados parecidos a los obtenidos con el método de Monte Carlo y el de integración directa; sin embargo, en caso de que las incertidumbres sean importantes, pueden existir diferencias significativas con tales métodos.
El método del primer orden del segundo momento estadístico es aplicable sólo en casos muy sencillos, en los que la función de comportamiento está claramente definida y existe una linealidad en las variables; sin embargo, en problemas complejos pierde precisión rápidamente. El método del primer orden del segundo momento estadístico es muy aplicable y puede tomar en cuenta incertidumbres en el caso de que el analista decida hacer correlaciones de las variables que intervienen en el problema y que la mayor parte de las veces se asocia con incertidumbres; ésta parece ser una gran ventaja sobre los demás métodos, ya que es posible involucrar variables que en muchas ocasiones se ignoran o desprecian por no poder analizarlas.
El método de Hasofer en problemas simples parece ser bastante apropiado; sin embargo, el método de Tang resulta muy atractivo al analizar el estado límite de falla del problema estudiado.
Notación
Los siguientes símbolos se utilizan en este documento:
C(X) = matriz de covariancia de las variables aleatorias X.
D = diámetro de la conducción.
D = matriz diagonal que involucra las variancias de las variables aleatorias.
DPA = distribución de probabilidad acumulada.
E(W) = esperanza del modelo W.
FM(0) = función de distribución de probabilidad del margen de seguridad.
FS = capacidad de resistencia del sistema.
fX(X) = función de distribución de probabilidad de la variable aleatoria X.
MS = capacidad de resistencia del sistema.MX(S) = transformada de Mellin de la función fX(X).
N = número de variables aleatorias X.
n = coeficiente de rugosidad de Manning.
PF = probabilidad de falla.
Ps = probabilidad de seguridad (no falla) en el que la resistencia del sistema excede la carga.
Q = gasto o capacidad de descarga.
R = riesgo.
S = pendiente de plantilla.
s* = vector de sensibilidad de los coeficientes de la función de comportamiento W(X) evaluado en el punto de expansión X*.
Tr = periodo de retorno.
W(X) = función de comportamiento o desarrollo de las variables aleatorias X.
X = capacidad de resistencia del sistema.
x' = variable estandarizada.
Y = capacidad de demanda o carga del sistema.
Z = variable aleatoria continua.
αi* = derivada direccional para la variable iésima en el punto x*.
β = coeficiente o índice de confiabilidad.
ε = representa los términos de orden superior de la serie de Taylor desarrollada para la función g(x).
μ = media de las variables.
ρ = coeficiente de correlación entre variables aleatorias.
σ = desviación estándar.
σ2 = varianza.
V = matriz de eigen vectores.
Î = matriz diagonal compuesta de eigen valores.
Referencias
ANG, A., ANG, G.L. and TANG, W.H. Multidimensional Kernel method in importance sampling. ICASP no. 6, México, D.F., 1991. [ Links ]
ANG, A. and CORNELL, C.A. Reliability of structure safety and design. Journal of the Structure Division, ASCE. Vol. 100, no 9, September, 1974, pp. 1755-1769. [ Links ]
BORGMAN, L.E. Risk criteria. Journal of Waterways an Harbors Div. American Society of Civil Engineers. Vol. 89, no. WW3, 1963, pp. 1-35. [ Links ]
CHOW, V.T. Frequency-Analysis of hydrologie data with special aplication to rainfall intensities. Bulletin 414. Urbana, USA: University of Illinois Engineering Experimental Station, 1953. [ Links ]
CORNELL, C.A. Structural safety specifications based on second moment analysys. Final report of the IABSE. Symposium on Concepts of Safety Structures and Methods of Design, London, 1969. [ Links ]
DUCKSTEIN, L. and BOGARDI-SZIDAROVSKY, I. Reliability of underground flood control system. Journal of the Hydraulics Division. ASCE. Vol. 107, July, 1981, pp. 817-827. [ Links ]
HAAN, C.T. Adequacy of hydrologic records for parameter estimation. Journal of the Hydraulics Division. Vol. 98, ASCE, August, 1972, pp. 1387-1393. [ Links ]
HARR, M.E. Probabilistic Estimates for Multivariate Analyses. Applied Mathematical Modelling. Vol. 13, 1989, pp. 313-318. [ Links ]
HOSHIYA, M., KUTSANA, Y. and FUJITA, M. Adaptive estimation of structural reltability by importance sampling, ICASP no. 6, México, D.F., 1991. [ Links ]
KARMESHU, F. and LARA-ROSANO, F. Modelling Data Uncertainty in Growth Forecasts. Applied Mathematical Modelling. Vol. 1, 1987, pp. 62-68. [ Links ]
IBRAHIM, Y. and RAHMAN, S. Reliability analysis of uncertain using systems using importance sampling. ICASP no. 6, México, D.F., 1991. [ Links ]
LEIRA, J.B. Importance sampling distributions for Gaussian vector process. México, D.F.: ICASP, 1991. [ Links ]
MCKAY, M.D., BECKMAN, R.J. and CONOVER, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics, Vol. 21, 1979, pp. 239-245. [ Links ]
MARENGO, M.H. Análisis de riesgo de falla en presas, estadísticas y parámetros de referencia. Ingeniería hidráulica en México. Vol. XI, núm. 2, mayo-agosto de 1996, pp. 65-77. [ Links ]
MARENGO, M.H. Case Study: Dam safety during construction, lessons of the overtopping diversion works at Aguamilpa dam. Journal of Hydraulic Engineering. ASCE. Vol. 132, no. 11, November, 2006, pp. 1121-1127. [ Links ]
MATALAS, N.C., SLACK, J.C. and WALLIS, R. Regional skew in search of a parent. Water Resources Research. Vol. ll, no. 6, 1975, pp. 815-826. [ Links ]
MAYS, L.W. and TUNG, Y.K. Hydrosystems Engineering and Management. New York: McGraw-Hill, 1992. [ Links ]
PARK, C.S. The Mellin Transform in Probabilistic Cash Flow Modeling. The Enginnering Economist. Vol. 32, no. 2, 1987, pp. 115-134. [ Links ]
RACKWITZ, R. and FIESSLER, B. Non-normal distributions in -structural reliability. SFB 96, Technical University of Munich, Ber Zur Sicherheitstheorie der Bauwerke no. 29, 1978, pp. 1-22. [ Links ]
ROSENBLUETH, E. Point estimates for probability moments. Procedings. National Academy of Science. Vol. 72, no. 10, 1975, pp. 3812-3814. [ Links ]
ROSENBLUETH, E. Two-point estimates in probabilities. Applied Mathematical Modelling. Vol. 5, 1981, pp. 329-335. [ Links ]
SPRINGER, M.D. The Algebra of Random Variables. New York: John Wiley and Sons, 1979. [ Links ]
TANG, W.H. Probability concepts in engineering planning and design. Vol. I, Basic Principles. Vol. 11, Decision, Risk, and Reliability. New York: Wiley and Sons, 1984. [ Links ]
TANG, W.H. bayesian frequency analysis. Journal of the Hydraulics Division. ASCE. Vol. 106, July, 1980., pp. 1203-1218. [ Links ]
U.S. ARMY CORPS OF ENGINEERING. Recomended guidelines for safety inspection of dams. ER 1110-2-106. Vol. 1. Appendix D. Washington, D.C.: National Program Inspection of Dams, 1979. [ Links ]
VRIJLING, J.K. Development of probabilistic design in flood defenses in the Netherlansds. Reliability and Uncertainty Analysis in Hidraulic Design. Yen, B.C. and Tung, Y.K. (editors). New York: ASCE, 1993, pp. 133-178. [ Links ]
WEN, Y.K. Statistical combination of extreme loads. Journal of the Structural Division. ASCE. Vol. 103, no. 5, May, 1977, pp. 1079-1093. [ Links ]
WOOD, E.F. An analysis of flood levee reliability. Water Resources Research. Vol. 13, no. 3, 1977, pp. 665-671. [ Links ]
Nota
Publicado por invitación.















