Nota técnica

 

Descripción de un modelo físicamente basado para el análisis de frecuencia de crecientes

 

Description of a physically based model for flood frequency analysis

 

Daniel Francisco Campos-Aranda

 

Profesor jubilado de la Universidad Autónoma de San Luis Potosí, México.

 

Dirección institucional del autor

Dr. Daniel Francisco Campos-Aranda

Profesor jubilado de la Universidad Autónoma de San Luis Potosí
Genaro Codina 240, Colonia Jardines del Estadio
78280 San Luis Potosí, San Luis Potosí, México
campos_aranda@hotmail.com

 

Recibido: 13/05/2009
Aprobado: 09/08/2009

 

Resumen

Inicialmente se expone una clasificación para los modelos probabilísticos utilizados en el análisis de frecuencia de crecientes local. Enseguida se presenta un resumen de los aspectos teóricos y estadísticos asociados con el llamado modelo de analogía de difusión lineal, el cual constituye una distribución probabilística físicamente basada. Posteriormente se describe su aplicación numérica en cinco registros de gastos máximos anuales de la cuenca baja del río Pánuco. Por último, se analizan los resultados y se formulan las conclusiones, las cuales destacan la conveniencia de este modelo en estaciones hidrométricas de gran área drenada en ríos de planicie.

Palabras clave: modelo lineal, modelo de difusión, distribuciones de probabilidad, método de momentos, error estándar de ajuste, río Pánuco.

 

Abstract

First, a classification is presented for the probabilistic models used in local flood frequency analysis. Then, a summary is given of the theoretical and statistical aspects associated with the so-called linear diffusion analogy model, which is a physically based probabilistic distribution. Next, its numerical application in described in five records of annual maximum flows of the lower Pánuco River watershed. Finally, results are analyzed and conclusions drawn, which point to the suitability of this model in hydrometric stations with a large drainage area in lowland rivers.

Keywords: linear model, diffusion model, probability distributions, method of moments, standard error of fit, Pánuco River.

 

Introducción

El análisis de frecuencia de crecientes (AFC) ha sido un tema de gran interés práctico y de mucha investigación dentro de la hidrología y el desarrollo de los recursos hidráulicos, principalmente debido a que permite el dimensionamiento de la infraestructura hidráulica, desde los vertedores de los embalses para brindar seguridad en éstos, hasta las obras de cruce (alcantarillas y puentes) y de protección (diques, encauzamientos y rectificaciones). Como resultado de tales tendencias, en el AFC se utilizan diversos enfoques y variados modelos matemáticos (Campos, 1999), los cuales, de manera general, se clasifican en locales o del sitio, y regionales. Por su parte, los modelos probabilísticos que se utilizan en el AFC local se pueden clasificar en los siguientes tres tipos (Strupczewski et al., 2001): (1) empíricos, (2) fenomenológicos y (3) físicamente basados.

El enfoque empírico es actualmente el más común. Consiste en utilizar modelos o distribuciones de probabilidad que han sido propuestas para realizar el AFC, mismas que han demostrado su conveniencia o bondad de ajuste. Stedinger et al. (1993), y Rao y Hamed (2000) exponen con detalle esta aproximación. En el enfoque fenomenológico se utilizan axiomas probabilísticos, los cuales conducen a la formulación de un modelo matemático de una o más características de las crecientes. Son ejemplos de esta aproximación la modelación estocástica de crecientes y la aplicación de la teoría de la entropía. Este tratamiento no llegó a ser popular debido a su sofisticación matemática. Por último, en el enfoque de los modelos físicamente basados se emplean principios dinámicos de la generación de las crecientes para obtener un modelo probabilístico. En este contexto, Strupczewski et al. (2001) utilizaron los modelos de tránsito de gasto en canales, en los cuales no se hace una consideración explícita a los procesos hidrológicos que ocurren en los suelos de la cuenca para desarrollar una función de densidad de probabilidad con dos parámetros de ajuste.

El objetivo de este trabajo consiste en exponer un resumen de la teoría del modelo de analogía de difusión lineal (MADIL) desde su concepción hasta las ecuaciones de su aplicación como distribución probabilística, incluyendo su aplicación y contraste en cinco estaciones hidrométricas de la cuenca del bajo río Pánuco o Región Hidrológica Número 26, de México.

 

Desarrollo

Resumen de teoría

Aceptando que el volumen unitario de la función impulso δ de Dirac consiste de un número infinito de partículas o gotas, entonces la integral de la respuesta impulso, es decir:

determina la probabilidad de que una partícula individual pase por la salida s durante el tiempo (0,T), donde h(s,t) es la función a la respuesta impulso en el tiempo t en la posición s. Además de esta interpretación probabilística, la función citada debe cumplir con los requerimientos de los modelos probabilísticos empleados en el AFC, como son: límite inferior no negativo, sesgo positivo y ser unimodal.

Por otra parte, la predicción de las características de una creciente (gasto pico y volumen) en una sección aguas abajo de un río, con base en las condiciones conocidas del flujo o hidrograma en una sección de aguas arriba, es el problema fundamental del tránsito de crecientes. Usando una linealización de las ecuaciones de Saint Venant (Dooge y Harley, 1967; Napiórkowski, 1992) se obtiene un modelo lineal físicamente basado con cuatro parámetros dependientes de las características hidráulicas del tramo de cauce, cuya solución aún es compleja. Se desarrollaron dos versiones simplificadas: el modelo de analogía de difusión lineal o modelo convectivo-difusivo lineal, y el modelo de flujo rápido lineal, los cuales corresponden a condiciones límites del flujo establecidas con el número de Froude de cero y de uno, respectivamente. La respuesta impulso del primer modelo está dada por (Strupczewski et al., 2001):

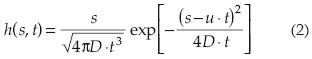
donde s es la longitud de tramo de canal, t es el tiempo, u es la velocidad convectiva y D es la difusividad hidráulica. Tanto u como D son funciones de las características del canal y del flujo en la condición de referencia de flujo estable. Designando 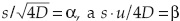y a t como x, se obtiene la función de densidad de probabilidad con dos parámetros de ajuste del modelo de analogía de difusión lineal (MADIL):

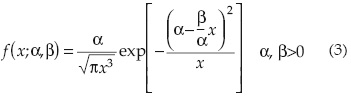
α es el parámetro de escala con dimensión de raíz cuadrada de las unidades de la variable aleatoria x y β es el parámetro de forma adimensional. Este modelo probabilístico ha sido estudiado desde finales de la década de los años cincuenta por diversos matemáticos y estadísticos, siendo denominado distribución Gaussiana inversa.

Principales propiedades estadísticas

Los coeficientes de variación, asimetría y kurtosis son (Strupczewski et al., 2001):

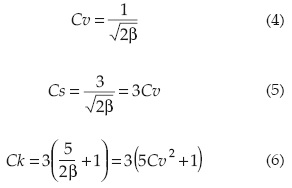
la moda es:

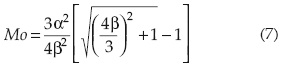
Cuando Cv → 0, la distribución tiende a ser simétrica, como los modelos Log-Normal y Gamma. La ecuación (5) establece que en el MADIL, el cociente Cs/Cv es igual a tres; en cambio, en la distribución Gamma es de dos, y en la Log-Normal existe esta relación: Cs = 3Cv + Cv². Estas tres distribuciones y la Weibull han sido contrastadas por Mitosek et al. (2006) en varios ríos de Polonia, con registros de gastos máximos anuales del orden de setenta años, encontrado como mejores opciones el MADIL y la distribución Log-Normal. Para todas las distribuciones citadas se han desarrollado versiones matemáticas que incluyen dos parámetros de forma, con la idea de buscar un mejor ajuste en su porción o cola derecha (Strupczewski et al., 2008).

Estimación de parámetros y de su dispersión

Los métodos de momentos (MMO) y de máxima verosimilitud (MMV) conducen respectivamente a las expresiones siguientes para los parámetros de escala y forma (Strupczewski et al., 2001):

en donde 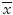es la media aritmética y H, la media de los recíprocos; es decir:

siendo x_i los gastos máximos anuales (m³/s) de la serie o muestra que se procesa, cuyo número de datos es n.

Las ecuaciones (10) y (11) del MMV están basadas en las medias aritmética y de recíprocos, por lo tanto sus estimaciones no son sensibles a los grandes valores de x en la muestra (outliers). Lo anterior significa que este método conduce a un buen ajuste en la porción izquierda de la distribución; en cambio, con el MMO se logra un mejor ajuste en parte extrema de los datos y por ello es el preferido (Strupczewski et al., 2001).

Las dispersiones de los parámetros de ajuste D(α) y D(β), expresadas como error estándar, son en el MMO las siguientes:

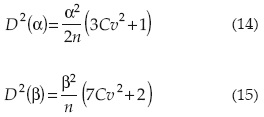
Se observa que en ambos casos tales dispersiones dependen directamente de la variabilidad de los datos e inversamente de la longitud de la muestra.

Estimación de predicciones

El valor de x asociado con una determinada probabilidad de excedencia p(x_p) o predicción se obtiene integrando la ecuación (3), lo cual conduce a:

en la cual φ_p es el límite superior de la siguiente integral:

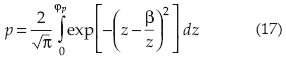
La solución de tal integral se obtuvo mediante la cuadratura de Gauss, utilizando el polinomio de Legendre aplicado a cualquier intervalo de integración y mediante una fórmula de diez puntos (Nakamura, 1992; Campos, 2003). Algunos valores de φ_p para las magnitudes de β y de p que ocurren y se usan en la práctica se exponen en el cuadro 1.

Strupczewski et al. (2001) presentan las ecuaciones para estimar la dispersión en las predicciones D(x_p), así como sus valores relativos 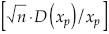en forma tabular para las magnitudes de β y de p que ocurren y se usan en la práctica. Tales valores relativos se reproducen en el cuadro 2.

Aplicaciones numéricas

Strupczewski et al. (2001) encontraron que el ajuste del MADIL fue notablemente mejor en los registros de las estaciones hidrométricas con grandes áreas de cuenca (> 10 000 km²), es decir, en ríos de planicie, donde el modelo convectivo-difusivo lineal es una buena aproximación para modelar el tránsito de crecientes. Por ello, las aplicaciones numéricas del MADIL que serán expuestas con propósitos descriptivos se realizaron en las estaciones de aforos finales de la Región Hidrológica Número 26 (Pánuco), las cuales se ubican en la planicie costera del golfo de México.

En el cuadro 3 se exponen las características generales de las cinco estaciones hidrométricas procesadas y las propiedades estadísticas de sus registros de gasto máximo anual. Las series de las estaciones Tamesí y Pánuco han sido expuestas por Campos (2007) y la de Magiscatzin II se presentó en Campos (2006). Las muestras de las estaciones El Pujal y Tempoal proceden del sistema BANDAS (IMTA, 2002). Todos los registros citados se tienen en el cuadro 4.

Por otra parte, en el cuadro 5 se exponen los resultados de las ecuaciones (8), (9), (14) y (15); es decir, del cálculo de los parámetros de ajuste y sus dispersiones.

Contraste y error estándar de ajuste

A los cinco registros hidrométricos procesados (cuadro 4) se les aplicaron las distribuciones Log-Pearson tipo III (LP3), a través del método de momentos en sus dominios logarítmico y real (Bobée y Ashkar, 1991), así como la General de Valores Extremos (GVE), por medio de los métodos de momentos, sextiles, máxima verosimilitud y momentos L (Campos, 2001), seleccionando el ajuste que condujo al menor error estándar de ajuste (EEA), definido como (Kite, 1977):

en donde n es el número de datos del registro; x_i, los gastos máximos anuales observados, ordenados de menor a mayor; , los gastos máximos estimados con el modelo probabilístico que se prueba, para una probabilidad de no excedencia, definida con la fórmula Weibull

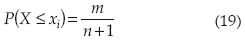
en la cual X es la variable aleatoria, cuyo límite es x_i; m es el número de orden del dato (x_i), con uno para el menor y n para el mayor. Finalmente, np es el número de parámetros de ajuste: np=2 para el MADIL y np=3 para los modelos LP3 y GVE.

Como el MADIL (ecuaciones (16) y (17) no tiene solución inversa; es decir, que no se puede estimar directamente el valor de x asociado con una determinada probabilidad de no excedencia F(x), entonces, para el cálculo del EEA, se utilizó el procedimiento de bisección sugerido por Campos (1989); para ello se proponen valores iniciales inferior (xi=0.0001·x_i) y superior (xs=10x_i); se obtiene su media aritmética 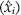; con tal magnitud se obtiene φ_p (ecuación (16)) y después F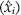=p con la ecuación (17); se compara este último valor con el de la ecuación (19), relativo al x_i y si su diferencia absoluta no es menor que 0.00001, que es la tolerancia aceptada, se sigue el método de bisección.

Análisis de los resultados

En el cuadro 6 se han concentrado las predicciones obtenidas con los tres modelos probabilísticos aplicados, en las cuales se observa gran similitud en los periodos de retorno bajos (<50 años); en cambio, en los intervalos de recurrencia extrema (>500 años) se tienen diferencias significativas en Tempoal y Magiscatzin II, que son las estaciones hidrométricas con los cocientes Cs/Cv más alejados de tres.

Al respecto, Strupczewski et al. (2001) encontraron en 39 ríos polacos un cociente Cs/Cv medio de 2.52; esto es, un valor más cercano al MADIL que al de las distribuciones Gamma y Log-Normal; por ello, tal modelo fue el más conveniente en 27 de tales registros.

En el resto de las estaciones, las predicciones del MADIL coinciden con las de las distribuciones LP3 y GVE, que son modelos más flexibles al tener tres parámetros de ajuste, mismos que han demostrado su bondad de ajuste y por ello su aplicación ha sido establecida como precepto en Estados Unidos e Inglaterra, respectivamente.

Respecto al error estándar de ajuste (EEA), en general son del mismo orden de magnitud en los tres modelos probabilísticos aplicados. El MADIL en la estación El Pujal conduce al mayor EEA, sin embargo sus predicciones son coincidentes con las de la distribución LP3.

En la figura 1 se muestra el ajuste del MADIL a los datos de la estación hidrométrica Pánuco; además, se indica la dispersión de las predicciones, estimadas para β=3 con base en los valores del cuadro 2.

 

Conclusiones

En estaciones hidrométricas con gran área drenada ubicadas en ríos de planicie, en los cuales la aproximación lineal para el tránsito de crecientes es válida y donde además el cociente entre los coeficientes de asimetría y de variación de su registro de gastos máximos anuales sea cercano a tres, es muy probable que el MADIL sea la distribución de probabilidades más conveniente.

Este modelo probabilístico físicamente basado tiene la ventaja de ser fácilmente aplicable y cuya evaluación de sus parámetros de ajuste utiliza dos propiedades estadísticas básicas: la media aritmética y la desviación estándar a través del Cv, esto implica una estimación más confiable.

 

Referencias

BENSON, M.A. Plotting positions and economics of engineering planning. Journal of Hydraulics Division. Vol. 88, HY6, 1962, pp. 57-71.         [ Links ]

BOBÉE, B. and ASHKAR, F. The Gamma family and derived distributions applied in hydrology. Chapter 7: Log-Pearson type 3 distribution. Littleton, USA: Water Resources Publications, 1991, pp. 76-120.         [ Links ]

CAMPOS, D.F. Estimación de los parámetros óptimos de la distribución Gumbel Mixta por medio del algoritmo de Rosenbrock. Ingeniería hidráulica en México. Vol. IV, núm. 1, 1989, pp. 9-18.         [ Links ]

CAMPOS, D.F. Hacia el enfoque global en el análisis de frecuencia de crecientes. Ingeniería hidráulica en México. Vol. XIV, núm. 1, 1999, pp. 23-42.         [ Links ]

CAMPOS, D.F. Contraste de cinco métodos de ajuste de la distribución GVE en 31 registros históricos de eventos máximos anuales. Ingeniería hidráulica en México. Vol. XVI, núm. 2, 2001, pp. 77-92.         [ Links ]

CAMPOS, D.F. Introducción a los métodos numéricos: software en Basic y aplicaciones en hidrología superficial. Capítulo 7: Integración Numérica. San Luis Potosí, México: Librería Universitaria Potosina, 2003, pp. 137-153.         [ Links ]

CAMPOS, D.F. Contraste de métodos regionales de estimación de crecientes en la cuenca del río Guayalejo, en Tamaulipas. Tláloc. Núm. 37, 2006, pp. 14-24.         [ Links ]

CAMPOS, D.F. Contraste de métodos regionales para predicción de crecientes basado en la distribución GVE, en la cuenca baja del río Pánuco. Ingeniería hidráulica en México. Vol. XXII, núm. 2, 2007, pp. 91-105.         [ Links ]

DOOGE, J.C.I. and HARLEY, B.M. Linear routing in uniform open channels. Proceedings of the International Hydrology Symposium. Vol. 1, paper no. 8. Colorado State University, Fort Collins, USA, 1967, pp. 57-63.         [ Links ]

IMTA. Banco Nacional de Datos de Aguas Superficiales (BANDAS). 8 CD's. Jiutepec, México: Comisión Nacional del Agua-Secretaría de Medio Ambiente y Recursos Naturales-Instituto Mexicano de Tecnología del Agua, 2002.         [ Links ]

KITE, G.W. Frequency and Risk Analyses in Hydrology. Chapter 12: Comparison of frequency distributions. Fort Collins, USA: Water Resources Publications, 1977, pp. 156-168.         [ Links ]

MITOSEK, H.T., STRUPCZEWSKI, W.G. and SINGH, V.P. Three procedures for selection of annual flood peak distribution. Journal of Hydrology. Vol. 323, 2006, pp. 57–73.         [ Links ]

NAKAMURA, S. Métodos numéricos aplicados con software. Capítulo 7: Integración Numérica. México, D.F.: Prentice-Hall Hispanoamericana, S.A., 1992, pp. 109-154.         [ Links ]

NAPIÓRKOWSKI, J.J. Linear theory of open channel flow. Advances in Theoretical Hydrology. O'Kane, J.P. (editor). Amsterdam: Elsevier Science Publishers, 1992, pp. 3-15.         [ Links ]

RAO, A.R. and HAMED, K.H. Flood Frequency Analysis. Boca Raton, USA: CRS Press LLC, 2000, 350 pp.         [ Links ]

STEDINGER, J.R., VOGEL, R.M. and FOUFOULA-GEORGIOU, E. Frequency Analysis of Extreme Events. Handbook of Hydrology. Maidment, D.R. (editor). New York: McGraw-Hill, Inc., 1993, pp. 18.1-18.66.         [ Links ]

STRUPCZEWSKI, W.G., SINGH, V.P. and WEGLARCZYK, S. Impulse response of a linear diffusion analogy model as a flood frequency probability density function. Hydrological Sciences Journal. Vol. 46, no. 5, 2001, pp. 761-780.         [ Links ]

STRUPCZEWSKI, W.G., MARKIEWICZ, I., KOCHANEK, K. and SINGH, V.P. Short walk into two-shape-parameter flood frequency distributions. Hydrology and Hydraulics. Vijay P. Singh (editor). Highlands Ranch, USA: Water Resources Publications, 2008, pp. 669-716.         [ Links ]