text new page (beta)
English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
1. Introduction
Textual information can be classified into different themes, so it is important to identify features allowing organize this information on different topics. In this paper, we present a set of features focused on the task of automatic classification of multi-labelled documents.
In the automatic multi-labelled text classification, i.e. classification of documents given a set of themes (topics), can be assigned different labels or topics in a document according to its content. For example, a text with information about an oil well can be included in topics related to geographic, ecological, financial, political, etc. concepts.
The automatic classifiers are based on models of representation of a set or a corpus of documents, using a Vector Space Model (VSM). Using VSM means that we choose features of the documents and the values of these features and build a vector representation.
The most traditional features for text classification are words or n-grams that are present in the corpus with their values, tf-IDF weights (see below for more detailed description), are the most widely used model, however this representation has several problems 12:
High dimensionality of the vector space. The documents contain a lot of words or n-grams used as features, whose number determines a high dimensionality of the VSM.
A small number of features can be considered as irrelevant.
There are various ideas for dealing with these problems. For example, there are methods for reducing the dimensionality of Vector Space Models, for example, Latent Semantic Analysis or Latent Dirichlet Allocation (used in this paper). On the other hand, irrelevant features (for example, stop words) can be filtered using the idf measure or predefined lists of these words.
Recently, we proposed 30 to construct a vector space representation complementing it with other features, i.e., adding other features into the traditional VSMs. In a similar way, in 20 (the work presented at the same conference MICAI 2014, as our work 30, it is also proposed to complement the traditional VSM (they considered only lexical features: words and stems) with LDA for various number of topics (100, 200, 300, 400, 500) and with semantic spaces (HAL, COALS). By semantic spaces they mean distributional Vector Space Models, i.e., words from the context are used as features for each word. The stems were important for the authors because they experimented with highly inflective Czech language. Probably, using very traditional lemmatization would be sufficient in that situation. In our case, we have also exploited various n-gram models and not only lexical features as in [0]. We also complemented our models with LDA. We conducted our experiments for the traditional corpus for text classification: a subset of the Reuters' collection (in English). Interestingly, in this case n-gram models obtain better results. It is the unexpected conclusion, because it is well-known that for text classification task using words as features is usually the preferred alternative.
So, this paper proposes a method that allows the construction of a Vector Space Model for multi-label text classification using LDA complement. We used the Reuters-21578 corpus for the multi-label classification using the ideas mentioned above: 1 The Vector Space Model is generated using traditional tf-idf values for words and/or lexical n-grams as features; 2 It is complemented with its LDA representation. LDA allows recognizing the set of most probable topics that correspond to each document.
This method was tested with the multi-labeling algorithm called Rakel1 9 using the software called Meka 11. Rakel1 uses a Naive Bayes classifier as the base classifier. We always use lemmas of words and consider both possibilities for treatment of stop words (prepositions, articles, conjunctions, etc.): including or excluding stop words 12, 13, 14. As the baseline, we use the traditional tf-idf measure with words as features 14, 15, 16. Our best result is obtained using a combination of words and lexical bigrams with the LDA complement.
The structure of this paper is as follows. Section 2 describes the main concepts used in the paper. Section 3 presents related works. In Section 4, we describe our method. In Section 5, we discuss the obtained results and compare them with the baseline. Finally, we give conclusions and ideas for the future work in Section 6.
2. Text Classification Task
This section presents general concepts that are necessary for understanding of the further discussion.
2.1. Multi-Label Text Classification
Classification of documents is important within the area of information management, since it allows knowing different contexts or topics that correspond to documents. It is considered that words and word combinations (n-grams) from documents represent different semantic relations with other words and phrases within a particular context 1 and in this manner define the text's meaning. Detection of semantic relations (in a very broad sense) is included in the field of text classification 2, which refers to sorting a set of documents into a set of categories (topics, classes or labels). There are situations when some documents are assigned to more than one topic, which is known as multi-labeling 2, 6, 9, 10, 18. Text classification is based on techniques both from information retrieval and machine learning 2, 3, 4, 5.
2.2. TF, IDF and TF-IDF measures
The most common representation used in tasks of text classification 14, 15 is the Vector Space Model (VSM), in which each document is represented as a vector, whose components are the values of the VSM features. Each feature corresponds to a dimension in the vector space and the total size of the vector is given by the total number of features 8. The features in VSM are usually words (or their morphological invariants: lemmas or stems). Another widely exploited possibility is to use instead of words n-grams or syntactic n-grams 19.
VSM is also the representation used in multi-labeling algorithms. In case of texts, each document is transformed into a set of words/n-grams/syntactic n-grams which correspond to its vector representation. In the VSM, each element
Another value, which is measured with respect to the corpus, is called Inverse Document Frequency
where w refers to the word
where w refers to a word in the document d. Finally, the term
where N represents the total of documents in the corpus and
It is common practice (for example, Joachims 2, 13) to avoid using stop words (prepositions, articles, etc.), because they carry no lexical meaning and are present equally in all documents. But both possibilities: using them or excluding them should be analyzed experimentally.
2.3 Latent Dirichlet Allocation (LDA)
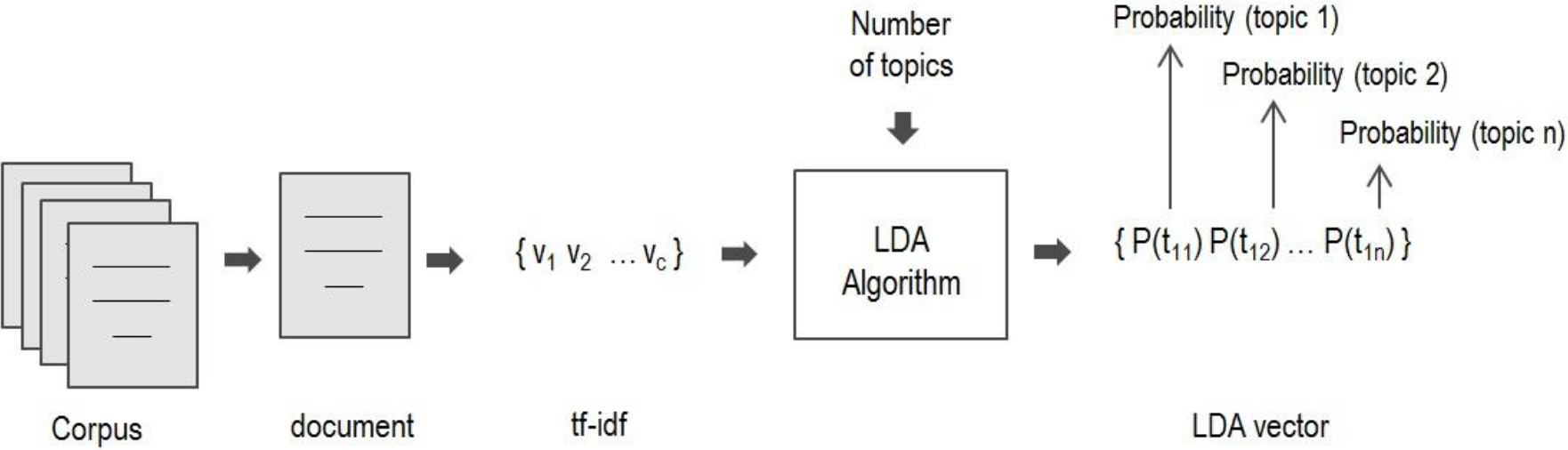
In natural language processing, Latent Dirichlet Allocation (LDA) refers to a probabilistic generative model for a corpus of documents, when the documents are represented as a combination of the probabilities of belonging to each topic in a Vector Space Model. Each topic is characterized by a probabilistic distribution based on a set of words (or n-grams, or syntactic n-grams) from the corpus. The number of topics is a parameter needed to choose the number of partitions to divide the corpus, when the LDA model is created.
For its computation, the LDA model takes as input the
The LDA algorithm contains the following steps.
For each document:
In an iterative process, for each word
Finally, the algorithm returns a new set of features for each topic and the probability of each document to belong to each topic.
3. Related Work
In the last years multi-label document classification has received special interest focusing primarily on the search for automatic document classification methods. The purpose is to identify groups of labels that correspond to the documents and replace the currently used human-assisted methods. These new methods are based on various feature sets and different classification algorithms.
Usually, these methods use the Vector Space Model and Term Frequency-Inverse Document Frequency
Among many works developed in the multi-label context we would like to mention some, which are closer related to our paper.
As we already mentioned, in 20 it is presented a new kind of characterization based on unsupervised stemmer, latent Dirichlet allocation (LDA) and semantic spaces (HAL and COALS) using the corpus of the Czech News Agency (CTK), where a document can belong to several topics such as politics, sports, culture, business, and others. This work uses as baseline (1)
Another work 10 proposes a new feature selection method called Labeled LDA, L-LDA. This paper refers to a probabilistic graphical model describing a process of generation of a set of labelled documents. This process is similar to the LDA process by regarding each document as a mixture of words belonging to different topics, except that the L-LDA process is supervised during the model creation. The L - LDA can be considered mainly as a model related to models of multinomial Naive Bayes classification.
In 26, it is shown that L-LDA is competitive. They use as the test corpus a Yahoo corpus with 4,000 documents and 20 labels. A set of binary classifiers based on support vector machines (SVM) is applied.
In 28, an algorithm called Rakel for multi-label classification is described (RAndom k-labELsets). It uses a method based on ensemble of classifiers LP (Label Powerset), in which each subset of tags is treated as a single label and from this assumption the classification is performed.
Note that the algorithms for multi-label classification can be divided into two different groups 9: (i) problem transformation, and (ii) adaptation algorithms. The first type refers to independent algorithms, where the problem of multi-label classification is divided into a particular bi-class classification and they are resolved as particular problems. Some algorithms in this group are label ranking 26, regression, etc. The second group uses adaptation of different classification algorithms to handle multi-label data. We can mention between these algorithms decision trees, support vector machines, neural networks, etc.
4. Proposed Method
The method developed in this work combines the Vector Space Model with its corresponding LDA model, which is used as a complement to create a new Vector Space Model. Our hypothesis is that it can improve the classification results. For classification, we use the multi-labeling algorithm Rakel1 implemented in Meka 11.
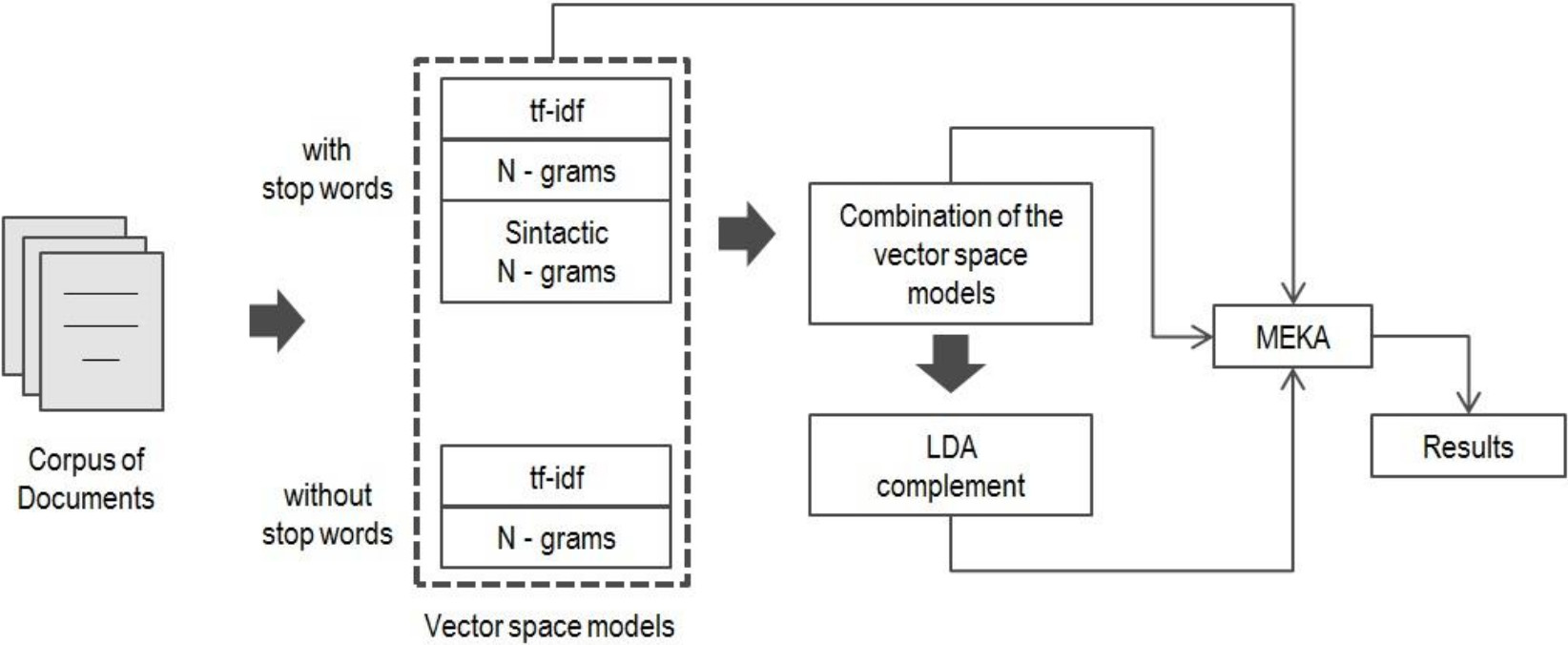
The proposed method comprises four stages, which are listed below and shown in Figure 2.
Construction of the traditional Vector Space Models (VSMs) using various feature sets,
Considering various combinations of these Vector Space Models,
Construction of the LDA complement and its inclusion into VSMs,
Multi-label classification (with MEKA).
As the first step, we create various traditional Vector Space Models using different feature sets: words (including stop words or ignoring them), n-grams and syntactic n-grams. We use lemmas of words and
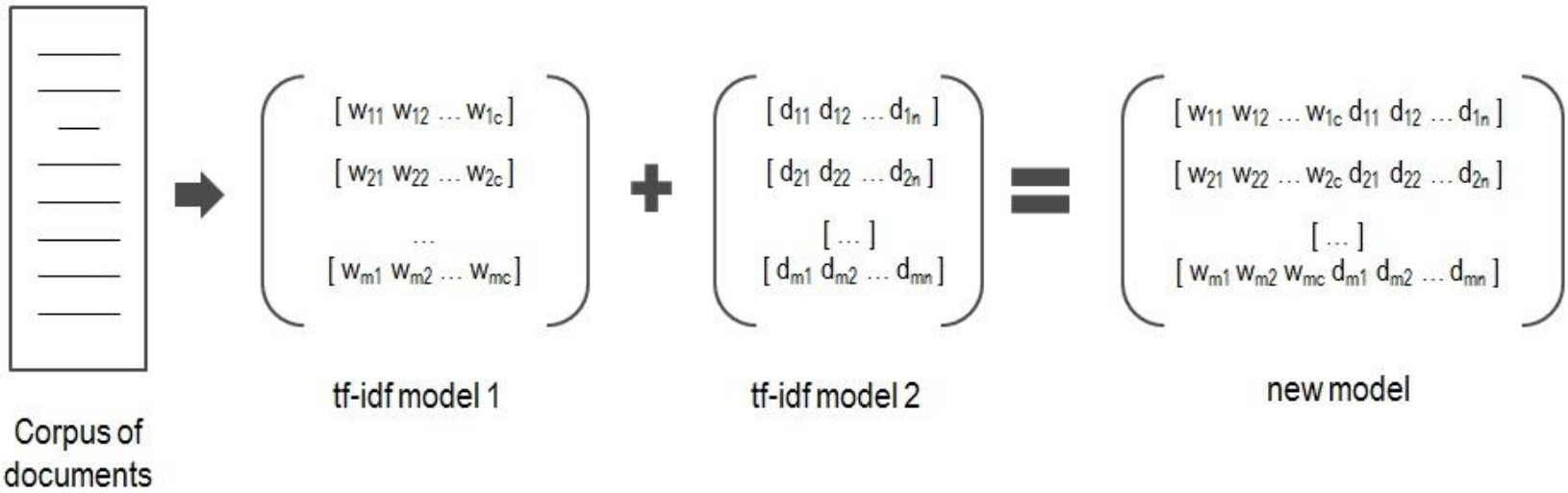
Further we consider combinations of each VSM with other VSMs, for example, we combine VSMs based on bi-grams with syntactic bi-grams. The combination of VSMs is presented in Figure 3.
For each Vector Space Model we apply the LDA algorithm using various numbers of topics to obtain it corresponding LDA-VSM. After this, a new Vector Space Model is created using a traditional or combined Vector Space Model and its respective LDA model. The combination consists in joining each vector of the first model with the respective vector of the LDA model.
We consider that the LDA models are a good complement because if two documents are similar, i.e., they have the same thematic labels, then their corresponding LDA vectors should be similar too. Our experiments show that using LDA complement allows obtaining better results. Note that the LDA complements have relatively small size, i.e., few dimensions are added. Still, they improve the classification.
For multi-label classification, we apply the Rakel1 algorithm 9 implemented in Meka for each VSM generated at the previous steps.
5. Experimental Setup
We developed the corresponding software in Python 2.7 using nltk and gensim libraries. We also use the Meka 1.3 and the software Core NLP of the Stanford University as lemmatizer.
We constructed the corpus that is part of the corpus Reuters-21578. Namely, we took the documents that are labelled with more than one class for 4 topics.
We use files in the corpus that were labeled with the following topics: interest, money-fx, wheat, grain, corn and dlr, considering 346 test files distributed in certain combinations as shown in Table 1. This is a subset of all topics in the corpus.
Table 1 Test corpus distribution
| Combinations of topics | Number of files |
|---|---|
| interest money-fx | 112 |
| wheat grain | 102 |
| corn grain | 67 |
| dlr money-fx | 65 |
5.1 Construction of the vector space models
For each file in the corpus, we identify words, applying typical tokenization process, creating a set of words, lemmatizing them and calculating their frequencies. Further, we consider them as features and also construct from them n-grams and syntactic n-grams. For obtaining syntactic n-grams, we apply the Stanford parser first 31. We also calculate
First of all, we construct two baseline VMSs: one of them considers all words in the corpus, denoted as unigrams-with_sw (where with_sw means "with stop words"), while the other one does not consider stop words (it is denoted as "unigrams").
We also constructed two VSMs using bigrams as features. One of them considers all words, while the other one does not consider stop word: called bigrams-with_sw and bigrams. Also, the VSM that considers syntactic bigrams (s-bigrams) was constructed. This VSM contains stop words.
Table 2 shows different number of features in each new Vector Space Model.
Table 2 Number of features in the new vector models.
| Vector Space Model | Features |
|---|---|
| unigrams | 3,776 |
| unigrams-with_sw | 4,067 |
| bigrams | 18,534 |
| bigrams-with_sw | 23,667 |
| s-bigrams | 26,164 |
Table 3 contains an extract of the VSM with bigram, which corresponds to a
Table 3 Example of a vector in VSM with bigrams.
| { (70 2.2380), (288 2.2380), ... , (16821 0.8488), (18274 2.2380) } |
We also considered combinations of unigrams and unigrams-with_sw within other models as shown in Table 2. The numbers of features for the new models are shown in Table 4.
5.2. Construction of the LDA complement
Finally, for each Vector Space Model we generated new Vector Space Model complementing it with the results of the LDA algorithm. We used the values of 6, 50, 100, 500 and 1000 as the LDA parameter for the number of topics. In all cases the number of features of each LDA model directly corresponds to the number of topics, i.e., if the number of topics is 6 then the VSM is going to have only 6 additional features. In Table 5, we show an example of the LDA vector for the data from Table 3 using 6 topics. It is easy to see that the vector has non-zero value for the first topic only.
Table 5 Example of an LDA vector for data in Table 3.
| { Topic0 0.9934, Topic1 0.0, Topic2 0.0, Topic3 0.0, Topic4 0.0, Topic5 0.0 } |
In Table 6 we present only the best cases after the classification using Meka. We used the parameters and the values shown in Table 8. The LDA complement is represented as lda_n where n corresponds to the number of topics. Table 6 contains the proposed VSMs and their number of features. Classification results are presented in the next section.
Table 6 Size of the Vector Space Models with the LDA complement.
| Vector Space Model | Features |
|---|---|
| unigrams | 3,776 |
| unigrams + lda_6 | 3,780 |
| unigrams + lda_50 | 3,826 |
| unigrams + lda_100 | 3,876 |
| unigrams + lda_500 | 4,276 |
| unigrams + lda_1000 | 4,776 |
| bigrams | 18,534 |
| bigrams + lda_6 | 18,540 |
| bigrams + lda_50 | 18,584 |
| bigrams + lda_100 | 18,634 |
| bigrams + lda_500 | 19,034 |
| bigrams + lda_1000 | 19,534 |
| unigrams + bigrams | 22,310 |
| unigrams + bigrams + lda_6 | 22,316 |
| unigrams + bigrams + lda_50 | 22,360 |
| unigrams + bigrams + lda_100 | 22,410 |
| unigrams + bigrams + lda_500 | 22,810 |
| unigrams + bigrams + lda_1000 | 23,310 |
Table 7 An example of the vector with the LDA complement.
| { (70 2.2380), (288 2.2380), ..., (16821 0.8488), (18274 2.2380), (18533, 0.0), (18534 0.9934) } |
Table 8 Parameters of Meka.
| Parameter | Value |
|---|---|
| Multi-labeling algorithm | Rakel1 |
| Base classifier | Naïve Bayes |
| Validation method | k-Fold cross with k = 10 |
For example, for the vector shown in Tables 3 and 5, the result with the LDA complement is presented in Table 7. The LDA complement is marked in boldface, the features with zero values are not shown.
Each Vector Space Model was used in topic classification applying Meka with the parameters shown in Table 8.
6. Experiments
In this section, we present experimental results obtained using the proposed method and several baseline methods.
First of all, we build several VSMs based on traditional features and use them as the most obvious baseline method for comparison. Table 9 shows the results of the multi-labeling classification (Rakel1) using these VSMs ordered from the best case to the worst.
Table 9 F1 measure for traditional VSMs without combinations.
| Model | F1 measure |
|---|---|
| bigrams | 0.8970 |
| unigrams | 0.8955 |
| unigrams-with_sw | 0.8935 |
| bigrams-with_sw | 0.8800 |
| s-bigrams (syntactic) | 0.8405 |
Traditionally, it is considered that the best results in thematic classification are obtained using unigrams (i.e., words). As it can be seen, the baseline F1 measure for unigrams is 0.8955. Interestingly, the best case for our corpus is the use of bigrams without stop words, because its F1 measure value is 0.8970, though the difference between them is only 0.0015.
In Figure 4, we can see a comparative graphic with different F1 measures for various cases from Section 5.1.
On the other hand, Table 10 shows the results for classification using only the LDA model for the two best cases from Table 9. It is obvious that if we want to classify using only the LDA model, then our classification will be unsuccessful. The best case using LDA models is for unigrams with 100 topics with F1 measure of 0.6065, which is much worse than the results in Table 9 (0.8970 using bigrams).
Table 10 F1 measures for LDA only models from Table 6 using the best features from Table 9.
| LDA model | topics | F1 measure |
|---|---|---|
| unigrams | 100 | 0.6065 |
| unigrams | 50 | 0.5940 |
| unigrams | 100 | 0.5260 |
| unigrams | 6 | 0.5125 |
| bigrams | 100 | 0.5025 |
| unigrams | 500 | 0.4435 |
| bigrams | 50 | 0.4405 |
| bigrams | 6 | 0.4265 |
| bigrams | 500 | 0.4055 |
| bigrams | 1000 | 0.3920 |
Previously, we proposed considering combinations of different features to construct a new set of VSMs and classify using them. In Table 4, we presented the new features for different VSMs, Table 11 shows the different F1 measures for each VSM after the classification process.
Table 11 F1 measure for VSMs with single features.
| Model | F1 measure |
|---|---|
| unigrams + bigrams | 0.9180 |
| unigrams + bigrams-with_sw | 0.9120 |
| unigrams-with_sw + bigrams | 0.9120 |
| unigrams-with_sw + bigrams-with_sw | 0.9035 |
| unigrams + s-bigrams | 0.9025 |
| unigrams-with_sw + s-bigrams | 0.8975 |
We can see a slight improvement of the results. The difference between our baseline case and the best combination is 0.0225. In Figure 5 we present the comparative graphic for the used combinations of features.
Now, we can also consider combining different LDA models for the best case from Table 11. In Table 12 we present F1 measures being the best case 0.5870 using 50 topics. This value is very low as compared with 0.9180, which is obtained using a combination of unigrams and bigrams (both without stop words).
Table 12 F1 measure for the LDA models.
| LDA model | Topics | F1 measure |
|---|---|---|
| unigrams+bigrams | 50 | 0.5870 |
| unigrams+bigrams | 100 | 0.4605 |
| unigrams+bigrams | 500 | 0.4525 |
| unigrams+bigrams | 6 | 0.4355 |
| unigrams+bigrams | 1,000 | 0.3750 |
Finally, we propose using different LDA models combining them with the other VSMs. In this case, we choose the best cases in the previous experiments and our baseline case. In Table 13, we present the best results for the new VSMs.
Table 13 F1 measure for VSMs based on LDA complement.
| Model | F1 measure |
|---|---|
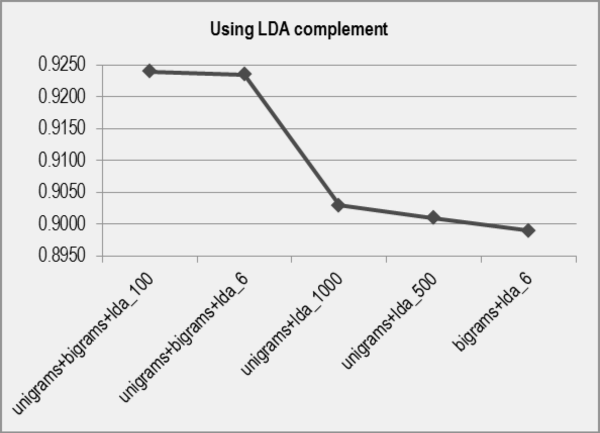
| unigrams + bigrams + lda_100 | 0.9240 |
| unigrams + bigrams + lda_6 | 0.9235 |
| unigrams + lda_1000 | 0.9030 |
| unigrams + lda_500 | 0.9010 |
| bigrams + lda_6 | 0.8990 |
It can be seen that the results are improved. The best case has F1 measure of 0.9240 and the value for our baseline case is 0.8955 being the difference 0.0285. The best value of 0.8970 which was obtained using traditional features is improved too being the difference of 0.0270.
The best case using the LDA complement improves the best case using combinations of features, being the F1 measure for the combinations 0.9180: the difference of 0.0060.
We can see that in some cases there is an improvement using the LDA complement, while in other cases there is no real improvement. All F1 measures using the LDA complement improve the F1 measures when we use only traditional features, but it is not so for the combinations of features. In Figure 6, we present the comparative graphic for the VSMs based on LDA complement.
Finally, in Table 14 we summarize the results for all experiments presented in this paper.
Table 14 Summary of all experimental values.
| Model | F1 measure |
|---|---|
| unigrams + bigrams + lda_100 | 0.9240 |
| unigrams + bigrams + lda_6 | 0.9235 |
| unigrams + bigrams | 0.9180 |
| unigrams + bigrams-with_sw | 0.9120 |
| unigrams-with_sw + bigrams | 0.9120 |
| unigrams-with_sw + bigrams-with_sw | 0.9035 |
| unigrams + lda_1000 | 0.9030 |
| unigrams + s-bigrams | 0.9025 |
| unigrams + lda_500 | 0.9010 |
| bigrams + lda_6 | 0.8990 |
| unigrams-with_sw + s-bigrams | 0.8975 |
| bigrams | 0.8970 |
| unigrams (baseline) | 0.8955 |
| unigrams-with_sw | 0.8935 |
| bigrams-with_sw | 0.8800 |
| s-bigrams | 0.8405 |
Figure 7 shows a comparative graphic for all experiments described in the previous sections. For the sake of clarity of the graphic we do not show the values on X axis (they are present on other graphics).
7. Conclusions and Future Work
In this paper, we considered the task of multi-labelled text classification. Experiments were conducted when we applied combination of various features (like bigrams and unigrams). The obtained results show certain improvements over baseline methods. Besides, we proposed to use a VSM complement based on the LDA, adding the LDA results as features to Vector Space Models. Our experiments showed that it allows improving the classification results for multi-label thematic text classification, giving the best F1 measure.
It is worth mentioning that the LDA model was used very successfully in classification for exactly one topic per document 13, but in case of multi-label classification the results of the LDA alone are very poor.
In our case, we assumed that if two documents are labelled with the same topics by LDA, then these documents really belong to the same topics. This is the reason why the LDA complement works for improving the results.
As it is mentioned in 12, 13, 19, 20, it is important to consider particular features for each topic during classification. In this sense, Latent Dirichlet Allocation is the method that allows finding these features for each topic. It is important to mention that we used various empiric values for a number of topics for the LDA algorithm. As future work, we plan to define the optimal number of topics that allows obtaining better results. We also plan to explore other methods based on LDA, for example L-LDA 10, and to verify other methods for dimensionality reduction such as latent semantic analysis (LSA).
Finally, the plan to try the ideas based on the soft similarity 8 applied to multi label classification. The soft similarity proposes to weight similarity of pairs of features in VSMs. For example, we can consider the similarity of topics using WordNet similarity of words that belong to each pair of topics.
