1. Introducción
La matriz insumo-producto es una forma de esquematizar el equilibrio de los sectores económicos que constituyen una economía de una ciudad o un país. Esto se obtiene desde la oferta y la demanda, teniendo como base el uso de los bienes y servicios; es sólo una descripción simplificada de una economía. Se puede utilizar para estudiar diversos temas, como la composición de valor agregado, el análisis de precios, calcular requerimientos de importaciones. Al mismo tiempo posibilita dar solución a preguntas tales como ¿cuáles son los sectores de mayor importancia relativa? y ¿qué sectores tienen la mayor articulación sectorial y las relaciones intrasectoriales?
Un gran referente en este campo es el trabajo de Leontief (1986), donde presenta un modelo insumo-producto con una característica especial: es un modelo simétrico, pero no en el sentido del álgebra lineal. Una matriz es simétrica, en el sentido de Leontief, cuando en sus filas y columnas se utilizan las mismas unidades, por la manera de construir las cuentas nacionales, en donde se distinguen entre sectores económicos y mercancías (ver Miller, 2009, caps. 4 y 5). Con relación a ella, algunos autores han mostrado una serie de elementos referidos a métodos e interpretaciones de ésta; se pueden destacar los trabajos de Chenery (1958), Rasmussen (1963) y Hirschman (1961). Los artículos seminales de las primeras aplicaciones de matrices regionales se pueden ver en Hirsch (1959), Isard y Kuenne (1953), Miller (1957) y Moore y Petersen (1955). De igual forma, para profundizar en esta área de matrices insumo-producto regionales existe una gran cantidad de trabajos que son publicados en revistas como Economic Systems Research, Journal of Regional Science, International Regional Science Review y Papers in Regional Science.
Ahora, de acuerdo con Blöch (2011), es natural interpretar la matriz insumo-producto como una red, en la que el vértice son los sectores, y el flujo de la actividad económica son las aristas; parte de la información se utiliza con el fin de vislumbrar sectores clave de la economía. De esta manera, se ha generalizado el uso de las redes de insumo-producto con el fin de hacer comparaciones entre diferentes economías (Blöch, 2011) o vislumbrar elementos regionales con matrices input-output multi-regionales (MRIO) (Cerina, 2015).
Al respecto, se pretende que la principal contribución de este trabajo sea la aplicación de la teoría de redes y de la matriz de Leontief en la economía de la ciudad de Medellín, mediante un análisis tradicional sobre encadenamientos productivos hacia adelante y hacia atrás de la matriz insumo-producto. También se intentan evaluar elementos coyunturales derivados del análisis de sectores que presentan importancia relativa, como el de energía eléctrica (que se puede considerar como indicador “adelantado o un termómetro” de una economía), que pueden ser vulnerables a choques negativos,1 hecho que afectaría el valor total del PIB de una economía regional. Con el fin de alcanzar el objetivo anteriormente descrito, este documento está organizado como se describe a continuación, siendo la primera sección esta introducción. En la segunda, se presenta la matriz insumo-producto y, además, se complementa con la teoría de redes insumo-producto. En la tercera y cuarta, se presenta el análisis de tipo empírico-exploratorio -que tiene como base las matrices de adyacencia construidas con el fin de calcular los diferentes indicadores- y sus resultados. En la quinta, se realizan simulaciones que pretenden evidenciar efectos sectoriales sobre el producto total, como se indicó anteriormente. Y, por último, se presentan las consideraciones finales.
2. Matriz insumo-producto
La matriz insumo-producto presenta una síntesis del equilibrio sectorial entre la oferta y la utilización de los bienes y servicios de una economía. En resumen, es una descripción sintética de la economía de un país o región. La matriz insumo-producto se compone de tres matrices: la primera, de demanda intermedia, permite ver los flujos de compras (columnas) y ventas (filas) entre sectores y consolida la actividad intermedia de la economía. La segunda, el valor agregado, muestra los pagos sectoriales al capital (contabilizado como excedente bruto de explotación) y al trabajo (remuneración a asalariados), para transformar los insumos en productos y los otros impuestos, menos los subsidios a la producción.
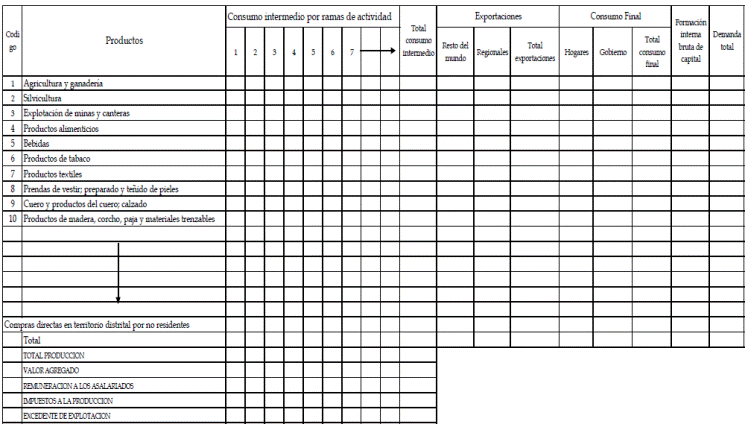
La tercera, de demanda final, representa las transacciones para el uso sectorial de los productos elaborados, en otras palabras, el consumo de los hogares, el consumo público, la inversión (representada en la formación bruta de capital fijo), y finalmente, las exportaciones. Un ejemplo muy sencillo del esquema insumo-producto se presenta en la Figura 1, donde se aprecia la capacidad de síntesis que se alcanza para plasmar la economía de una región o ciudad en una forma simple.
Asimismo, presentamos las ecuaciones fundamentales para entender la esencia de la matriz insumo-producto. Primero, la ecuación para la demanda:
Y segundo, la oferta:
Donde X ij representan las ventas realizada por el sector i al sector j, donde i, j = 1, 2, 3, … n (1=sector agricultura y ganadería, 2=sector silvicultura,...n=sector…). A su vez, D i representa la demanda final desde el sector i. Tal que X i es el producto del sector i, y X j , el total de entradas desde el sector j. Por último, VA j es igual a la remuneración de la producción de los factores. Por tanto, se puede evidenciar el coeficiente técnico del sector de la siguiente manera:
Para representar finalmente el problema de la siguiente manera:
Esto se puede mostrar en forma matricial, tal que:
También, debemos comprobar desde el principio la condición suficiente de la matriz productiva de Brauer-Solow, determinada por:
Donde la representación de la matriz es dada por:
Este sistema puede ser determinado si
Donde B ij son los coeficientes de la matriz y B es la matriz inversa de Leontief o las necesidades totales (directas o indirectas) que relaciona la producción de cada sector con la demanda final neta de importaciones consideradas como exógenas. Por lo tanto, los elementos de la matriz inversa cuantifican los impactos sobre un sector j (cualquier sector de la economía) a raíz de un cambio en la demanda final neta de las importaciones de un sector i (otro sector de la economía con relaciones con el sector j). Estos coeficientes recogen en un solo número efectos multiplicadores directos e indirectos, puesto que el producto de cada sector afectado no sólo se impacta a sí mismo, sino sobre otros sectores que lo utilizan como un insumo.
Hay una serie de supuestos implícitos en la matriz de insumo-producto que deben ser resaltados. En primer lugar, una hipótesis de homogeneidad sectorial: cada insumo es producido por un solo sector, que indica que cada uno de los sectores tiene una producción primaria o característica, pero no secundaria. En segundo lugar, una hipótesis de invarianza2 de los precios relativos: insumos o productos que tienen precios de valoración iguales para todos los productores. En tercer lugar, una proporcionalidad estricta: la composición de producto de cada sector se fija mostrando que las funciones de producción son lineales. Por lo tanto, los coeficientes técnicos serían constantes. Además, significa que la productividad marginal de cada factor es constante e igual, mostrando un promedio de rendimientos de escala constantes. Por último, una hipótesis de aditividad: esto básicamente propone que los efectos totales de la producción de diferentes sectores sean iguales a la suma total (Hernández, 2012). Sin embargo, existen algunas críticas, tales como no tener en cuenta la sustitución de los bienes; el supuesto de coeficientes técnicos fijos que imposibilita la producción bajo economías (o des-economías) de escala; y el tener en cuenta que los bienes de capital se encuentran en el vector de demanda y parecen no aportar a la productividad (Schuschny, 2005). A pesar de los elementos enunciados como críticos, la matriz insumo-producto es un instrumento de amplia utilización con el fin de vislumbrar las relaciones sectoriales de una economía.
2.1. Redes insumo-producto
Una matriz insumo-producto podría entenderse como un conjunto de vértices (sectores) conectados por una serie de aristas (relaciones entre sí). De esta forma, lograríamos utilizar la teoría de grafos, puesto que permite el estudio de consumos intermedios de la matriz insumo-producto, mostrando la representación de las relaciones sectoriales. Es así como un grafo es un par (v, a), donde v es el vértice (sectores) y a la arista (relaciones) que permite la representación de relaciones binarias entre los diferentes sectores. Consecuentemente, cuando dos vértices están conectados entre sí por más de un borde, entonces lo denominamos un multígrafo. Las relaciones entre los dos sectores concretos son dobles porque hay un flujo que va desde el sector i al sector j, y otra que va desde el sector j hasta el i. Si existe un vértice que se relaciona con sí mismo, sería denominado como pseudógrafo; éstos se hallan fácilmente en la matriz de consumos intermedios, debido a las diferentes relaciones intrasectoriales. No obstante, si por casualidad la dirección de la conexión entre dos vértices es relevante, como en los modelos de insumo-producto, entonces se tendría un diagrafo.3
Por lo demás, la trascendencia de la utilización de la teoría de grafos en un análisis de la teoría de insumo-producto se encuentra en la simplicidad y la capacidad de obtener resultados de gran interés. Pero esto no se considera como un sistema cerrado, ya que la suma total de las columnas y filas puede no ser los mismos. También, en las cuentas no se encuentran los diferentes componentes de la demanda autónoma (el consumo, la inversión, el gasto público y las exportaciones netas), de modo que en la representación gráfica de la matriz insumo-producto sólo se representan las compras y las ventas intermedias, es decir, sólo las relaciones intersectoriales o intrasectoriales (Blöch, 2011).
2.2. Metodología
La propuesta metodológica se realiza pensando en las enormes posibilidades de estudio que ofrece la matriz insumo-producto. La cualidad más importante de la matriz es la posibilidad de resumir o ponderar los términos de intercambio (circular) entre los sectores, como los proveedores de insumos intermedios y demandantes. Adicionalmente, posibilita la caracterización de los sectores cuya importancia relativa es significativa.
Consecuentemente, la matriz utilizada es la insumo-producto de Medellín 2010. La principal circunstancia para elegir este enfoque obedece a la idea de corroborar que todos los sectores económicos carecen de la misma capacidad de causar impactos multiplicadores pertinentes sobre otros. Es decir, hay sectores económicos que por su estructura y magnitud son auténticos impulsores del crecimiento económico; y también encontramos el otro extremo, sectores que son rezagados dentro de la estructura productiva regional. No obstante, vamos a utilizar un enfoque diferenciado basado en la selección de la matriz de adyacencia. Así que, en primer lugar, vamos a utilizar una matriz de adyacencia con base en las matrices a o b de lo anteriormente enunciado.
3. Matriz de adyacencia A
3.1. Los enlaces directos
Diversos autores recurren a vínculos sectoriales4 para analizar los cambios en la demanda final, y con esto poder desentrañar sectores relevantes para una economía (ver Chenery, 1958; Hirschman, 1961; y Rasmussen, 1963). Se tiene que los encadenamientos hacia atrás evalúan la capacidad de un sector para obtener el desarrollo de otros sectores, ya que utilizan insumos procedentes de dichos sectores. Por otra parte, los encadenamientos hacia adelante se producen cuando un sector ofrece su producción, que resulta ser el insumo de otro sector, que de la misma manera estimula el tercer sector que está en el extremo de la producción desde el primer sector mencionado. A su vez, Chenery (1958) calcula los indicadores directos hacia atrás y hacia adelante con base en los coeficientes técnicos de la matriz. En este caso, tenemos que los eslabonamientos directos hacia atrás serán:
Y los encadenamientos directos hacia adelante serán: DFLi= a
Asimismo, en lo que respecta a DFL i y DBL j , los sectores son clasificados como se muestra en la Tabla 1, donde: (I) No manufacturero/Destinación intermedia: sectores que venden a otros cantidades importantes de su producción, y por eso poseen altos encadenamientos hacia adelante y bajos hacia atrás; corresponden a sectores de producción primaria intermedia. (II) No manufacturero/Destinación final: no compran significativamente a los demás sectores, razón por la cual se consideran de producción primaria; adicionalmente, no venden una gran cantidad de insumos a otros sectores. (III) Manufacturero/Destinación final: sectores que compran a otros sectores cantidades importantes de insumos, pero la mayor parte de su producción se dirige a la demanda final. (IV) Manufacturero/Destinación intermedia: sectores que compran cantidades importantes de insumos, y venden su producción a otros sectores (Schuschny, 2005).
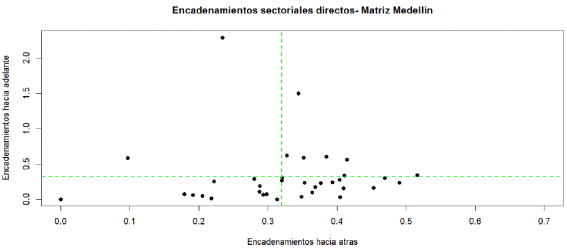
La Figura 2 es una representación de los vínculos directos que muestra la producción regional de la ciudad de Medellín, Colombia. De acuerdo con esta figura, se puede afirmar que es básicamente no manufacturera de destino final y manufacturera de destino final. Por lo tanto, los sectores predominantes en la economía de la región se podrían separar en dos grupos: el primer grupo son sectores con pocos encadenamientos directos hacia atrás y hacia adelante. El segundo grupo son sectores que tienen mayores encadenamientos hacia atrás y bajos hacia adelante, donde sería más fácil la aparición y propagación de choques de la demanda.
3.2. Redes de matriz binaria
En este caso, hemos diseñado una matriz binaria soportada sobre la teoría de grafos que tiene como base la matriz de insumo-producto. Así, cada relación sectorial tendrá una explicación en términos de la existencia de la relación y no del peso relativo, teniendo entonces lo que se muestra en la Tabla 2.
Tabla 2 Resultados del análisis de las métricas.
| Graph Metric | Value |
|---|---|
| Vertices | 35 |
| Unique Edges | 870 |
| Self-Loops | 32 |
| Connected Components | 2 |
| Single-vertes Connecter Components | 1 |
| Maximum Vertices in a Connected Componente | 34 |
Fuente: Elaboración propia creada con NodeXL.
El número de sectores que se tienen en cuenta en el ejercicio son 35, en el cual las relaciones totales de los sectores son 870. Al respecto, observamos que cada sector se relacionó en promedio con aproximadamente 24 sectores. Esto nos permite afirmar que la interdependencia de los diferentes sectores de la economía de Medellín es normal, lo que significa una relación con más de la mitad de todos los sectores. Los sectores que tienen mayores relaciones tuvieron relaciones comerciales con otros 34 sectores, además se destaca que existen alrededor de 32 relaciones intrasectoriales.
De esta forma, podríamos vislumbrar las interrelaciones entre los sectores y los recursos (insumo) con el fin de vislumbrar sectores clave o estratégicos de la economía en relación con el número de sectores relacionados, tanto en lo referente a las compras como a las ventas. Los sectores con mayores encadenamientos hacia adelante se muestran en la Figura 3. Y los sectores con mayores eslabonamientos hacia atrás directos se muestran en la Figura 4.

Fuente: Elaboración propia. Created with NodeXL (http://nodexl.codeplex.com)
Figura 3 Eslabonamientos directos hacia adelante de Medellín.
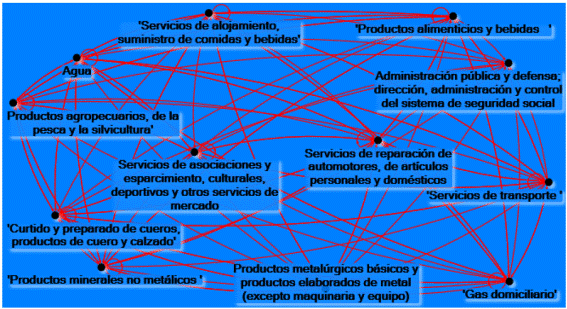
Fuente: Elaboración propia. Created with NodeXL (http://nodexl.codeplex.com)
Figura 4 Eslabonamientos directos hacia atrás de Medellín.
4. Matriz de adyacencia B
4.1. Vínculos directos e indirectos
En este campo, Rasmussen (1963) reconoce la importancia de los encadenamientos entre las diferentes industrias, e incorpora la importancia de los efectos de difusión o dispersión de un choque económico, es decir, del grado en que un sector puede afectar más o menos sectores, independientemente del tamaño del encadenamiento. El valor BL j* es el eslabonamiento total hacia atrás desde el sector j, e indica cómo el producto de todos los sectores aumenta (o disminuye) tan pronto como las demandas finales netas de las importaciones procedentes del sector j aumentan (o disminuyen) en una unidad:
Y en los encadenamientos totales hacia adelante (FL i* ), cada valor indica en cuánto debe aumentar (o disminuir) el producto del sector i, si la demanda final neta de las importaciones procedentes de todos los sectores aumenta (o disminuye) en una unidad. Así, no sólo se mide la manera en que el sector se ve afectado por la expansión de la demanda final unitaria de todos los sectores, sino también la dependencia que todos los sectores tienen con el sector i (Schuschny, 2005):
En el Tabla 3 están los encadenamientos totales. Se realizan sobre la inversa de la matriz de Leontief (B). Para el caso de Medellín corresponde a 35 sectores estudiados en la economía de la ciudad. Éstos son una representación de los sectores con vínculos directos e indirectos totales hacia adelante y hacia atrás. Uno de los sectores que mayores eslabonamientos sectoriales posee es el sector Comercio, en el que, por cada 100 pesos adicionales en la demanda del sector, sus encadenamientos producen un incremento de 148.9 pesos en la demanda total de la economía, 34.4 pesos de ellos debido a un efecto directo y 114.5 debido a un efecto indirecto. Desde el lado de la oferta, ese incremento de 100 pesos en la demanda induce un incremento de 302.1 pesos en la oferta, de los cuales 150.1 pesos serán por un efecto directo y 152 pesos serán por efecto indirecto. De igual forma, se realiza el análisis con todos los sectores, con el fin de establecer cuáles tienen un mayor efecto multiplicador hacia la demanda o hacia la oferta, lo cual permite inferir elementos de política sectorial diferenciados para estimular los sectores (ver Hernández, 2012).
Tabla 3 Sectores y sus eslabonamientos sectoriales.
| Directos | Totales | |||
|---|---|---|---|---|
| Sector | Oferta | Demanda | Oferta | Demanda |
| Productos agropecuario, de la pesca y la silvicultura | 7,4 | 29,8 | 109,6 | 145,7 |
| Productos de la minería | 4,5 | 20,5 | 105,2 | 131,0 |
| Productos alimenticios y bebidas | 27,3 | 40,4 | 133,8 | 159,9 |
| Productos textiles | 26,1 | 32,0 | 133,9 | 146,0 |
| Tejidos de punto y ganchillo; prendas de vestir | 17,6 | 36,8 | 125,9 | 153,2 |
| Curtido y preparado de cueros, productos de cuero y calzado | 16,2 | 45,3 | 119,5 | 168,6 |
| Productos de madera, corcho, paja y materiales trenzables | 24,0 | 39,3 | 133,0 | 159,8 |
| Productos de papel, cartón y sus productos | 33,6 | 41,1 | 148,5 | 162,2 |
| Edición, impresión y artículos análogos | 9,6 | 36,4 | 115,5 | 153,8 |
| Sustancias y productos químicos | 60,0 | 38,5 | 183,0 | 157,5 |
| Productos de caucho y de plástico | 22,9 | 37,7 | 134,0 | 156,4 |
| Productos minerales no metálicos | 18,7 | 28,8 | 124,9 | 141,0 |
| Productos metalúrgicos básicos y productos elaborados de metal (excepto maquinaria y equipo) | 30,3 | 46,9 | 137,6 | 171,6 |
| Maquinaria y equipo | 11,0 | 28,8 | 112,8 | 143,0 |
| Otra maquinaria y suministro eléctrico | 6,5 | 29,3 | 108,3 | 142,9 |
| Equipo de transporte | 3,0 | 40,4 | 104,0 | 158,3 |
| Otros bienes manufacturados n.c.p. | 30,6 | 32,0 | 149,4 | 147,5 |
| Energía eléctrica | 59,2 | 35,2 | 198,3 | 152,9 |
| Gas domiciliario | 3,5 | 34,9 | 104,7 | 149,7 |
| Agua | 5,9 | 19,1 | 107,5 | 127,2 |
| Servicios de alcantarillado y eliminación de desperdicios, saneamiento y otros servicios de protección del medio ambiente | 7,2 | 17,9 | 110,6 | 125,7 |
| Trabajos de construcción | 28,9 | 28,0 | 137,0 | 141,0 |
| Comercio | 150,1 | 34,4 | 302,1 | 148,9 |
| Servicios de reparación de automotores, de artículos personales y domésticos | 25,0 | 22,2 | 145,9 | 132,4 |
| Servicios de alojamiento, suministro de comidas y bebidas | 15,4 | 41,0 | 124,7 | 159,1 |
| Servicios de transporte | 56,0 | 41,5 | 188,7 | 160,3 |
| Servicios de correos y telecomunicaciones | 34,3 | 51,6 | 159,9 | 176,7 |
| Servicios de intermediación financiera, de seguros y servicios conexos | 62,2 | 32,7 | 202,6 | 146,1 |
| Servicios inmobiliarios y de alquiler de vivienda | 58,6 | 9,7 | 194,7 | 113,5 |
| Servicios a las empresas excepto servicios financieros e inmobiliarios | 228,7 | 23,4 | 446,6 | 133,5 |
| Administración pública y defensa; dirección, administración y control del sistema de seguridad social | 0,0 | 31,3 | 100,0 | 145,1 |
| Servicios de enseñanza de mercado | 1,2 | 21,8 | 101,5 | 129,9 |
| Servicios sociales y de salud de mercado | 23,5 | 49,0 | 130,8 | 178,5 |
| Servicios de asociaciones y esparcimiento, culturales, deportivos y otros servicios de mercado | 23,6 | 35,3 | 136,3 | 151,7 |
| Servicios domésticos | 0,0 | 0,0 | 100,0 | 100,0 |
Fuente: Elaboración propia.
Para este trabajo es de particular interés los sectores de Energía eléctrica; Curtido y preparado de cueros, productos de cuero y calzado; Productos alimenticios y bebidas, y Trabajos de construcción. Este hecho se explica por elementos coyunturales, tales como posibles choques negativos pronosticados, su alto valor agregado y su importancia como grandes generadores de empleo. Además, el encadenamiento total hacia atrás (demanda) de estos sectores produce un aumento de la demanda mayor a 100 pesos. A su vez, estos sectores también tienen una fuerte respuesta desde el lado de la producción. Por lo tanto, se consideran sectores clave para realizar un ejercicio de impulso respuesta, con el fin de conocer qué pasaría en la economía si estos sectores se vieran afectados por alguna circunstancia.
5. Simulaciones
Teniendo en cuenta las diferentes relaciones intersectoriales e intrasectoriales determinadas a través de los eslabonamientos sectoriales hacia adelante y hacia atrás, se genera un ejercicio de simulación, tomando como base los sectores de Trabajos de construcción; Energía eléctrica, Curtido y preparado de cueros, productos de cuero y calzado, y Productos alimenticios y bebidas.
En especial, nos referimos al choque de energía, ya que el sector eléctrico cuenta con una capacidad instalada de 15.489 MW, donde la hidroelectricidad aporta un 70% de la bolsa total de energía. Sin embargo, en periodos de alta sequía, como el fenómeno del Niño,5 es muy probable que según su intensidad sea necesario recurrir a operar plantas de respaldo como las de energía térmica (gas o combustibles), hecho que conlleva mayores costos. Es así como en el ejercicio realizado se simula un choque negativo en la demanda de energía del 1%, teniendo como base una inercia del choque de 0.95, es decir que a la demanda sólo se le aplica un choque por un periodo, pero se presenta una inercia alta al fenómeno representado, permaneciendo lo demás constante (hecho que será común a los demás sectores que se simulan). De esta forma, en el vector de demanda sólo se afecta la demanda del sector objeto del choque y se simula la trayectoria del producto total de la economía derivada de este choque. Luego se representan las diferencias con respecto al periodo base, es decir, se presenta la trayectoria de desviación del Valor Bruto de la Producción del sector (producto) con respecto al año base (ver Figura 4). Y con base en los resultados se calcula el valor del PIB de la ciudad de Medellín que se puede ver afectado por estos choques negativos, de no tomarse las medidas pertinentes para evitar reducciones en la demanda de los sectores analizados.
Por su parte, la simulación del sector de la construcción (ver Figura 5) obedece a la importancia estratégica que se le ha brindado a este sector desde los años setenta con el Plan de las Cuatro Estrategias,6 y todos los elementos vinculados a éste, tales como su capacidad de generar una cantidad muy elevada de empleos de mano de obra no calificada y la serie de elementos que se vinculan a sus eslabonamientos sectoriales hacia adelante y hacia atrás.
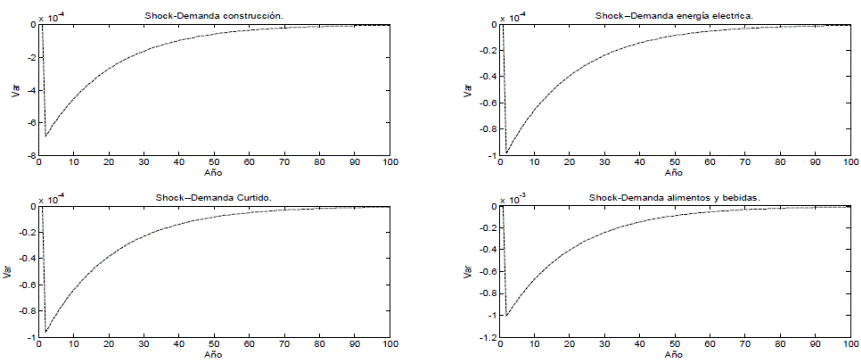
Fuente: Elaboración propia.
Figura 5 Impulso respuesta del producto de Medellín ante un shock negativo del 1% en la demanda de diferentes sectores.
Con respecto a los sectores de Curtido y preparado de cueros, productos de cuero y calzado, y Productos alimenticios y bebidas, se tiene que la importancia de su simulación se deriva de que son sectores que tenían una importancia estratégica dentro de las exportaciones que la economía regional realizaba a Venezuela, y que se ha visto disminuida por la política comercial aplicada en los últimos años. Por consiguiente, su importancia se encuentra explicada por el hecho de que son bienes que tienen alto valor agregado y cuyas ventas al país vecino se han visto disminuidas por la coyuntura negativa en las relaciones comerciales con este país. Los resultados son presentados en la Figura 5.
Los resultados muestran que una reducción en la demanda del 1% en los sectores de Trabajos de construcción, Energía eléctrica, Curtido y preparado de cueros, productos de cuero y calzado, y Productos alimenticios y bebidas generan una variación negativa en la producción total de la economía de Medellín de aproximadamente el 0.06, 0.01, 0.009 y 0.10%, respectivamente.
Partiendo del hecho de que el sector de Trabajos de construcción tiene relaciones con 17 sectores hacia adelante y con 26 sectores de eslabonamientos hacia atrás y su efecto multiplicador total de demanda es de 1.41 y de oferta es 1.37 en la economía por cada peso de demanda, se nota claramente que una reducción de esta actividad afectaría de manera significativa la dinámica económica de la región.
Con respecto al sector de la Energía Eléctrica, se afectaría a 34 sectores con eslabonamientos hacia adelante y a 26 por sus relaciones de eslabonamientos hacia atrás. El efecto multiplicador directo de este sector es de 59.2 y 35.2 por oferta y demanda, respectivamente; y el multiplicador total es de 198.3 y 152.9, respectivamente, por cada 100 pesos. En consecuencia, se muestra claramente la vulnerabilidad de la región ante shocks negativos de oferta o demanda en este sector estratégico dentro de la economía, ya que anteriormente se consideraba un indicador adelantado.
Con respecto a los sectores de Curtido y preparado de cueros, productos de cuero y calzado, y Productos alimenticios y bebidas, éstos se encuentran relacionados con 28 y 29 sectores por el lado de la oferta, y con 16 y 17 por el lado de la demanda, respectivamente. Los multiplicadores directos de estos sectores son 16.2 y 27.3 por oferta y 45.3 y 40.4 por demanda; y los multiplicadores totales son de 119.5 y 133.8 por oferta, respectivamente, y de 168.6 y 159.9, respectivamente, por cada 100 pesos de demanda. Los resultados muestran que el sector de Productos alimenticios y bebidas tiene mayores efectos dentro de la economía de Medellín y, por ende, debe gozar de especial atención, con el fin de evitar choques negativos de oferta o demanda.
6. Consideraciones finales
Es importante destacar que la economía de Medellín a nivel sectorial es productora de bienes no manufactureros de destino final y manufactureros de destino final; lo cual nos lleva a pensar en políticas sectoriales regionales que nos permitan superar los umbrales y llevar la economía a un nivel de desarrollo más elevado, donde nos deberíamos encontrar en mayor proporción con bienes de alto valor agregado.
Las relaciones sectoriales de la región vislumbran un elemento interesante, concerniente al sector de la construcción, pues se encontró que no es un sector con altos eslabonamientos sectoriales hacia adelante ni hacia atrás, hecho que está corroborado a nivel nacional por el trabajo de Hernández (2012), donde, por medio de una matriz insumo-producto de Colombia, muestra unos multiplicadores totales de demanda de 115.07 para este sector, hecho muy cercano a los valores encontrados para Medellín. Sin embargo, la caída de su demanda muestra grandes efectos dentro del producto total de la economía.7 Además, es importante destacarlo como un sector generador de empleos, ya que, según el DANE (2015), en el trimestre julio-septiembre de 2015 generó 120,734 empleos directos en la ciudad de Medellín, representando un 6.7% del empleo total de la ciudad, y 1,404,464 de empleos a nivel nacional, representando un 6.1% de los empleos generados en octubre de 2015.
Se debe colocar especial atención a los sectores de Curtido y preparado de cueros, productos de cuero y calzado, y Productos alimenticios y bebidas, ya que muestran ser sectores con grandes relaciones intersectoriales que pueden generar mayores dinámicas a la economía regional. Además, es importante que se generen las medidas pertinentes con el fin de blindar la economía con respecto a una reducción en la oferta de energía, ya que sus efectos serían bastante adversos para la economía regional.











 nueva página del texto (beta)
nueva página del texto (beta)