Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ciencias forestales
versão impressa ISSN 2007-1132
Rev. mex. de cienc. forestales vol.9 no.48 México Jul./Ago. 2018
https://doi.org/10.29298/rmcf.v8i48.130
Articles
Cultivation shifts in forest plantations of Eucalyptus grandis Hill ex Maiden, in Uruapan, Tabasco
1Posgrado en Desarrollo Económico Local. Universidad Autónoma de Nayarit. México.
2Escuela de Economía y Finanzas. Universidad Autónoma de Guadalajara. México.
3División de Ciencias Económico-Administrativo. Universidad Autónoma Chapingo. México.
4Gerencia de Desarrollo y Transferencia de Tecnología. Comisión Nacional Forestal. México.
Commercial timber plantations in Mexico have become an opportunity for increasing the production and productivity of the subsector, as well as for reducing the pressure on the natural forest areas and increasing the income of rural families. The objective of this research was to analyze the relationship and behavior between three different types of shifts: 1) Technical: Maximum Average Production (MAP) and Maximum Total Production (MTP); 2) Economic: Hotelling and Faustmann; and 3) economic-environmental: Hartman- in plantations of Eucalyptus grandis in the municipality of Balancán, Tabasco, Mexico, and to provide elements that may contribute to decision-making in the forestry companies. Data from three inventories provided by the company Productora de Plantaciones del Sureste were used. The type of average interest rates of the certificates of the Treasury of the Federation (CETES) (8 %), an average price of $107.00 tCO2e-1 (tab average used by the European Climate Exchange Carbon from 2010 to 2014), a cost of establishment of the planting of $38 000 ha-1, a price of roundwood of $650.00 m-3, and a cost of $2 000.00 ha-1 yr-1 were considered. The estimated shifts were the following: MAP (10.24 years), Faustmann (10.82 years), Hotelling (11.32 years), Hartman (11.64 years) and MTP (97.2 years). We conclude that the number of years increases as economic-environmental aspects are incorporated in the estimation of shifts.
Keywords: Carbon capture; forestry companies; Schumacher growth model; economic shifts; environmental-economic shifts; technical shifts
Las plantaciones forestales maderables comerciales en México se han convertido en una oportunidad para incrementar la producción y productividad del subsector, así como para disminuir la presión sobre las zonas forestales naturales y aumentar los ingresos de las familias rurales. La presente investigación tuvo como objetivo, analizar la relación y el comportamiento existente entre tres tipos de turnos: 1) técnicos: Máxima Producción Media (MPM) y Máxima Producción Total (MPT); 2) económicos: Hotelling y Faustmann; y 3) económico-ambiental: Hartman, en plantaciones de Eucalyptus grandis ubicads en el municipio Balancán, Tabasco, México; y aportar elementos que contribuyan a la toma de decisiones en las empresas forestales. Se utilizaron los datos de tres inventarios proporcionados por la empresa “Productora de Plantaciones del Sureste”, se consideró el tipo de interés promedio de Certificados de la Tesorería de la Federación (Cetes) (8 %), un precio promedio del carbono de $107.00 tCO2e-1 (tabulador promedio usado por European Climate Exchange Carbon de 2010 a 2014), un costo de establecimiento de la plantación de $38 000 ha-1, un precio de la madera en rollo de $650 m-3 y un costo de renta de tierra $2 000 ha año-1. Los turnos estimados fueron los siguientes: MPM (10.24 años), Faustmann (10.82 años), Hotelling (11.32 años), Hartman (11.64 años) y MPT (97.2 años). Se concluye que a medida que se incorporan aspectos económico-ambientales en la estimación de los turnos, se observa un alargamiento o incremento en el número de años.
Palabras clave: Captura de carbono; empresas forestales; modelo de crecimiento tipo Schumacher; turnos económicos; turno económico-ambiental; turnos técnicos
Introduction
With the incorporation of Mexico to the General Agreement on Tariffs and Trade (GATT) in 1986 and the entry into force of the North American Free Trade Agreement (NAFTA) in 1994, the pressures on the country’s natural resources increased. Authors such as Barton and Merino (2004) speculate that these have been factors that contribute to the deterioration of forest resources. However, they are not exclusive of free trade; there are causes that go beyond commercial exchanges -e.g. poor forest management plans, the growing urban sprawl, the increase in agricultural land and pastures for livestock, and illegal logging.
Historically, the timber production in Mexico comes from natural forests (Álvarez et al., 2015; Luján et al., 2016); on average, during the period of 1990 to 2014, 84 % of the production came from coniferous forests, 11 percent, from broadleaf forests, and 5 %, from tropical forests (Semarnat, 2014). This is why special attention was given to the estimation of biological or technical shifts (Semarnat, 2010).
In 1995, the establishment of commercial timber plantations (CTPs) was encouraged with the three-fold purpose of increasing the production and productivity of the raw materials subsector, reducing the pressure on the natural forest areas, and increasing the income of rural households (Luján et al., 2016). Moreover, they emerged as a productive option to convert agricultural land that had lost its vegetation into forest land capable of producing raw materials to supply the forest industry and provide ecosystem services (Conafor, 2016). Andreoni and Bussoni (2014) point out that the growing demand for timber products can be addressed by means of an adaptive strategy through genetic improvement in plantations.
On the other hand, with the implementation by CONAFOR of the National Strategy of Sustainable Forest Management to increase the production and productivity (Enaipros) 2013-2018 and of the National Strategy for REDD+ (Reducing Emissions from Deforestation and Forest Degradation), one of the greatest challenges is to increase the forest timber production and to reduce the emission of greenhouse gases; therefore, CTPs are considered to be a viable option for the achievement of these objectives (Geréz and Pineda, 2011; Conafor, 2016).
The implementation of both strategies has promoted the establishment of CTPs of fast-growing tropical species such as Tectona grandis L. F., Gmelina arborea Roxb., Cedrela odorata L., and Eucalyptus grandis Hill ex Maiden (Conafor, 2016). This brought about the need for viable forest shifts according to the current necessities (technical, economic shifts and economic-environmental).
The application of the theory of the economically optimal shift in CTPs has not been addressed with sufficient profusion by the forestry literature of Mexico. Authors such as Medema and Lyon (1985), who wrote one of the first papers that dealt with the issue, applied Faustmann’s formulation and solution, proposed in 1849, using an iterative procedure for the calculation of the optimal age. Tait (1986), Chang (1998), and Smart and Burgess (2000) utilized the formulation with a generalized solution, using dynamic programming. As for the forest shifts, which incorporate as input the timber production and carbon capture, they have been cited since the 1990s (Hoen and Solberg, 1994; Van et al., 1995; Romero et al., 1998).
Although, studies of forest shifts have been carried out at the international level, the basic issues of forest management and exploitation in Mexico revolve around the few efforts made to research appropriate shifts and, to a greater extent, for the State of Tabasco, despite its being one of the main entities with CTPs (Conafor, 2016).
This research posed the following hypothesis: as environmental aspects are incorporated in the estimation of the economic shifts, the optimal felling age is greater, resulting in a lengthening in the number of years of the forest shift. The objective was to analyze the behavior and the relationship between three types of forest shifts in commercial plantations of Eucalyptus grandis Hill ex Maiden located in Balancán, Tabasco, Mexico, by calculating three shifts -technical, economic and environmental-economic-, as well as to provide elements that may contribute to decision-making in the forestry companies.
Materials and Methods
Study area
The study area is located in the municipality of Balancán in the Usumacinta region of Tabasco, Mexico. It is located at the coordinates 17°48' N and 91°32' W. It borders Campeche to the north, the municipalities Tenosique and Emiliano Zapata to the south, the state of Campeche and the Republic of Guatemala to the east, and the municipality of Emiliano Zapata and Campeche to the west (Municipios.mx, 2016) (Figure 1).
Adjusted growth model
A Schumacher growth model relating the volume of wood to age and assuming that the rate of growth varies inversely with age, was adjusted (López and Valles, 2009).
Where:
V(t)= Volume of timber in the year t (m3tree-1)
t = Age (years)
βi = Parameters, to i = 0 and 1
Forest shifts
Five forest shifts were estimated: two technical shifts (maximum total production and maximum average production), two economic shifts (Hotelling 1931, and Faustmann 1849) and one economic-environmental shift (Hartman, 1975). The last three were based on the determination of the monetary value of the timber production, as suggested by Romero et al. (1998).
Technical shifts. The technical approach involves a bare analysis, due to its low complexity for manipulating the growth or the production function. The maximum total production occurs at the highest point of the production function; thus, the optimal felling shift is when the marginal production is equal to zero. Likewise, the maximum average production is obtained by dividing the production function by the age of the plantation (t) (Bonilla and Alarcón, 2015).
Economic Shifts. In forest economy and management this is a concept that incorporates economic aspects such as production costs, timber prices and interest rate. Given their theoretical and practical importance, two economic shifts were analyzed: Hotelling’s formulation of 1931, and Faustmann’s approximation of 1849 (Díaz, 1997).
The procedure suggested by Hotelling consists in maximizimg the Current Net Value (CNV) of the investment:
Where:
p = Price of timber (MXN)
V(t) = Volume of timber in the year t (m3 tree-1)
i = Type of discount
t = Age (years)
k = Cost of the plantation (MXN tree-1)
Therefore, the condition of balance of Eq. 2 is given by the following expression.
Where:
V´(t)= Marginal timber product in the year t
The model suggested by Faustmann includes a land rent variable; thus, the expression Eq. 2 becomes:
Where:
R = Land rent (MXN)
dt = Age differential
and the condition of balance of Eq. 4 is:
Environmental-economic shift. The basic idea of Hartman is to introduce a function G(t) that measures the flow of non-timber (environmental, recreational, or ecosystem) services or income generated by a forest mass with an age of t years, in addition to the production curve V(t) (Romero, 2001). The Hartman model posed is:
Where the condition of balance is given by:
The non-timber yield curve suggested by Hartman is a production function in which the marginal productivities may decrease but are never negative. The function G(t) is calculated based on the value of the carbon captured in the plantation.
Estimation of carbon capture
The accumulated (captured) carbon per hectare was estimated in terms of the volumetric yield, based on the amount of carbon per m3 of wood. The density of the wood and the carbon content of biomass estimated with the procedure of Smith et al., (1993) were considered.
The amount of CO2e (carbon equivalent) of Table 1 includes only the carbon contained in the biomass of the stem; that of the branches and foliage was calculated using conversion factors of total aerial biomass, based on the biomass of the stem. The production of biomass of the stem in relation to the total area for Eucalyptus grandis Hill ex Maiden was 88 %; therefore, the conversion factor was: 100/88=1.136. Thus, the total amount of CO2e per m3 of timber was 0.919 tonnes.
Table 1 Estimation of carbon capture by Eucalyptus grandis Hill ex Maiden.
| Variable | Eucalyptus grandis |
|---|---|
| Density (t m-3) | 0.46 |
| Content of carbon in biomass (percentage in decimal form) | 0.48 |
| Carbon/volume ratio (tC m-3) | 0.46 × 0.48 = 0.22 |
| CO2e/timber volume ratio (tCO2e m-3)† |
|
Source: Téllez et al. (2008).
† = CO2 equivalent; †† = 44 corresponds to the molecular weight of CO2, and 12 to the molecular weight of C.
The value of the benefits obtained from carbon capture G(t) was estimated using the approach of Van et al. (1995) as modified by Stainback and Alavalapati (2002):
Where:
G(t)= Net value of the benefits from carbon capture (MXN)
πco2Tot = Total value of the standing tree due to carbon capture (MXN)
πco2Des = Value discounted due to the harvested timber products (MXN)
p c = Price of carbon ($/tCO 2 e)
α = Constant expressing the proportion of CO2e per m3 of timber
V(t)= Volume of timber in the year t (m3 tree-1)
i = Type of discount
t = Age (years)
dt = Age differential
β = Discounted proportion of the harvested timber
A value equal to β 0.10 was considered; i.e. 10 % of the captured carbon is released in the whole process of harvesting and sawmilling.
Provenance of the information
Data from three national forest inventories (2009, 2010 and 2011) carried out by the company "Productora de Plantaciones del Sureste" (Proplanse) in plantations of Eucalyptus grandis in the municipality of Balancán, Tabasco, Mexico, were used in the present research. A random stratified sampling design was utilized, and sites of fixed dimensions were defined as sampling units. The equation for cubing standing trees, which is a modification to the Australian model, was obtained from Proplanse.
Where:
V = Volume in cubic meters without the bark (m3)
d = Normal diameter in meters (m)
a = Total tree height in meters (m)
The average interest rate or discount provided by the certificates of the Treasury of the Federation (CETES) (8 %) and an average price of carbon of $107.00 per tonne of CO2e (average tabulator utilized by European Climate Exchange Carbon from 2010 to 2014) were considered. The data related to the cost of the plantation ($38 000 ha-1, MXN), the price of wood ($650 m-3, MXN) and the rent of land ($2 000 ha-1 year-1, MXN) were provided by the company Proplanse.
Results and Discussion
The Schumacher production function was formulated based on the results of this study.
The production function shows a high correlation coefficient (R2 = 0.9989), which is indicative of an adjustment, as well as low levels of Sum of Squares of the Error (SCE = 0.00062).
Technical shifts. The Schumacher-type function has a horizontal asymptote, which implies that it does not decrease. To this end, we obtained an approximation by discriminating 10 % of the total production, since the marginal increases are minimal, as shown:
Where:
α = Percentage of production for discrimination (10 % in this study)
By solving this equation and replacing in the production function (Eq. 9), the Maximum Total Production (MTP) is shown to be attained at 97.20 years of age of the plantation. The Schumacher production function turned out to be an inappropriate model for the calculation of the MTP, whereas the adjusted model allows projecting it 25 % into the future, according to Montgomery et al. (2007); i.e. it predicts acceptably up to the 19th year (the information presented is indicative).
The Maximum Average Production (MAP) corresponds to 10.24 years of age of the plantation (Figure 2).
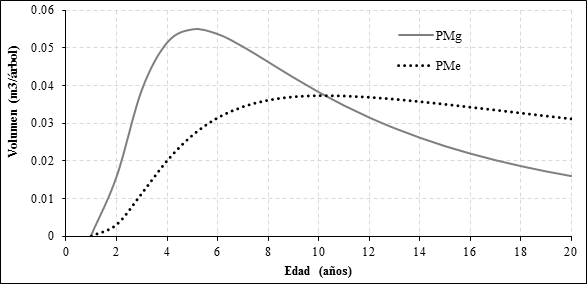
Volumen = Volume; Edad = Age
Figure 2 Marginal Production Curves (PMg) and Mean Product (PMe) for Eucalyptus grandis Hill ex Maiden, derived from the adjusted Schumacher function.
Economic shifts. Once the economic values in the formulations of Hotelling and Faustmann had been replaced, the balance curves were calculated for each formulation, being of 11.32 years for Hotelling’s shift, and 10.82 years for Faustmann’s (Figure 3, Table 2).

VAN = CNV (Current Net Value); Edad = Age
Figure 3 Hotelling, Faustmann and Hartman equilibrium curves for Eucalyptus grandis Hill ex Maiden, derived from the adjusted Schumacher function.
Table 2 Overview of the forest shifts estimated for Eucalyptus grandis Hill ex Maiden.
| Shifts | Type | Forest shift (years) |
|---|---|---|
| Technical | Maximum total production | 97.20 |
| Maximum average production | 10.24 | |
| Economic | Hotelling | 11.32 |
| Faustmann | 10.82 | |
| Economic-Environmental | Hartman | 11.64 |
Environmental-economic shift. The balance function, whose shift is reached at 11.64 years of age, was calculated by integrating the economic and environmental values (Figure 3, Table 2).
The estimated forest shifts constitute a novel contribution to investors both in the CTPs of the municipality of Balancán, Tabasco, and in certain places with similar biophysical characteristics to those of the study area, since they may be used as a reference point in the forest management of the plantations.
According to Frangi et al. (2016) and Santiago et al. (2015), Eucalyptus grandis has a rapid growth; for this reason, the forest shifts are short compared to those of other species destined for sawmilling. The following is a brief comparison and a description of the relationship between the five shifts considered.
A growing relationship was observed in the shift rotation with the incorporation of environmental and economic variables such as the carbon capture. In general terms, the rotation has diminished as a larger number of economic aspects (costs) are considered in its determination; conversely, it has increased with the inclusion of environmental and recreational aspects (income). The corresponding behavior was as follows: Maximum Average Production (10.24 years), Faustmann shift (10.82 years), Hotelling shift (11.32 years), Hartman shift (11.64) and Maximum Total Production (97.20 years).
In the analysis of shifts, the Hartman shift was observed to increase by 3.2 months compared to the Hotelling shift; in relation to the Faustmann shift, the increase was 9.8 months, and with regard to the MAP, it was 16.8 months.
Similar data were estimated in the state of Oaxaca for this species (Téllez et al., 2008), after analyzing two scenarios -1) wood for cellulose and 2) wood for sawmilling and pulp- with an economic approach. In the first scenario, the shift was determined to range between 6.9 and 9.0 years, while for the second, it ranges between 9.0 and 13.5 years; when an income for carbon capture was incorporated into the calculation, the shift increased between 12 and 20, and 17 and 30 months, respectively. Certain authors consider that the forest shifts of Eucalyptus grandis in Colombia range between 6 and 8 years (Restrepo and Alviar, 2010; Gómez et al., 2012).
It is worth mentioning that the extension of the forest shift is a consequence of the genesis (structure) of each model, and that it favors the generation of (larger quantities of) heartwood and the capture of carbon. Dias et al. (2016) points out that for the genus Eucalytus short shifts result in good growth rates but a poor quality as wood, as pulp for the manufacture of paper, and for the drying process. Therefore, an extension of the shift makes it possible to obtain timber with better anatomical features.
Conclusions
As economic-environmental aspects are incorporated into the estimation of the forest shifts for Eucalyptus grandis, the optimal felling age increases.
The estimation of forest shifts for E. grandis is shown to involve a maximum average production, a Faustmann shift, a Hotelling shift, a Hartman shift and a maximum total production.
The Hartman shift is suitable for sustainable forest harvesting, inasmuch as it incorporates aspects of the proposal of Faustmann as well as the value of the environmental and recreational services provided by the plantation.
The extension of the forest shifts increases the volume of biomass, with the possibility of harvesting larger quantities of heartwood for cellulose and capturing more carbon, whereby the social benefit is enhanced.
Acknowledgments
The authors wish to express their gratitude to Conacyt for the funds provided for the conduction of this research.
REFERENCES
Álvarez L., P. S., A. Perales S. y E. Trujillo U. 2015. El subsector forestal mexicano y su apertura comercial. Revista Mexicana de Ciencias Forestales 6 (29): 8-23. [ Links ]
Andreoni, M. I. y A. Bussoni. 2014. Evaluación económica de dos programas de mejoramiento genético en Eucalyptus grandis. Agrociencia Uruguay. 18 (1): 153-162. [ Links ]
Barton B., D. y L. Merino P. 2004. La experiencia de las comunidades forestales en México: Veinticinco años de silvicultura y construcción de empresas forestales comunitarias. Instituto Nacional de Ecología. México, D. F., México. 269 p. [ Links ]
Bonilla G., J. A. y J. A. Alarcón N. 2015. Turnos técnico y económico de la tala para arboles de Romerillo Blanco en Ecuador. Ecología Aplicada 14 (2):127-137. [ Links ]
Chang, S. J. 1998. A generalized Faustmann model for the determination of optimal harvest age. Canadian Journal of Forest Research 28 (5): 652-659. [ Links ]
Comisión Nacional Forestal (Conafor). 2016. Plantaciones Forestales Comerciales. Jalisco, México. http://www.conafor.gob.mx/web/temas-forestales/plantaciones-forestales/ (20 de agosto 2015). [ Links ]
Dias S., B. C., J. Tarcísio L. and J. R. Moreira D. 2016. Analysing the drying behavior of juvenile and mature Eucalyptus saligna wood in drastic drying test for optimal drying schedule. Maderas, Ciencia y Tecnología 18(4): 543-554. [ Links ]
Díaz, B., L. 1997. Turno forestal económicamente óptimo: Una revisión. Revista Española de Economía Agraria 180: 181-224. [ Links ]
Frangi, J., C. Pérez, J. Goya, N. Tesón, M. Barrera y M. Arturi. 2016. Modelo empírico integral de una plantación de Eucalipto grandis en Concordia, Entre Ríos. Bosque (Valdivia). 37 (1): 191-204. [ Links ]
Geréz F., P. y M. del R. Pineda L. 2011. Los bosques de Veracruz en el contexto de una estrategia estatal REDD+. Madera y Bosques 17 (3): 7-27. [ Links ]
Gómez, E. A., L. A. Ríos y J. D. Peña. 2012. Madera, un Potencial Material Lignocelulósico para la Producción de Biocombustibles en Colombia. Información Tecnológica 23 (6): 73-86. [ Links ]
Hoen, H. F. and B. Solberg. 1994. Potential and economic efficiency of carbon sequestration in forest biomass through silvicultural management. Forest Science 40 (3): 429-451. [ Links ]
López H., J. A. y A. G. Valles G. 2009. Modelos para la estimación del índice de sitio para Pinus durangensis Martínez en San Dimas, Durango. Ciencia forestal en México 34 (105): 185-196. [ Links ]
Luján A. C., J. M. Olivas G., H. G. González H., S. Vázquez A., J. C. Hernández D. y H. Luján A. 2016. Desarrollo forestal comunitario sustentable en la región norte de México y su desafío en el contexto de la globalización. Madera y Bosques 22 (1): 37-51. [ Links ]
Medema, E. L. and G. W Lyon. 1985. The determination of financial rotation ages for coppicing tree species. Forest Science 31 (2): 398-404. [ Links ]
Montgomery, D. C., E. A. Peck. y G. G. Vining. 2007. Introducción al análisis de regresión lineal. (3a ed.). Ed. Grupo patria cultural. México, D. F., México. 587 p. [ Links ]
Municipios.mx. 2016. Todos los municipios de México. http://www.municipios.mx/tabasco/balancan/ (20 de agosto de 2016). [ Links ]
Restrepo, C. y M. Alviar. 2010. Tasa de descuento y rotación forestal: el caso del Eucalyptus saligna. Lecturas de Economía (73): 149-164. [ Links ]
Romero, C. 2001. Economía de los recursos ambientales y naturales. 2a ed. Alianza editorial. Madrid, España. 216 p. [ Links ]
Romero, C., V. Ros and L. Díaz B. 1998. Optimal forest rotation age when carbon captured is considered: theory and applications. Journal of the Operational Research Society 49 (2): 121-131. [ Links ]
Santiago S., D. G., E. Valadez M. y D. Cibrián T. 2015. Identificación molecular del complejo Botryosphaeria sp. asociado a cancros y secamiento de yemas en Eucalyptus sp. Revista Mexicana de Ciencias Forestales 6 (32): 93-106. [ Links ]
Secretaría de Medio ambiente y Recursos Naturales (Semarnat). 2010. Anuario Estadístico de la Producción Forestal 2010, Subsecretaria de Recursos Naturales. http://www.gob.mx/cms/uploads/attachment/file/43385/ANUARIO_2010.pdf (20 de agosto de 2016). [ Links ]
Secretaría de Medio ambiente y Recursos Naturales (Semarnat). 2014. Anuario Estadístico de la Producción Forestal 2011, Subsecretaria de Recursos Naturales. Dirección General Forestal. http://www.gob.mx/cms/uploads/attachment/file/43388/ANUARIO_2011.pdf (20 de agosto de 2016). [ Links ]
Smart, J. C. R. and J. C. Burgess. 2000. An environmental economic analysis of willow SRC production. Journal of Forest Economics 6 (3):193-225. [ Links ]
Smith, T. M., W. P. Cramer, R. K. Dixon, R. Leemans, R. P. Neilson and A. M. Solomon. 1993. The global terrestrial carbon cycle. Water, Air, and Soil Pollution 70(1-4): 19-37. [ Links ]
Stainback, G. A. and J. R. R. Alavalapati. (2002). Economic analysis of slash pine forest carbon sequestration in the southern US. Journal of Forest Economics 8(2): 105-117. [ Links ]
Tait, D. E. 1986. A dynamic programming solution of financial rotation ages for coppicing tree species. Canadian Journal of Forest Research 16 (4): 799-801. [ Links ]
Téllez, M. E., M. D. J. González G., H. M. De los Santos P., A. M. Fierros G., R. J. Lilieholm and A. Gómez G. 2008. Rotación optima en plantaciones de eucalipto al incluir ingresos por captura de carbono en Oaxaca, México. Revista Fitotecnia Mexicana 31 (2): 173-182. [ Links ]
Van, K. G. C., C. S. Binkley and G. Delcourt. 1995. Effect of carbon taxes and subsidies on optimal forest rotation age and supply of carbon services. American Journal of Agricultural Economics 77 (2): 365-374. [ Links ]
Received: December 13, 2017; Accepted: April 30, 2018











 texto em
texto em