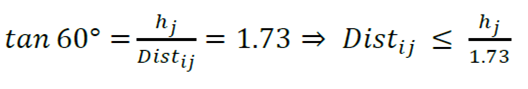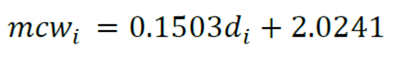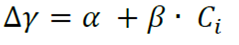Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias forestales
versión impresa ISSN 2007-1132
Rev. mex. de cienc. forestales vol.9 no.45 México ene./feb. 2018
https://doi.org/10.29298/rmcf.v9i45.145
Articles
Influence of competition on the diametric growth of Pinus durangensis Martínez in Durango, Mexico
1Facultad de Ciencias Forestales, Universidad Autónoma de Nuevo León. México.
2Instituto de Silvicultura e Industria de la Madera, Universidad Juárez del Estado de Durango. México.
3Instituto Tecnológico de El Salto. México.
4CERNA Ingeniería y Asesoría Medioambiental S.L.P. España.
In this paper the effect of competition on individual tree diameter growth of Pinus durangensis was analyzed. Trees were growing in mixed and uneven-aged stands in Durango, Mexico. The data used in the study were obtained from two forest inventories performed in 2009 and 2014 in 16 permanent sampling plots for forest and soil research (SPIFyS) of 2 500 m2 in size. Pinus durangensis was the dominant species within the sites, covering 39.44 % of the importance value, and it is growing with other 18 tree species. 14 distance-independent and 11 distance-dependent competition indices were used to evaluate the effect of competition. 11 competitor selection methods were tested in combination with the selected distance-dependent indices. Distance-independent competition indices showed slightly better results than distance-dependent indices for predicting diameter at breast height growth for the studied tree species. The distance-independent competition index derived from the ratio between of the basal area of the reference tree and the basal area per hectare best described the effect of the competition, and therefore, it is recommended for its possible addition within further models to predict the breast height diameter growth for the tree species analyzed in this study.
Key words: Diameter growth; competitor selection method; exponential equation; linear equation; power equation; distance-independent and distance-dependent competition index
En esta investigación se analizó la influencia de la competencia sobre el crecimiento en diámetro normal en árboles de Pinus durangensis en bosques mixtos e irregulares del estado de Durango. Se utilizaron datos de dos inventarios realizados en 2009 y 2014, en 16 Sitios Permanentes de Investigación Forestal y de Suelos (SPIFyS) de 2 500 m2, dentro de los cuales, Pinus durangensis fue la especie dominante del estrato arbóreo, con 39.44 % del valor de importancia, y crece de manera mezclada con otras 18 especies arbóreas. El efecto de la competencia fue analizado mediante 14 índices de competencia independientes de la distancia y 11 dependientes de la distancia; para ello, se evaluaron 11 criterios de selección de árboles competidores. Los índices independientes de la distancia explicaron ligeramente mejor que los índices dependientes de la distancia el crecimiento en diámetro normal de la especie estudiada. El índice de competencia independiente de la distancia que se deriva de la razón entre el área basal del árbol objetivo y el área basal por hectárea describió mejor el efecto deseado, por lo que se recomienda para su posible inclusión en futuros modelos de crecimiento en diámetro normal desarrollados para P. durangensis.
Palabras Clave: Crecimiento en diámetro; criterio de selección de competidores; ecuación exponencial; ecuación lineal; ecuación de potencia; índices de competencia dependiente e independiente de la distancia
Introduction
In forest ecology, competition can be defined as the negative effect that a tree exerts on another due to consumption or control over the access to a specific resource (light, water or nutrients) of limited availability (Burkhart and Tomé, 2012). The effect of this force can lead to a reduction in the survival, growth or reproduction of the affected individual, as it is one of the fundamental factors in the evolution and functioning of ecosystems (Pretzsch, 2009).
Competition has been studied through the use of indices by a large number of researchers for more than half a century (Clark and Evans, 1954; Arney, 1973, Alemdag, 1978; Lorimer, 1983; Tomé and Burkhart, 1989; Biging and Dobbertin, 1995; Corral et al., 2005). An index of this type is an indicator that estimates the total competition to which a tree is subjected and that manifests itself in its growth (Burkhart and Tomé, 2012).
Munro (1974) classifies these indices into two groups: distance-independent, which do not consider the spatial distribution of the trees and do not require obtaining the coordinates of it, and distance-dependent indices, which do include the spatial distribution with respect to the target tree.
According to Biging and Dobbertin (1995), Bachmann (1998) and Corral et al. (2005), the impact of the competition exerted by one or more individuals on the growth of a tree can be approached with similar results through the use of independent or distance-dependent indices, using for the latter an adequate method for the selection of the competing trees of a target tree. This aspect is one of the indispensable factors for the construction of an individual tree growth model, especially if it is a species in mixed and irregular forests (Schröder and Gadow, 1999). However, these studies have been carried out mainly in plantations of only one species, so those related to irregular forests and with more than one species are still very scarce (Moravie et al., 1999; Coates et al., 2009; Seydack et al., 2011).
Thus, the following targets were proposed: a) to estimate the significance of the effect of competition on the growth in normal diameter of Pinus durangensis Martínez trees in mixed and irregular stands in the state of Durango; b) compare the ability to describe the competence of independent and distance-dependent indices with different criteria for the selection of competitors, and c) identify the best competitive index or the best combination of a competitive index with a selection criteria of competitors to be incorporated in a future growth model in normal diameter of this species.
Materials and Methods
Study area
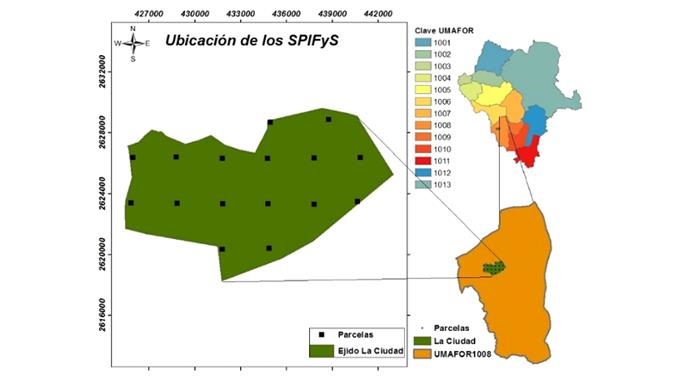
The data come from 16 Permanent Forest and Soil Research Sites (SPIFyS) established in the La Ciudad ejido, Pueblo Nuevo municipality, Durango, which is located within the Regional Forest Management Unit (UMAFOR) 1008. Forest communities most important of the UMAFOR 1008 are composed of forests mixed with species of Pinus and Quercus, Juniperus, Arbutus and Alnus; they are stands of second growth that have been subject to forest exploitation for more than 100 years (Luján et al., 2015). The size of the plots was 50 × 50 m (0.25 ha), and they were systematically located within the boundaries of the ejido (Figure 1).
Data collection
The data were taken in two dates; the first one when the SPIFyS were installed and the original inventory was made in 2009, and the second one when the second inventory was made in 2014, five years after; in such a period, the sites were not subjected to any forestry treatment.
For each measurable tree (normal diameter ≥ 7.5 cm) within each site, the following variables were taken: species, dominance, normal diameter (d, cm), with a using a Haglöf Mantax Blue caliper with millimeter graduation and following the directions of the sides of the plot; total height (h, m), clean stem height (m), distance from the tree to the center of the site (m) and crown diameter (m), with a Vertex IV graded hypsometer (cm), and the azimuth of the tree with respect to the center of the site, with a Suunto Tandem Global Compass / Clinometer instrument.
Pinus durangensis Martínez was the dominant species within the study area since it records 39.44 % of importance value (Campo and Duval, 2014), but it is mixed with the following species, which follow a decreasing sequence according to their importance value (numbers in parentheses): Pinus cooperi Blanco (11.51 %), Quercus sideroxyla Bonpl. (7.14 %), Juniperus deppeana Steud. (5.92 %), Alnus firmifolia Fernald (3.47 %), P. strobiformis Engelm. (3.42 %), Q. crassifolia Humb. et Bonpl. (3.23 %), P. leiophylla Schiede ex Schltdl. & Cham. (3.03 %), Q. rugosa Neé (2.92 %), Arbutus arizonica (A. Gray) Sarg (2.64 %), P. herrerae Martínez (2.32 %) A. madrensis M. González (2.23 %), A. bicolor S. González, M. González et P. D. Sørensen (2.08 %), P. teocote Schltdl. & Cham. (1.96 %), A. tessellata P. D. Sørensen (1.80%), A. xalapensis Kunth (1.72 %), Q. conzattii Trel. (1.65 %), Q. durifolia Seemen (1.69 %) and Populus tremuloides Michx. (1.60 %). In Table 1 are shown the descriptive statistics of the mensuration variables of the two inventories carried out in the SPIFyS until now.
Table 1 Main mensuration variables of the Permanent Sites for Forest and Soil Investigation in the actual study.
| Variable | Mean ± SD (2009) | Mean± SD (2014= |
|---|---|---|
| N | 666 ± 354 | 612 ± 326 |
| G | 23.09 ± 7.77 | 26.55 ± 8.58 |
| Dg | 23.78 ± 6.67 | 25.83 ± 6.57 |
| V | 224.11 ± 83.17 | 274.03 ± 103.79 |
| H0 | 20.14 ± 3.9 | 21.69 ± 4.07 |
N = Number of trees per ha; G = Basimetric area inn m2 per ha; Dg = Squared mean diameter in cm; V = Volume per ha in m3; H0 = Dominant height in m.
Analyzed competition indexes
In tables 2 and 3 are shown the competition indexes that were analyzed: 14 of them belong to the distance-independence group (IC 1 - IC 14 ), and 11 to the distance-dependent (ICd 1 - ICd 11 ) (Munro, 1974), which were selected from previous experiences (Martínez and Madrigal, 1982; Pukkala and Kolström, 1987; Holmes and Reed, 1991; Biging and Dobbertin, 1992; Mäkinen, 1997; Schröder and Gadow, 1999; Álvarez et al., 2003; Corral et al., 2005; Crecente et al., 2007).
Table 2 Mathematical expression of the distance-independent competition indexes used in this study.

n = Number of trees per site; S = Surface area of the site (m2); 𝑑 𝑖 = Normal diameter of the target tree (cm); log = Logarithm base 10; 𝑑 𝑔 = Quadratic diameter (cm); 𝑑𝑐 𝑖 = Crown diameter in horizontal projection of the target tree (m); 𝑑𝑐𝑚 𝑖 = Maximum crown diameter (in free growth) of the target tree (m) estimated by equation (3); 𝑑𝑐𝑚 𝑚𝑎𝑦𝑜𝑟 𝑖 = Crown diameter in horizontal projection of the larger trees than the target tree (m); 𝑑 𝑚𝑎𝑦𝑜𝑟 𝑖 = Normal diameter of the larger trees than the target tree (cm); 𝑔 𝑖 = Normal section of the target tree (m2) ; G= Basimetric area (m2 ha-1); BAL = BAL index; IH = Hart index.
Table 3 Mathematical expression of the distance- dependent competition indexes used in this study.

L ij =Length (m) of the segment that links the center of the target tree and its competitor, included the overlay area of its influence zones; 𝑂 𝑖𝑗 = Overlay area (m2) between the influence zones of the target tree and the competitor tree; 𝑍 𝑖 = Influence zone of the target tree (m2); 𝑑 𝑗 = Normal diameter of the competitor tree (cm); 𝐷𝑖𝑠𝑡 𝑖𝑗 = Distance in horizontal projection between the target tree and the competitor tree (m); nc = Number of competitor trees ; ℎ 𝑖 = Total target tree height (m); ℎ 𝑗 = Total competitor tree height (m); 𝐶𝐶 𝑖 = Crown surface in horizontal projection of the target tree (m2) at a certain p percentage of its height; 𝐶𝐶 𝑗 = Crown surface in horizontal projection of the competitor tree (m2) at a certain p percentage of its height; 𝐶𝑉 𝑖 = Crown volume of the target tree (m3 over a certain p percentage of its height; 𝐶𝑉 𝑗 = Crown volume of the competitor tree (m3) over a certain p percentage of its height; 𝐶𝑉 ∝𝑗 = Crown volume of the competitor 𝑗 tree over the ∝ point.
Selection criterion for the competitors
Eleven Pinus durangensis competitor tree selection criteria were analyzed (C 1 to C 11 codes). Through this C 1 criterion, all of the individuals included in this moving Bitterlich plot with center in the target tree and a basimetric area factor (BAF) equal to 4 m2 ha-1 were selected as the competitor trees of this species. According to this criterion, in order to consider a tree as a competitor of the target tree, the distance between them cannot be higher than 25 times its own normal diameter (Crecente et al., 2007).
In criterion C 2 , all those selected with criterion C 1 were considered to be competing trees, as well as the closest tree that is located within each of the quadrants defined by the four cardinal points (Crecente et al., 2007). With criterion C 3 , the four trees closest to the target tree were selected (Crecente et al., 2007). Criterion C 4 , proposed by Biging and Dobbertin (1992), was based on considering active competitors those trees whose total height ( ℎ 𝑗 ) exceeds an imaginary line drawn from the base of the objective tree with an inclination of 60º with respect to the horizontal (Figure 2). This line marks a point (at its intersection with the axis of the competitor tree) from which the volume of the cup was considered to calculate the ICd 11 competition index. The relationship between distance and height that determined whether a tree was selected as an active competitor was:
Where:
h j = Total height of the competing tree (m)
Dist ij = Distance from the target tree to the competing tree (m)
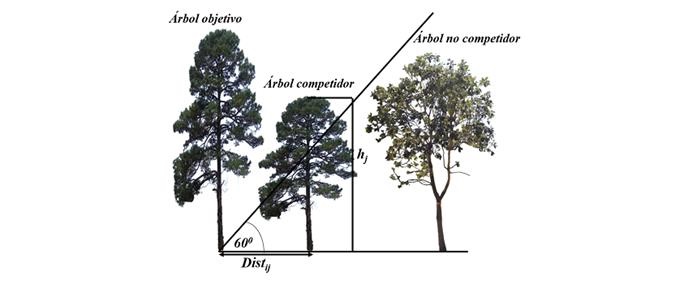
Árbol objetivo = Target tree; Árbol competidor = Competitor tree; Árbol no competidor = No competitor tree
Figure 2 Scheme of C 4 competitor selection criterion.
The C5 criterion differs from the former in that the inclined line originates at the basis of the target tree crown (Figure 3). The relation between the distance and height that determines if a tree is selected as an active competitor was:
Where:
h j = Total height of the competing tree (m)
Dist ij = Distance from the target tree to the competing tree (m)
HBC i = Height at the crown base of the target tree (m)
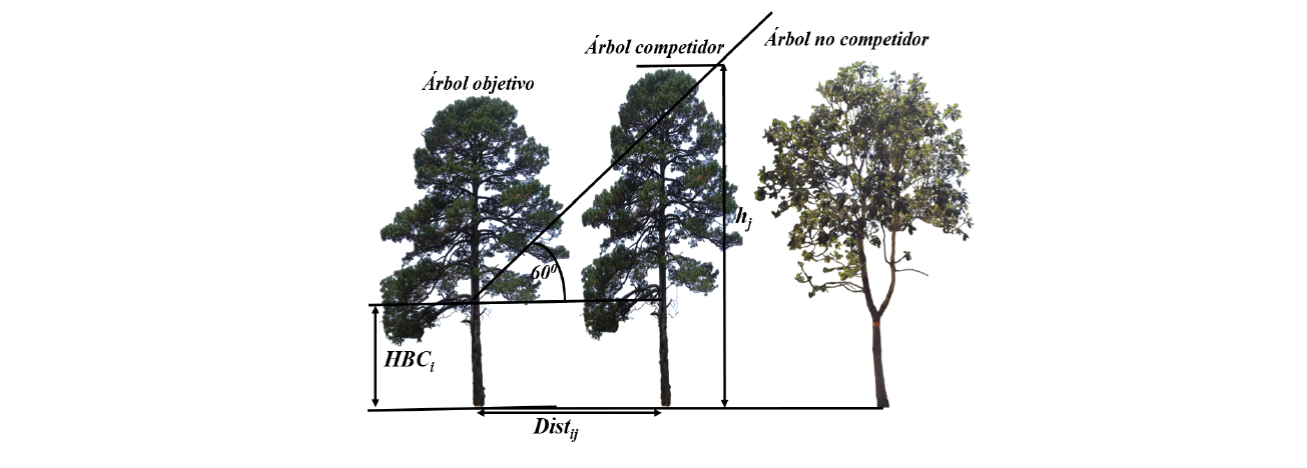
Árbol objetivo = Target tree; Árbol competidor = Competitor tree; Árbol no competidor = No competitor tree
Figure 3 Scheme of C 5 competitor selection criterion.
Criterion C 6 was based on the concept of the area of influence (Staebler, 1951). For this case, all the trees whose area of influence overlapped that of the target tree were considered active competitors (Figure 4). In this work, the maximum value that was taken was the radius of the tree crown it could reach if it were growing free of competition, which was estimated by the equation proposed by Cruz and Castañeda (1999):
Where:
mcw i = Maximum crown growth (m)
d i = Normal diameter (cm) of the selected tree

Árbol objetivo = Target tree; Árbol competidor = Competitor tree; Árbol no competidor = No competitor tree
Figure 4 Scheme of C 6 competitor selection criterion.
The criterion C 6 is the only one that may be used with the competition indexes based upon the concept of the zone of influence (ICd 1 , ICd 2 and ICd 3 ).
The criteria C 7 to C 11 include the concept of angle for the elimination of competition (Lee and Gadow, 1997), according to which it is chosen as the first active competitor the closest tree to the target tree; afterwards, a circular section is marked with a particular angle and whose bisectrix is the line that joins both of them. All the trees in this circle that stand behind the first competitor, are discarded as possible active competitors. The process continues with the selection of the next closer tree to the target and located outside of the first circle, and it goes on and oh until all the active competitors are found (Figure 5), with a 60° elimination angle (C 9 ).
The number of active competitors decreases as the elimination angle of competition increases. In other investigations, they have used competition elimination angles of 90, 75, 60, 45 and 30 degrees, which define criteria C 7 to C11, respectively (Corral et al., 2005; Crecente et al., 2007).
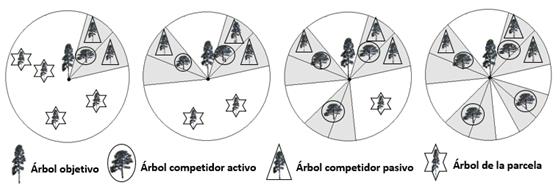
Árbol objetivo = Target tree; Árbol competidor activo = Active competitor tree; Árbol competidor pasivo = Passive competitor tree; Árbol de la parcela = Plot tree.
Figure 5 Scheme of the process to select active competing trees from a reference tree, taking into account an elimination 60° angle (criterion C 9 ).
Analyzed models
Three models were used, one of simple lineal type, one exponential and another potential (equations 4 to 6) to analyze the influence that competition exerts on the growth in normal diameter of Pinus durangensis trees within the studied sites. The models were tested for all possible combinations between the indexes and the criteria for selecting competitors:
Where:
Δ = Variable to be modeled (normal diameter growth during a 5 year period)
= Variable to be modeled (normal diameter growth during a 5 year period)
C i = Distance-independent index of competition or the combination of a distance-dependent competition index with a criterion of competitors’ selection
α y β = Parameters to be estimated in the model fit
The estimation of the parameters of the linear model was performed by least squares using the REG procedure of the SAS / STAT® program (SAS, 2004). In the case of non-linear models, the NLIN procedure implemented in the same program was used.
The goodness of fit of the models (i.e. significance of the effect of competition on the growth in normal diameter) was evaluated through the significance of the adjustments of the models and with the statistical coefficient of determination (R2) and root mean square error (REMC). For the exponential and potential models, the estimated coefficient of determination corresponded to that proposed by Ryan (1997) for non-linear regression, which is equivalent to the square of the correlation coefficient of the observed values and the values estimated by the models.
Results and Discussion
Table 4 lists the ten competition or combinations of competition index with a criterion of selection of competitors that showed the greatest levels of explanation of the observed variability in normal diameter growth of Pinus durangensis trees, taking as predictive variable the competition in the three studied models. These indexes also recorded the least mean errors, and in all cases, fit was very significant (p<0.0001), which means that the use of competition as a predictive variable vigorously helps to explain growth in normal diameter of the studied species.
Table 4 Competition indexes which showed the best statistics of fit of diameter growth models of linear, exponential and potential type.
| Lineal | Exponential | Potential | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cr | IC | R 2 | REMC | Cr | IC | R 2 | REMC | Cr | IC | R 2 | REMC |
| IC 6 | 0.33 | 0.76 | C11 | ICd 4 | 0.29 | 0.78 | IC 12 | 0.35 | 0.74 | ||
| IC 8 | 0.28 | 0.79 | C10 | ICd 4 | 0.28 | 0.78 | C11 | ICd 4 | 0.28 | 0.78 | |
| IC 10 | 0.27 | 0.79 | C2 | ICd 4 | 0.28 | 0.78 | C10 | ICd 4 | 0.28 | 0.78 | |
| IC 11 | 0.26 | 0.79 | C9 | ICd 4 | 0.27 | 0.79 | IC 11 | 0.27 | 0.79 | ||
| IC 12 | 0.25 | 0.80 | IC 10 | 0.26 | 0.79 | C3 | ICd 4 | 0.27 | 0.79 | ||
| IC 9 | 0.23 | 0.81 | C8 | ICd 4 | 0.26 | 0.79 | C9 | ICd 4 | 0.27 | 0.79 | |
| C11 | ICd 5 | 0.22 | 0.82 | C7 | ICd 4 | 0.25 | 0.80 | C3 | ICd 5 | 0.26 | 0.79 |
| C7 | ICd 5 | 0.21 | 0.82 | C3 | ICd 4 | 0.25 | 0.80 | C2 | ICd 4 | 0.26 | 0.79 |
| C3 | ICd 5 | 0.20 | 0.82 | IC 11 | 0.22 | 0.81 | C7 | ICd 4 | 0.25 | 0.80 | |
| C10 | ICd 5 | 0.20 | 0.83 | IC 9 | 0.22 | 0.82 | C8 | ICd 4 | 0.25 | 0.80 | |
Cr = Competitor selection criteria; IC = Competence index; R2 = Coefficient of determination; REMC = Root of the mean square error.
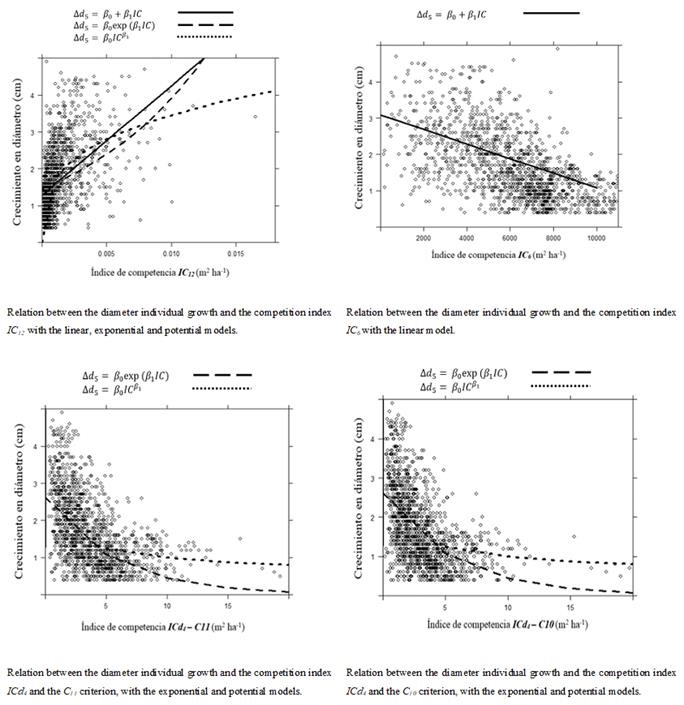
The best values of the statistics of fit R2 and REMC were obtained with the independent indexes of the distance and the use of the potential and linear models. The IC 12 index (which is based on the calculation of the ratio of the basal area of the target tree and the basal area per hectare), was the one that presented the best fit by using the potential model, explaining 35 % of the variability observed in the growth in diameter of the species studied, with a CTM value of 0.74 cm; followed by the IC 6 that represents the crown competition factor (CCF), defined as the percentage of the growth area occupied by the projection of the crowns, assuming that each tree grows freely (without competition), explaining through the linear model, 33 % of the variability observed in the growth in diameter during the observation period, with a CTMR of 0.76 cm.
The independent- distance indexes IC 8 and IC 10 also showed good results in the explanation of the variance observed in the growth in diameter. The results of this work are consistent with those by Crecente et al. (2007) in plantations of Pinus radiata D. Don in Galicia, Spain, where the independent indexes of distance presented slightly better results than those distance -dependent in the study of the effect of competition.
Valles and Valadez (2006) also found better fits with the use of a distance-independent competition index based on the density-weighted canopy width in mixed forests in San Dimas, Durango. In the same way, Tíscar and Tíscar (2010) reported in a population of Pinus nigra Arnold from the Sierra de Cazorla (southeast of Spain), a distance -independent index that includes the variable crown area as the most suitable to be included in models for the prediction of growth in normal diameter. However, the R2 values of this work are lower to those of Álvarez et al. (2004), who reported values of 0.66 for the distance -independent indexes of the BAL and BALMOD, in an exponential model fitted in growth data in section of individual trees of Pinus radiata in El Bierzo (León, Spain).
Other researchers such as Álvarez et al. (2003), Biging and Dobbertin (1995), Corral et al. (2005) and Schröder and Gadow (1999) reported that independent- distance indexes based on the use of the basal area (BAL and BALMOD) produced significant improvements in the estimates of diameter growth models of species studied in even-aged stands.
On the other hand, the indexes based on stand density (number of trees per hectare, basal area per hectare, Reineke, crown competition factor, and Hart index) were not adequate to evaluate the effect of competition, since they did not explain even 15 % variation in the growth data, so its use is not recommended as competition indices. These results are common with previous studies conducted on Quercus robur L. (Maseda, 1998) and on Pinus radiata (Álvarez, 1998, Álvarez et al., 2003).
Within the group of distance- dependent competition indexes, the ICd 4 combined with C 10 and C 11 had the best results with the exponential model, as it explained 29 % of the variability observed in diameter growth with REMC values of 0.78 cm. This competitor selection criteria (C 10 and C 11 ) use 45° y 30° angles for competing elimination and are rather simple to apply since they limit the number of competitors, which might make them useful in field work (Álvarez et al., 2003).
ICd 5 stands in second place, which also provided good results when combined with criterion C 3 . These indices are strongly related to each other, since they are based on ratios of sizes (normal diameter) weighted by distances, and consider that the competition that exerts on a tree around them increases when their size increases and the distance that separates them (Crecente et al., 2007).
Figure 6 shows the relation between the distance independent competition indexes IC 6 and IC 12 and the distance dependent index ICd 4 with the C 11 and C 10 criteria with individual diametric growth of Pinus durangensis by the linear, exponential and potential models, or just with the one of the best fit. In most cases, the potential model best describes the tendency of the data when using the competition indexes as predictive variable, a situation that explains itself as values under the squared mean error are obtained, compared to the linear and exponential equations.
In general, the value of the different selection criteria for the selection of competitors for a same index, does not exhibit great contrasts, and even though there is always one that is slightly more favorable, the others have a value rather close to it.
Although the results suggest that the best independent distance indexes of distance IC 6 and IC 12 explain between 33 and 35 % of the variance observed in diameter growth, it is evident that when developing the growth model it would be necessary to include others as predictive variables, such as the initial normal diameter, the quality of the season, and other factors that significantly influence the increase in the normal section of trees (López et al., 2013; Quiñonez et al., 2015).
Conclusions
The fit of most of the tested models resulted significant, which means that the use of competition as a predictive model helps vigorously to explain growth of Pinus durangensis normal diameter. The distance independent indexes resulted as better predictive variables than the distance dependent to assess the influence of competition of Pinus durangensis that grows in mixed and irregular forests in Durango state. The IC 12 index which came from the ratio between the basimetric area of the target tree and the basimetric area per hectare better described the effect of competition; therefore, it is advised to include it in future growth models of normal diameter for the studied species. Its application in the model is an easy task, since during the inventories for forest management that are performed in the study area every 10 years, the necessary variables for the calculation of this index are taken.
Acknowledgements
Thanks to Conacyt for the financial support granted to the first author to study the Doctoral program of the Facultad de Ciencias Forestales of the Universidad Autónoma de Nuevo León.
REFERENCES
Alemdag, I. S. 1978. Evaluation of some competition indices for the prediction of diameter increment in planted White spruce. Canadian Forestry Service, Department of the Environment. Forest Management Institute Information Report FMR-X-108. Ottawa, Ontario, Canada. 39 p. [ Links ]
Álvarez T., M. F. 1998. Influencia de la competencia en el crecimiento en sección en Pinus radiata D.Don. Proyecto fin de carrera. EPS. Lugo. Universidad de Santiago de Compostela. Santiago de Compostela, Galicia, España. pp. 1-45. [ Links ]
Álvarez T., M. F., M. Barrio, J. Gorgoso y J. G. Álvarez. 2003. Influencia de la competencia en el crecimiento en sección en Pinus radiata D. Don. Investigación Agraria. Sistemas y Recursos Forestales 12(2): 25-35. [ Links ]
Álvarez T., M. F., R. A. Marqués G., M. Fernández y F. Castedo V. 2004. Influencia de la competencia en el crecimiento en sección de Pinus radiata D. Don en el Bierzo (León). Cuadernos de la Sociedad Española de Ciencias Forestales 18: 129-133. [ Links ]
Arney, J. D. 1973. Tables for quantifying competitive tress on individual trees on individual trees. Canadian Forestry Service. Information Report BCX-78. Victoria, British Columbia, Canada. 45 p. [ Links ]
Bachmann, M. 1998. Indizes zur Erfassung der Konkurrenz von Einzelbäumen. Methodische Untersuchung in Bergmischwäldern. Forstliche Forschungsberichte München Nr. 171. München, Bayern, Deutschland. 171 p. [ Links ]
Bella, I. E. 1971. A new competition model for individual trees. Forest Science 17(1): 364-372. [ Links ]
Biging, G. S. and M. Dobbertin. 1992. A comparison of distance-dependent competition measures for height and basal area growth of individual conifer tress. Forest Science 38(3): 695-720. [ Links ]
Biging, G. S. and M. Dobbertin. 1995. Evaluation of competition indices in individual tree growth models. Forest Science 41(2): 360-377. [ Links ]
Braathe, P. 1980. Height increment of young single trees in relation to height and distance of neighbouring trees. Mitteilungen der Forstlichen Bundesversuchsanstalt 130: 43-47. [ Links ]
Burkhart, H. E. and M. Tomé. 2012. Modeling Forest Trees and Stands. Springer. Dordrecht, Netherlands. 458 p. [ Links ]
Campo, A. M. y V. S. Duval. 2014. Diversidad y valor de importancia para la conservación de la vegetación natural. Parque Nacional Lihué Calel (Argentina). Anales de Geografía 34(2): 25-42. [ Links ]
Clark, P. J. and F. C. Evans. 1954. Distance to nearest neighbor as a measure of spatial relationships in population. Ecology 35: 445-453. [ Links ]
Coates, K. D., C. D. Canham and P. T. LePage. 2009. Above- versus below-ground competitive effects and responses of a guild of temperate tree species. Journal of Ecology 97: 118-130. [ Links ]
Corral R., J. J., J. G. Álvarez, O. Aguirre and F. J. Hernández. 2005. The effect of competition on individual tree basal area growth in mature stands of Pinus cooperi Blanco in Durango (Mexico). European Journal of Forest Research 124: 133-142. [ Links ]
Crecente C., F., E. Vázquez-Gómez, R. Rodríguez-Soalleiro y U. Diéguez-Aranda. 2007. Influencia de la competencia en el crecimiento individual de Pinus radiata D. Don en Galicia. Cuadernos de la Sociedad Española de Ciencias Forestales 23: 167-174. [ Links ]
Cruz, C. F. y A. J. Castañeda. 1999. Guía de densidad para Pinus cooperi var. blanco del “Ejido La Victoria” Pueblo Nuevo Durango. In: X Congreso de la Dirección General de Educación Tecnológica Agropecuaria. 24 al 26 de noviembre. Oaxaca, Oax., México. 5 p. [ Links ]
Daniels, R. F., H. E. Burkhart and T. R. Clason. 1986. A comparison of competition measures for predicting growth of loblolly pine trees. Canadian Journal of Forest Research 16(6): 1230-1237. [ Links ]
Gerrard, D. I. 1969. Competition quotient: a new measure for the competition affecting individual forest trees. Michigan State University. Agriculture Research Station. Research Bulletin 20. Lansing, MI, USA. 32 p. [ Links ]
Hegyi, F. 1974. A simulation model for managing jack pine stands. In: Fries, J. (ed.). Growth models for tree and stand simulation. Royal College of Forestry, Department of Forest Yield Research. Research Note Num. 30. Stockholm, Sweden. pp. 74-90. [ Links ]
Holmes, M. J. and D. D. Reed . 1991. Competition indices for mixed species northern hardwoods. Forest Science 37(5): 1338-1349. [ Links ]
Krajicek, J. E., K. A. Brinkman and S. F. Gingrich. 1961. Crown competition: a measure of density. Forest Science 7(1): 35-42. [ Links ]
Lee, D. T. and K. von Gadow. 1997. Iterative Bestimmung der Konkurrenzbäume in Pinus densiflora Beständen. Allgemeine Forst- und Jagdzeitung 168(3-4): 41-44. [ Links ]
López, L., R. Villalba and F. Bravo. 2013. Cumulative diameter growth and biological rotation age for seven tree species in the Cerrado biogeographical province of Bolivia. Forest Ecology and Management 292: 49-55. [ Links ]
Lorimer, C. G. 1983. Test of age-independent competition indices for individual tree in natural hardwood stands. Forest Ecology and Management 6(4): 343-360. [ Links ]
Luján S., J. E., J. J. Corral R., O. A. Aguirre C. and K. von Gadow. 2015. Grouping forest tree species on the Sierra Madre Occidental, Mexico. Allgemeine Forst- und Jagdzeitung 186(3-4): 63-71. [ Links ]
Mäkinen, H. 1997. Possibilities of competition indices to describe competitive differences between Scots pine families. Silva Fennica 31(1): 43-52. [ Links ]
Martin, G. L. and A. R. Ek. 1984. A comparison of competition measures and growth models for predicting plantation red pine diameter and height growth. Forest Science 30(3):731-733. [ Links ]
Martínez M., F. J. y A. Madrigal. 1982. Influencia de la competencia en el crecimiento en sección. Comunicaciones INIA, Serie Recursos Naturales Núm. 13. Madrid, España. 88 p. [ Links ]
Maseda V., P. 1998. Influencia de la competencia sobre el crecimiento en sección en Quercus robur. Proyecto fin de carrera. EPS. Universidad de Santiago de Compostela. Lugo, España. 42 p. [ Links ]
Moravie M. A., M. Durand and F. Houllier. 1999. Ecological meaning and predictive ability of social status, vigour and competition in a tropical rain forest (India). Forest Ecology and Management 117(3): 221-240. [ Links ]
Munro, D. D. 1974. Forest growth models: a prognosis. In: Fries, J. (ed.). Growth models for tree and stand simulation. Royal College of Forestry, Department of Forest Yield Research. Research Note Num. 30. Stockholm, Sweden. pp. 7-21. [ Links ]
Pretzsch, H. 2009. Forest dynamics, growth and yield, from measurement to model. Springer. Heidelberg, Berlin. 664 p. [ Links ]
Pukkala, T. and T. Kolström. 1987. Competition indices and the prediction of radial growth in Scots pine. Silva Fennica 21(1): 55-67. [ Links ]
Quiñonez B., G., H. M. De los Santos P. y J. G. Álvarez-González. 2015. Crecimiento en diámetro normal para Pinus en Durango. Revista Mexicana de Ciencias Forestales 6 (29): 108-125 [ Links ]
Reineke, L. H. 1933. Perfecting a stand density index for even-aged forest. Journal of Forest Research 46: 627-638. [ Links ]
Ritchie, M. W. and D. W. Hann. 1982. Equations for predicting basal area increment in Douglas-fir and grand fir. Forest Research Laboratory, School of Forestry, Oregon State University. Research Bulletin Num. 51. Corvallis, OR, USA. 9 p. [ Links ]
Ryan, T. P. 1997. Modern regression methods. John Wiley & Sons. New York, NY, USA. pp. 285-332. [ Links ]
Statistical Analysis System (SAS) 2004. User’s Guide. SAS/STAT® 9.1. SAS Institute Inc. Cary, NC, USA. n/p. [ Links ]
Schröder, J. and K. von Gadow. 1999. Testing a new competition index for maritime pine in northwestern Spain. Canadian Journal of Forest Research 29(2): 280-283. [ Links ]
Seydack A., H. W., G. Durrheim and J. H. Louw. 2011. Spatiotemporally interactive growth dynamics in selected South African forests: Edaphoclimatic environment, crowding and climate effects. Forest Ecology and Management 261(7): 1152-1169. [ Links ]
Staebler, G. R. 1951. Growth and spacing in an even-aged stand of Douglas-fir. Master of Forestry. University of Michigan. Ann Arbor, MI, USA. 100 p. [ Links ]
Tíscar, P. A. y M. A. Tíscar. 2010. Influencia del tamaño y la competencia sobre el crecimiento en sección de Pinus nigra subsp. salzmannii y su relación con la selvicultura próxima a la naturaleza. Spanish Journal of Rural Development 1(3): 39-50. [ Links ]
Tomé, J. M. and H. E. Burkhart. 1989. Distance-dependent competition measures for predicting growth of individual trees. Forest Science 35(3): 816-831. [ Links ]
Vanclay, J. K. 1991. Mortality functions for north Queensland rainforest. Journal of Tropical Forest Science 4(1): 15-36. [ Links ]
Valles G., A. G. y R. C. Valadez C. 2006. Evaluación de índices de competencia independientes de la distancia para predecir el crecimiento de bosques mezclados en San Dimas, Durango. Revista Chapingo Serie Ciencias Forestales y del Ambiente 12(1): 39-44. [ Links ]
Wykoff, W. R., N. L. Crookston and A. R. Stage. 1982. User´s guide to the stand prognosis model. USDA Forest Service. Intermountain Forest and Range Experiment Station. General Technical Report INT-133. Odgen, UT, USA. 112 p. [ Links ]
Received: August 31, 2017; Accepted: November 17, 2017











 texto en
texto en