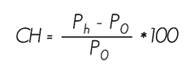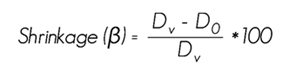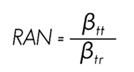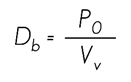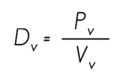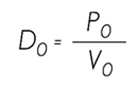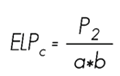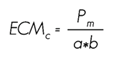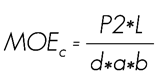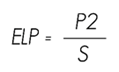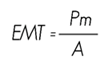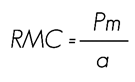Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ciencias forestales
versão impressa ISSN 2007-1132
Rev. mex. de cienc. forestales vol.8 no.40 México Mar./Abr. 2017
Articles
Physico-mechanical properties of Tectona grandis L. f. wood from a commercial plantation in the State of Michoacán
1Universidad Autónoma de Nuevo León, Facultad de Ciencias Forestales. Linares, Nuevo León. México. Correo e: telles.ricardo2015@gmail.com
2Instituto Tecnológico de El Salto. El Salto, Dgo. México.
3Campo Experimental Uruapan, Centro de Investigación Regional Pacífico Centro, INIFAP. México.
Teak has been identified as the most convenient species for establishing high quality tropical timber plantations under forest management; therefore, the physical-mechanical properties of the its wood of a commercial plantation in Nuevo Urecho, Michoacán were determined and were compared with other experiences in Mexico and other regions of the world. The plant material came from six Tectona grandis trees which were selected from their mensuration characteristics and their representativeness of each sampling site. The methodology of COPANT (1972) was followed; a log 1 meter long from the diameter of the stump (0.30 cm) was obtained from which the prisms and the test specimens were taken in order to make the physical and mechanical essays. The results of T. grandis wood show that it has a basic density of 0.59 g cm-3; categorized a s heavy wood; low volumetric shrinkage (5.15 %), which classified it as stable wood. The parallel compression, recorded a strength of 326.1 kgf cm-2 and it is classified high; perpendicular compression showed a stress of 33.6 kgf cm-2 being classified as low; in the tear or cleavage test it was observed a CMR of 44.3 kgf cm-2 being classified as mean; the shear showed a low strength value at a mean of 63.2 kgf cm-2, the lateral hardness showed average values of 545 kgf, classifying its strength as semi-hard wood. The results showed that some properties of the wood from trees planted in Nuevo Urecho, Michoacán, are remarkably similar to those of other provenances.
Key words: Compression; contraction; density; assay; timber; uses
La teca ha sido identificada como la especie potencial más conveniente para establecer plantaciones de madera tropical de alta calidad bajo manejo forestal; por ello, se determinaron las propiedades físico-mecánicas de su madera en una plantación comercial en Nuevo Urecho, Michoacán; y se compararon con otras experiencias en México y del mundo. El material vegetal procedió de seis árboles de Tectona grandis seleccionados por sus características dasométricas y representativos de cada sitio de muestreo. Se siguió la metodología de las normas COPANT (1972); de cada fuste se obtuvo una troza de 1 m de longitud a partir de la altura del tocón (0.30 cm) para elaborar los prismas y de estos, las probetas para los ensayos físicos y mecánicos. Los resultados indican que la madera de T. grandis tiene una densidad básica de 0.59 g cm-3, categorizada como madera pesada y baja contracción volumétrica baja (5.15 %), que la clasifican como madera estable. La compresión paralela registró una resistencia de 326.1 kgf cm-2 y se clasifica como alta; la compresión perpendicular mostró un esfuerzo de 33.6 kgf cm-2 que corresponde a una clase baja; en el ensayo de desgarre o clivaje, se observó una RMC de 44.3 kgf cm-2 o media; la cizalla tuvo una resistencia baja a media de 63.2 kgf cm-2, la dureza lateral alcanzó valores promedio de 545 kgf, cuya resistencia la ubica como madera semidura. Algunas propiedades de la madera procedente de las plantaciones en Nuevo Urecho, Michoacán son sensiblemente similares a las de otras procedencias.
Palabras clave: Compresión; contracción; densidad; ensayo; madera; usos
Introduction
Teak (Tectona grandis L. f.) is a tropical hardwood estimated as a high quality timber of great value in the market (ITTO, 2013). It is considered one of the most valuable in the world for its attractive appearance, natural durability and dimensional stability; its non-corrosive character is due to its natural oils, which make it resistant to termites and fungi (Fonseca, 2004). It is used for the construction of bridges and docks (for its excellent resistance to water), railway wagons and sleepers, carpentry and even for boat deck (FAO, 2010).
In Mexico, the annual timber consumption is estimated at 12.5 million m3, while local production is 9.4 million m3, which generates the need to import the differential from other countries. To compensate this deficit, commercial forest plantations have been promoted in Mexico, such as teak, which by 2014 was planted in 25 324 ha (Conafor, 2014).
The tests of the physical and mechanical properties of the woods are carried out with the purpose of proposing the probable uses and obtaining data necessary for designing and building; with such material. It is necessary that the data obtained allow the proper use of the wood in minimum proportion, and that guarantee safety in the design parameters (Hoheisel, 1981).
Research has been developed in several countries to determine the physico-mechanical properties of teakwood. In Costa Rica, Muñoz and Moreno (2013), assessed some properties of Tectona grandis L. f. and Terminalia amazonia (J. F. Gmel.) Exell wood, from commercial plantations; they evaluated lineal shinkage in radial (CR) and tangential (CT) and volumetric (CV) shinkage; the differential coefficient CT / CR or index of distortions and warps and their relationship to physical properties such as basic specific weight (PEB), fiber saturation point (PSF), normal density (DN) and moisture content (CH). In Brazil, Blanco et al. (2014) described the juvenil wood properties from plantations of the first mentioned species and compared them with data obtained from plantation woods of the same taxon in other parts of the world.
Rodríguez et al. (2014) studied the influence of age and provenance on the physico-mechanical properties of teakwood from commercial plantations in Campeche, Tabasco and Chiapas, Mexico. This information simplifies the transformation processes for end products of wood. If it is assumed that teak is an exotic species in Mexico, it is important to know its physical and mechanical behavior, since it has been considered a promising alternative for plantations in the state of Michoacán (Muñoz et al., 2011).
The aim of this work was to describe the physico-mechanical properties of the teak wood from a commercial plantation in Nuevo Urecho, Michoacán and to compare them with other national and foreign experiences.
Materials and Methods
Study área
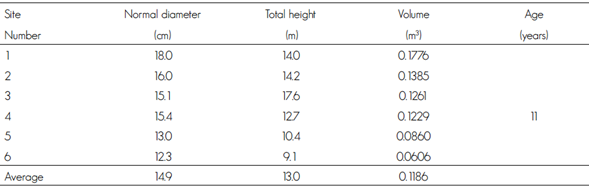
The plant material came from six Tectona grandis trees selected on the basis of their dasometric characteristics and representative of permanent sampling sites of the commercial forest plantation located in El Mirador, Nuevo Urecho municipality, Michoacán (western central Mexico). It is part of the Transverse Neovolcanic Axis, in which the El Tipítaro, Las Gallinas, Agua Fría and Cuevas hills are included (Inafed, 2010).
Its geographical coordinates are 19°1’39.6” N and 101°51’53.3” W, and an average altitude of 617 m. The main soils are Vertisol (38.32 %), Luvisol (32.24 %), Leptosol (26.08 %), Phaeozem (2.84 %), Fluvisol (0.28 %) and Regosol (0.03 %). The climatic formula is Awo (w), which describes a subhumid warm climate with summer rains, with lower humidity (91.16 %), very warm and warm semi-dry (6.93 %), warm subhumid with summer rains, sub-humid with summer rains, with medium humidity (0.51 %) and sub-humid with summer rains, with higher humidity (0.26 %); temperature range 20-28 °C and annual precipitation from 700 to 1 100 mm (Inegi, 2009).
Physical and mechanical tests were carried out at the Laboratorio de Tecnología de la Madera del Instituto Tecnológico de El Salto, Pueblo Nuevo, Durango (Wood Technology Laboratory of El Salto Technological Institute, Pueblo Nuevo, Durango). The mechanical tests were made in an INSTRON®universal machine of mechanical tests, with a 60 tons capacity.
Selection of sample tres
For the collection of the material, the recommendations of COPANT 458 standard (Pan American Technical Standards Commission) were followed, and it refers to the selection and collection of samples for the study of the physical and mechanical properties of wood. Dasometric dimensions were measured for each selected tree (Table 1).
A log of 1 meter long was cut from the stem of eachtree, starting at the stump height (0.30 cm), and then prisms were made, from which the specimens needed for the physical and mechanical tests were obtained. Each log was divided into quadrants (N, S, E, W) so that the specimens had well defined the radial and tangential planes according to the recommendations of Quiñones (1974). Each joist consisted of a 7 x 7 cm prism of cross section per 100 cm in length, which were enumerated by the number of the tree and the corresponding log. The final preparation of the specimens was performed according to the COPANT standards (Copant, 1972).
Preparation of test specimens
The test specimens were prepared in the Unidad de Tecnología de la Madera del Instituto Tecnológico de El Salto. (Wood Technology Unit of the El Salto Technological Institute). The green material for the tests was stacked indoors and conditioned until reaching 48.0 % moisture content, condition at which the final test specimens were made, 12 of 2 cm of side to determine wood density and twelve more of 5.08 x 5.08 x 10.16 cm, for shrinkage tests.
Determination of physical properties
For the design and execution of the physical tests, the methodology suggested by the standards was followed: COPANT 459 (Conditioning of woods for physical and mechanical tests); 460 (Method of determining moisture content in wood); 461 (Calculation of specific weight in woods) and 462 (Determination of contractions in woods) (Copant, 1972).
Moisture content
COPANT 460 specifies the method for determining the moisture content of wood using the following formula:
Wood shrinkage
Immediately after elaborating the specimens for the shrinkage tests, two measurement points were marked on the tangential and radial side to take the readings at the same point; they were weighed on the Ohaus EP2102C digital scale to obtain the initial weight and the dimensions of the green test pieces were measured.
They were then deposited in a Yamato DNE910 drying kiln with an initial temperature of 85 °C which increased to 105 °C during the five days in which moisture loss was monitored until constant weight was reached, and a final remeasurement of its planes in the oven-dried condition was made. Calculations were performed according to COPANT 462 standard as follows:
Wood density
The method for calculating wood density is based on the COPANT 461 standard, which suggests the dimensions that the specimens must have and the instruments to be used. For this, 12 wood samples of 2 x 2 x 2 cm were made; once removed, they were measured with a vernier and weighed on an Ohaus EP2102C digital scale.
The samples were immediately placed a Yamato DNE910 drying kiln at 105 °C where they were monitored until constant weight was obtained; afterwards, they were measured again and weighed to record anhydrous weights and volumes and thus apply the following relations:
Where:
Db |
= Basic density (g cm-3) |
P0 |
= Oven-dry (kiln dried) weight of wood (g) |
Vv |
= Green (or fully saturated) volume of test specimen (cm3) |
Where:
Dv |
= Green density (g cm-3) |
Pv |
= Green (or fully saturated) weight of wood (g) |
Vv |
= Green (or fully saturated) volume of the test specimen (cm3) |
Determination of mechanical properties
The mechanical properties of the wood are related to its behavior to the action of external or internal forces (Echenique and Robles, 1993). In order to carry out the mechanical tests, the methodology recommended in the standards was followed: COPANT 459 (Conditioning of wood for physical and mechanical tests); six different types of test specimens were prepared for parallel compression tests (COPANT 464, axial or parallel to fiber compression method) and perpendicular (COPANT 466, method of determining compression perpendicular to the fiber), perpendicular tension (COPANT 743, test method of traction perpendicular to the fiber), cleavage or tearing (COPANT 741, method of determining the resistance to cleavage or tearing), shearing or cracking (COPANT 463, determination method of parallel shear to fiber) and hardness (COPANT 465, method of determination of hardness.
Compression parallel to the fiber
For the compression test paralel to the fiber, six 20.32 x 5.08 x 5.08 cm test pieces were used. The load application was at the rate of 0.6 mm min-1. The obtained data allowed to determine the Efforts to the Proportional Limit (ELPc) and to the Maximum Load (ECMc) and the Elasticity Module (MOEc):
Compression perpendicular to the fiber
The test of compression perpendicular to the fiber was made in six 15.24 x 5.08 x 5.08 cm test specimens. The speed of the esay was 0.3 mm min-1. The corresponding calculation is the stress to the proporcionality limit:
Tension perpendicular to the fiber
The test method of tension perpendicular to the fiber was carried out with 12 5.08 x 5.08 x 6.35 cm test specimens. Half of them were made in such a way that the rupture surface was on tangential plane to the growth rings and the other half on a radial plane. The speed of load application of the test was 2.5 mm min-1. The maximum stress in tension perpendicular to grain was calculated with the maximum load supported by the stest specimen. Subsequently, a section of the breaking surface was used to calculate the moisture content:
Janka Hardness
he hardness test was performed on 6 straight prism test specimens whose dimensions were 5.08 x 5.08 x 5.08 cm. Each specimen was tested in one of the radial, tangential and transverse planes. The test consisted in introducing a hemisphere of 1 cm2 on each side, with a load application rate of 6 mm min-1, keeping it constant during the test until the total penetration of the hemisphere was reached, at which point the press stops and the test piece is removed. The penetration values are expressed directly in force kilograms.
Shear parallel to the fiber
The test specimens for the shear test were 12, 6.35 x 5.08 x 5.08 cm, cut into one of their faces. Half of them were prepared so that the plane of failure would be tangent to the growth rings and that the other half were, radial, that is, perpendicular to the tangent of the growth rings. The dimensions of the test specimens were verified at the time of the test, with the precision required according to their purpose.
The test specimen was placed in the shear device so that the 5.08 x 6.35 cm face would be parallel to the moving part and fitted to the attachment to ensure that the load applied on it produced a parallel stress closest to the shear. The speed was 0.6 mm min-1 and only the maximum load was recorded:
Cleavage
Twelve test specimens of 9.53 x 5.08 x 5.08 cm were prepared. Half of them were tested in such a way that the cleaving surface was in a tangential plane to the growth rings and the other half in a radial plane. The speed of testing was 2.5 mm min-1 ± 0.6 mm min-1 and the test continued until the crack of the test specimen occurred.
Results and Discussion
According to results obtained in the tests for physical and mechanical properties and the classification proposed by FPL (1974), Aróstegui (1980), Bárcenas (1985), IAWA (1989), Fuentes et al. (2002) and Sotomayor and Ramírez (2013), the T. grandis wood from the commercial forest plantation of Nuevo Urecho, Michoacán has the following characteristics:
Table 2 Physical properties of Tectona grandis L. f wood., Nuevo Urecho, Michoacán.
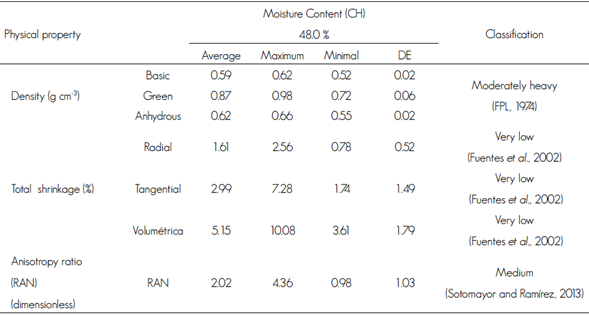
DE= Standard deviation.
Physical properties
The T. grandis wood has a basic density of 0.59 g cm-3, which classified it as heavy. In regard to the properties related to the dimensional changes, the values obtained for volumetric, tangential and radial shrinkage classify teak as stable in its dimensions, with a very low total volume shrinkage (5.15 %) (Table 2).
Table 3 shows the basic density values for planted teak woods from different origins and ages. The basic density result obtained in the present study is similar to those of other studies of teak wood from eight-year-old Bolivia plantations with 0.58 g cm-3 (Rivero and Moya, 2012) and from 21-years-old plantations of Mexico with a basic density of 0.60 g cm-3 (Rodríguez et al., 2014).
Table 3 Comparison of physical properties for Tectona grandis L. f. in studies from different sources.
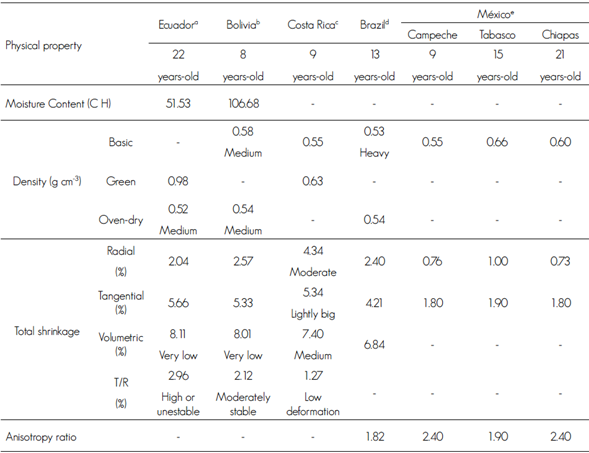
a = Gutiérrez et al., 2008; b = Rivero and Moya, 2012; c = Muñoz and Moreno, 2013; d = Blanco et al., 2014); e = Rodríguez et al., 2014.
The effect of the cambium age on the wood basic density of wood is not clearly established for many species, because it interacts with other factors such as silvicultural management, genetics, the species, geographical location, site and altitude, among others (Zobel and Van Buijtenen, 1989).
The anisotropy ratio (RAN) is an index to know the dimensional behavior of the wood during drying; by the generation of defects due to distortions and warps, the ratio the higher the occurrence probability of a distortion or deformation in the piece of wood due to the change of moisture in a drying process or when the wood is in service (Muñoz and Moreno, 2013). The differential coefficient RAN indicated that the tangential contraction is twice the radial contraction (Table 2), which coincides with that reported by Simpson and Tenwolde (1999). Rivero and Moya (2012) in Bolivia recorded an anisotropy ratio of 2.12 % and classified it as moderately stable. In plantations in Ecuador, T. grandis reached 2.96 % and Gutiérrez et al. (2008) considered it an unstable wood, while in Costa Rica, Muñoz and Moreno (2013) define it as a wood of low deformation with 1.27 %. In general, the species of this study and of other origins has similar dimensional stability.
The result of the anisotropy relationship for the wood of species showed a value of 2.02 (Table 2), which according to Sotomayor and Ramírez (2013) is classified as medium; according to Silva et al. (2010), dimensional stability is a useful qualitative term to qualify the dimensional movement of the wood exposed to cyclical changes of relative air relative humidity and temperature. The lower the anisotropy values, the greater stability of the wood is inferred. This value coincides with the results obtained for teak wood from plantations evaluated by Blanco et al. (2014) in Brazil, obtaining an average anisotropy ratio of 1.82 (Table 3); and for the studies carried out in southeastern Mexico, Rodríguez et al. (2014) mention that the classification of anisotropy ranges from medium to high (Table 3).
Mechanical properties
One of the main functions of the wood in the stem and branches of the living tree is that of mechanical support, so once this raw material has been transformed into a product, this property continues to play an essential role in many forms of use.
Compression parallel occurs when a force acts parallel to the fibers and corresponds to the resistance that opposes a column to a load applied in the same direction of the direction of the fiber. The results of the test on Tectona grandis wood at age 1 revealed showed a maximum compressive stress of 326.1 kgf cm-2, which is classified as high (Dávalos and Bárcenas, 1998) (Table 4). This value was similar to that reported by Rivero and Moya (2012), in which MOR was 460.6 kg cm-2, and also classified as high for an age of eight years (Table 5).
Table 4 Mechanical properties of Tectona grandis L. f. wood in Nuevo Urecho, Michoacán.
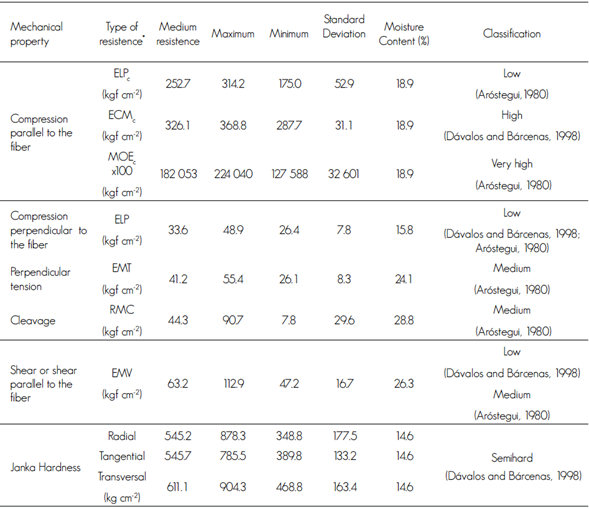
*ELPc = Stress at the Proportional Limit; ECMc= Stress to Maximum Load; MOEc = Modulus of Elasticity; ELP: Stress at the Proportional Limit; EMT= Maximum stress in tension perpendicular to the fiber; RMC= Maximum cleavage strength; EMV= Maximum stress in shear parallel to grain; DE= Standard Deviation.
Cuadro 5 Average values of the mechanical properties of Tectona grandis L. f. wood in several studies from different provenances.
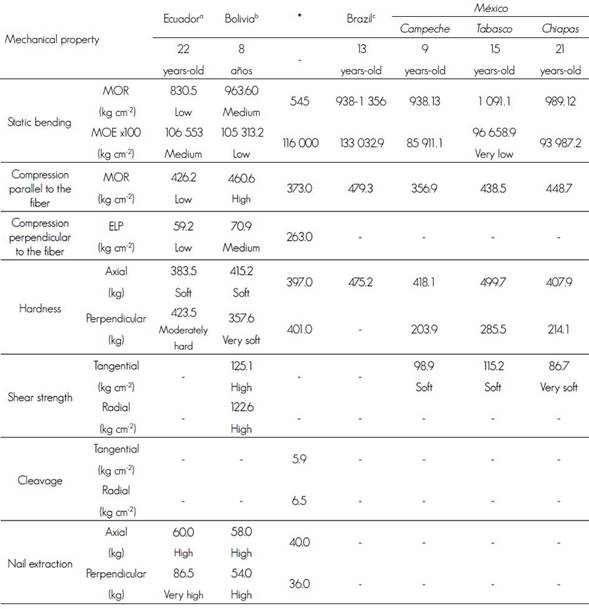
MOR = Modulus of Rupture; MOE = Modulus of Elasticity; ELP = Stress at the Proportional Limit. a = Gutiérrez et al., 2008; b = Rivero and Moya, 2012; c = Blanco et al., 2014; d = Rodríguez et al., 2014. * = Moya et al., 2012.
Compression perpendicular occurs when the force acting in the direction perpendicular to the fibers and corresponds to the resistance that a piece of wood opposes to a load applied perpendicular to the direction of the fibers on a radial face of the specimen (Table 4). The stress at the proportional limit of 33.6 kgf cm-2 derived from the perpendicular compression test in Tectona grandis wood, classifies it as low (Dávalos and Bárcenas, 1998; Aróstegui, 1980). Regarding the results of other studies of teak, Gutiérrez et al. (2008) report an ELP value of 59.2 kg cm-2 for plantations of 22 years old; these figures differ from those of Moya et al. (2012) who established that the perpendicular compression value of the PLA was 263.0 kg cm-2 (Table 5).
The strength of the wood to forces acting perpendicular to the fiber and tending to separate a piece of wood is called stress perpendicular to the fiber. The results of the test in tension perpendicular to the fiber showed maximum tensile stress (EMT) of 41.2 kgf cm-2 which places this property as average according to Aróstegui (1980) (Table 4). This information is useful to the furniture industry for calculating the mechanically connected wood assembly.
The wood cleavage test indicates a CMR of 44.3 kgf cm-2 which, according to Aróstegui (1980), is classified as medium (Table 4). This value is much higher than the values of cleavage found by Moya et al. (2012), from 5.9 to 6.5 kg cm-2 who qualified it as low (Table 5).
With respect to the Tectona grandis wood shear test, the maximum stress of 63.2 kgf cm-2, which according to Dávalos and Bárcenas (1998) and Aróstegui (1980) (Table 4). This value is lower than those of Rodríguez et al. (2014) in plantations from southeastern Mexico ranging from 86.7 to 15.2 kgf cm-2 and, according to the Prospect (1997) classification, 9 and 15 year old wood is classified as soft, and that 21 years old, as very soft.
The hardness test recorded average values of 545 kgf for the wood side planes (tangential and radial), which allows to classify the hardness strength of the studied wood within the range of the semi-hard; while for the end-sides (transverse), values of 61 kgf were observed, confirming their classification according to Dávalos and Bárcenas (1998) (Table 4). The indicated hardness values are higher than those from Ecuador calculated by Gutiérrez et al. (2008); in Bolivia by Rivero and Moya (2012) and to those of the Mexican southeast by Rodríguez et al. (2014); all these authors coincide in describing Tectona grandis as a soft to very soft wood (Table 5).
Conclusions
The 1-year-old Tectona grandis species from the Nuevo Urecho plantation, Michoacán, had a mean value of 0.59 g cm-3 of basic density, without any clarity in the effect of age on the basic density from their interaction with other factors.
The results showed that some properties of the wood approach those of teak woods in studies of other sources, such as the total volumetric shrinkage that was very low (5.15 %) considered of stable stability in its dimensions. For the parallel compression a resistance of 326.1 kgf cm-2 was observed, which is classified as high.
The hardness test (545 kgf) allows to classify its resistance within the range of semi-hardwoods.
The former results apply mainly to the area of Nuevo Urecho, Michoacán and the previously studied plantation and management conditions since the physical and mechanical properties can be affected by local climate, soil, management and structural characteristics.
Acknowledgements
The authors would like to express their gratitude to the Instituto Nacional de Investigaciones Forestales Agrícolas y Pecuarias, in particular to the Campo Experimental Uruapan for their support through its technical personnel and by providing the study materials. Also, to the Instituto Tecnológico de El Salto, P.N., Durango, for lending its equipment
REFERENCES
Aróstegui, V. 1980. Propiedades tecnológicas y uso de la madera de 40 especies del Bosque Nacional Alexander Von Humboldt. Revista Forestal del Perú 10(1-2): 3-82. [ Links ]
Bárcenas P., G. M. 1985. Recomendaciones para el uso de 80 maderas de acuerdo con su estabilidad dimensional. Instituto de Investigaciones sobre Recursos Bióticos (INIREB), Laboratorio de Ciencia y Tecnología de la Madera (LACITEMA). Xalapa, Ver., México. 18 p. [ Links ]
Blanco F., J., P. F. Trugilho, J. T. Lima, P. R. Gherardi H. y J. R. Moreira da S. 2014. Caracterización de la madera joven de Tectona grandis L. f. plantada en Brasil. Madera y Bosques 20(1): 1-20. [ Links ]
Comisión Nacional Forestal (Conafor). 2014. Principales especies, maderables establecidas en PFC por año para el periodo 2000-2014. http://www.conafor.gob.mx:8080/documentos/docs/43/6019Principales%20 especies%20maderables%20establecidas%20en%20PFC%20por%20Entidad%20Federativa%20en%202000%20-%202014.pdf (10 de marzo de 2016). [ Links ]
Comisión Panamericana de Normas Técnicas (Copant) 1972. Madera- Selección y colección de muestras (458, 459, 461, 462, 555, 464, 466, 742, y 743). Buenos Aires, Argentina. s/p [ Links ]
Dávalos S., R. y G. M. Bárcenas P. 1998. Clasificación de las propiedades mecánicas de las maderas mexicanas en condición “verde”. Madera y Bosques 4(1): 65-70. [ Links ]
Echenique M., R. y V. F. Robles F. 1993. Ciencia y Tecnología de la madera I. Textos Universitarios de la Universidad Veracruzana. Veracruz, Ver., México.137 p. [ Links ]
Fonseca G., W. 2004. Manual para productores de teca (Tectona grandis L. f) en Costa Rica. Heredia, Costa Rica. 121 p. [ Links ]
Food and Agriculture Organization of the United Nations (FAO). 2010. La teca: una visión global. http://ftp.fao.org/docrep/fao/x4565s/X4565s02.PDF (10 de marzo de 2016). [ Links ]
Forest Products Laboratory (FPL). 1974. Wood handbook: wood as an engineering material. USDA General Technical Report FPL- GTR-190. USDA Forest Service. Madison, WI, USA. 508 p. [ Links ]
Fuentes, F., J. Silva, M. Lomelí, H. Ricther y R. Sanjuán. 2002. Comportamiento higroscópico de la madera de Persea americana var. guatemalensis Mill (Hass). Revista Chapingo Serie Ciencias Forestales y del Ambiente 8(1): 49-56. [ Links ]
Gutiérrez R., C., J. Romero E., S. Cunuhay P., L. Blanco G. y S. Fonseca C. 2008. Análisis comparativo de las propiedades físico-mecánicas de la madera de teca (Tectona grandis L. f.) de Quevedo y Balzar. Revista Ciencia y Tecnología 1(2): 55-63. [ Links ]
Hoheisel, H. 1981. Estipulaciones para los ensayos de propiedades físicas y mecánicas de la madera. Universidad Nacional de Los Andes. Facultad de Ciencias Forestales. Mérida, Venezuela. 51 p. [ Links ]
Instituto Nacional de Estadística Geográfica e Informática (Inegi). 2009. Prontuario de información geográfica municipal de los Estados Unidos Mexicanos. Nuevo Urecho, Michoacán de Ocampo. Clave geoestadística 16059. www.inegi.gob.mx . In: In: http://www3.inegi.org.mx/sistemas/mexicocifras/datos-geograficos/16/16059.pdf (12 de marzo de 2017). [ Links ]
Instituto Nacional para el Federalismo y el Desarrollo Municipal (Inafed). 2010. Michoacán de Ocampo., México. http://www.inafed.gob.mx/work/enciclopedia/EMM16michoacan/index.html (24 de febrero de 2016). [ Links ]
International Association of Wood Anatomy (IAWA). 1989. List of microscopic features hardwood identification. IAWA Bulletin 10(3): 220-359. [ Links ]
International Tropical Timber Organization (ITTO) . 2013. World Teak Conference. Bangkok, Thailand. http://www.itto.int/news_releases/id=3376 (10 de marzo de 2016). [ Links ]
Moya R., R., F. Muñoz A., C. Salas G., A Berrocal J., L. Leandro Z. y E. Esquivel S. 2012. Tecnología de madera de plantaciones forestales: Fichas técnicas. Revista Forestal Mesoamericana Kurú 7(18-19): 1-217. [ Links ]
Muñoz A., F. y P. A. Moreno P. 2013. Contracciones y propiedades físicas de Acacia mangium Willd., Tectona grandis L. f. y Terminalia amazonia A. Chev, maderas de plantación en Costa Rica. Revista Chapingo. Serie Ciencias Forestales y del Ambiente 19(2): 287-304. [ Links ]
Muñoz F., H. J., J. T. Sáenz R. y A. Rueda S. 2011. Especies promisorias de clima tropical para plantaciones forestales comerciales en Michoacán. Libro Técnico Núm. 11. SAGARPA-INIFAP-CIRPAC-Campo Experimental Uruapan. Uruapan, Mich., México. 202 p. [ Links ]
Prospect. 1997. The wood database. Version 2.1. Oxford Forestry Institute. London, UK. n/p. [ Links ]
Quiñones J., O. 1974. Características físicas y mecánicas de la madera de cinco especies mexicanas. Instituto Nacional de Investigaciones Forestales. Bol. Téc. Núm. 42. México, D. F., México.19 p. [ Links ]
Rivero M., J. y R. Moya R. 2012. Propiedades físico-mecánicas de la madera de Tectona grandis Linn. F. (teca), proveniente de una plantación de ocho años de edad en Cochabamba, Bolivia. Revista Forestal Mesoamericana Kurú 3(9): 50-63. [ Links ]
Rodríguez A., R., J. F. Zamora N., J. A. Silva G., E. Salcedo P. y F. J. Fuentes T. 2014. Propiedades físico-mecánicas de madera de teca de plantaciones comerciales. Revista Mexicana de Ciencias Forestales 5(24): 12-25. [ Links ]
Silva G., J. A., F. J. Fuentes T., R. Rodríguez A., Torres, A. P. A., M. G. Lomelí R., J. Ramos Q., C. Waitkus y H. Richter G. 2010. Fichas de propiedades tecnológicas y usos de maderas nativas de México e importadas. Universidad de Guadalajara. Guadalajara, Jal. México. 207 p. [ Links ]
Simpson, W. and A. Tenwolde. 1999. Physical properties and moisture relations of wood. In USDA Forest Products Staff (eds.). Wood handbook: wood as an engineering material. U. S. Department of Agriculture, Forest Service, Forest Products Laboratory. General Technical Report FPL-GTR-13. Madison, WI, USA. Vol. 3. pp. 3-23. [ Links ]
Sotomayor C., J. R. y M. Ramírez P. 2013. Densidad y características higroscópicas de maderas mexicanas. Base de datos y criterios de clasificación. Investigación e Ingeniería de la Madera 9(3): 3-29. [ Links ]
Zobel, B. and P. Van Buijtenen J. 1989. Wood variation, its causes and control. Springer-Verlag. Berlin, Germany. 363 p. [ Links ]
Received: January 18, 2017; Accepted: March 06, 2017











 texto em
texto em