SciELO - Scientific Electronic Library Online
 
vol.9 número6Propiedades fisicoquímicas de guayabilla (Psidium guineense), arrayán (Psidium sartorianum) y guayaba (Psidium guajava)Respuesta del clon mexicano de papa 99-39 a potasio en hidroponía e invernadero índice de autoresíndice de materiabúsqueda de artículos 		Home Pagelista alfabética de revistas  

Servicios Personalizados

Revista

Articulo

Indicadores

Links relacionados

  • No hay artículos similaresSimilares en SciELO

Compartir

Revista mexicana de ciencias agrícolas

versión impresa ISSN 2007-0934

Rev. Mex. Cienc. Agríc vol.9 no.6 Texcoco ago./sep. 2018

https://doi.org/10.29312/remexca.v9i6.1577 

Articles

Analytical expressions of soil erosion and impact on their productivity

Ignacio Sánchez Cohen1 

Aurelio Pedroza Sandoval2  § 

Miguel A. Velásquez Valle3 

Palmira Bueno Hurtado1 

Gerardo Esquivel Arriaga1 

1INIFAP-National Center for Disciplinary Research in Water-Soil-Plant-Atmosphere Relationship. Right bank channel Sacramento km 6.5, Gómez Palacio industrial zone, Durango. CP. 35140. Tel. 01(871) 1590105.

2Autonomous University Chapingo-Regional University Unit of Arid Zones. Dom. Acquaintance, Bermejillo, Durango. Tel. 01(872) 7760160.

3INIFAP-Northeast Regional Research Center. Experimental Field Saltillo. Carretera Saltillo-Zacatecas km 342 + 119, num. 9515, Hacienda de Buena Vista, Saltillo, Coahuila. CP. 25315. Tel. 01(55) 38718700.

Abstract

The approximations for the estimation and projection of soil loss in hydrological basins, vary from the empirical equations, to the use of models based on environmental physics. The objective of this study was to generate and propose the use of a logistic differential equation for estimating soil loss. By using an exponential model under conditions of soil deterioration, the yield loss of the corn crop was estimated at 3.5 t ha-1, going from 4.5 to 1 t ha-1. The erosion model was parameterized with information from an experimental INIFAP basin located in the municipality of San Luis of Cordero, Durango. The results indicate that the average annual rate of soil loss is 0.44 mm year-1, for which it was considered a critical rate of soil loss of 10 mm year-1. With that initial rate, the range would reach its maximum allowable rate in 19 years. This study analyzes the behavior of the model parameters from where other soil loss scenarios were tested where the maximum permissible rate is reached at different times.

Keywords: environmental impact; process modeling; soil loss; yield

Resumen

Las aproximaciones para la estimación y proyección de pérdida de suelo en cuencas hidrológicas, varían desde las ecuaciones empíricas, hasta el uso de modelos basados en la física ambiental. El presente estudio tuvo como objetivo generar y proponer el uso de una ecuación diferencial logística para la estimación de pérdida de suelo. Mediante el uso de un modelo exponencial bajo condiciones de deterioro del suelo, se estimó la pérdida de rendimiento del cultivo maíz en 3.5 t ha-1 al pasar de 4.5 a 1 t ha-1. El modelo de erosión se parametrizó con información de una cuenca experimental del INIFAP situada en el municipio de San Luis del Cordero, Durango. Los resultados indican que la tasa promedio anual de pérdida de suelo es de 0.44 mm año-1, para lo cual se consideró como tasa crítica de pérdida de suelo 10 mm año-1. Con esa tasa inicial, el agostadero alcanzaría su tasa máxima permisible en 19 años. Este estudio analiza el comportamiento de los parámetros del modelo de donde se ensayaron otros escenarios de pérdida de suelo donde la tasa máxima permisible se alcanza en diferentes tiempos.

Palabras clave: impacto ambiental; modelación de procesos; pérdida de suelo; rendimiento

Introduction

Soil losses in watersheds is a recurring problem in hydrological studies faced by natural resource users and the researchers themselves. These losses have effects in situ and ex situ of the affected basins. In situ problems include the loss of soil structure, the decrease of soil organic matter and nutrients, and the reduction of water availability in the soil (Brooks et al., 2012). Ex situ effects increase the transport of sediments and the loss of nutrients such as nitrogen and phosphorus that are adhered to eroded soil particles deposited in the drainage network of the basins, below where the problem arises.

The increase of sediment in the drainage network of the basins reduces the transport capacity and reduces the quality of the water that drains downstream where it is used for different uses (Ffolliot et al., 2013). Also, the loss of soil due to water erosion is the main factor that limits the productivity of soils that obstructs full production in agriculture (Obalum et al., 2012). Population growth and change in land use exacerbate the process along with high rainfall intensities, mainly in arid areas (FAO, 1995).

The selection of the method for sizing or quantifying soil losses in watersheds is then of crucial importance (Wainwright and Mulligan, 2004). To estimate the process of soil erosion, several approaches have been proposed and currently there are several models for this purpose, which can be classified in different ways. According to Van der Knijff (2000), a subdivision can be made based on the time scale in which the model operates, so some models are designed to estimate soil losses in the long term and others to estimate erosion by event of rain. In this last category, you can find the Kineros2 model (Goodrich et al., 2012) and SWAT (Arnold et al., 2012). Another useful approach in the process of selecting the method to quantify erosion is between empirical models and physically based models (Sánchez, 2005). The optimal selection of a model must be based on the answer to the questions: What do you want to do? With what level of precision and scale? and What is the information available? If you omit this, you run the risk of over or under using the capabilities of the different simulation models.

Materials and methods

The analysis of this work is based on the growth equation proposed by Malthus and described by Pearl and Reed (1920). The differential equation described is:

dNdt= rN 1)

Where: N is the population and 't' is time. The differential equation establishes that the variation of the population through time is proportional to the same population; that is, if the population is large then its variation in time will also be large. Equation 1 is separable in mathematical terms and its solution consists of grouping similar terms on one side of equality and the remaining on the other; so equation 1 is translated into equation 2 by dividing everything between 'N' (what the term 'N' disappears from the right side of equality) and multiplying by 'dt' (what disappears the 'dt' from the left side of equality:

1NdN= rdt 2)

Obtaining the anti-derivative (integrating) of equation 2 we obtain:

∫1NdN=∫rdt= lnN= rt+c 3)

Where:

N=ert+c=ert ec=ertC 4)

Assuming that the population will never be negative, then the absolute value of N disappears; so also, eC is an arbitrary constant ‘C’. In this way, equation 4 is the solution to the differential equation 1. In this equation, ‘r’ is the population growth rate.

In terms of soil erosion, equation 4 can be valid as long as the soil loss is below a maximum value (K) dictated by the depth of the soil; that is, at this point, there would be no loss of soil since it would have been completely exhausted. The constant ‘C’ of equation 4 can be seen as the initial loss of soil at time ‘0’ [N(0)] ; so if t= 0 when replacing this value in that equation, it turns out that N(0)= 0= C since e0 =1.

After the work of Malthus, Verhults (1845); Bacaer (2011) proposed a growth equation implying that population growth could not be exponential, since it would reach a limit where the ecosystem could no longer maintain it and at that point it would become asymptotic at the time. The differential equation proposed by Verhults is: (Wlofram, 2002; Skoldberg, 2012).

dNdt= rN 1-NK 5)

According to Thornes (2004), this differential equation can be used for the modeling of the erosion process when an initial soil loss or loss and the upper limit of maximum erosion are known, after which the productivity of the crops decreases. The rational use of the logistic function can be summarized in that the more erosion there is, the more erosion there will be. This process begins slowly, then acquires an exponential behavior, then decrease until reaching an equilibrium. The cyclicity of this process (positive feedback) occurs because thin soils produce more runoff; therefore, more erosion and consequently thinner soils. The rate of erosion is eventually reduced as more soil has been removed. This reduction occurs mainly because the deeper soil horizons are denser and have a higher stony content. Finally, when there is no longer soil, no more erosion can occur, so the maximum loss of soil that can be reached is given by its depth.

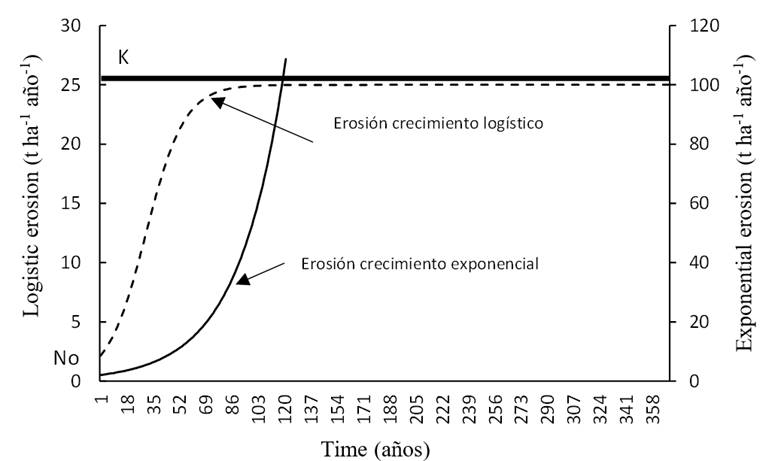
The term 1‒NK of equation 5 can be reasoned as follows: Let ‘N’ be the initial value of the erosion (it can be rate or it can be volume) and ‘K’ the maximum value of soil loss; then when the initial erosion (N) is close to 0, soil erosion can be described by equation 4; on the other hand, if the erosion approaches the maximum value ‘K’, then the erosion is 0 given that there would be no more soil to erode and it constitutes the asymptotic part of the upper dashed line of Figure 1.

Figure 1 Graphical solution to the differential equations 4 (continuous line) and 5 (dashed line) for the erosion process. 

The equation 5 is a separable differential equation, so (Gershenfeld, 1999; Stewart, 1996):

dNdtN1-NK=r=1N1-NK dNdt 6)

The equation 6 can be integrated using the partial fraction expansion solution scheme:

AN+B1-NK=1N1-NK 7)

Where:

A-ANK+NB=1N1-NK 8)

By the method of coefficient equalization, it have that A= 1 and B=1K; thus substitute these values in equation 6, leaving:

1N+1K1-NK dNdt= r 9)

Expanding equation 9 and integrating, it results:

∫1NdNdt+∫1K1-NKdNdt=∫r 10)

ln⁡N-ln⁡1-Nk+C= rt+C 11)

In the numerator on the right side of the equality + 0N is added so the coefficients of N on the left side are equal to that on the right side; so then AKand B= 0 and A= 1; the value of A is substituted, leaving -1K+B= 0, so B =1K.

If it is assumed that soil erosion is not negative and moves in the range 0< N (t)< K, then the operand of the absolute value disappears leaving:

ln⁡N-ln⁡1-NK= rt+c 12)

According to the properties of the logarithms we obtain:

lnN1-NK= rt+C 13)

Obtaining the natural logarithm on both sides of equality:

N1-NK=ert+c=ert ec=ertC 14)

Solving for N by taking the reciprocal of equation 14:

1-NKN= Ce-rt=1N-1K 15)

Adding 1K on both sides of the equality is:

1N= Ce-rt+1K 16)

Taking the reciprocal from both sides you have to:

N(t)=1Ce-rt+1K 18)

Assuming that erosion at time 0 is N0, then at time 0:

N0=1C+1K 19)

Taking the reciprocal of equation 19 we have:

C+1K=1N0 20)

Where:

C=1N0-1K 21)

Substituting the value of the constant ‘C’ in equation 18:

Nt=11N0-1ke-rt+1K 22)

Reducing terms you have to multiply numerator and denominator by N0K.

Nt=N0KK-N0e-rt+N0 23)

Equation 23 is the solution to the differential equation 5. er(0)= 1.

Parameterization of the logistic model

The logistic model of erosion (equation 23) considers three parameters in its structure: the rate of erosion ‘r’, the initial state of erosion (No) and the maximum erosion or maximum erosion limit (K) (Figure 1).

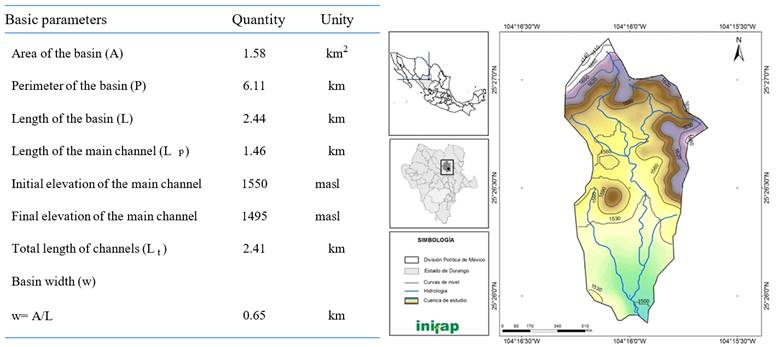
The model operates on any time scale ‘t’, for the case of erosion and in order to obtain an objective assessment of what the loss of soil in some locality might be, the annual scale is recommended. So, to obtain the parameter ‘r’; it is necessary to have data of erosion field observed over time. For the experimental basin of the INIFAP in the municipality of San Luis of Cordero, an annual soil loss of 0.33 mm (r) has been estimated. The characteristics of the basin are shown in Figure 2 and Table 1.

Figure 2 Parameters of the San Luis of Cordero basin, Durango. 

Table 1 Components of the surface state in the experimental basin. 

Coverage (%)
Rock 26.85
Soil 52.4
MO 4.44
Vegetation 15.92

The parameter ‘K’, can be established as the maximum rate of soil loss that can be accepted in a conservationally sized temporary survey. In the case of the basin mentioned above, it is estimated that the loss of soil should not exceed 10 mm in order not to reduce the productive capacity of wild flora, which includes native grasses, since it is the main source of entry to localities by cattle grazing.

Loss of productivity

The differential equation 5, counts the time in which a certain amount of soil would be lost according to the erosion rate and the maximum limit imposed. This reduction in available amount of soil directly impacts the productivity of crops in arid zones.

In temporary zones, crop yields are strongly associated with the presence of climatic events (random nature) for their optimal development; thus, the erosion process follows the same variations as rainfall. Hence, it is pertinent to visualize the productivity of soils as a consequence of climatic factors (Sánchez, 1995).

According to Todorovic et al. (1987), the relation between the yield of a crop in a given year (Yn) and the yield of the same crop under a soil subjected to erosion (Xn), is given by:

Xn=Yna +(1-a)dnD;dn< D 24)

In the above equation, the parameter ‘a’ is XnYn, dn is the available soil and ‘D’ is the thickness of the upper or arable layer. The rate of soil loss would be given by:

r=eD 25)

Where: ‘e’ is the annual loss of land. So then, the available floor ‘dn’ will be degraded according to:

dn= D(1-r)n 26)

In the above equation ‘n’ indicates the year number. If equation 26 is substituted in equation 24, we have:

Xn=Yna + (1-a)(1-r)n 27)

The above equation quantifies the Xn yield that would be expected in the nth year under a constant erosion rate ‘r’ and based on the expected Yn crop yield.

Randomness of performance

As has been established, the randomness of crop yields in rainfed areas strictly follows the randomness of rainfall. Considering performance varies randomly with μ mean and standard deviation σ can be generated then stochastically crop yields as:

Yn= μ + σz 28)

Being z:

z=-2ln(rnd1)0.5cos2π(rnd2) 29)

Where: rnd1, 2 are random numbers with μ= 0 and σ= 1.

Parameterization of the productivity model

The parameter ‘a’ of equation 27 is the quotient between crop yield under non-erosion conditions (naturally preserved soil, Xn) and crop yield under eroded soil. These values can be obtained from empirical experience or resort to literature in the context. Thus, Table 2 shows guide values to obtain this value.

Table 2 Reduction of the yield in the corn crop due to the loss of soil (Mokma and Siez, 1992). 

Degree of erosion Average performance (t ha-1)
Light 7.34
Moderate 7.09
Severe 5.83

Other authors such as Mbagwu (1988) obtained functional relationships between maize crop yield and soil erosion in plots with induced erosion. For the first year of study he found:

Ya = 33.2761e−0.1621x with R2= 0.998 and for the second: Yb = 11.6116e−0.1489x with R2= 0.985. In these regressions ‘x’ is the soil erosion expressed in cm and Ya, Yb are the annual yields (t ha-1).

For the quantification of the parameter ‘r’, it is necessary to establish the thickness of the soil layer that is interesting to conserve (D), usually this can be defined by the arable layer (in seasonal and irrigation agriculture) or that layer capable of being eroded more easily in pastures. On the other hand, the parameter ‘e’ of equation 25 is the current erosion rate: for example, as already noted, in the experimental basin of INIFAP in the municipality of San Luis of Cordero, Durango, the observed rate of erosion during 2016, in three events is 0.44 mm year-1 on average. The previous thing after analyzing the sedigrams (variation of the solids in suspension in the time measured in the runoff), product of rainy events (Figure 3).

Figure 3 Sampling to determine the concentration of suspended solids in a runoff event during August 2016. INIFAP experimental basin, San Luis of Cordero, Durango. 

However, given the lack of this value, the model can be manipulated with different erosion rates and soil depths to verify what would be the loss in productivity of the crop in different management scenarios.

Results and discussion

With the information of the experimental basin described above with an initial erosion rate of 0.33 mm year-1 and presetting a maximum permissible rate of 10 mm year-1, using equation 23 which is the numerical solution of the differential equation 5, If the erosion rate remains constant over time, the soil will have reached its maximum allowable in a period of 20 years (upper part of Figure 4) with an impact on the productivity of the corn crop going from 4.5 t ha-1 to 2.5 t ha-1 (bottom of Figure 4).

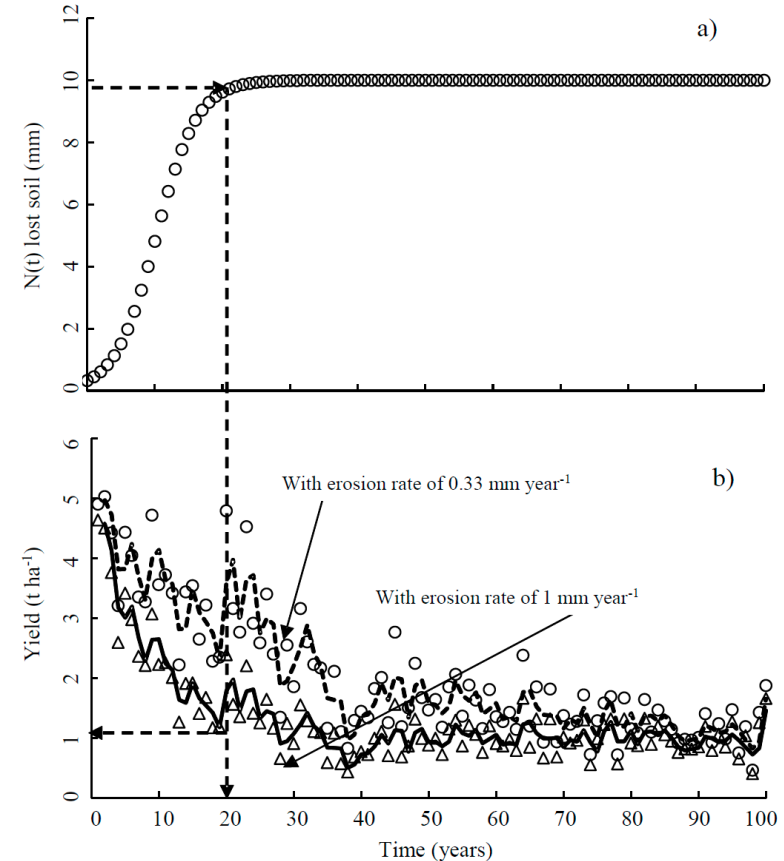
Figure 4 Model assembly. Logistic model for the prediction of abatement of soil depth by erosion (A) and time series of loss of soil productivity and its impact on maize crop yield (B). 

On the other hand, if the rate of soil loss is 10 mm year-1, then productivity would fall to 1.2 t ha-1. The time series that indicates the lower part of Figure 4 was obtained by means of equations 24 and 25 in a simulation process of one hundred years for two erosion rates 0.33 and 10 mm year-1. Based on the above, a computer program was generated, codified in Fortran 90, to systematize this process by randomizing the production of the corn crop (equations 28 and 29).

The loss of productivity is a reflection of the loss of soil depth with the consequent reduction in moisture retention and fertility.

Analysis of model parameters

Once the parameters of the differential equation have been obtained, estimates of soil loss and productivity can be made under different management scenarios. Figure 5 presents the form of the solution of the differential equation when considering different initial rates of erosion (N0= 0.1, 0.4 and 2) keeping the rate of erosion constant over time (r= 0.44).

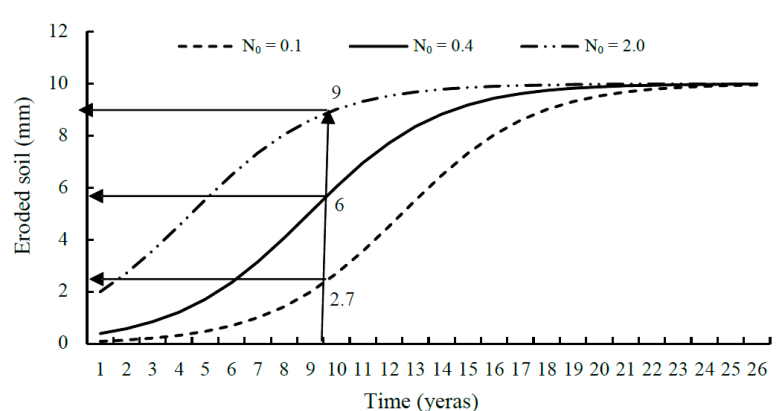
Figure 5 Variation of soil loss considering different initial erosion rates (parameter N0 of equation 23). 

From Figure 5 the importance of the initial erosion rate in the degradation of the soil circumscribed in time can be appreciated. For the case of the INIFAP experimental basin, in case this erosion rate is maintained (0.44 mm of soil lost per year), in a period not exceeding 20 years the 10 mm of soil that was imposed on the soil would have been eroded. The basin as permissible. The graph shows the amount of soil that would be lost over a period of nine years for different initial erosion rates, for the case of the experimental basin, the loss would be 6 mm of soil.

Figure 6 shows the impact of the erosion rate on time (r) in the form of the solution of the differential equation 5, thus the higher the erosion rate (r= 4 mm year-1), the faster it will be reached the allowable limit of soil loss for the study basin.

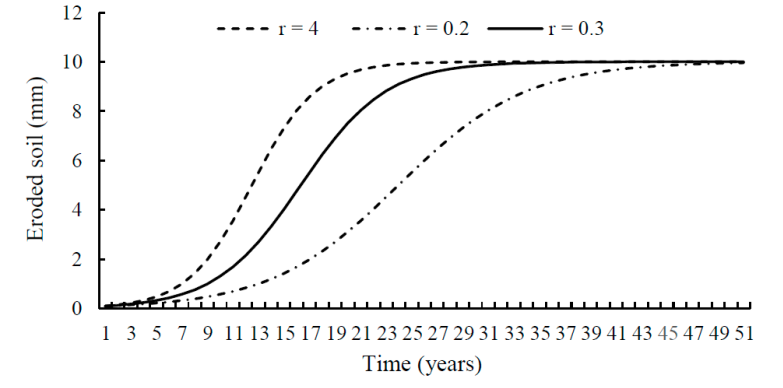
Figure 6 Variation of soil loss considering different erosion rates (parameter ‘r’ of equation 23) with constant initial rate. 

Both the Malthusian exponential model and the Verhults Logistic model (Figure 1) assume that the erosion rate is proportional to the magnitude of the problem (greater erosion drivers, assumes a higher rate of erosion, this is the basic assumption for the solution of the differential equation that defines the phenomenon). However, the logistic model also assumes that erosion depends on the availability of soil (parameter 1-NK of equation 5), so that exponential growth is limited to low soil availability. When the depth of soil susceptible to being eroded disappears, then the erosion rate is reduced to zero, reaching a stable condition, situating itself in its erodable capacity (K).

Conclusions

A logistic differential equation is proposed for the projection of soil loss due to water erosion. The result of erosion, is used to quantify the impact on the productivity of the corn crop in areas with deficient weather subject to the erosion process. Although, according to the literature, the logistic equation has not been widely used to explain the erosion process, on this occasion it is presented as an option for this objective in strict adherence to the assumptions of the model and in the geometry presented by the functions of soil erosion in the field. The model considers three parameters that can be quantified with information measured directly in the field or, as a first approximation, with data from literature. Its use is recommended when availability and information is scarce and it is desired to have an appreciation of the impact of soil loss on the productivity of pastures and/or annual crops.

Literatura citada

Arnold, J. G.; Moriasi, D. N.; Gassman, P. W.; Abbaspour, K. C.; White, M. J.; Srinivasan, R.; Santhi, C.; Harmel, R. D.; Van, G. A.; Van, L. M. W.; Kannan, N. and Jha, M. K. 2012. Swat: model use, calibration, and validation. ASABE. 55(4):1491-1508. [ Links ]

Bacaër, N. 2011. A Short history of mathematical population dynamics. Springer-Verlag London Limited. London. 160 p. DOI 10.1007/978-0-85729-115-86. [ Links ]

Brooks, K. N; Pfolliott. F. F. and Magner J. A. 2012. Hydrology and the management of watersheds. 4th Edition. John Wiley & Sons, Inc., New York. 552 p. [ Links ]

FAO. 1995. Land and environmental degradation and desertification in Africa, FAO Corporate Document repository. URL: http://www.fao.org/docrep/x5318e/x5318e00.htm#Contents. [ Links ]

Ffolliott, P. F.; Brooks, K. N.; Tapia, R. P.; Chevesich, P. G. and Neary, D. G. 2013. Soil erosion and sediment production on watershed landscapes: processes, prevention, and control. UNESCO. Documentos técnicos del PHI-LAC, No. 32. 70 p. [ Links ]

Gershenfeld, N. A. 1999. The nature of mathematical modeling. Cambridge, UK. Cambridge University Press. 356 p. [ Links ]

Goodrich, D. C.; Burns, I. S.; Unkrich, C. L.; Semmens, D. J.; Guertin, D. P.; Hernández, M.; Yatheendradas, S.; Kennedy, J. R. and Levick, L. 2012. Kineros2/AGWA: model use, calibration and validation. Transactions of theASABE . American Society of Agricultural and Biological Engineers. 55(4):1561-1574. [ Links ]

Mbagwu, J. S. C. 1988. Physico-chemical properties and productivity of an Ultisol in Nigeria as affected by long-term erosion. Pedologie. 38(2):137-154. [ Links ]

Obalum, S. E.; Buri, M. M.; Nwite, J. C.; Watanabe, Y.; Igwe, C. A. and Wakatsuki, T. 2012. Soil degradation-induced decline productivity of sub-saharan african soils: the prospects of looking downwards the lowlands with the sawah ecotechnology. Appl. Environm. Soil Sci. 10 p. doi: 10.1155/2012/673926. [ Links ]

Pearl, R. and Reed, L. J. 1920. On the rate of growth of the population of the United States since 1790 and its mathematical representation. Proc. Natl. Acad. Sci. 6:275-288. http://www.pnas.org/search?fulltext=pearl+and+reed&submit=yes&x=0&y=0. [ Links ]

Sánchez, C. I. 1995. Erosión y productividad en la Comarca Lagunera. Folleto científico núm. 4. INIFAP ORSTOM. 25 p. [ Links ]

Sánchez, C. I. 2005. Fundamentos para el aprovechamiento integral del agua. Una aproximación de simulación de procesos. Libro científico núm. 2. INIFAP CENID RASPA. 272 p. [ Links ]

Skoldberg, E. 2012. The logistic model for population growth. School of Mathematics etc. National University of Ireland, Galway. Ireland. [ Links ]

Stewart, J. 1996. Calculus: concepts and context. Brooks cole. Book 4th edition. 493 -508 pp. [ Links ]

Thornes, B. J. 2004. Stability and insestability in the management of Mediterranean desertification. In: Wainwright, J. and Mulligan, M. (Eds.). Environmental Modelling. Finding Simplicity in Complexity. John Wiley & Sons, Ltd. 303-315 p. [ Links ]

Van der Knijff J. M.; Jones R. J. A. and Montanarella, L. 2000. Soil erosion assessment risk in Europe. European Commission Directorate General Jrc Joint Research Centre Space Applications Institute European Soil Bureau. 31 p. [ Links ]

Wainwright, J. and Mulligan, M. 2004. Environmental modelling. Finding simplicity in complexity. John Wiley & Sons, Ltd. London. 822 p. [ Links ]

Wolfram, S. 2002. A new kind of science. Champaign, IL. Wolfram Media. 918 p. [ Links ]

Received: May 2018; Accepted: June 2018

§Corresponding author: apedroza@chapingo.uruza.edu.mx.

Creative Commons License Este es un artículo publicado en acceso abierto bajo una licencia Creative Commons

 
Campo Experimental Valle de México, Km13.5, Carretera Los Reyes-Lechería, Colonia Coatlinchán, Texcoco, Estado de México, MX, 56250, (52-595) 92 12681