Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ciencias agrícolas
versão impressa ISSN 2007-0934
Rev. Mex. Cienc. Agríc vol.7 no.8 Texcoco Nov./Dez. 2016
Articles
Grain yield stability in trilinear male sterile corn hybrids for Valles Altos de Mexico
1Colegio de Postgraduados- Campus Montecillo. CP. 56230. Montecillo, Texcoco, Estado de México. Tel. 01 (595) 952-0257. Fax: 01 (595) 952-0262. (enrique1784@yahoo.com.mx; mapolina@colpos.mx; zavala@colpos.mx; fcastill@colpos.mx).
2Universidad Nacional Autónoma de México- FES Cuautitlán. (tadeorobledo@yahoo.com).
3INIFAP-C. E. Valle de México, C. E. Cotaxtla y C. E. Iguala. (espinoale@yahoo.com.mx; mauro_s55@hotmail.com; noelorlando19@hotmail.com).
At the Facultad de Estudios Superiores Cuautitlán (FESCUNAM) and the Instituto Nacional de Investigaciones Forestales, Agricolas y Pecuarias (INIFAP-CEVAMEX), has trilinear maize hybrid (Zea mays L.), whose single crosses parent possess male sterility to facilitate seed production, maintain their genetic quality and reduce seed production costs. Prior to commercial release of the hybrids for its extensive use, it is required to identify the best genotypes, based on yield and stability under different environments. The aim of this study was to identify trilinear corn hybrids grain yield stability, using Eberhart and Russell stability parameters and the additive main effect and multiplicative interaction (AMMI) model, thus to define the model that best describes the interaction genotype per environment. Four sterile and fertile male trilinear hybrids were evaluated in experiments established with one irrigatio in two locations in springsummer 2012, and in each of two planting dates and two population densities, eight test environments, combining locality x planting date x population densities were formed. AMMI identified as stable the trilinear hybrids H-57 and Puma 1183 AEC2, while the stability parameters model identified hybrids H-53, Puma 1183 AEC1 and Puma 1183 AEC2 as stable for their regression coefficients close to unit and regression of deviations close to zero. The levels of correspondence between the two models were 50% for hybrids. It is concluded that both models identified at least a trilinear hybrid as stable, but it was the AMMI model that best described the interaction genotype x environment.
Keywords: Zea mays; adaptability; male sterility; productivity; seed production; single crosses; stability; yield
En la Facultad de Estudios Superiores Cuautitlán (FESCUNAM) y el Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (INIFAP-CEVAMEX), se cuenta con híbridos trilineales de maíz (Zea mays L.), cuyas cruzas simples progenitoras poseen androesterilidad para facilitar la producción de semillas, mantener su calidad genética y para disminuir costos de producción de semilla. Previo a la liberación comercial de los híbridos para su uso extensivo, se requiere identificar los mejores genotipos, con base en rendimiento y estabilidad en diferentes ambientes de prueba. El objetivo de este trabajo fue identificar híbridos trilineales de maíz que presenten estabilidad del rendimiento de grano, utilizando los parámetros de estabilidad de Eberhart y Russell y el modelo de interacción multiplicativo y de efectos principales aditivos (AMMI, por sus siglas en inglés), así como definir el modelo que mejor describa la interacción genotipo por ambiente. Se evaluaron cuatro híbridos trilineales androestériles y fértiles en experimentos establecidos en condiciones de punta de riego, en dos localidades en el ciclo primavera- verano 2012, y en cada una de dos fechas de siembra y dos densidades de población. Se conformaron ocho diferentes ambientes de prueba, combinando localidades x fechas de siembra x densidades de población. El modelo AMMI identificó como estables a los híbridos trilineales H-57 y Puma 1183 AEC2, mientras que el modelo de parámetros de estabilidad identificó a los híbridos H-53, Puma 1183 AEC1, y Puma 1183 AEC2 como estables por sus coeficientes de regresión cercanos a la unidad y desviaciones de regresión próximas a cero. Los niveles de correspondencia entre ambos modelos fueron de 50% para los híbridos. Se concluye que ambos modelos identificaron por lo menos a un híbrido trilineal como estable, pero fue el modelo AMMI el que mejor describió la interacción genotipo por ambiente.
Palabras clave: Zea mays; adaptabilidad; androesterilidad; cruzas simples; estabilidad; productividad; rendimiento; producción de semillas
Introduction
The use of trilinear corn hybrid (Zea mays) in Mexico, including Valles Altos (2 200-2 600 masl), is widespread nowadays; its beginning dates back to 1986, when identifying advantages to this type of hybrids: facilitate seed production; fewer parents are required to reach the production of certified seed; control of genetic quality is accessible as it is easy to demix the male parent line, thus Rowe and Andrew (1964) overall mention that homogeneous maize populations (inbred lines and single crosses) show lower stability than heterogeneous populations (double and trilinear crosses).
In the period 1943-1985, double cross hybrids from low inbreeding parents, was the formation of hybrid most commonly used in Mexico, based on an objective related to the intent that this had greater adaptability; however, overall showed low heterosis, difficulty for seed production, more effort for its production in crop cycles, and higher production costs to obtain final hybrid (Espinosa et al., 1986). The single cross hybrids that have been generated for the production area Valles Altos have not had the expected production potential, but neither has highly yielding lines homozygous females; these hybrids have high genotype*environment interaction (GE). These simple crosses are the key to obtaining trilinear hybrid, because the single cross that participates as female has high productivity (Espinosa et al., 1998; Sierra et al., 2006; Márquez, 2009).
In breeding programs, it is important to define which genotypes are outstanding in yield, adaptation and stability, assessing these properties in multi-environments to recommend its use commercially (Crossa et al., 2006). Adaptation broadly refers to the outperformance of a genotype in most test environments, while is specific aspects, the sample genotype with outperformance in a given test environment (Cooper et al., 1999; Fuentes et al., 2005). In this regard, Hanson (1970) defines stable genotype as that having the lowest possible variability, when grown under different environments.
The study of genotype*environment (GE) interaction in plant breeding is very important because this is the response of each genotype against environmental variations (Crossa et al., 2006). To make further progress in genetic breeding of a species, it is necessary to properly establish the methodologies to be used for the evaluation of the genotype*environment (GE) interaction, to accurately estimate the differential response of genotypes across test environments.
Among the various methodologies for the study of crop stability, highlights the Eberhart and Russell (1966) model, modified from Finlay and Wilkinson (1963) method, using the arithmetic mean of actual data and noting that the regression coefficient from environmental effects on phenotypic effects can be used as an estimator to measure the response of each cultivar to environmental indices, and production stability is possible to measure the magnitude of deviation from the linear regression; that is, by the mean square deviation of regression. In this model a variety with high average, regression coefficient ßi = 1 and deviation not significantly different from zero (
Moreover, in multivariate methods, the additive main effect and multiplicative interaction model (AMMI), consists essentially of combining the techniques of analysis of variance and principal component analysis (PCA) in a single model, here the analysis of variance allows to study the main effects of genotypes and environments, while the genotype x environment interaction (IGA) is treated in a multivariate way by the ACP, where a reconfiguration of the regression model is performed to improve the interpretation of the interaction (Zobel , 1988).
To interpret the results obtained from AMMI analysis, according to Yan et al. (2000), it is to use the combined effects of genotypes (G) and the interaction genotype x environment (IGE) in yield evaluation, obtaining the graphics called GGE biplot (genotype G + genotype*environment interaction GE), which facilitate visual identification of genotypes and environment evaluation. Generally, GGE biplot graphics are made using the first two principal components (CP1 and CP2). Thus, the genotype that is at the vertex is the one that responds better in environments of evaluation (Yan et al., 2001).
Based on the above, the objective of this study was to identify trilinear corn hybrids that have better grain yield stability, using two models to assess the stability parameters stability from Eberhart and Russell and AMMI, thus define the model that best describe the genotype*environment interaction. Based on the results, it is intended to recommend the subsequent commercial release in the case of the best trilinear hybrids identified in this work.
Materials and methods
This work was carried out in the spring-summer 2012, in two locations; the first was FESC-UNAM (Cuautitlán-UNAM), municipality of Cuautitlan Izcalli, State of Mexico, at an altitude of 2 274 m; the second location was on the field Santa Lucia de Prías from the Campo Experimental Valle de Mexico (CEVAMEX), from the Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (INIFAP), municipality of Texcoco, State of Mexico, at an altitude of 2 240 masl. In both locations, two experiments were planted in two sowing dates. In Cuautitlán-UNAM the first planting date was May 21, 2012 and second on June 1, 2012, while in CEVAMEX-INIFAP, the first planting date was May 18, 2012 and the second May 29, 2012.
Trilinear hybrid Puma 1183 AEC1 and Puma 1183 AEC2 from UNAM, H-53 (Espinosa et al., 2012a) and H-57 (Espinosa et al., 2012b) from INIFAP were used, all in their male-sterile version (AE) and fertile (F) in two population densities, 55 000 and 70 000 plants per hectare; densities that are recommended by the phenotypic characteristics of plants genotypes evaluated by competition. Trilinear hybrids the two planting dates and the two population densities in the two locations were individualized to form environments, thus creating eight environments (two locations x two sowing dates x two population densities).
In all environments, at different planting date, irrigation was applied after planting. For weed control Gesaprim (atrazine) was used at a dose of 2 kg ha-1 and Hierbamina (24D amine) at a dose of 2 L ha-1. The harvest was performed on December 10 and 17, 2012 in Cuautitlan Izcalli and Santa Lucia respectively. In both localities a complete randomized block design with three replications was used, where the experimental plot was a groove of 5 m long and 0.80 m between rows, the useful plot had an area of 4 m2. A factorial design for statistical analysis of yield, where variation factors for trilinear hybrids were environments, genotypes and interactions between variation factors was used; comparison of means was performed with Tukey at 0.05; to assess genotype*environment interactions, the variable yield from trilinear hybrids was used as variable.
To evaluate the response of environments, genotypes and IGA the additive main effects and multiplicative interaction (AMMI) was used, an analysis of variance was performed to determine the effects of genotypes, environments, and their interactions. The first two principal components were considered to explain genotype*environment interaction. Graph representations were obtained by a Biplot, which showed the pattern of genotypes*environments interaction.
For the analysis AMMI programming routines described by Vargas and Crossa (2000) were employed, using the following mathematical model:
Where: Yij= yield of the ith genotype in the jth environment; μ= general mean; gi= effect of the ith genotype; ej= effect of the j-th environment; λk= square root of the characteristic vector from the kth axis of ACP; αik= ACP scoring for the kth axis of the ith genotype; γjk= ACP scoring for the kth axis from the jth environment; Eij= value of the error.
Eberhart and Russell (1966) stability parameter were obtained to measure the genotype x environment interaction, and the classification of varieties adaptability proposed by Carballo and Márquez (1970) was used, where bi is the regression coefficient and
Where: Yij= average from genotype i in the j environment; μi= average from genotype i in all environments; βi= regression coefficient that measures the response from genotype i in varying environments; Ij = environmental index of the jth environment, which is calculated as the deviation from genotype average in a given environment from the overall average; δij= deviation of regression.
The data used in this methodology were analyzed by applying a computational algorithm to obtain stability indicators from Mastache and Martínez (1996).
All statistical analyzes were performed using SAS version 9.0 (SAS Institute, 2002).
Results and discussion
The combined analysis of variance from AMMI (Table 1) detected highly significant differences between environments and between genotypes for yield, while for genotype*environment interaction was not significant. The coefficient of variation was 12.7%, considered an acceptable value as to the condition of the experiment, for the values obtained by r-square and application of the experimental design. The difference between environments for yield indicates that environmental conditions and their effects on genotypes were different in all test environments. The difference in yield between genotypes was the result of genetic divergence among hybrids evaluated, i.e., the yield from genotypes was not the same because these had a different genetic origin, because the progenitors were derived from different maize populations. The absence of significance of genotype x environment interactions (IGE) for yield, which is a highly quantitative trait and therefore greatly influenced by environmental conditions, indicates that statistically there was not a differential response from genotypes yield through the different test environments.
Table 1 Analysis of variance AMMI for yield of four hybrids evaluated in eight environments FESC-UNAM and Santa Lucía INIFAP, spring - summer 2012.
| Fuente de Variación | G.L | SC | CM |
| Ambientes (a) | 7 | 18081507.04 | 2583072.43 ** |
| Genotipos (g) | 3 | 54167006.91 | 18055668.97 ** |
| Interacción (gxa) | 21 | 14316864.75 | 681755.5 |
| CP1 | 9 | 8885107.4 | 987234.15 |
| CP2 | 7 | 3944506.8 | 563500.97 |
| Error | 62 | 39381766.9 | 635189.8 |
| Total Corregido | 95 | 127620558 | |
| CV (%) | 12.7 | ||
| Promedio | 6293.4 |
*, **: Significancia (p≤ 0.05, 0.01); GL= grados de libertad; SC= suma de cuadrados; CM= cuadrados medios; CV= coeficiente de variación; CP1 y CP2= componente principal.
Regarding the amount of the total sum of squares, the effect of environments contributed 14.2%, the genotypes x environments interaction in 11.2%, and 42.4% of the total corresponded to genotypes effect. This indicates that the genotypes, as a whole, contributed in higher proportion to yield variation compared to environmental factors and genotype*environment interaction, even when there were highly significant differences between environments. This result contrasts with that obtained in other researches, in which the environmental factor and genotype*environment interaction were higher than the genotypes effect (Alejos et al., 2006 Palemón et al., 2012).
The genotypes that had the highest yield were H-53 and H-57 in all test environments. Environments with higher yields were Cuautitlán in the second planting date (June 1, 2012), with a population density of 50 000 plants per hectare and Cuautitlán in the second planting date (June 1, 2012), with a population density 70 000 plants per hectare; as result of beneficial environmental conditions in the locality of Cuautitlán, of rainfall and soil properties to retain available moisture for the plant. Genotypes that scored lower absolute values from CP1, i.e., that interacted less with the environment, were, H-57, with 14.72, and Puma 1183 AEC2 with -17.93, when presenting the values of CP1 closer to zero, were considered the most stable across environments (Medina et al., 2002; Alejos et al., 2006; Palemón et al., 2012).
Environments with better yield (we cannot say that an environment is stable, it is wrong therefore it is added to have good behavior) with respect to absolute values of CP1 were: Cuautitlán in the second planting date, with population density of 70 000 plants per hectare (A5), with -0.28; Santa Lucia in the first planting date, with a population density of 50 000 plants per hectare (A3), with 5.12; Santa Lucia in the second planting date, with population density of plants per hectare (A7), with 9.15, and Cuautitlán in the first planting date, with population density of plants per hectare (A2), with -9.3 (Table 2).
Table 2 Average yield in kg ha-1 of four maize genotypes evaluated in eight environments and the two first values of principal components for genotypes and environments. FESC-UNAM and Santa Lucía INIFAP, spring - summer 2012.
| Genotipo | Ambiente | Media (kg ha-1) | CP1 | CP1 | |||||||
| Cuautitlán | Cuautitlán | Santa Lucía | Santa Lucía | Cuautitlán | Cuautitlán | Santa Lucía | Santa Lucía | ||||
| F1 D1 | F1 D2 | F1 D1 | F1 D2 | F2 D1 | F2 D2 | F2 D1 | F2 D2 | ||||
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | ||||
| Puma 1183 | 5624.5 | 5709.6 | 4880 | 4723.9 | 6007.6 | 5859.7 | 5147.4 | 5090.3 | 5380.4 | -22.66 | -16.4 |
| AEC1 | |||||||||||
| Puma 1183 | 5793.5 | 6384.4 | 5146.2 | 5698.1 | 6372.3 | 7543.1 | 5727.8 | 6191.4 | 6107.1 | -17.93 | 12.9 |
| AEC2 | |||||||||||
| H-53 | 6128.9 | 7409.4 | 7180.9 | 7714.6 | 7634.2 | 7507.4 | 7775.3 | 8156.6 | 7469.6 | 25.87 | -17.03 |
| H-57 | 5118.6 | 6091.8 | 5391 | 6785.5 | 6737.8 | 7356.2 | 5937.4 | 6313.9 | 6216.5 | 14.72 | 20.5 |
| Media (kg ha-1) | 5728.7 | 6398.8 | 5649.5 | 6230.5 | 6766.1 | 6971.35 | 6147 | 6438.1 | |||
| CP1 | -25.8 | -9.3 | 5.12 | 21.4 | -0.28 | -14.3 | 9.15 | 14.02 | |||
| CP2 | -10.6 | -3.1 | -14.3 | 11.1 | 8.8 | 22.2 | -10.64 | -3.52 | |||
Hybrid H-53 showed a higher average yield than average,while the other three hybrids had lower yields than average (Figure 1). Puma 1183 AEC1 showed the lowest average yield. Hybrids with low values i n CP1 and that interacted less with the environment were, H-57 and Puma 1183 AEC2, while genotypes with greater interaction with the environment for its CP1 high values were, H-53 and Puma AEC1. More precisely, it was possible to identify environments A5, A3, A7 and A2 as those with the best behavior, for its yield and CP1 values, for being closer to zero, i.e., those that showed the least variation between them, and considering that each environment influenced population density, locality and planting date on environments A5, A3, A7 and A2 having the best conditions for the best yields.
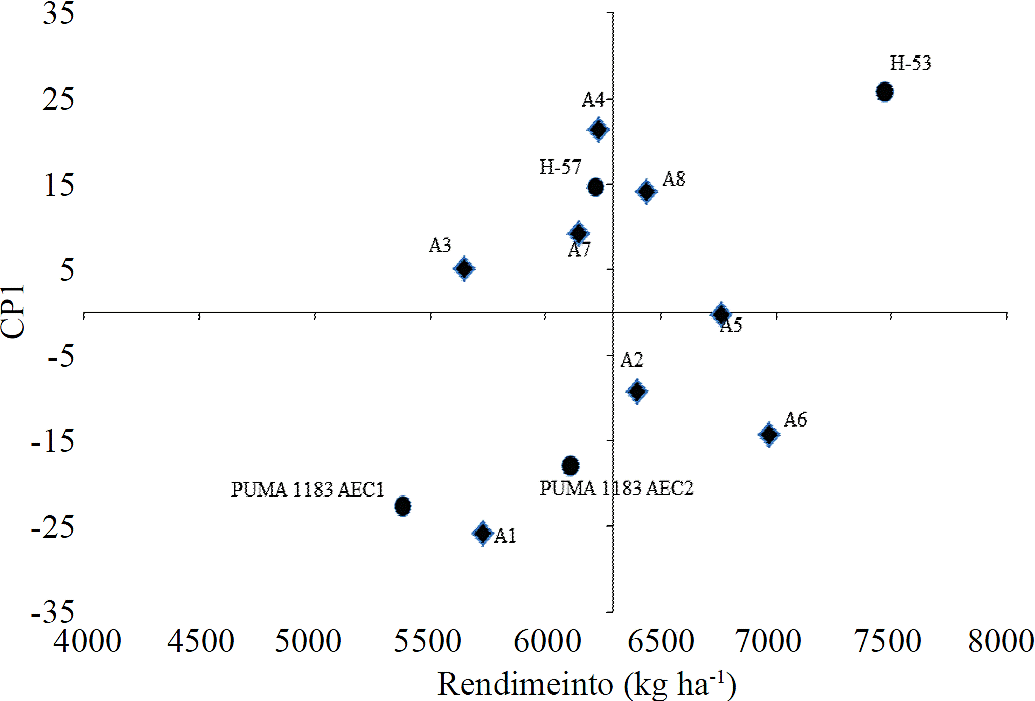
The circles represent the genotypes and diamonds environments.
Figure 1 CP1 biplot based on the average yield of four trilinear maize hybrids evaluated in eight environments in the FESC-UNAM and Santa Lucía INIFAP, spring - summer 2012.
In the AMMI analysis, the first principal component (PC1) explained 60.5% sum of squares, and the second principal component (PC2) observed 26.8% of the sum of squares, so between the two main components described 87.3% the effect of genotype x environment interaction. Furthermore, with respect to environments, Yan et al., (2000) point out that the environments whose angles are less than 90 ° will classify the genotypes in the same manner. In this case, in particular two environments groups with similar behaviors were formed; in the first group environments, A1, A2, A5 and A6 were found; in the second A3, A4, A7 and A8, being environments A1, A4 and A6, those that best discriminated genotypes.
Meanwhile, Eeuwijk (2006) indicates that a smaller angle of 90° or greater than 270° between crop vector and site vector indicate that the cultivar has a positive response to the test site. A negative response of the cultivar is indicated with angles greater than 90° and below 270°. This coincides with the results from biplot (Figure 2), where H-53 responded better in the A7, A8, A3 and A4 environments, while H-57 showed a better response in the A4, A8 and A6 environments. Meanwhile, Puma 1183 AEC2 improved in the A5, A6 and A2 environments, while Puma 1183 AEC1 showed a better response in A5, A2 and A1. Thus, the genotypes closest to the origin in the biplot were the least interacting with the environment and therefore the most stable; on the contrary, the farthest showed greater variation in their behavior (Yan et al., 2000). These results show that the most stable genotypes were Puma AEC2 1183 and H-57, while genotypes that most interacted with the environment were H-53 and Puma 1183 AEC1.
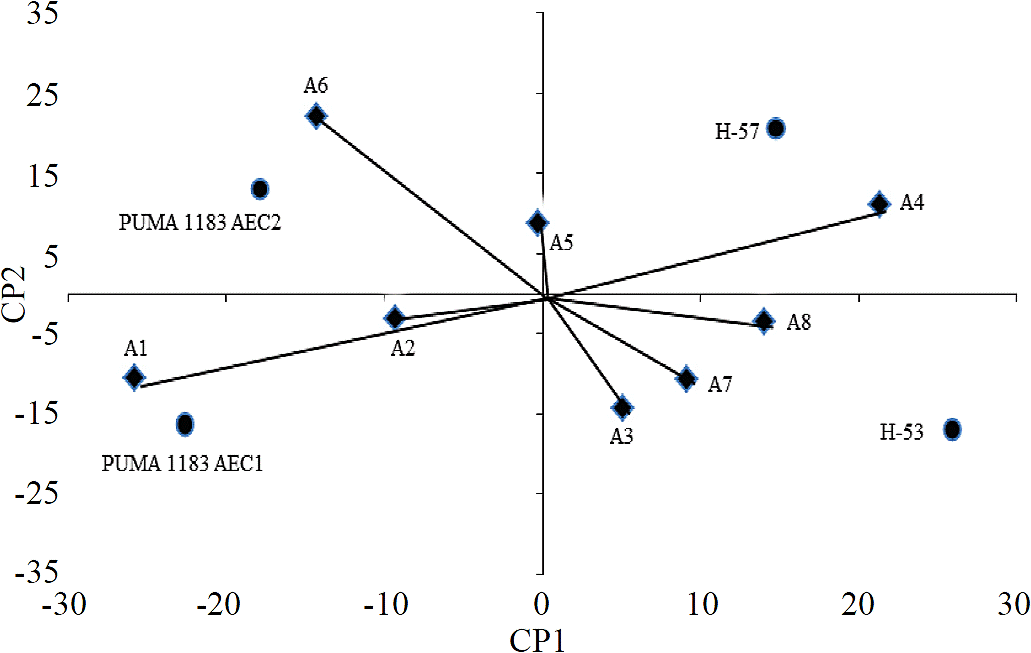
Figure 2 AMMI biplot for four trilinear maize hybrids; the points represent the trilinear hybrids and vectors represent environments.
The analysis of variance of Eberhart and Russell (1966) stability parameters, for yield, showed no significance between environments, genotypes, and genotype*environment interaction. This indicates that between environments, environmental conditions had similar behavior, which caused no significant effect on yield, whereas for genotypes, even though came from different genetic origin, their average behavior in all environments was very similar. The genotype*environment interaction, not being significant indicates that there was a differential response of genotypes yield across different test environments.
According to estimated stability parameters, the regression coefficient (bi), deviation of regression (
Table 3 Average yield, regression coefficient (bi), deviations regression (
| Genotipo | Rendimiento (kg ha-1) | bi |
|
| PUMA 1183 AEC1 | 5380 | 0.5286 | -213063.97 |
| PUMA 1183 AEC2 | 6107 | 1.3304 | -292066.93 |
| H-53 | 7438 | 0.7117 | -121018.54 |
| H-57 | 6217 | 1.4293 | -309803.83 |
*, **= significancia (p≤ 0.05, 0.01); SC= suma de cuadrados; CM= cuadrados medios; CV= coeficiente de variación.
To define the best methodology to characterize the most stable genotypes and environments where genotypes have better yield response, for this, the values of the first principal component (PC1) corresponding to AMMI methodology and the environmental indices values for the methodology of stability parameters were compared. Table 4 shows that AMMI model identified as environments with better response from genotypes for yield to A5, A3, A7 and A2, for having CP1 values closer to zero, while the environments with poor response of genotypes in yield were, A1, A4, A6 and A8, for having CP1 values farthest from zero. The stability parameters model identified as the best environments for yield to A6, A5, A8 and A2, by the values of its positive environmental indices; i.e., higher than the overall average, and environments with bad behavior were, A1, A3, A7 and A4, for having negative environmental indices; i.e., lower than overall average. The correspondence between the two models was 50%, since both models coincide in determining two stable and two unstable environments, from the eight test environments.
Table 4 Average behavior of yield in the eight environments evaluated, principal component one (CP1) and environmental indices; FESC UNAM and Santa Lucía INIFAP, spring - summer 2012.
| Ambientes | Rendimiento (kg ha-1) | CP1 | Índice ambiental |
| A1 | 5728 | -25.8 | -619.4 |
| A2 | 6399 | -9.3 | 113.2 |
| A3 | 5649 | 5.1 | -636.1 |
| A4 | 6230 | 21.4 | -55.1 |
| A5 | 6766 | -0.28 | 402.4 |
| A6 | 6971 | -14.3 | 781 |
| A7 | 6147 | 9.1 | -138.6 |
| A8 | 6438 | 14 | 152.5 |
*, **= significancia (p≤ 0.05, 0.01); GL= grados de libertad; SC= suma de cuadrados; CM= cuadrados medios; CV= coeficiente de variación; CP1 y CP2= componente principal.
Comparing AMMI with Eberhart and Russell model to identify the most stable genotypes (Table 5), with the AMMI model the most stable genotypes were H-57 and Puma 1183 AEC2, for their CP1 values closest to zero; with the stability parameters model, all genotypes were stable. The correspondence between both models was 50%, since only two of the four genotypes evaluated match as stable with both models, similar results to those from Cordova (1991), who obtained 40% match when using both methodologies.
Table 5 Yield response of four hybrids evaluated, principal component one (CP1) and regression coefficient. FESC-UNAM and Santa Lucía INIFAP, spring - summer 2012.
| Genotipo | Rendimiento (kg ha-1) | CP1 | bi |
| PUMA 1183 AEC1 | 5380 | -22.7 | 0.5286 |
| PUMA 1183 AEC2 | 6107 | -17.9 | 1.3304 |
| H-53 | 7438 | 25.9 | 0.7117 |
| H-57 | 6217 | 14.7 | 1.4293 |
*, **= significancia (p≤ 0.05, 0.01); GL= grados de libertad; SC= suma de cuadrados; CM= cuadrados medios; CV= coeficiente de variación; CP1 y CP2= componente principal.
Conclusions
Trilinear hybrids H-57 and Puma 1183 AEC2 had the best stability and higher yield. Environments with best genotypes behavior in yield of trilinear hybrids were, Cuautitlán in the second planting date, planting density of 50 000 plants per hectare (A5); Santa Lucía in the first planting date, planting density of 50 000 plants per hectare (A3); Santa Lucía on the second date of planting with planting density of 50 000 plants per hectare (A7) and Cuautitlán in the first planting date, with planting density of 70 000 plants per hectare (A2).
The best model to analyze the genotype*environment interaction was AMMI, compared with the stability parameters of Eberhart and Russell. This is because the interaction genotype*environment should be analyzed as a multiplicative effect and not just as a linear effect, in addition to the use of Biplot, is easily explained genotype*environment interaction, using the values of the principal components and genotypes yield.
Literatura citada
Alejos, G.; Monasterio, P. y Rea, R. 2006. Análisis de la interacción genotipoambiente para el rendimiento de maíz en la región maicera del estado de Yaracuy, Venezuela. Agron. Trop. 56(3):369-384. [ Links ]
Carballo, C. A. y Márquez, S. F. 1970. Comparación de variedades de maíz de El bajío y la mesa central por su rendimiento y estabilidad. Agrociencia. UACH. México, D. F, 129-146 pp. [ Links ]
Cooper, M. P. 1999. Genotipe x environment interactions, selection response and heterosis. In: Coors, J. G. y Pandey, S. (Eds.). The genetics and explotation of heterosis In: Crops. Crop science society of America. CIMMYT. Madison, Wisconsin, USA. 81-92 pp. [ Links ]
Córdova, O. H. S. 1991. Estimación de parámetros de estabilidad para determinar la respuesta de híbridos de maíz (Zea mays L.) a ambientes contrastantes de Centroamérica, Panamá y México. Agron. Mesoam. 2. 1-10. [ Links ]
Crossa, J.; Burgueño, J.; Cornelius, P. L.; Mclaren, G.; Trethowan, R. and Krishnamachari, A. 2006. Modeling genotype x environment interaction using additive genetic covariances of relatives for predicting breeding values of wheat genotypes. Crop Sci. 46:1722- 1733. [ Links ]
Crossa, J.; Gauch, H. G. and Zobel, R. 1990. Additive main effect and multiplicative interaction analysis of two international maize cultivar trials. Crop Sci. 30:493-500. [ Links ]
Crossa, J. y Cornelius, P. L. 2000. Modelos lineales bilineales para el análisis de ensayos de genotipos en ambientes múltiples. In: Simposium: Interacción genotipo x ambiente. XIII Congreso Nacional de Fitogenética. Sociedad Mexicana de Fitogenética A. C. 15-20 de octubre. Irapuato, México. 61-88 pp. [ Links ]
Eberhart, S. and Russell, A. W. 1966. Stability parameters for comparing varieties. Crop Sci. 6:36-40. [ Links ]
Eeuwijk, F. V. 2006. Genotype by environment interaction. Basics and beyond. In: Lamkey, K. R. and Lee, M. (Eds.). Plant breeding: the Arnel H. International Symposium. México. 155-170 pp. [ Links ]
Espinosa, C. A. y Carballo C., A. 1986. Productividad y calidad de semillas en líneas e híbridos de maíz (Zea mays L.) para la zona de transición de México. Fitotecnia 8:1-25. [ Links ]
Espinosa, C. A.; Ortíz, C.; Ramírez, F. J.; Gómez, M. N. O. y Martínez, G. A. 1998. Estabilidad y comportamiento de líneas per se y cruzas de maíz en la producción de semilla. Agric. Téc. Méx. 24(1):27-36. [ Links ]
Espinosa, C. A.; Tadeo, R. M.; Gómez, M. N.; Virgen, V. J.; Sierra, M. M.; Palafox, C. A.; Zamudio, G. B.; Arteaga, E. I.; Canales, I. E. I.; Martínez, Y. B.; Vázquez, C. G. y Valdivia, B. R. 2012 a. H-53 AE1: híbrido de maíz para Valles Altos y Zona de Transición con esterilidad masculina para producción de semilla. CEVAMEX. Memoria técnica Núm. 13. 38-40 pp. [ Links ]
Espinosa, C. A.; Tadeo, R. M.; Gómez, M. N.; Virgen, V. J.; Sierra, M. M.; Palafox, C. A.; Zamudio, G. B.; Arteaga, E. I.; Canales, I. E. I.; Martínez, Y. B.; Vázquez, C. G. y Valdivia, B. R. 2012 b. H-57 AE: híbrido de maíz para valles altos con esterilidad masculina para producción de semilla. Campo Experimental Valle de México. Memorias de congresos. Memoria Técnica núm. 13. 41-44 pp. [ Links ]
Finlay, K. W. and Wilkinson, G. N. 1963. The analysis of adaptation in plant breeding programme. Austr. J. Agric. Res. 14: 742-754. [ Links ]
Fuentes, L. M. y Quemé, W. R. 2005. Evaluación de híbridos de maíz de gano amarillo y blanco en diferentes ambientes de México y Centro América. Informe del PCCMA Guatemala. abril 2005. [ Links ]
Gauch, H. G. 1992. Statistical analysis of regional yield trials: AMMI analysis of factorial designs. Elsevier Science Publishers, USA. 278 p. [ Links ]
Hanson, W. D. 1970. Genotypic stability. Theor. Appl. Gen. 40:D6-231. [ Links ]
Márquez, S. F. 2009. De las variedades criollas de maíz a los híbridos transgénicos. II. La hibridación. Agric. Soc. Des. 6(2):161-176. [ Links ]
Márquez, S. F. 1973. Relationship between genotipe-environment interaction and stability parameters. Crop Sci. 13:577-579. [ Links ]
Mastache, L. A. y Martínez, G. A. 1996. Un algoritmo computacional para obtener los indicadores de estabilidad de Eberhart y Russell. Comunicaciones en Estadística y Cómputo. Colegio de Postgraduados. México. 22 p. [ Links ]
Medina, S. C.; Marín, V.; Segovia, A.; Bejarano, Z.; Venero, R. A. y Meléndez, E. 2002. Evaluación de la estabilidad del rendimiento de variedades de maíz en siete localidades de Venezuela. Agron. Trop. 52(3):255-275. [ Links ]
Mejía, C. J. A. y Molina, G. J. D. 2003. Cambios de estabilidad en el rendimiento de variedades tropicales de maíz. Rev. Fitotec. Mex. 26(2):89-94. [ Links ]
Palemón, A. F.; Gómez, M. N. O.; Castillo, G., F.; Ramírez, V. P.; Molina, G.; J. D. y Miranda, C. S. 2012. Estabilidad de cruzas intervarietales de maíz (Zea mays L.) para la región semicálida de Guerrero. Agrociencia. 46. 133-145. [ Links ]
Rodríguez, P. J. E.; Sahagún, C. J.; Villaseñor, M. H. E.; Molina, G. J. D. y Martínez, G. A. 2002. Estabilidad de siete variedades comerciales de trigo (Triticum aestivum L.) de temporal. Rev. Fitotec. Mex. 25(2):143-151. [ Links ]
Rowe, P. R. and Andrew, R. 1964. Phenotipic stability for a systematic series of corn genotypes. Crop Sci. 4:563-567 [ Links ]
SAS. 2002. The SAS System for Windows. SAS Institute Inc. Cary, NC 27513, USA. [ Links ]
Sierra, M. M.; Palafox, C. A.; Rodríguez, M. F. A.; Espinosa, C. A.; Gómez, M. N.; Caballero, H. F.; Barrón, F. S.; Sandoval, R. A. y Vázquez, C. G. 2006. H-518, híbrido trilineal de maíz para el trópico húmedo de México. Agric. Téc. Méx. 32(1):115-119. [ Links ]
Vargas, M. and Crossa, J. 2000. The AMMI analysis and graphing the Biplot. Biometrics and statistical unit. CIMMYT. México. 42 p. [ Links ]
Yan, W.; Hunt, L. A.; Sheng, Q. and Szlavnics, Z. 2000. Cultivar evaluation and mega-environment investigation based on GGE biplot. Crop Sci. 40:597-605. [ Links ]
Yan, W. 2001. GGE-biplot- a windows application for graphical analysis of multi-environment trial data and other types of two-way data. Agron. J. 93:1111-1118. [ Links ]
Zobel, R. W.; Wright, M. and Gauch, H. G. 1998. Statistical analysis of a yield trial. Agron. J. 80:88-397. [ Links ]
Received: June 2016; Accepted: September 2016











 texto em
texto em 


