Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ciencias agrícolas
versão impressa ISSN 2007-0934
Rev. Mex. Cienc. Agríc vol.7 no.4 Texcoco Mai./Jun. 2016
Articles
Mathematical modeling system of the fruit-pedicel-peduncle Manila mango
1 Departamento de Ingeniería Mecánica Agrícola- Universidad Autónoma Chapingo. Carretera México-Texcoco, km 38.5, Texcoco, México. C. P. 56230. Tel: 5959521680. (alelopez10@hotmail.com; eugenior@correo.chapingo.mx; sobrevill2002@hotmail.com).
The mango cultivation in Mexico represents an important source of jobs, income and foreign exchange, only in 2002 entered the country 134 million dollars to export 195 thousand tons of mango. Mexico contributes to world exports 30% of total production, which places it as the largest exporter in the world; however, the harvest is done manually. This study aims to determine the most appropriate vibration systems for selective detachment of the fruits using a model of two degrees of freedom. The input data for the evaluation of this model were the physical-mechanical fruit-pedicel- peduncle system properties. As a result of modeling the frequency responses for linear movement, rotation angle, bending moment and tensile strength in the three stages of maturation observed separation between the resonance frequencies of green and ripe fruits they were obtained, which is a fortress for the selective harvesting of fruits. The frequency bands in which only the fall of the ripe fruits for different amplitudes produced were also obtained. For the first mode of vibration it is sufficient with an amplitude of 10 mm excitation to release only the ripe fruit in a band of 14.3 Hz (27.5-41.8 Hz); green fruit would divest from a frequency of 56 Hz demonstrating the possibility of selective harvesting the fruits of the handle.
Keywords: modeling; resonance frequency; selectivity and excitation amplitude
El cultivo del mango en México representa una fuente importante de empleos, ingresos y generación de divisas, sólo en el año 2002 ingresó al país 134 millones de dólares al exportar 195 mil toneladas de mango. México aporta a las exportaciones mundiales el 30% del total de la producción, lo que lo sitúa como el mayor exportador del mundo; sin embargo, su cosecha se realiza de forma manual. El presente trabajo tiene como objetivo determinar los regímenes de vibración más apropiados para el desprendimiento selectivo de los frutos empleando un modelo de dos grados de libertad. Los datos de entrada para la evaluación de este modelo fueron las propiedades físico-mecánicas del sistema fruto-pedicelo-pedúnculo. Como resultado de la modelación se obtuvieron las respuestas de frecuencia para el desplazamiento lineal, ángulo de giro, momento f lector y la fuerza traccional en los tres estadios de maduración, observándose separación entre las frecuencias de resonancia de los frutos verdes y maduros, lo que constituye una fortaleza para la cosecha selectiva de los frutos. También se obtuvieron las bandas de frecuencia en la que sólo se produce la caída de los frutos maduros para diferentes amplitudes. Para el primer modo de vibración es suficiente con una amplitud de excitación de 10 mm para desprender solamente los frutos maduros en una banda de 14.3 Hz (27.5-41.8 Hz); los frutos verdes se desprenderían a partir de una frecuencia de 56 Hz lo que demuestra la posibilidad de la cosecha selectiva de los frutos del mango.
Palabras clave: frecuencia de resonancia; modelación; selectividad y amplitud de excitación
Introduction
The modeling of the fruit-stem system has been a tool used during investigations related to mechanical harvesting of fruits by vibration from the decade of the sixties (Fridley and Adrian, 1960; Rumsey, 1967; Cooke and Rand, 1969; Varlamov, 1972; Bobeva, 1972). The analysis of the dynamics of the fruit-peduncle system designed to determine the frequency response of the system when subjected to harmonic excitation has been subject to different modeling.
Classic models can be divided into two groups: Those who considered the predominant cause detachment of the fruits the action of centrifugal forces of inertia (driven) in the possible areas of abscission (fruit-union peduncle; peduncle-union branches or other) and those who believe as the predominant cause detachment of the fruits of action when inertial forces that cause bending in the abscission zones.
The first group are associated in some of the models developed in Europe and the United States (Adrian and Fridley, 1965; Varlamov, 1972; Bobeva, 1972), during studies at harvest vibration of fruits such as apples, plums and others, while the second group are mainly associated models encountered during studies citrus harvest vibration in United States of America (Cooke and Rand, 1969); in Cuba (Martinez, 1977; Castillo, 1995) it was also applied this model in guava (Herrera, 1980) in coffee (Martinez, 1989).
In research conducted at the coffee harvest by vibrations it has been continued by Gaskins (2006), based on these mathematical models determined vibration modes and regimes overlooking the selective harvesting of coffee fruits.
Both the model Cooke and Rand and the Martinez and Castillo have two degrees of freedom and take into account rightly the appearance of deflections in areas abscission of the fruit, which had not been considered in previous models and describing more accurately the phenomenon of bond failure of the fruit by the stem during harvest vibration.
An advantage to applying the model of two degrees of freedom proposed by Martinez may be noted that unlike the model Cooke and Rand can not only determine the resonance frequencies of the fruit-stalk system, but also calculate the bending moments arising in the abscission zone, which allows to determine the amplitudes of the excitation that cause detachment of the fruits. In addition, this model has been validated in experimental studies during harvest vibration in orange by Martinez (1982), in grapefruit by Llanes (2000) and coffee for Gaskins (2006).
As for the Castillo model, although it enables the calculation of the bending moments and amplitude of the excitation, is also applicable to the case of vibrations in the vertical, typical foliage vibrators which are not covered under this investigation.
Materials and methods
Figure 1 is a representation of this model, in which from the approach of the dynamics equations for the free body of the fruit, as well as the equations of deformation of peduncle, considered as an elastic beam, is obtain the differential equations of motion, of which the frequency response of displacement δ(ω) in m, angle of rotation of the fruit θ(ω) in rad, and the bending moment M(ω) is derived in N m and the normal force N(ω) in N, in the junction zone of the fruit and peduncle (abscission zone):
Where: A in s-2, B in m, C in s-2, D in m-1 and are calculated as:
Where: α in m N-1, β in N-1, γ in N-1 m-1, are calculated as:
Where: m= mass of fruit (kg); r= polar radius of the fruit, (m); I= moment of inertia centroidal fruit (kg m2); pedicel LV1= length (m); lv = peduncle length (m); EI1= stiffness of the pedicel, (N m2); EI2= stiffness peduncle (N m2); A, B, C, D, α, β and γ= parameters depending on the physical-mechanical fruit-pedicel-peduncle system properties.
The model considered the elastic properties of pedicel and peduncle; which they are considered cylindrical and with the same rigidity; the mass of the pedicels is neglected and the mass and length of the stems. The system is considered linear and undamped.
To facilitate the evaluation of the model, the computer program was used in Mathcad language used in grapefruit by Llanes (2000) and coffee Gaskins (2006). During the evaluation of the models took into account the statistical distribution of the different physical-mechanical object of study, aimed at obtaining the excitation frequency bands required for selective harvesting handle properties.
Results and discussion
Frequency response of the displacement and the rotation angle of the fruits
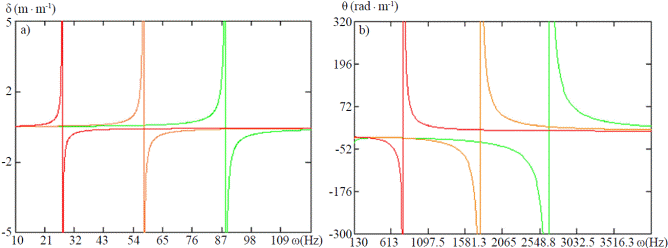
In Figure 2a and 2b, graphs of frequency response for a unit amplitude, linear displacement (δ) (Figure 2a) and the angle (θ) (Figure 2b) of ripe fruit (red lines) are shown and green fruits (green lines) corresponding to the Manila mango variety. In the graphs the presence of a first vibration mode whose resonance frequencies are in an environment of 26-81 Hz for linear movement shown, while for the angular displacement, the resonant frequency is in the range 774.8 to 2621 Hz.
Also, it is seen that in the environment thus the displacement of the fruits and rotation angle have the same sign, which is characteristic of a vibration mode in phase or pendular. Similarly, it is identified in the neighborhood of frequencies between 1581.3 to 2548.8 Hz a second mode of vibration in which the displacement of the fruits and rotation angle have opposite signs, which is characteristic of a vibration mode in antiphase.
It is noteworthy in this environment of frequencies, the appreciable gap between the resonance frequencies corresponding to ripe and unripe fruits; however, have the disadvantage of the high frequency values to generate by mechanical means, on the other hand curves frequency response of ripe and unripe fruit in the environment of the first vibration mode (pendular) are values relatively low which it is possible to achieve by mechanical means. As explained, this separation between the resonance frequencies of the systems and mature green fruit, is a strength in relation to the possibility of selective harvesting of fruits.
Frequency response of internal actions in the abscission zone
In Figures 3 and 4, comparing the effects shown in the detachment of the fruits of internal actions in the abscission zone, whether the bending moments or forces tractional; however, in practice it has been shown that the combination of both effects may occur when made detachment of the fruits. The horizontal lines represent the bending moment or tensile strength (mean values) respectively required for the release of the ripe fruits of the variety of mango Manila.

Figure 3 Frequency response bending moment in the abscission zone and tensile strength to an amplitude of the excitation of 20 mm.
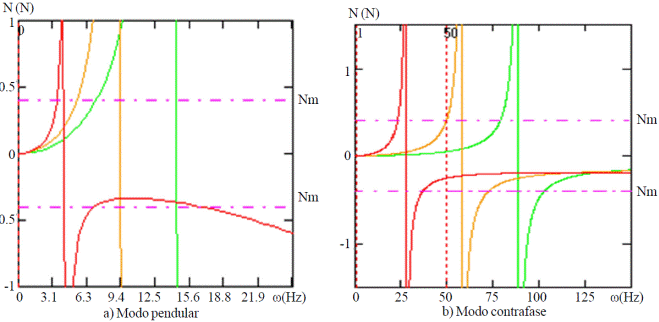
Figure 4 Frequency response of tensile strength in the abscission zone for an amplitude of the excitation of 20 mm.
In figures we can appreciate that, both in the case of the bending moment (Figure 3a) as in the case of the tensile strength (Figure 4a), to an amplitude of the excitation of 20 mm, under a pendular vibration mode where the values of internal actions required to achieve the detachment of the fruits, frequencies are narrow and close to the resonance, while under a vibration mode in antiphase (3b and 4b) these values are widely exceeded, especially in the case of bending moment, which together with the deflections which assumes the fruit-pedicel-peduncle system in the abscission zone under this mode, reaffirms the hypothesis Martinez (1977) that the bending moment that occurs in the area abscission during the vibratory movement of the fruit-stem system is the key player in the evolution of the fruit.
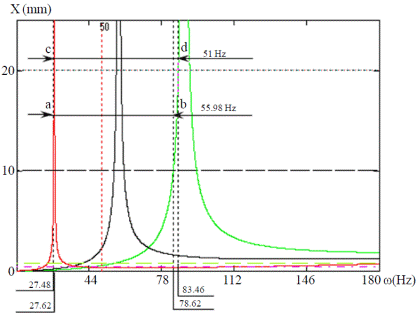
In Figure 5 the frequency response amplitude module bending moment (M) in the abscission zone 10 mm amplitude (X) excitation to handle the variety of Manila shown. It can be seen that in the case of a mode pendular vibration is sufficient amplitude of the excitation of 10 mm to achieve the release of the ripe fruit in a relatively wide frequency band 14.3 Hz around the resonance frequency of the fruits mature with physical and mechanical properties mean this without removing unripe fruits, which would divest from a frequency of 56 Hz.
This is because in that band bending moment produced by the excitement in the fruit-pedicel union, in the case of ripe fruits exceeds the value of the bending moment necessary for the release of the fruits, represented in the figure by a horizontal line discontinuous red color for mature (Mm) and green for green fruits (Mv).
Determination of rational schemes vibration
So far, both the vibration modes of the different configurations of fruits, as the response given frequency based on the model of two degrees of freedom of the fruit-pedicel-peduncle system have been obtained on the basis of average values the dimensional characteristics and physical-mechanical properties of fruits, pedicels and peduncles.
However, each of these properties has a statistical distribution, due to which, for each of the stages of fruit ripening and for each of the vibration modes, there will be a range of natural frequencies, around the frequency natural "average" which was determined based on the average values of different dimensional characteristics and physical- mechanical properties involved in the calculations. This statistical variability of the system under study is necessary to consider proposing a system of rational vibrations for selective detachment of the fruits.
The analysis was performed based on a pendulum vibration mode. In Figure 6 the frequency response module bending moment in the abscission zone of the fruit-pedicel-peduncle system in the environment of a mode pendular vibration is shown, obtained as a result of the evaluation model of two degrees of freedom with the average values of physical- mechanical system components at different stages of maturation (mature, pintones and green) properties.

Figure 6 Module frequency response in the environment of a pendulum vibration mode bending moment in the abscission zone-fruit-pedicel peduncle system in three stages of ripening mango Manila. Mean values of the physico-mechanical properties.
Figure 6 is a noticeable difference between the frequencies of "average" resonance of ripe fruits and greens is observed, being the "average" own frequency of the fruits pintones (physiological maturity) between the two, but closer to that of ripe fruits. This feature is in favor of selective harvesting, because quality standards allow harvesting the fruits pintones.
However, previously it explained that on the basis only of the frequencies of "average" resonance is not possible to establish a strategy for vibration regimes applied. Figure 7 shows that left the limit or lower resonance frequency has been determined by subtracting or increasing in σ (mean square deviation) to the mean values of the physical-mechanical ripe fruits, properties depending on whether influence the increase or decrease respectively the own frequency.
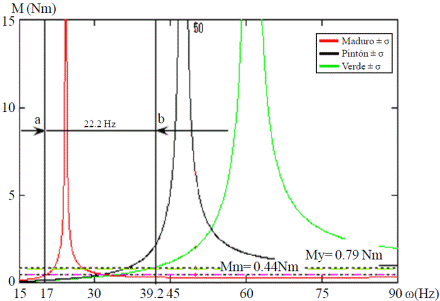
Figure 7 Module frequency responses “limits” of the bending moment in the abscission zone for an excitation amplitude of 10 mm. Oscillation mode vibration Manila handle.
In Figure 7 further show, the horizontal lines representing the required for detachment of the fruits, both mature (Mm) and green (Mv) bending moments, so that when curves frequency response bending moment each stage of maturation, are above Mm or Mv respectively straight, then have exceeded the bending moment required for the release of the fruits of that stage of maturation and therefore will be detached.
From this it can be reasoned that the intersection of the curve of frequency response bending moment in mature fruits lower resonance frequency, with the straight Mm (point a), defines a value of the frequency (17 Hz) from which ripe fruits of this variety under the excitation amplitudes of 10 mm emerge. If, starting from this value, it continues to increase the frequency of the vibrations as sweep to the frequency defined by the point b (39.2 Hz), then the ripe fruits with characteristics ranging will be understood in this band and at the same time avoid the detachment of green fruits.
The amplitude of the excitation has a marked influence on the selection of the frequency band to be applied during the selective harvesting. An increase in amplitude of the excitation results in a shift of the frequency bands. In Figure 8, it can be seen that for an amplitude of the excitation of 10 mm, the frequency sweep (defined by points a); and b) is between 27.48 to 83.46 Hz for a frequency range of 55.98 Hz. Furthermore it is seen that excessive value of the amplitude of the greatest excitement of 20 mm, can ruin the possibility of selectivity in the harvest because the frequency band is close to 51 Hz.
Conclusions
The bending for excitation amplitude of 20 mm and under a mode pendular vibration, the setting frequency (3.74 Hz) where internal actions are exceeded to achieve the release of the mature fruits is narrow and close to the resonance frequency time, confirming the hypothesis that the bending moment is the key player in the evolution of the fruit.
For a pendular mode vibration amplitude is sufficient excitation of 10 mm to achieve the release of the mature fruits in a frequency band of 14.3 Hz for the average properties physicomechanical; green fruit would divest from a frequency of 56 Hz.
When it adds or subtracts the standard deviation to the mean values of the physical-mechanical fruit, properties this influences the increase or decrease in the frequency of vibration.
The increased amplitude excitation produces a shift in the frequency bands; an excessive increase of the amplitude affects the selectivity because the frequency band narrows.
Literatura citada
Adrian, P. A and Fridley, R. B. 1965. Dynamics and design criteria of inertia type tree shakers. Transactions of the ASAE. 8(4):12-14. [ Links ]
Bobeva, M. 1972. Isledovanie otiskivaneto na malinovite plodove privibrirane. Sielskoskostopanstva Tejnika, I, Sofia. 275 p. [ Links ]
Castillo, M. A. 1995. Investigación del régimen óptimo de trabajo de los vibradores de follaje de acción vertical para el desprendimiento de naranja de Valencia en Cuba. Tesis de doctorado en Ciencia Técnicas, Universidad Agraria de la Habana, Cuba. 112 p. [ Links ]
Cooke, J. R. and Rand, R. H. 1969. Vibratory fruit harvesting: a linear theory of fruit-stem dynamic. J. Agric. Eng. 14(3):195-200. [ Links ]
Fridley, R. B. and Adrian, P. A. 1960. Some aspects of vibratory fruit harvesting. J. Agric. Eng. 41:28-31. [ Links ]
Gaskins, E. B. G. 2006. Fundamentación de los modos y los regímenes de vibración del sistema fruto-pedicelo-pedúnculo del café para la cosecha selectiva de los frutos. Tesis doctoral en Ciencia Técnicas. Universidad Agraria de la Habana, Cuba. 109 p. [ Links ]
Herrera, M. 1980. Estudio teórico de los regímenes de trabajo para el desprendimiento de guayaba por vibración. Tesis Profesional. Instituto Superior Politécnico José Antonio Echeverría, Habana, Cuba. 70 p. [ Links ]
Llanes, O. 2000. Determinación de los parámetros de diseño de vibradores inerciales de ramas para la cosecha mecanizada de cítricos. Tesis doctoral en Ciencia Técnicas. Universidad Agraria de la Habana, Cuba. 101 pp. [ Links ]
Martínez, R. A. 1977. Estudio teórico de la dinámica del sistema fruto pedúnculo. Revista Ciencias Técnicas. Serie construcción de maquinaria. Instituto Superior Politécnico José Antonio Echeverría, Habana, Cuba. Octubre. 14-16 pp. [ Links ]
Martínez, R A. 1982. Determinación de los parámetros de los órganos de trabajo para la cosecha mecanizada de naranjas por vibración. In: Proceedings of the V International Citrus Congress. Japón. 30 p. [ Links ]
Martínez, R. A.; Morales, F. J. Gómez, A. D. y Aloysius, H. N. 1989. Determinación de parámetros de un órgano de trabajo para cosecha mecanizada de café por vibración. Revista Ciencias Técnicas Agropecuarias. 2(3):27-49. [ Links ]
Rumsey, J. W. 1967. Response of citrus-stem system to fruit removing actions. MSc Tesis. University Arizona. Tucson. E. U. 85 p. [ Links ]
Varlamov, G. P. 1972. Determinación de los regímenes de trabajo de una máquina vibradora para la recogida de frutos. Trabajos del VISJOM. Moscú. 71:12-14. [ Links ]
Yung, C. and Fridley, R. B. 1975. Simulation of vibration of whole tree system using finite elements. Transaction of the ASABE. 18(3):475-481. [ Links ]
Received: March 2016; Accepted: June 2016











 texto em
texto em