Reduced design method for stabilization lagoons

Treviño Cansino, Alejandro; Cortés Martínez, Facundo; Treviño Cansino, Alejandro; Cortés Martínez, Facundo

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de ciencias agrícolas

versión impresa ISSN 2007-0934

Rev. Mex. Cienc. Agríc vol.7 no.4 Texcoco may./jun. 2016

Articles

Reduced design method for stabilization lagoons

Alejandro Treviño Cansino¹

Facundo Cortés Martínez¹^§

^¹ Facultad de Ingeniería, Ciencias y Arquitectura de la Universidad Juárez del estado de Durango. Campus Gómez Palacio, Durango. México. (atrevino@ujed.mx).

Abstract:

In Mexico stabilization lagoons represent 40% of treatment plants, most of which operate with lower or equal flow at 5 L/s. Because they are small plants, they are vulnerable to be deficient in design and operation. The article presents a reduced price for the design and review of stabilization lagoons, based in 11 equations method. The criterion considered for obtaining was expressions include variables as constant depth and evaporation also four factors were determined as a function of temperature. Reduced results are similar to the traditional method. It is recommended to continue the development of the method reduced considering the use of baffles or channels.

Keywords: reduced method; retention time; wastewater stabilization lagoons

Resumen:

En México las lagunas de estabilización representan 40% de las plantas de tratamiento, de las cuales la mayoría operan con un caudal menor o igual a 5 L/s. Debido a que son plantas pequeñas, son vulnerables a presentar deficiencias en el diseño y en la operación. El artículo presenta un método reducido para el diseño y revisión de lagunas de estabilización, con base en 11 ecuaciones. El criterio considerado para la obtención de las expresiones fue incluir las variables de profundidad y evaporación como constantes, además se determinaron 4 factores en función de la temperatura. Los resultados del método reducido son similares al tradicional. Se recomienda continuar con el desarrollo del método reducido considerando el uso de deflectores o canales.

Palabras clave: aguas residuales; lagunas de estabilización; método reducido; tiempo de retención

Introduction

Stabilization lagoons compared with other systems, wastewater treatment, they are a viable option when it has the availability of land, are efficient in removing organic matter also called biochemical oxygen demand (BOD), phosphorus, nitrogen and fecal coliforms. The latter are transmitters of diseases such as infectious hepatitis, cholera, typhoid and other important (^{Heredia, 1985}; ^{CNA and IMTA, 2007a}). The configuration of the lagoon systems relates to the combination of different types of gaps, they can be: anaerobic, facultative and maturation or polishing. For example, you can include in the design one pond (the optional) can also be considered as two: facultative and maturation. According ^{Rolim (2000)} the most complete array is three lagoons: anaerobic, facultative and maturation. The quality of wastewater in the effluent must always comply with the maximum permissible limits indicates the NOM-001-ECOL-1996 (^{DOF, 1996}).

The design method for lagoon systems adopted for Mexico, the National Water Commission (CNA) and the Mexican Institute of Water Technology (IMTA) is extensive, as it believes 23 equations, plus the design process in the maturation pond it is iterative; i.e. it proposes a hydraulic retention time and then the concentration of fecal coliform in the effluent system is verified, until it meets the limits indicated by the regulations. Because indicated it is advisable to test the method in order to reduce the number of equations; so as to obtain similar results but with less expressions. The main disadvantage of treatment systems stabilization lagoons is the great requirement terrain (^{Wood et al., 1995}; ^{Agunwamba, 2001}; ^{Mara, 2004}; ^{Kaya el al., 2007}; ^{Naddafi et al., 2009}). According ^{Mara (2001)}; ^{Mara (2004)};^{Agunwamba et al. (2003)}; ^{Hamzeh and Ponce (2007)} temperature and solar radiation promote proper treatment of wastewater in the lagoon systems.

Authors like ^{Agunwamba (1991)}; ^{Guganesharajah (2001)}; ^{U.S.
EPA, (2002)}; ^{Lloyd et
al. (2003)} and ^{Mara
(2004)} conducted studies in lagoon systems: concluded that wastewater is purified by activity of bacteria and algae. Then ^{Peña et al. (2003)}; ^{Mara (2001)} and ^{Mara
(2004)} conducted laboratory tests: included different length-width ratios and determined that the lakes with a large wide long relationship, were more efficient at removing contaminants.

According to ^{Mangelson and Watters (1972)} and ^{Lloyd et al. (2003)} in the lagoon systems hydraulic shorts are presented; i.e. residual water stagnations, so the holding time calculated in method is not adequately performed. Later ^{Band (2007)} found that the efficiency of facultative lagoons may be affected by the thermal stratification and wind speed. According to ^{Olukanni (2011)} design methods currently applied are based on the maximum load per unit area. There is a simplified design method lagoon systems: ^{Collí et al. (1992)}. The manual cited includes, in general terms, the quality of wastewater influent, process design aspects of construction, operation and maintenance.

According to ^{Noyolas et al. (2012)}, the most widely used to treat wastewater in Mexico technology is stabilization lagoons, with 40% of the plants. Besides, most treatment facilities wastewater (60%) operate with equal flows or less than 5 L/s and are classified as small plants. This confirms ^{Oliveira and von Sperling (2011)}, which mention that the main reason why the treatment plants do not meet quality standards is the deficiency in design and in operation.

The objectives of this study were to determine a reduced traditional method for designing a lagoon system with 2 ponds (facultative and maturation). Using a mathematical analysis that involves taking as constant variables that are related to temperature, then replace the variables mentioned in the formulas of traditional design method. The contribution of this study is to provide a simple calculation tool that can be applied to wastewater treatment for small communities in a region with the same environmental characteristics. It is also an extension of the simplified design method published by ^{Collí et al. (1992)}.

The paper is organized as follows: section 1, the appropriate nomenclature and the traditional design method is described. Section 2 includes the mathematical development to determine the reduced design method for lagoon systems, a summary of formulas is included. Section 3 shows an example of application, both in the traditional design method as the method reduced. Section 4: conclusions.

The traditional method considered in the design basically removing organic matter, nitrogen and phosphorus, among other parameters, in addition to fecal coliforms and helminth eggs. The method was consulted in the text: (^{CNA and IMTA, 2007a}).

Nomenclature

C.O.= organic load; Q_i= flow in the influent of the pond (m³/day); DBO_i= concentration of biochemical oxygen demand in the influent; (mg/L); 1 000= conversion factor; λν= surface organic load (gDBO₅/m³-day); T= minimum temperature monthly average of air (°C); Li= concentration of DBO₅ in the influent of the lagoon (mg/L); Af= area of the facultative pond in (m²); Qmed= influent flow in (m³/ day); Z= depth (m); V= volume (m³); O_F= mean hydraulic retention time facultative lagoon (days); X= ratio between length and width; B_Prom= average width of the gap in (m); L_Prom= average length (m); B_Sup= top width (m); levee slope= ratio of 2: 1; L_Sup= long top of the lagoon (m); A_Sup= surface area (m²); Q_e= flow in the effluent of the pond (m³/day); e= evaporation (mm/day); d= factor dispersion dimensionless; K_b= bacterial reduction coefficient (d^-1); a= constant dimensionless; Ni = fecal coliforms in the effluent from the lagoon (NMP/100 mL). Nf/No= number of fecal coliform in the effluent (NMP/100 mL); e= 2.7182818; Ne= corrected by evaporation fecal coliforms in the influent of the lagoon (NMP/100 mL); Kf= decay constant at a temperature in either (day^-1); DBOef= concentration of DBO₅ in the effluent (mg/L); DBOe= concentration of DBO₅ in the effluent from the lagoon corrected by evaporation (mg/L); O = hydraulic retention time in maturation pond (days).

Design facultative pond (dispersed flow. Method Yanez)

a) Organic load: C.O.= Qi(DBO_i)/100 1)
b) Surface design load: λs= 250(1.085)^T-20 2)
c) Facultative lagoon area: Af= 10L_i Qmed/λs 3)
d) Volume of the lagoon: V= (Af)(Z) 4)
e) Middle hydraulic retention time: O_F= V/Q_i 5)
f) Dimensioning. Length width ratio X = 3:

BProm=AfX 6)

LProm= AfBProm 7)

g) For the width and length: B_Sup= B_Prom + (Z)(Talud) 8)
L_Sup = L_Prom + (Z)(Talud) 9)
h) Calculation of surface area: A_Sup= (B_Sup)(L_Sup) 10)
i) Expenditure in the effluent: Q_e = Q_i - 0.001A_Supe 11)
j) Removal of fecal coliforms: Considering screens with length 0.70 length of the lagoon have:

X= (LProm)(0.70)(NMampF + 1) BProm/(NMampF + 1) 12)

In the case of this study screens with long width ratio X = 3 will not be considered

d= X(-0.26118 + 0.25392(X) + 1.0136(X)2 13)

k) Coefficient of bacterial reduction:
K_b= 0.841(1.075)^T-20 14)
l) Constant "a". It is determined by the formula:

a=1+4KbOFd 15)

m) Fecal coliforms in the effluent from the facultative pond.

NfNo = 4ae(1-a)/2d(1 + a)2Ni 16)

n) Fecal coliforms corrected by evaporation:
Ne=(Nf/No)(Q_i)/Q_e 17)
o) Decay constant temperature in any day:

Kf=Kf35 (1.085)35-T 18)

p) Concentration of biochemical oxygen demand in the effluent from the lagoon

DBOef=DBOiKfOF + 1 19)

q) Removal efficiency of DBO:

%=DBOi - DBOeDBOi x 100 20)

r) DBO corrected by evaporation:
DBOe= (DBO_i)(Q_i)/Q_e 21)
Lagoon maturation (dispersed flow method)
1) Hydraulic retention time (O)
2) Volume of the lagoon
V= (Q_i)(O) 22)
3) Lagoon area

A=VZ 23)

To conclude with the design of the maturation lagoon, we continue with subparagraphs f) to p) indicated in the method of facultative pond.

Simplified method proposed for the design off a cultative lagoons

To start designing a facultative pond, calculate different previous data before results of sizing and quality requirements in the effluent water.

For example: to obtain the volume, we replace surface design load (expression 2) in the area formula (equation 3) and with this we replace the volume formula (4). Then we separate the temperature-depending data as surface design load (expression 2). The values of depth and DBO are also set.

V=QizDBOi10λs 24)

The surface charge which depends on temperature, and all data known as depth Z= 1.5 m and DBO= 220 mg/L. They are replaced by a factor Beta (β): expression 25.

β=zDBOi10λs 25)

Where Beta is a factor helps to simplify the expression as shown below:

V=βQi 26)

The expression is then obtained to calculate the average area, dividing the volume (expression 26) between the depths (Z). Then equation (27) is determined.

Apromedio=βQiz 27)

A long relationship constant width X = 3 is considered. To determine the upper width of the facultative pond expression (27) is substituted into (6) and the horizontal distance representing the slope is added.

After separating Beta (β) and the known data: X= 3 and Z= 1.5 m, we replace by a factor which is called Epsilon (ε) where the expression (28) is obtained.

ε=βzX 28)

Epsilon is a temperature dependent factor that simplifies the formula (28) and is obtained as a result the expression (29):

BSuperior=εQi+1.5*pendiente 29)

To determine the long top facultative pond, the wide long relationship X = 3 by the average width is multiplied and the horizontal distance slope adds:

LSuperior=εQi+1.5*pendiente 30)

To the effluent in the lagoon formulas (29) and (30) are replaced in formula (11) and expression (31) is obtained:

Qe=Qi1-0.005β/z-0.03εQi*pendiente-0.01125*pendiente2 31)

Factors dependent on temperature and the constant are separated and replaced by omega (ω) and equation (32) is obtained.

ω=(1-0.005 β/z) 32)

Where omega is used to simplify formula (31) then:

Qe=ωQi-0.03εQi*pendiente-0.01125*pendiente2 33)

Then the formula (26) is substituted into (5) for retention time:

O_F= V/Q _i= βQ _i/Qi

O_F= β 34)

For the number of fecal coliform in the effluent (Formula 16), we consider the following:

NfNo=4ae1-a2d1+a2Ni =4ae1-a2d1+a2Ni

Constants and factors are temperature dependent and width to length ratio like a and d as separate, then they are replaced by Fi (φ) expression (33). Where we need Fi to reduce the spread factor of the equation, and is:

φ=4ae(1-a)/2d (1+a)2 35)

Fi is substituted into the above expression and corrected by evaporation (Qi/Qe), is obtained:

NfNo=φNi QiQe 36)

The BOD₅ expression (18) is simplified by separating its factors and calculated separately, also depending on temperature. Indicated is expressed as a constant Tao (τ):

DBOe=DBOiKfO+1=1KfO+1DBOi

τ=1KfO-1 37)

Result:

DBOe=τDBOi 38)

The above expression, like that for fecal coliforms, is corrected for evaporation (multiply by: Qi/Qe). Is obtained:

DBOe=τDBOiQiQe 39)

As follows, Table 1 summarizes the equations obtained with reduced criterion for the design of the facultative pond method.

Table 1 Summary of formulas for the method reduced design for facultative lagoon.

Simplified method proposed for the design of polishing lagoons

The same procedure that was included for the facultative pond, but with some differences as depth is used: 1.5 instead of 1.0 m will be used. According to ^{Rolim (2000)} depth in facultative lagoons is 1.5 to 2.5 meters. These lagoons work based on bacteria, algae and sunlight for photosynthesis; while maturation lagoons are designed with less depth: 0.6 to 1 m, in order to allow greater income from ultraviolet rays, for removal of fecal coliforms. In sizing the maturation pond beta value (retention time) it is proposed; i.e. it is an iterative system. The process stops when it meets the pollutant concentration values indicating the regulations. For the width and length above we have:

Top width

BSuperior=εQi+pendiente 40)

Top length

LSuperior=3 εQi+pendiente 41)

Expenditure in the effluent

Qe=ωQi-0.02εQi*pendiente-0.005*pendiente2 42)

To carry out the simplified design it is necessary to calculate a table of factors β, ε, ω, φ and τ (equations 25, 28, 32, 35 and 37).

You need to design a lagoon system for treating wastewater from a rural community. Population the project horizon= 1 300. A contribution is considered of 154 L/person/day (^{CNA and IMTA, 2007a}). Therefore, the design flow is 200.2 m3/ day. The temperature of the coldest month is 11.8°C (^{CNA and IMTA, 2007b}); the number of fecal coliforms in the influent is 10 000 000 00 NMP/100ml, and DBOi = 220 mg/L (^{Metcalf and Eddy, 1991}). The maximum values of contaminants mentioned regulations are: for biochemical oxygen demand (DBO) 75 mg/L, fecal coliforms 1,000 NMP/100 mL.

Results and discussion

Table 2 shows the results observed using the traditional method: the biochemical oxygen demand (DBO) and fecal coliforms in the effluent from the maturation pond. These values were consistent with stated in the regulations (^{DOF, 1996}).

Table 2 Results of the lagoon system design: facultative and maturation with the traditional method.

Figure 1 shows the measures of stabilization lagoons system based on the results as of Table 2.

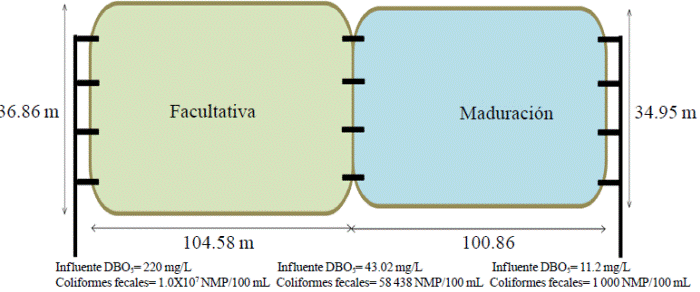
Figure 1 Dimensions of the lagoon system with the traditional method (source: contribution of the authors).

Application of simplified method of designing a facultative pond

The temperature of the coldest month is included with decimals design data: 11.8. Therefore, we proceed to calculate certain factors β, ε, ω, φ and τ. Determined in expressions (25, 28, 32, 35 and 37). Table 3 shows the factors as calculated.

Table 3 Factors calculated depending on the temperature facultative lagoon.

β	ε	ω	φ	τ
25.769013	2.39299965	0.91410329	0.00528124	0.17670417

Then applying the simplified 8 equations for the design of a facultative pond indicated in Table 1 method, we obtain:

V= (25.769013)(200.2)= 5 158.96 m³

B_Superior= (2.39299965) 200.2 + 1.5(2) = 36.86 m

L_Superior= 3(2.39299965) 200.2 + 1.5(2) = 104.58 m

A_Superficial= (36.86)(104.58) = 3,854.82 m²

Qe= (0.91410329)(200.2) - 0.03(2.39299965) 200.2 (2) - 0.01125(2)² = 180.93 m³/day

O_F = 25.769013 days

Nf/No=(0.00528124)(10,000,000) 200.2180.93 = 58,438 NMP/100 mL

DBOe= (0.17670417)(220) 200.2180.93 = 43 mg/L

As already indicated to the maturation pond retention time is proposed and factors are calculated. Table 4 shows calculated values.

Table 4 Factors calculated depending on the temperature for maturation lagoon.

Days of retention	ε	ω	φ	τ
18.01	2.45008308	0.90995639	0.01544468	0.23495835

The input data for the design of the maturation pond are: fecal coliform corrected by evaporation in the effluent from the facultative pond. 58.438 NMP/100 mL, DBO also in the effluent 43 mg/L, and. expenditure corrected by evaporation: 180.93 m³/day. With the above data and factors calculated in Table 4 apply to new account the equations shown in Table 1. As already indicated, the upper width (B_Superior), the upper length (L_Superior) and expenditure on the effluent are modified due to the depth.

V= (18.01)(180.93)= 3,258.49 m³

B_Superior=(2.45008308)(180.93 + 1.0(2)=34.95m

L_Superior= 3(2.45008308)180.93 + 1.0(2)= 100.86 m

A_Superficial= (34.95)(100.86)= 3,526 m2

Qe= (0.90995639)(180.93) - 0.02(2.45008308)180.93(2) - 0.005(2)² = 163.30 m³/day

Nf/No=( 0.01544468)(58,438)180.93163.30 = 1000 NMP/100 mL

DBOe= (0.23495835)(43)180.93163.30 = 11.2 mg/L

The implementation and results of the 11 equations reduced design method is shown. As shown, there is no difference between the results of both methods. But the small design presents fewer operations to decrease significantly the number of equations: 11 replacing 23 traditional method. Expressions of reduced proposed design method are: volume, area, top width, length top, expenses in the effluent corrected by evaporation, the hydraulic retention time, number of fecal coliform corrected by evaporation; and the biochemical oxygen demand in the effluent from both gaps.

The number of equations published in the manual ^{Collí et al. (1992)} for the design of a lagoon system; arrangement of a facultative pond plus one of maturation, is also 11. However, once the procedure has analyzed it was observed that this does not include the following: spending effluent considering evaporation, fecal coliforms and DBO also corrected by evaporation. From the above it is understood that the simplified method published by ^{Collí et al. (1992)} does not include the ratio of inclination of the slopes as well as the daily evaporation in millimeters. To determine the hydraulic retention time and prediction of organic matter using a table. The reduced design method proposed in this article, provides sufficient information for the project, in addition to the missing information in the design method published by ^{Collí et al. (1992)}. Another advantage of the proposed method is that it can determine the width and length of average and lower gaps; as it has the ratio of inclination of the levees and the depths of the lagoons.

It is important to note that the reduced method has certain limitations in its application; since the depth was considered constant at 1.5 m for the facultative pond, and one meter for maturation lagoon, plus evaporation was set to 5 mm/day. Indicated does not mean that the proposed method cannot be calculated with different depths that are recommended by the literature. The same criteria only be included in the new formula constant depth below. About influent DBO, it was set as a constant. The limit considered is the average concentration indicating literature.

Conclusions

In applying the method proposed design equations number 23, which considers the traditional design method, only 11 fell formulas. The results obtained with the design method are similar to traditional reduced.

The proposed method has some important advantages over the method published by ^{Collí et al. (1992)}: expenditure where evaporation, inclination of boards, fecal coliforms and organic matter also includes corrected by evaporation.

The analysis method proposed in this paper, was applied to the environmental conditions prevailing in the Laguna region of the state of Durango. The analysis criteria can be used in any region; but it is necessary to take into account the particular climate data. For example: temperature of the coldest month, evaporation, plus the ratio of inclination of the levees and design flow.

The proposed method is recommended to apply especially when designing with average parameters in water quality. Furthermore, this can be considered as a tool for checking the results of traditional design method. It is worth mentioning that the factors β, ε, ω, φ and τ can be pre-calculated for different temperatures to complement the small tables of factors that facilitate in calculation method. It is recommended to continue with the design method reduced lagoon systems, including baffles or channels.

Literatura citada

Agunwamba, J. C. 1991. Simplified optimal design of waste stabilization pond. Water, Air, and Soil Pollution. 59(3-4):299-309. [ Links ]

Agunwamba, J. C. 2001. Effect of tapering on the performance of waste stabilization ponds. Wat. Res. 35(5):1191-1200. [ Links ]

Agunwamba, J. C.; Ochonogar, A. and Ukpong, E. C. 2003. Experimental and principal component analysis of waste stabilization ponds. J. Appl. Sci. Eng. Technol. 3(1):25-30. [ Links ]

Banda, C. G. 2007. Computational fluid dynamics modeling of baffled waste stabilization ponds. Tesis doctoral. School of Civil Engineering, University of Leeds, UK. 1-5 pp. [ Links ]

CNA-IMTA. 2007a. Manual de diseño de agua potable, alcantarillado y saneamiento. Paquetes tecnológicos para el tratamiento de excretas y aguas residuales en comunidades rurales. CONAGUA-IMTA. Jiutepec, México. pp. 56-83. [ Links ]

CNA-IMTA. 2007b. Manual de diseño de agua potable, alcantarillado y saneamiento. Manual de diseño de lagunas de estabilización. CONAGUA-IMTA. Jiutepec, México. 234 p. [ Links ]

Collí, M. J.; Rico, M. M.; Rivas, H. A.; Escalante, E. V. E. y Luyendijk, R. 1992. Manual simplificado para el diseño, operación y evaluación de lagunas de estabilización de aguas residuales. CONAGUA-IMTA. Jiutepec, México. 36 p. [ Links ]

DOF. 1996. NOM-001-ECOL-1996. Que establece los límites máximos permisibles de contaminantes en las descargas de aguas residuales a los sistemas en aguas y bienes nacionales. SEMARNAT- Secretaría de Gobernación. D. F., México. 29 p. [ Links ]

EPA. 2002. Onsite wastewater treatment systems manual. Environmental protection agency. Office of Research and Development. EUA. 369 p. [ Links ]

Guganesharajah, R. K. 2001. Numerical aspects of computational hydraulic and water quality models for rivers, estuaries, reservoirs and aquifers with particular reference to waste stabilization ponds. Tesis doctoral. University of Surrey, UK. pp. 90-120 [ Links ]

Hamzeh, R. and Ponce, V. M. 2007. Design and Performance of Waste Stabilization Ponds. http://www.ponce.sdsu.edu. [ Links ]

Heredia, D. M. D. 1985. Tecnología moderna para el tratamiento de aguas residuales. Ingeniería Hidráulica en México. 1(1):13-20. [ Links ]

Kaya, D., Dilek, F. B. and Gokcay, C. F 2007. Reuse of lagoon effluents in agriculture by post- treatment in a step feed dual treatment process. Desalination. 215(1):29-36. [ Links ]

Lloyd, B. J.; Vorkas, C. A. and Guganesharajah, R. K. 2003. Reducing hydraulic shortcircuiting in maturation ponds to maximize pathogen removal using channels and wind breaks. Water Sci. Technol. 48(2):153-162. [ Links ]

Mangelson, K. and Watters, G. 1972. Treatment efficiency of waste stabilization ponds. J. Sanitary Eng. Division. 98(2):407-425. [ Links ]

Mara, D. D. 2001. Appropriate wastewater collection, treatment and reuse in developing countries. Proceedings of the Institutions of Civil Engineers, London. pp. 299-303. [ Links ]

Mara, D. D. 2004. Domestic wastewater treatment in developing countries. Earthscan Publications. London, England. 310 p. [ Links ]

Metcalf and Eddy (1991). Wastewater Engineering. Treatment, Disposal, Reuse., USA: Ed. McGraw-Hill. pp.124-128. [ Links ]

Naddafi, K.; Hassanvand, A. S.; Dehghanifard, E.; Faezi-Razi, D.; Mostofi, S.; Kasaee, N.; Nabizadeh, R. and Heidari, M. 2009. Performance evaluation of wastewater stabilization ponds in Arak-Iran, Iran. J. Environ. Health. Sci. Eng. 6(1):41-46. [ Links ]

Oliveira, S. C. and Von Sperling, M. 2011. Performance evaluation of different wastewater treatment technologies operating in a developing country. J. Water, San. Hygiene Development. 1(1):37-56. [ Links ]

Olukanni, D. O. 2011. Hydraulic modeling and optimization of waste stabilization ponds design for developing nations. Tesis doctoral. Covenant University, Ota, Ogun State, Nigeria. 357 p. [ Links ]

Peña, M. R., Mara, D. D. and Pignet, J. M. 2003. Improvement of mixing pattern in pilot scale anaerobic ponds treatment domestic sewage. Wat. Sci. Tech. 48(2):235-242. [ Links ]

Noyola, A.; Padilla-Rivera, A.; Morgan-Sagastume, J. M.; Güereca, L. P. and Hernández-Padilla, F. 2012. Typology of municipal wastewater treatment technologies in Latin America. Clean- Soil, Air, Water. 40(9):926-932. [ Links ]

Rolim, M. S. 2000. Sistemas de lagunas de estabilización. Como utilizar aguas residuales tratadas en sistemas de regadío. McGraw-Hill. Colombia. pp. 199-323. [ Links ]

Wood, M.; Greenfield, P. F.; Howes, T.; Johns, M. R. and Keller, J. 1995. Computational fluid dynamic modelling of waste stabilization ponds. Water Sci. Technol. 31(12):111-118. [ Links ]

Received: January 2016; Accepted: April 2016

Este es un artículo publicado en acceso abierto bajo una licencia Creative Commons