Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias agrícolas
versión impresa ISSN 2007-0934
Rev. Mex. Cienc. Agríc vol.2 no.3 Texcoco may./jun. 2011
Artículos
Habilidad de estimación de los métodos de evapotranspiración para una zona semiárida del centro de México*
Suitability of evapotranspiration estimation methods for semiarid central Mexico
Rebeca Vásquez-Méndez1§, Eusebio Jr. Ventura-Ramos1 y Jorge A. Acosta-Gallegos2
1 Posgrado en Ingeniería de Recursos Hídricos y Ambiental. Universidad Autónoma de Querétaro. Cerro de las Campanas, Querétaro, México. C. P. 76010. Tel. 01 442 1921200. Ext. 6023. (eventura@uaq.mx). §Autora para correspondencia: rebecavm@gmail.com.
2 Campo Experimental Bajío. INIFAP. Carretera Celaya-San Miguel de Allende, km 6.5. Colonia Roque, Celaya, Guanajuato, México. C. P. 38110. Tel. 01 46 16115323. Ext. 164. (acosta.jorge@prodigy.net.mx).
* Recibido: octubre de 2010
Aceptado: abril de 2011
Resumen
En zonas áridas y semiáridas, el proceso de evapotranspiración constituye una gran pérdida de agua hacia la atmósfera, por lo que existe una necesidad por entender y cuantificar este proceso, especialmente en los ambientes semiáridos donde los recursos hídricos son escasos. Muchos métodos para estimar la evapotranspiración están disponibles; sin embargo, su desempeño bajo un ambiente específico tiene que ser evaluado antes de realizar una selección. Se utilizó una estación metereológica para tomar datos de una zona semiárida del centro de México, con el propósito de evaluar ocho diferentes métodos a una escala de observación diaria, semanal y mensual. Los resultados estimados se compararon con datos medidos de un ET gage company, ya que este instrumento ha sido calibrado y probado de estar estrechamente asociado a los datos de evapotranspiración de referencia. El error absoluto medio, el error de la media cuadrática, la intercepción y pendiente de la regresión lineal y el coeficiente de determinación R2, fueron obtenidos para evaluar estadísticamente el desempeño de los métodos evaluados. Se encontró un bajo desempeño para todas las escalas de tiempo de los métodos Oudin, McGuinness, Jensen y Haise, y Romanenko, con altos valores de error absoluto medio y error de la media cuadrática. Parámetros de valores bajos de intercepción, pendiente y R2; fueron obtenidos también para estos métodos, haciéndolos impropios y por lo tanto no recomendables para el área de estudio. Por otra parte, los métodos Penman-Monteith y Penman, mostraron el mejor desempeño a diferentes escalas de tiempo. Resultados similares se han encontrado por otros autores, apoyando el método de referencia de Penman-Monteith. Se obtuvo una ecuación de regresión múltiple para predecir la evapotranspiración de referencia derivada de las variables climáticas, con valores de R2= 0.8, 0.82 y 0.91 para escalas diarias, semanales y mensuales, respectivamente, indicando la posibilidad de usar modelos de regresión para condiciones semiáridas.
Palabras clave: variables meteorológicas, evapotranspiración, ambiente semiárido.
Abstract
In arid and semiarid areas, the evapotranspiration process constitutes a major loss of water to the atmosphere, prompting the need for a better understanding and quantification of this phenomenon, especially in semiarid environments where water resources are scarce. There are many available methods to estimate evapotranspiration; however, their performance in specific environments must be evaluated before making a selection. A weather station was used to collect data from a semiarid zone of Central Mexico with the purpose to evaluate eight different methods for daily, weekly and monthly periods of observation. The estimated results were compared with measured data from an ET gage company, as this device has been calibrated and proven to be closely associated to reference evapotranspiration data. The mean absolute error, root mean squared error, regression line intercept and slope, as well as determination coefficient R2, were obtained to statistically evaluate the performance of evaluated methods. A poor performance for all time scales was found for the Oudin, McGuinness, Jensen and Haise, and Romanenko methods, with high values of mean absolute error and root mean squared error. Low values of the intercept, slope and R2 parameters were also obtained for such methods, making them not suitable and consequently not suited for the study area. On the other hand, the Penman-Monteith and Penman methods, showed the best performance in different time scales. Similar results have been fund by other authors, supporting Penman-Monteith as a method of reference. A multiple regression equation to predict reference from climatic variables was also obtained with R2= 0.8, 0.82 and 0.91 for daily, weekly and monthly scales, respectively, indicating the possibility of using regression models for semiarid conditions.
Key words: climatic variables, evapotranspiration, semiarid environment.
INTRODUCCIÓN
La evapotranspiración (ET) constituye una de las principales pérdidas de agua en regiones semiáridas, de tal manera que su evaluación o predicción es crucial para el análisis de los balances hídricos en terrenos agrícolas y con vegetación natural (Domingo et al., 1999). Dado que la disponibilidad de los recursos hídricos para la agricultura se vuelve cada vez más limitante, debido al crecimiento de la población, la competencia por parte de otros usos de agua, la ocurrencia de sequía y degradación de la calidad del agua, la importancia de la evapotranspiración como un componente mayor del uso de agua en la agricultura es cada vez más significativa (García et al., 2004). La cuantificación de la evapotranspiración es importante para el desarrollo de estrategias efectivas para la conservación del suelo y agua (Aydin, 2008).
Los modelos de predicción pueden ser usados para estimar las pérdidas de agua para diferentes ambientes y clima, pero su desempeño, tanto espacial y temporalmente, tiene que ser evaluado antes de que se usen en condiciones específicas. Aunque varios métodos han sido propuestos para estimar ET, no hay un consenso universal sobre la adecuabilidad de alguna ecuación específica para un clima dado, y normalmente requieren de calibraciones locales rigurosas (DehghaniSanij et al., 2004; Ahmadi y Foodlandmand, 2008).
El modelo de Penman-Monteith es probablemente el método más ampliamente aceptado para la estimación mensual de la evapotranspiración de referencia (ET0). Aunque este método es apropiado para diferentes climas; el cálculo de ET0 requiere de varios datos de entrada, tales como valores mínimos y máximos de temperatura, humedad relativa, horas de insolación, velocidad del viento, y radiación solar (Allen et al., 2006; Ahmadi y Foodlandmand, 2008).
La radiación solar es importante y ha sido considerado como uno de los principales parámetros de entrada en muchos estudios de simulación (Bandyopadhyay et al., 2008). Varios investigadores han caracterizado los sitios de estudio con el propósito de predecir ET usando diferentes modelos de ET (Oudin et al., 2005; Douglas et al., 2009). Una muestra de 308 cuencas localizados en Australia, Francia y los Estados Unidos fue utilizada para el estudio de Oudin et al. (2005) con el propósito de optimizar un método para la evapotranspiración potencial (ETP) en un modelo lluvia-escurrimiento.
La selección del método para áreas semiáridas no es tarea sencilla; en tales regiones, la precipitación presenta típicamente una gran variabilidad espacial y temporal, y la cuantificación de la ET es difícil y constituye una fuente significativa de incertidumbre en el balance regional hídrico (Contreras et al., 2008). El componente de evapotranspiración ha sido probablemente el componente más difícil de cuantificar y medir experimentalmente (Cui y Zornberg, 2008). Uno de los métodos utilizados más simples es de Thornthwaite, el cual requiere sólo de datos de temperatura. Sin embargo, se ha encontrado que este método subestima la ET en zonas áridas y la sobreestima en climas húmedos ecuatoriales (Ahmad y Foodladmand, 2008). Además, el método necesita la calibración del factor k para diferentes climas (Al-Ghobari, 2000).
El método de Priestley-Taylor usa el coeficiente α, el cual necesita ser calibrado para diferentes áreas y variables climáticas (Lhomme, 1997). Las redes neuronales artificiales (RNA) usadas en el norte de Irán, consideran variables como la temperatura mínima y máxima, así como la radiación extraterrestre (Rahimikhoob, 2009). En general, la cuantificación de la ET ha sido conducida típicamente usando aproximaciones de balance de energía o métodos indirectos de balance hídrico. En el semiárido central mexicano, las mediciones de ET son muy limitadas o no están disponibles.
Por lo tanto, es necesaria una evaluación de modelos selectos aplicables en zonas semiáridas, así como su desempeño para diferentes intervalos de tiempo. El objetivo de este estudio fue evaluar diferentes métodos para estimar la evapotranspiración de referencia (ET0) y comparar los resultados con la evapotranspiración medida con un atmómetro (ET gage, model E), para diferentes escalas de tiempo en un ambiente semiárido. En adición, se realizó un análisis de regresión entre los datos observados de ET y variables climáticas relacionadas.
MATERIALES Y MÉTODOS
Área de estudio
El área de estudio se localiza en Cadereyta de Montes, en el estado de Querétaro, en un ambiente semiárido típico del Centro de México (clima BS, en la clasificación de Köppen), localizado en las coordenadas 99° 46' 46'' longitud oeste y 20° 43' 49'' latitud norte a 2 069 msnm. La vegetación predominante en la región son el bosque tropical caducifolio y nopaleras. La temperatura y precipitación media anual son 17 °C y 480 mm respectivamente, tal como lo reporta INEGI (1996).
Toma de datos
La evapotranspiración se midió con un atmómetro (ET gage, Modelo E), instalado a una altura de 1.2 m. Los atmómetros han sido usados exitosamente en la estimación de la evapotranspiración bajo diferentes ambientes (Shanon, 1968; Broner y Law, 1991; ErvinyKoski, 1997; Gavilan y Castillo-Llanque, 2009). Los periodos de monitoreo incluyeron de mayo a noviembre de 2006 y de mayo a octubre de 2008, en concordancia con la estación de lluvias y como consecuencia con mayor dinámica de la humedad del suelo. Los datos de temperatura del aire, humedad relativa, presión barométrica, velocidad de viento y radiación solar, fueron obtenidos usando una estación meteorológica con datalogger (CR1000, Campbell Scientific Co.), localizada en el sitio de estudio.
La evapotranspiración del ET gage y todos los datos climáticos fueron registrados automáticamente cada 20 min. Ocho modelos de evapotranspiración potencial fueron usados para estimar ET y fueron comparados con los valores observados. Las ecuaciones generales para los métodos seleccionados se observan en la Cuadro 1.
Descripción de los métodos
El método de Penman (1948) fue desarrollado con una base aerodinámica, en la cual se considera que la evaporación se debe al transporte turbulento de vapor por un proceso de difusión tipo Eddy y una base de energía, de tal manera que la evaporación es uno de los mecanismos de degradación de la radiación incidente. Fue originalmente probado en América y Europa, pero usado posteriormente en el resto del mundo. Los datos de entrada son: horas de insolación, temperatura, humedad relativa y velocidad del viento.
Jensen y Haise (1963) desarrollaron un método para su uso en campos irrigados de zonas áridas y semiáridas del oeste de los Estados Unidos, cuyo desempeño fue adecuado en la región húmeda del este central. Expresaron los componentes verticales individuales en una ecuación de balance de energía para una zona con vegetación de cultivos. Así mismo, introdujeron el componente ET/Rs, que representa los efectos combinados de reflectancia. La ecuación combina un enfoque de balance de energía con coeficientes determinados empíricamente. El método es ampliamente usado por su simplicidad. Este método usa como variables de entrada la radicación y la temperatura media.
McGuinness y Bordne (1972) compararon varios métodos para estimar la ETP a partir de curvas "estándar" obtenidas de lisímetros, como una forma de seleccionar los métodos más apropiados de estimación para áreas húmedas (Parmele y McGuinness, 1974). El método usa temperatura y radiación extraterrestre.
Hargreaves y Samani (1982) observaron que los parámetros más importantes en la estimación de ET son la temperatura y radiación solar. Su método utiliza la temperatura y latitud en una ecuación simple para su determinación. Su desempeño fue evaluado en una escala semanal y mensual, para diferentes latitudes.
Wright (1982) propuso el método de Kimberly-Penman, el cual es un enfoque modificado del método de Penman, que incluye el efecto del viento y depende del movimiento diario de éste, considerando factores empíricos relacionados con la aerodinámica de la superficie de la vegetación (α), la naturaleza general de la localidad y la velocidad del viento en 24 horas a una altura z. El método fue utilizado en un ambiente árido con estimaciones diarias.
El método de Penman-Monteith (Allen et al., 1998) también se basa en el método de Penman (1948). El modelo usa el balance y flujo de energía, y considera la ecuación de referencia a nivel mundial. Este método utiliza un gran número de variables. La información de entrada es la radiación neta, la velocidad del viento, temperatura, presión de saturación de vapor y presión real del vapor.
Oudin et al. (2005) propuso un método con el objetivo de desarrollar una ecuación simple dentro de un modelo lluvia-escurrimiento. Los autores encontraron que los modelos de McGuinness y Bordne, Jensen y Haise eran más relevantes para la modelación lluvia-escurrimiento que los modelos tipo Penman. El método fue evaluado en varias localidades utilizando parámetros mensuales.
Estimación del error
Los valores de ET estimados con los modelos, fueron comparados con los valores observados utilizando estadísticos estándar y análisis de regresión. El error medio absoluto (EMA) y la raíz del error de la media cuadrática (REMC), fueron calculados con:
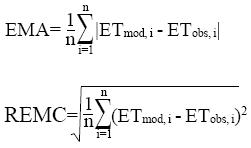
Donde: ETmod, i y ETobs, i= valores del modelo y datos observados respectivamente, para cada día i, y n es el número total de días (semana o mes). EMA y REMC, están en unidades de mm día-1, son indicadores agregados del desempeño del modelo, mientras que los estadísticos de regresión (pendiente, intercepto, R2) son indicadores de predicción de los modelos de la ET en una escala de tiempo (Douglas et al., 2009; Gavilán y Castillo-Llanque, 2009).
RESULTADOS Y DISCUSIÓN
Información climática
Para los dos años de evaluación, la información climática registrada tuvo el siguiente comportamiento: 2006 fue un año húmedo por arriba de la normal, con una precipitación total de 774 mm, mientras que 2008 fue un año normal con 504 mm. La temperatura del aire varió de 5 a 26°C y de 4 a 22°C para el 2006 y el 2008 respectivamente, con una media de 15 °C en ambos años. La humedad relativa varió de 17 a 86% en 2006 y de 35 a 87% en 2008. Por otro lado, la radiación neta medida para 2006 varió de 0.12 a 16.14 MJ m-2 día-1, mientras que el rango correspondiente para 2008 fue de 0.89 a 18.8 MJ m-2 día-1. Las horas de insolación variaron de 3 a 12 h día-1 para ambos años. Estas condiciones climáticas son comparables con las condiciones existentes en otras regiones semiáridas del mundo con latitudes similares (Al-Ghobari, 2000; Bayala et al., 2008).
En general, los valores de evapotranspiración medidos con el atmómetro variaron de 1 a 8.5 mm día-1, con un promedio de 3.5 mm día-1 durante el periodo de monitoreo en ambos años. Estos valores caen dentro del rango reportado para ambientes áridos y semiáridos con clima moderado (2-4 mm) y clima cálido (4-8 mm) por Allen et al. (1998) y Rahimikhoob (2009). La evapotranspiración acumulada fue de 525 y 413 mm, en 2006 y 2008 respectivamente para el periodo correspondiente.
Desempeño de los modelos
El error medio absoluto y la raíz del error de la media cuadrática a nivel diario, semanal y mensual, para cada modelo se pueden observar en la Cuadro 2. Para el análisis, los métodos evaluados fueron agrupados en tres categorías con base en los valores de EMA y REMC: i) menor de 1 mm día-1; ii) entre 1-2 mm día-1; y iii) más de 2 mm día-1.
A escala diaria (n= 272) el modelo de Penman, con un valor de EMA de 0.98, fue el único incluido en el grupo de menos de 1 mm día-1, con el mejor desempeño a este nivel dentro de los métodos evaluados. El segundo grupo estuvo conformado por los modelos de Penman-Monteith, Oudin, Hargreaves y Samani, y McGuinness y Bordne con valores de EMA de 1.09, 1.1, 1.2 y 1.6 mm día-1 respectivamente. Estos modelos se desempeñaron relativamente bien; sin embargo, su aplicación debe considerar otros elementos de análisis. El grupo con valores de EMA mayores de 2 mm día-1 lo conformaron los modelos Kimberly-Penman, Jensen & Haise y Romanenko con valores de EMA de 2.17, 2.66 y 2.66 mm día-1 respectivamente. El desempeño de los últimos modelos no se considera satisfactorio para una estimación a nivel diario en las condiciones de estudio.
A escala semanal (n= 47) los valores de EMA se redujeron en alrededor de un 14.5% (±1.4) para los grupos de menos de 1 y de entre 1-2 mm día-1. En consecuencia, los valores de EMA para los métodos de Penman, Oudin y Penman-Monteith fueron 0.84, 0.92 y 0.93 mm día-1 respectivamente. Así, estos métodos pueden ser recomendados para regiones semiáridas similares en base a los valores del EMA. Los valores de EMA correspondientes para los métodos Hargreaves y Samani, McGuinness y Bordne fueron 1.05 y 1.36 mm día-1 respectivamente. No se observó una reducción significativa en los valores de EMA a nivel semanal para el grupo de más de 2 mm día-1, que no implicó una mejora en su desempeño a este intervalo; su uso bajo estas condiciones debe hacerse con precaución.
A escala mensual (n= 12) los valores de EMA se redujeron alrededor de 27% (±3.1) en comparación con los datos diarios para los grupos de menos de 1 y de entre 1-2 mm día-1. Los modelos Penman, Oudin, Penman-Monteith, Hargreaves y Samani presentaron valores de EMA de 0.71, 0.76, 0.78 y 0.91 mm día-1 respectivamente, mientras que los valores de EMA para el modelo McGuinness y Bordne fueron de 1.22 mm día-1. De forma similar a la escala semanal, no se observó una reducción significativa en los valores de EMA para los modelos de Kimberly-Penman, Romanenko, Jensen y Haise, los cuales presentaron valores de EMA de 2.2, 2.5 y 2.6 mm día-1 respectivamente. Los modelos de Jensen y Haise, Kimberly- Penman fueron desarrollados para condiciones semiáridas; sin embargo, su desempeño a nivel diario, semanal y mensual no fue satisfactorio.
La REMC es un indicador de la habilidad de desempeño de un modelo en un periodo de tiempo dado (Douglas et al., 2009). La REMC fue calculada a nivel diario, semanal y mensual. A nivel diario, los mejores modelos fueron Penman, Penman-Monteith, Hargreaves y Samani, Oudin, McGuinness y Bordne con valores REMC de 1.27, 1.31, 1.43, 1.44 y 1.83 mm día-1; mientras que el desempeño de los modelos Kimberly-Penman, Romanenko, y Jensen y Haise no fueron satisfactorios, presentando valores de REMC de 2.57, 2.96 y 2.97 mm día-1.
La ampliación del periodo de observación a una semana mejoró el desempeño del primer grupo, reduciendo los valores de REMC en alrededor de 14.3% (±2). Los nuevos valores de REMC para los modelos Penman, Penman-Monteith, Oudin, Hargreaves y Samani, y McGuinness y Bordne fueron de 1.08, 1.09, 1.23, 1.27 y 1.57 mm día-1 respectivamente. El desempeño de los modelos Kimberly-Penman, Jensen y Haise, y Romanenko no mejoro para el análisis semanal, obteniendo valores de 2.54, 2.76 y 2.77 mm día-1 respectivamente.
El análisis mensual mejoró aún más el desempeño de los métodos Penman, Penman-Monteith, Oudin, Hargreaves y Samani, y McGuinness y Bordne con valores de REMC de 0.89, 0.95, 0.99, 1.09 y 1.45 mm día-1 respectivamente. En general, la reducción en la magnitud de la REMC para este grupo fue de alrededor del 30% (±4.3) en comparación con los datos diarios, lo que los hace apropiados para su uso en condiciones semiáridas. Nuevamente los modelos Kimberly-Penman, Jensen y Haise, y Romanenko presentaron los más altos valores de la REMC (2.41, 2.69 y 2.7 mm día-1 respectivamente), indicando un desempeño pobre en las condiciones estudiadas.
En general, los métodos Penman y Penman-Monteith presentaron los valores más bajos de EMA y REMC. Estos métodos incluyen un número considerable de variables de entrada, lo que resulta en un mayor desempeño con respecto a los valores observados de ET. Por otro lado, los métodos de Oudin, Hargreaves y Samani, McGuinness y Bordne presentaron un desempeño similar, considerando que incluyen pocas variables, pueden ser una opción para condiciones semiáridas; sin embargo, se deben considerar otros aspectos específicos antes de tomar la decisión final sobre su aplicación. Con base a los valores de EMA y REMC, los métodos Kimberly-Penman, Jensen y Haise, Romanenko, presentaron los índices de error más grandes, a pesar de su simplicidad, están limitados dadas las condiciones del estudio.
La relación entre los valores observados y predichos de evapotranspiración a una escala diaria, semanal y mensual se muestra en la Figura 1. Basado en el análisis de regresión, idealmente se espera un intercepto cerca de cero, pendientes de línea de regresión y coeficientes de determinación cercanos a la unidad (Douglas et al., 2009). Excepto por el método de Kimberly-Penman, el cual obtuvo un valor para el intercepto de la línea de regresión de 0.54, el resto de los métodos presentó valores de 2 a 5, indicando una desviación significativa de este punto, sin diferencias significativas para el análisis diario, semanal y mensual.
Con respecto a la pendiente de las líneas de regresión, todos los valores fueron menores de 0.5 para el análisis diario de los datos. El valor de la pendiente aumentó sustancialmente para los métodos Penman-Monteith, y Jensen y Haise cuando el análisis de regresión se realizó con datos semanales y mensuales. El resto de los métodos presentaron valores menores a 0.5 lejos del valor unitario esperado. Esto indica una correspondencia pobre entre los valores observados y predichos, reflejados como una desviación de la línea 1-1.
El coeficiente de determinación para el análisis diario indicó una correlación baja entre los valores observados y predichos para todos los métodos. Los valores más grandes de R2 correspondieron a los métodos de Kimberly-Penman, Penman-Monteith y Penman con un R2= 0.61, R2= 0.65 y R2=0.67, respectivamente, mientras que para el método de Hargreaves y Samani R2 fue de 0.55, y para Oudin, McGuiness y Bordne, Jensen y Haise, y Romanenko el valor fue de R2= 0.22 para todos los casos. Irmak et al. (2005) reportaron valores bajos de R2 para Penman-Monteith en Estados Unidos, aunque Gavilán y Castillo-Llanque (2009) reportaron valores altos en Europa para los métodos Penman-Monteith, y Hargreaves y Samani.
Gavilán y Castillo-Llanque (2009) observaron que los datos de evapotranspiración en promedios semanales se ajustaron mejor entre el modelo Penman-Monteith y los valores observados con el ET gage, para ambientes semiáridos. A nivel semanal, los valores del coeficiente de determinación incrementaron 10% para los modelos Penman-Monteith y Penman, con valores de R2= 0.78 y R2=0.73, respectivamente. Por otro lado, para el método Kimberly-Penmann, el valor de R2 fue 0.61, mientras que para los métodos de Hargreaves y Samani, Oudin, McGuiness y Bordne, Jensen y Haise, y Romanenko, el incremento en los valores de R2 fueron del orden del 25%, sin que esto significara una correlación significativa entre valores observados y predichos, ya que la magnitud varió entre R2= 0.58 y R2= 0.52.
A nivel mensual, el coeficiente de determinación incrementó un 20% con respecto a los datos diarios para los métodos Penman-Monteith y Penman, con valores de R2= 0.81 y R2= 0.88, respectivamente. Por otro lado, el aumento respectivo para Hargreaves y Samani, y Kimberly-Penman fue de aproximadamente 10% con valores de R2= 0.7 y R2= 0.64, respectivamente. Aunque el valor del coeficiente de determinación aumentó en aproximadamente un 10% para los métodos Jensen y Haise, Oudin, McGuiness y Bordne, y Romanenko, con valores no significativos de R2 entre 0.5 y 0.55. Estos métodos siguen sin poder ser recomendados debido al bajo desempeño en el análisis de series de tiempo.
En general, los métodos Jensen y Haise, McGuiness y Bordne, y Oudin, mostraron valores bajos de R2 en las diferentes escalas de tiempo. Estos métodos son similares, con pequeñas diferencias en algunos factores (dependiendo de la temperatura media y la radiación extraterrestre). El método de Romanenko tampoco cambió su desempeño respecto a la escala de tiempo. El grado de asociación entre los valores observados y predichos aumentó con la escala de tiempo en los modelos, donde se incluyeron los factores Rn, es, ed, velocidad de viento y temperatura media. Así, el mayor grado de asociación se encontró para los modelos Penman y Penman-Monteith, seguidos del método Kimberly-Penman.
Los coeficientes de determinación indican el grado de asociación entre los valores observados y medidos de ET. Sin embargo, la correspondencia de valores solo puede alcanzarse si se utilizan factores de ajuste. Los factores de ajuste promedio para los métodos estudiados se presentan en la Cuadro 3. Los valores medios fueron 1.09 para Penman, 0.83 para Penman-Monteith, 2.69 para Kimberly-Penman, 0.82 para Hargreaves y Samani, 1.1 para Oudin, 0.75 para McGuiness y Bordne, 0.58 para Jensen y Haise, y 0.58 para Romanenko. El uso de estos factores proporciona más certidumbre si los modelos se usan en condiciones similares, los valores obtenidos por el modelo necesitan dividirse por su respectivo factor de ajuste para obtener un resultado calibrado.
Evapotranspiración medida y variables climáticas
El desempeño de los modelos fue adecuado y posteriormente mejorado usando el factor de calibración. Sin embargo, otra alternativa para predecir ET es por medio de análisis de regresión con datos climáticos (Allen et al., 1998). Los coeficientes de correlación de Pearson (R2) fueron 0.53, 0.58, -0.68 y 0.72, para la relación entre ET y la temperatura, velocidad del viento, humedad relativa y radiación neta, respectivamente (Cuadro 4). No se encontró una correlación significativa entre ET y la presión atmosférica. Gao et al. (2006); Khoob (2008) encontraron evidencias indicando que el proceso de evapotranspiración es altamente influenciado por la temperatura, humedad relativa, velocidad del viento, y que presentaba efectos locales y estacionales.

La significancia de las variables se vio nuevamente reflejada en el modelo resultante de la regresión lineal múltiple usando el método Stepwise en SPSS v13 (Cuadro 5). Las variables más significativas en los modelos de regresión obtenidos fueron la humedad relativa y la radiación neta, con un R2 de 0.74. El modelo puede ser mejorado al incluir variables adicionales, tal como se observa en la Tabla 5, donde la inclusión de la temperatura media y la velocidad del viento resultó en un aumento con R2= 0.8.
CONCLUSIONES
La evapotranspiración medida con un ET gage en el sitio de estudio para el periodo de mayo a noviembre del 2006 fue de 525 mm. El valor correspondiente para el periodo de mayo a octubre de 2007 fue de 413 mm. El valor mayor de ET (8.5 mm) fue registrado en mayo del 2006, mientras que el valor más bajo (1 mm) correspondió a noviembre de ambos años. Los valores diarios y mensuales de ET0 fueron similares a los reportados por otros autores para regiones semiáridas.
Los métodos Oudin, Jensen y Haise, McGuinness y Bordne, Romanenko, mostraron valores altos de REMC y EMA, y valores bajos de pendiente, intercepto y R2. El poco desempeño de estos modelos no cambió con el análisis para diferentes escalas de tiempo. En consecuencia, no se recomienda su uso para las condiciones climáticas similares a las dominantes en el sitio de estudio, a menos que se realice un análisis específico. El método Hargreaves and Samani tuvo un mejor desempeño a nivel mensual que el grupo anterior de modelos, con un R2 de 0.7 y el uso para estimaciones diarias no fue adecuado.
Los modelos tipo Penman (Penman-Monteith y Penman) mostraron el mejor desempeño para las diferentes escalas de tiempo, con valores bajos de REMC y EMA, y con valores más grandes de R2. El desempeño de este tipo de modelos mejoró a escala semanal y mensual, como lo indica el incremento en el valor de R2.
Los datos climáticos para predecir la evapotranspiración son: radiación solar, temperatura del aire, velocidad del viento y humedad relativa; las cuales predicen la evapotranspiración de referencia con valores de R2 alrededor de 0.8, 0.82 y 0.91 para estimaciones diarias, mensuales y semanales, respectivamente.
LITERATURA CITADA
Ahmadi, S. H. and Fooladmand, H. R. 2008. Spatially distributed monthly reference evapotranspiration derived from the calibration of Thornthwaite equation: a case study, South of Iran. Irrig. Sci. 26:303-312. [ Links ]
Al-Ghobari, H. M. 2000. Estimation of reference evapotranspiration for southern region of Saudi Arabia. Irrig. Ssci. 19:81-86. [ Links ]
Allen, R. G.; Pereira, L. S.; Raes, D. and Smith, M. 1998. Crop evapotranspiration: guidelines for computing crop requirements. FAO Irrigation and Drainage Paper No. 56. Rome, Italy. [ Links ]
Aydin, M. 2008. A model for evaporation and drainage investigations at ground of ordinary rainfed-areas. Ecol. Modell. 217:148-156. [ Links ]
Bandyopadhyay, A.; Bhadra, A.; Raghuwanshi, N. S. and Singh, R. 2008. Estimation of monthly solar radiation from measured air temperature extremes. Agric. For. Meteorol. 148:1707-1718. [ Links ]
Bayala, J.; Heng, L. K.; Van Noordwijk, M. and Ouedraogo, S. J. 2008. Hydraulic redistribution study in two native tree species of agroforestry parklands of West African dry savanna. Acta Oecologica. 34:370-378. [ Links ]
Broner, I.; and Law, R. A. P. 1991. Evaluation of a modifed atmometer for estimating reference ET. Irrig. Sci. 12:21-26. [ Links ]
Contreras, S.; Boer, M. M.; Alcalá, F. J.; Domingo, F.; García, M.; Pulido-Bosch, A. and Puigdefábregas, J. 2008. An ecohydrological modelling approach for assessing long-term recharge rates in semiarid karstic landscapes. J. Hydrol. 351:47-57. [ Links ]
Cui, Y. J. and Zornberg, J. G. 2008. Water balance and evapotranspiration monitoring in geotechnical and geoenvironmental engineering. Geotech. Geol. Eng. 26:783-798. [ Links ]
DehghaniSanij, H.; Yamamoto, T. and Rasiah, V., 2004. Assessment of evapotrasnpiration estimation models for use in semiarid environments. Agric. Water Manage. 64(2):91-106. [ Links ]
Domingo, F.; Villagarcía, L.; Brenner, A. J. and Puidefábregas, J. 1999, Evapotranspiration model for semi-arid shrub-lands tested against data from SE Spain. Agric. For. Meteorol. 95:67-84. [ Links ]
Douglas, E. M.; Jacobs, J. M.; Sumner, D. M. and Ray, R. L. 2009. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 373:366-376. [ Links ]
Ervin, E. H., and Koski, A. J. 1997. A comparison of modified atmometer estimates of turfgrass evapotranspiration with Kimberly-penman alfalfa reference evapotranspiration. Int. Turfgrass Soc. Res. J. 8:663-670. [ Links ]
Gao, G.; Chen, D.; Ren, G.; Chen, Y. and Liao, Y. 2006. Spatial and temporal variations and controlling factors of potential evapotranspiration in China: 1956-2000. J. Geogr. Sci. 16(1):3-12. [ Links ]
García, M.; Raes, D.; Allen, R. and Herbas, C. 2004. Dynamics of reference evapotranspiration in the Bolivian highlands (Altiplano). Agric. For. Meteorol. 125:67-82. [ Links ]
Gavilán, P. and Castillo-Llanque, F. 2009. Estimating reference evapotranspiration with atmometers in a semiarid environment. Agric. Water Manage. 96:465-472. [ Links ]
Hargreaves, G. H. and Samani, Z. A. 1982. Estimating potential evapotranspiration. Technical note. J. Irrig. Drain. Eng. 108(3):225-230. [ Links ]
Instituto Nacional de Estadística, Geografía e Informática (INEGI), 1996. Cuaderno Estadístico Municipal. Cadereyta de Montes, Estado de Querétaro. H. Ayuntamiento Constitucional de Cadereyta de Montes. [ Links ]
Jensen, M. E. and Haise, H. R. 1963. Estimating evapotranspiration from solar radiation. J. Irrig. Drain. Div. ASCE 89(LR4). Proceedings of the America Society of Civil Engineers.15-41 pp. [ Links ]
Khoob, A. R. 2008. Artificial neural network estimation of reference evapotranspiration from pan evaporation in a semiarid environment. Irrig. Sci. 27:35-39. [ Links ]
Lhomme, J. P. 1997. A theoretical basis for the Priestley-Taylor coefficient. Boundary-Layer Meteorol. 82:179-191. [ Links ]
McGuinness, J. L. and Bordne, E. F. 1972. A comparison of lysimeter-derived potential evapotranspiration with computed values. TB1452. U. S. Department of Agricultural. Technical Bulletin. Num. 1452. 71 pp. [ Links ]
Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F. and Loumagne, C. 2005. Which potential evapotranspiration input for a lumped rainfall-runoff model?. Part 2-Towards a simple and efficient potential evapotranspiration model for rainfall-runoff modeling. J. Hydrol. 303:290-306. [ Links ]
Parmele, L. H. and McGuinness, J. L. 1974. Comparison of measured and estimated daily potential evapotranspiration in a humid region. J. Hydrol. 22:239-251. [ Links ]
Penman, H. L. 1948. Natural evaporation from open water, bare soil and grass. Proceedings of the Royal Society of London. 193:120-145. [ Links ]
Rahimikhoob, A. 2009. Estimation of evapotranspiration based on only air temperature data using artificial neural networks for a subtropical climate in Iran. Theor. Appl. Clim. 101:83-97. [ Links ]
Romanenko, V. A. 1961. Computation of the autumn soil moisture using a universal relationship for a large area, Proc. Ukrainian Hydrometeorological Research Institute. Kiev. No. 3. [ Links ]
Shannon, J. W. 1968. Use of atmometers in estimating evapotranspiration. J. Irrig. Drain. Div. Am. Soc. Civ. Eng. 94:309-320. [ Links ]
Wright, J. L. 1982. New evapotranspiration crop coefficients. J. Irrig. Drain. Eng. 108:57-74. [ Links ]














