Introduction
In industry and services, supply systems have a high degree of complexity, owing to the existence of the multiple relations that each element has with others within the same system. In consequence, it is often observed that work should be done with a network of stations/plants, warehouses/suppliers, containers/distribution centers and customers. Throughout such a network not only materials but also information circulates (Bhaskar and Lallement, 2010).
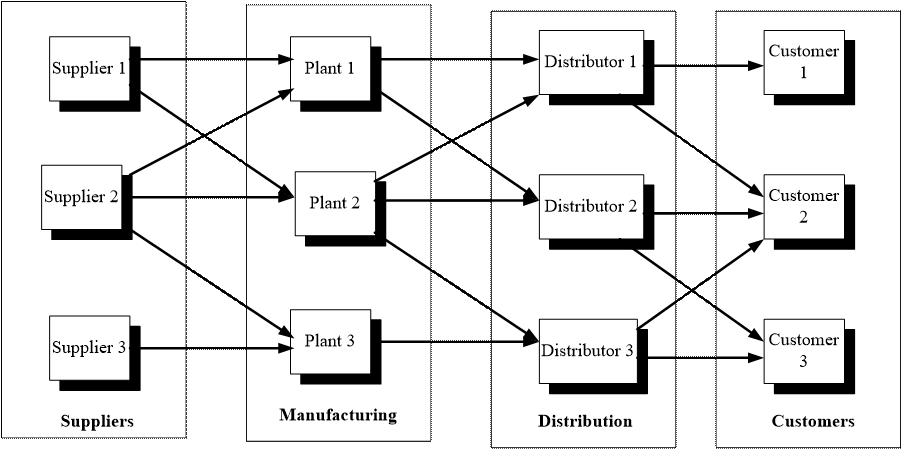
Some examples of the decisions that the administrators of these systems have to take are: how much product should be manufactured or how much should be sent from each workplace to the following link in the chain, with the total cost of dispatch being the common performance measurement (Figure 1). Consider also a cross-docking system where goods and materials are transferred without actually entering the warehouse or being put away into storage (Kulwiec, 2004); a manager must determine the service time or the number of servers that reduces the residence time within the facilities, in other words the cycle time in the system.
Optimal network design plays an important role in the supply chain operation, as good logistic distribution network can save transportation costs as well as improve service levels (Marmolejo, Rodríguez, Cruz-Mejía & Saucedo, 2016). The minimum cost network flow model is a useful tool for analyzing these types of systems.
It is worth mentioning that the nodes in a network, such as the one mentioned above are usually stations that provide a service, in other words, we are talking about queuing networks. Analytical queuing models are used for determining properties such as work in progress, time in the system (cycle time), congestion of the system, measuring the quality of the service as well as quantifying the operating cost of said systems.
Networks may be open (the customers can enter and leave through any station on the network) or closed (the customer circulates around the network). Queuing network models are employed to represent not only production or manufacturing lines or, but also service and supply chain systems (Bolch, Greiner, de Meer and Trivedi, 2006).
Problem
The minimum cost network flow model only takes the transport costs into account; however every node on the network is often a station that provides a service (a factory, a warehouse). This operation generates a service cost (the products have to be manufactured) and a cost for the time taken to be served (the orders follow a service discipline and a queue is formed). In this context, managers and practitioners also need information about cycle time, work-in-process as well as the availability of resources at plants and warehouses. For a given topology of plants, warehouses and demand centers, it is evident that the solution obtained by a minimum cost flow model will change if each node is considered as a queueing system but, how much is the difference?; how sensitive is the solution if practitioners include transportation cost, waiting cost and service cost; what a practitioner and a manager can expect if they wish to measure supply chain performance as queueing networks.
Background
Most papers on queuing networks focus on the determination of the properties of the networks and use both analytical means and simulation. These models can be used for finding properties, control, planning and optimization, which is the case with this paper.
In the paper of Pourbabai, Blanc and van der Duyn Schouten (1996) a modified version is presented of the minimum cost flow model together with the respective version of the maximum network flow problem with stations where queues form. Their paper proposes the probability of meeting service levels as a constraint.
Kerbache and MacGregor Smith (2000) propose a mathematical programming model that determines the optimum path that maximizes the throughput, the properties are calculated by applying the Generalized Expansion Method. Given that this is a mixed integer nonlinear model, an algorithm is developed to find good solutions, Yenisey (2006) applies concepts from Pourbabai et al (1996) to construct a mathematical programming model for MRP systems.
MacGregor Smith (2011) considers M/G/c, M/G/c/c systems and proposes a procedure for finding the optimum flow paths in a queuing network: In this case, the objective function is the system’s throughput and is applied to the modeling of passenger flow in underground transport systems.
Morabito, de Souza and Vázquez (2014) propose an analytical method for the shortest path problem in G/G/c queuing networks as well as the application of equations to improve the accuracy of the calculations of the system’s properties, while, when applicable, the objective function also maximizes the throughput of the system. van Woensel T., Cruz F.R.B. (2014) extended the model to G/G/c/K networks to determine the shortest route in systems with multiple servers.
Some examples of applied cases we can mention are Bhaskar and Lallement’s paper (2010) for the analysis of the supply chain of an Indian textile company, Srivathsan and Kamath (2012); they propose a model for the analysis of supply chains, but raise the idea of using the model to plan and find the optimum values of decision variables. He and Hu (2014) propose a model for decision-making in disaster prevention systems for the Shanghai area, while Beard and Chamberlain (2013) employ the principles proposed in Pourbabai. et al (1996) for the analysis of the flow of information in computer network systems.
Other analytical techniques for the modelling of supply chains are Petri Nets, Series parallel graphs, Markov chains and system dynamics (Srinivasa &Viswanadham, 2001).
This paper’s contributions are:
This paper is a variant on the proposal of Pourbabai, et al (1996), but in this case the queuing and node operating costs are included in the objective function.
It differs from Morabito, Souza and Vázquez’s paper (2014) in that different versions of the cost model are employed and assessed; the analysis is, for the moment, confined to the fact that the service time and demand follow an exponential distribution.
We apply the decomposition principle to obtain the performance measures. MacGregor Smith (2011), Morabito, et al. (2014), or van Woensel T., Cruz F.R.B. (2014) use General Expansion Method.
We are contributing with an approach for the process of modeling and analysis of a supply chain as a network of queues.
We obtain an optimal solution and calculate the work in process and cycle time of proeuction orders.
Numerical examples are solved and the results are compared with those obtained from a conventional minimum cost flow model. Simulation is used to validate analytical results of cycle time and work-in-process.
This paper is of interest to administrators and/or people in charge of supply chains, purchasing schedulers or production schedulers and is useful for decision-making in the medium or long time. With this model we get information about the cycle time, the work in process and the congestion at each station as well as the quantity of a product that must be sent to each customer in the network, minimizing the total operating cost of the system, this approach takes ino account the uncertainty of demand and service time of plants and distributors.
The minimum cost network flow problem
Consider a directed network that consists of a finite set of nodes N and a set of directed arcs A that join pairs of N nodes. Arc (i, j) is said to be incident to nodes i and j and is directed from node i to node j. Every node i is assigned a number f i that represents the available supply of an article (f > 0) or the demand for some article (f < 0). Nodes with supply are known as source nodes and the demand nodes are known as destination nodes. If f i = 0 then it is a transfer node, given that there is no supply or demand at said node.
Each arc is associated with a value x
ij
that is the flow of material from node i to node j and a constant c
ij
that is the cost of circulating through said arc. We shall that the total supply and the total demand are equal, in other words
Minimize:
Subject to:
The constraints (2) are called network flow conservation equations. In conservation equations, the term
The equations require the net flow that leaves node i to be equal to f i . Finally, it must be pointed out that there can be flow capacity through the arcs.
The minimum cost flow model can be used to represent a logistics network where people and/or materials move through various points, the movement of locomotives, communications systems, oil pipelines, tanker schedules, etc (Bazaraa, Jarvis and Sherali, 1974, Wagner, 1975).
The minimum cost network flow problem can be posed as a linear programming problem and the simplex method can be applied to find the optimum solution for a particular instance.
One of the assumptions in the aforementioned flow model is that no operation is done in the nodes and that the material flows without undergoing any kind of delay. However the people in charge of the administration and planning of the operations must take into account the time customers and materials spend in a queue at the station while waiting for the corresponding service; the time required to process a product, order or job; and the cost of the service, while they must also determine and analyze the system’s properties such as the amount of work in process (WIP) and the cycle time in the system (from the time when the order is received until it is delivered to the end customer).
The aforementioned properties are performance measurements for queuing networks. A summary of the method for calculating said properties is given below.
Queuing networks
A queuing network is one where there are at least two stations connected to each other (Figure 2). Each node on the network represents a resource (for example a station or a factory). In this paper we use the following premises:
Properties of queuing networks
Assume a network of n stations, the transit of the customers from one station to another is defined by the transit matrix P where each element p ij is the probability that the customer goes from station i to station j. P is a square matrix. Assume that, through node i, γ 0i customers per unit of time can enter the network from the exterior. Therefore the total flow to any node i on the network satisfies the following expression (Buzacott and Shanthikumar, 1993, Curry and Feldman, 2011, Bolch et al, 2006):
Expressing this result in a matrix form:
Where γ and λ are the flow column vectors from the exterior to each node and the entry flow to the node, respectively and P T is the transpose of the probability matrix. The system can be solved to obtain the entry flows to each station λ:
Where I is the identity matrix. As can be observed, given γ and P, the equation calculates the entry flows to each station on the network.
Quadratic coefficients of the entry flows
After the Equation (4), the entry flow to each station is made up by two elements: the entry from outside to the system through node i and the flow from any station within the network.
Assume that the external flow to a node j has a coefficient of variation that is denoted as
If the station has s servers, and each customer requires
Once again this approximation can be expressed in matrix form and is solved as a system of linear equations, whose solution shall be:
Where each element of the matrix Q is calculated as follows:
And each element of the vector β is obtained with:
Once the flows and their respective coefficient of variation have been obtained, the next step will consist of assessing the properties of each one of the network’s station applying the decomposition principle. The expressions for the cycle time of station i and variability of departure from station i are:
A summary of the procedure is given in Figure 3 (Buzacott and Shanthikumar, 1993, Curry and Feldman, 2011).
Cost function in a queuing network
The operating cost of a queuing network is expressed by the following equation:
Conventionally, only the service cost and queuing cost are included in the operating cost (OC) in a queuing network. Likewise, only the network flow cost is included in a minimum cost flow problem.
Equation (13) includes the three terms: the cost arising from the operation of the servers (
As can be appreciated, flow x ij between pairs of nodes is calculated using (4). Assuming that the external flows only appear at the supply nodes, then the term γ 0i is zero, and the flow for any node other than the supply nodes is:
Optimization model
Assume that we have a network with a set of nodes
The material receives a transformation at each node that, on average, requires
There is no external flow to the demand nodes. Moreover, reflows are only considered for representing reprocesses, whereas exits from the system through any node other than the demand nodes are not considered.
The flow between the network’s stations can be represented as a probability matrix P.
There is a service cost, Service Cost i , for serving or producing a product unit, and there is also a cost per unit of work in process, Work in process Cost i . Finally there is also a cost for transiting from one station to another c ij . The proposed optimization model is as follows:
Minimize:
Subject to:
The quantity of material that should circulate between pairs of nodes or stations should be determined in such a way as to minimize the value of operation cost (16). It is worth mentioning that in the model, the decision variable is the probability or fraction
The flow is constrained to the entry - throughput balance at each node (17) being satisfied, as well as to the flow in the system being such that the congestion or used capacity at each station ρ (used capacity or congestion) are fulfilled or, if not, to ρ < 1 for all the stations (18).
Likewise, the way in which the flow is directed through the network is constrained to the range given in (19). In the model, the constraint (20) ensures that the material does not leave the network through any node that is not a demand node. In any event this constraint can be modified if necessary. The flows are calculated using (21).
The problem of routing customers, packets and other entity flows in finite queueing networks is an integer nonlinear programming. Our model is a variant of the Optimal Routing Problem in queueing networks which is known to be NP-hard (MacGregor Smith and Daskalaki, 1988, Kerbache and MacGregor Smith, 2000). The proposed model can incorporate constraints for the work in process or the cycle time. It is also feasible that the service time of one or more stations and the number of servers are also decision variables.
It is worth mentioning that, like any model, it is necessary to be careful to take the necessary factors into account and thus avoid situations such as getting a very complex model that does not have a feasible solution.
This model can be applied to the analysis and solution of problems involved with the planning of supply chain operations, using a networks approach and properties, such as the cycle time, work in process, the load at the stations or production or processing centers.
Implementation on a spreadsheet
It was necessary, for the study, to construct a spreadsheet template using the steps of the aforementioned Figure 3.
The template automatically calculates the total entry flows of each node using the Equations (4), (5), (6); the flows through each arc with their respective cost; the costs of the stations; cycle time and amount variability of departures of each station; as well as the total operating cost of the system using the equations (7), (8), (9), (10), (11), (12).
Work in process of each station is obtained with Little’s Law:
The template allows us to model systems that have up to 10 stations with a network arrangement or else with a pure series arrangement. Further details will be encountered in Appendix 1.
Numerical examples
A numerical analysis was carried out of several cases with a proposed minimum cost flow model, estimating properties (Work in process and cycle time), while the results were validated using simulation.
All cases were built taking into account that the maximum number of stages that are considered in mathematical models of supply chains are four (Olhager, Pashaei and Sternberg, 2015). Case A is a conventional minimum cost flow model without operation at the nodes. In series B, the minimum cost flow model with operation at the nodes was studied with and without costs (Table 1).
Table 1 Cases studied
| Case | Operation at the nodes | Cost flow | Cost of service and queuing | Decision variable |
|---|---|---|---|---|
| A | No | Yes | No | Flow at each arc x ij |
| B1 | Yes | Yes | No | Fraction p ij that is sent from node i to node j. The flow is calculated using (13). |
| B2 | Yes | Yes | No | Fraction p ij that is sent from node i to node j and service time at each node. The flow is calculated using (13). |
| B3 | Yes | Yes | Yes | Fraction p ij that is sent from node i to node j. The flow is calculated using (13). |
| B4 | Yes | Yes | Yes | Fraction p ij that is sent from node i to node j and service time at each node. The flow is calculated using (13). |
In case B1, decision variables are the probabilities p ij of the customer going from node i to node j. In case B2, the decision variables are p ij as well as the service time at each station or node. In case B3, which is the model with service cost and queuing cost, the decision variable is the fraction p ij that travels between pairs of nodes.
Finally, in model B4, the decision variables are the fraction p ij that travels between pairs of nodes and the service time at each station or node.
To validate each analytical result from series B (flows, WIP and cycle time), we used a simulation model that was constructed in the Arena simulation software. Five independent replications were done. The run length was chosen to obtain a 95% confidence interval of WIP and cycle time. The details of the model and the data for the repeated samples are given in Table 2. An example is given of the model in Figure 4 as an illustration.
Table 2 Characteristics of the simulation model
| Simulation time (95% confidence) | 5000 days |
| Replications | 5 per series B case |
| Calculated properties | Work in process and cycle time |
| Probability function for service time | Exponential |
| Probability function for demand | Exponential |
Series A
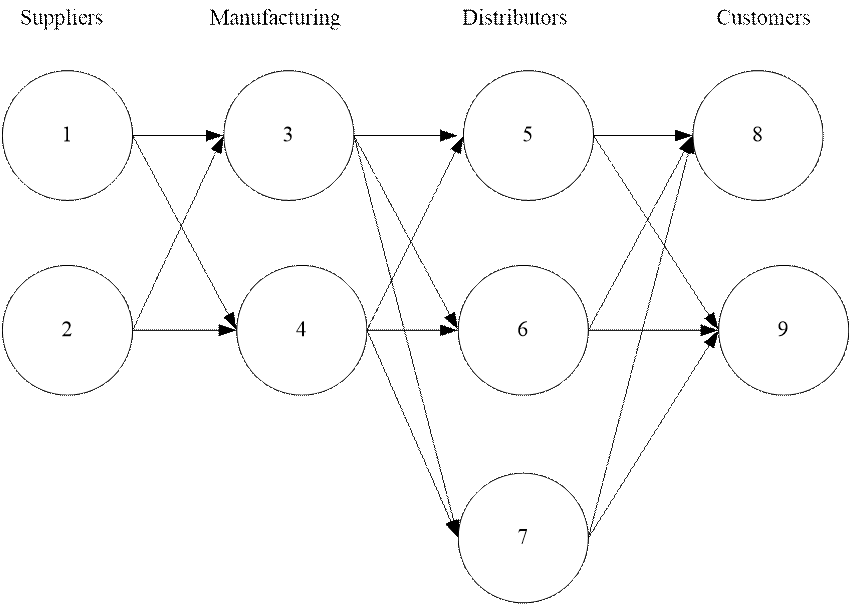
Consider a system such as that of Figure 5. Nodes 1 and 2 are the sources of the supply, nodes 3 and 4 are manufacturing nodes, 5, 6 and 7 are transfer nodes and nodes 8 and 9 are the demand nodes.
The costs per unit transported between pairs of nodes are given in Table 3. The demand at nodes 8 and 9 is 30 units, while the supply available at nodes 1 and 2 is 30 units.
Table 3 Origin - destination costs
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | $ 25.0 | $50.0 | |||||||
| 2 | $33.0 | $29.0 | |||||||
| 3 | $22.0 | $17.0 | $21.0 | ||||||
| 4 | $20.0 | $20.0 | $19.0 | ||||||
| 5 | $20.0 | $12.0 | |||||||
| 6 | $14.0 | $13.0 | |||||||
| 7 | $12.0 | $11.0 |
On solving the minimum cost flow model, using Solver and the data, we get the solution given in Figure 6: 30 units should be sent from node 1 to node 3, and 30 units from node 2 to node 4. 30 units shall be sent from node 3 to node 5, 30 units shall be sent from node 4 to node 7.
Finally node 5 shall send 30 units to demand node 9 and node 7 shall supply 30 units to demand node 8 (Table 4). The operating cost is $3570.
Series B. Minimum cost flow model with operation at the nodes
The analysis of the system is presented below, incorporating the data about the operation at each node, as well as the constraints on flow and use of the capacity.
Case B1
Consider the above minimum cost flow problem, taking into account that the nodes are stations where the customers receive a service, the data corresponding to the service time at each station are given in Table 5.
Table 5 Service time and standard deviation of the service time at each node
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| T S | 0.01 | 0.028 | 0.027 | 0.03 | 0.06 | 0.03 | 0.03 |
| σ Ts | 0.01 | 0.028 | 0.027 | 0.03 | 0.06 | 0.03 | 0.03 |
We will assume, in this case, that the service times are exponentially distributed, there are only transport costs between stations and that there is only one server at each node.
The decision variable is fraction p ij which must be sent from station i to station j, this value is used to calculate amount of the flow of material between each station (Table 6).
Table 6 Constraints of case B1
| 0.25≤p i ≤0.90,i=1,2,3,4,5,6,7 | Used capacity constraint |
| 0.25≤p 13 ≤1,0.25≤p 14 ≤1 | Constraints for the proportion that has to move through arc ij |
| 0.25≤p 23 ≤1,0.25≤p 24 ≤1 | |
| 0.25≤p 35 ≤1,0.25≤p 36 ≤1,0.25≤p 37 ≤1 | |
| 0.25≤p 45 ≤1,0.25≤p 46 ≤1,0.25≤p 47 ≤1 | |
| 0.25≤p 58 ≤1,0.25≤p 59 ≤1 | |
| 0.25≤p 68 ≤1,0.25≤p 69 ≤1 | |
| 0.25≤p 78 ≤1,0.25≤p 79 ≤1 | |
| -(λ 5 p 58 +p 6 λ 68 +λ 7 p 78 )=-30 | Node 8 demand constraint. Node 9 demand constraint |
| -(λ 5 p 59 +p 6 λ 69 +λ 7 p 79 )=-30 | |
| λ 1 p 13 + λ 1 p 14 =30 | Constraint for supply nodes 1 and 2. Node 3 flow constraint. Node 4 flow constraint. |
| λ 2 p 23 + λ 2 p 24 =30 | |
| λ 3 p 35 + λ 3 p 36 + λ 3 p 37 -( λ1p 13 + λ 2 p 23 )=0 | |
| λ 4 p 45 + λ 4 p 46 + λ 4 p 47 -( λ 1 p 14 + λ 2 p 24 )=0 |
The constraints for the value of p ij are given in Table 6. For this example in particular, the used capacity is constrained to the (25% - 90%) range.
In this case we assume that the total demand of nodes 8 and 9 is shared out equally between nodes 1 and 2 (this could be the result of a decision taken beforehand by the person in charge in accordance with some prior criterion) in consequence, the entry flow to said stations is 30 each. The same Table 6 shows the flow constraints for the supply nodes 1 and 2, as well as the demand nodes 8 and 9. Of transfer nodes 3 - 7, only the equations corresponding to nodes 3 and 4 are shown.
The flows between stations were obtained by running the Solver complement and are given in Table 7.
Table 7 Flow per arc
| Arc | 1 - 3 | 1- 4 | 2- 3 | 2 - 4 | 3- 5 | 3 - 6 | 3 - 7 | 4 - 5 |
|---|---|---|---|---|---|---|---|---|
| Fraction | 0.750 | 0.250 | 0.25 | 0.75 | 0.25 | 0.50 | 0.25 | 0.25 |
| Flow | 22.500 | 7.500 | 7.50 | 22.50 | 7.5 | 15 | 7.50 | 7.50 |
| Arc | 4 - 6 | 4 - 7 | 5 - 8 | 5 - 9 | 6 - 8 | 6 - 9 | 7 - 8 | 7 - 9 |
| Fraction | 0.25 | 0.50 | 0.250 | 0.750 | 0.41 | 0.59 | 0.75 | 0.25 |
| Flow | 7.50 | 15 | 3.75 | 11.25 | 9.37 | 13.13 | 16.88 | 5.63 |
| Operating cost | $3,776.25 | |||||||
The first significant point is the fact that the flow between stations is not an integer value, unlike a conventional minimum cost flow model. In the new solution, unlike Case A, the flow is distributed throughout the network (Figure 7).
The flow between stations requires the sending of material from station 1 to 4 and from station 2 to 3. The same happens with the flow from 3 to 5, 3 to 6, 3 to 7, 4 to 6, 4 to 7, 5 to 8, 6 to 8 and 7 to 9.
The operating cost obtained, being $3,776.25, is higher, which represents a difference of $206.25 or 2.8% in respect of case A. It is worth mentioning that this is normal as, owing to the conditions imposed on each node and the flow between stations, arcs were employed that had not been considered, thus raising said cost.
Additional information is obtained with model B1 for the administrators and decision-makers: We observe, for example, that station 1 is only used at 30% of its used capacity ( or congestion); stations 2 and 3 are used at 84 and 81% of their capacity, respectively; while stations 6 and 7 are used at 67.5% of their capacity (Table 8).
Table 8 Properties in each node: analytical vs simulation
| Sta. | Capacity (%) | Cycle time (days) | Work in process (units) | Capacity (%) | Cycle time (days) | Work in process (units) |
|---|---|---|---|---|---|---|
| Analytical | Simulated | |||||
| 1 | 30.0% | 0.014 | 0.429 | 30.79% | 0.014 | 0.4375 |
| 2 | 84.0% | 0.175 | 5.250 | 86.18% | 0.239 | 7.34 |
| 3 | 81.0% | 0.142 | 4.263 | 81.32% | 0.143 | 4.33 |
| 4 | 90.0% | 0.300 | 9.000 | 90.81% | 0.277 | 8.44 |
| 5 | 90.0% | 0.600 | 9.000 | 90.15% | 0.539 | 8.33 |
| 6 | 67.5% | 0.092 | 2.077 | 66.70% | 0.091 | 2.055 |
| 7 | 67.5% | 0.092 | 2.077 | 65.89% | 0.085 | 1.935 |
| Property | Analytical | Simulated | Difference | |||
| Work in process | 32.10 | 32.91 | 2.46% | |||
| Total Cycle time | 0.535 | 0.5428 | 1.4% | |||
One relevant factor is the identification of the bottleneck. One accepted definition establishes that the bottleneck is the station where the most work in process is to be observed (Lawrence and Buss, 1995). In this example, stations 4 and 5 can both be considered to set the limits for the production capacity, as they are used at 90% of their capacity.
The cycle time for the process is the total time that elapses from the moment when the production order is received until it arrives at its destination with the customer: In the example, the total cycle time is 0.535 days and if we assume a basis of 1 month= 30 days, then the cycle time will be 16.05 days.
The amount of work (customers or production orders queuing in front of the station waiting for service) in the overall process is 32.096.
As regards the properties obtained by simulation, the work in process obtained by the analytical method differs by -2.46% in respect of results of the simulation, while the cycle time differs by-1.43%.
Case B2
The flows and cost that were found by analytical methods are given in Table 9.In this case we observe that on being compared with case B1, the solution obtained presents several changes in both the flows and the properties of the system.
Table 9 Flow at each node
| Arc | 1 - 3 | 1- 4 | 2- 3 | 2 - 4 | 3- 5 | 3 - 6 | 3 - 7 | 4 - 5 |
|---|---|---|---|---|---|---|---|---|
| Fraction | 0.750 | 0.250 | 0 | 1 | 0.25 | 0.50 | 0.25 | 0.25 |
| Flow | 22.500 | 7.500 | 0 | 30 | 5.63 | 11.25 | 5.63 | 9.38 |
| Arc | 4 - 6 | 4 - 7 | 5 - 8 | 5 - 9 | 6 - 8 | 6 - 9 | 7 - 8 | 7 - 9 |
| Fraction | 0.25 | 0.50 | 0.250 | 0.750 | 0.386 | 0.617 | 0.75 | 0.25 |
| Flow | 9.38 | 18.75 | 3.75 | 11.25 | 7.97 | 12.66 | 18.28 | 6.09 |
| Operating cost | $3744.78 | |||||||
In the flows we observe, for example, that the arc 2 - 3 is not used. The total operating cost, which in this case is only the flow between pairs of nodes, is less in respect of case B1, presenting a reduction in cost of 0.84%.
As regards the performance measurements, case B2 presents a bottleneck at stations 4 and 5, where both are employed at 90% of their capacity, also there is a drop in the work in process and time cycle (Table 10).
Table 10 Optimum service time and properties at each node: analytical vs simulation
| Sta. | Optimum service time (days) | Capacity (%) | Cycle time (days) | Work in process (units) | Capacity (%) | Cycle time (days) | Work in process (units) |
|---|---|---|---|---|---|---|---|
| Analytical | Simulated | ||||||
| 1 | 0.01 | 30.00% | 0.014 | 0.429 | 29.90% | 0.014 | 0.423 |
| 2 | 0.028 | 84.00% | 0.175 | 5.25 | 83.80% | 0.186 | 5.571 |
| 3 | 0.027 | 60.80% | 0.069 | 1.548 | 59.80% | 0.068 | 1.507 |
| 4 | 0.024 | 90.00% | 0.24 | 9 | 90% | 0.244 | 9.200 |
| 5 | 0.06 | 90.00% | 0.6 | 9 | 91% | 0.648 | 9.750 |
| 6 | 0.03 | 61.90% | 0.079 | 1.623 | 61.20% | 0.080 | 1.651 |
| 7 | 0.03 | 73.10% | 0.112 | 2.721 | 73.28% | 0.113 | 2.773 |
| Property | Analytical | Simulated | Difference | ||||
| Work in process | 29.57 | 30.88 | 4.24% | ||||
| Total cycle time | 0.493 | 0.5152 | 4.30% | ||||
A saving of 5.7% is obtained in the cycle time and there is a reduction of 5.67% in the work in process with respect to case B1.The analytical results for the work in process and the cycle time differ by -4.24% and -4.30%, respectively.
Cases A, B1 and B2 are comparable with each other. Figure 8 shows the comparison in cost of case A with cases B1 and B2. The cost of model B2 gives a better solution than case B1, which means it is worth considering the service time as a variable in order to improve the performance of the system.
As we have already mentioned, case A gives a lower cost, however this does not imply that it is a better solution, on the contrary, this is because additional elements are being incorporated into the model, to with: constraint on the flow, constraints on each node; all the above results in the feasible region shrinking.
Case B3
This model incorporates the service costs and queuing cost at each station. The values, which are given in Table 11, are arbitrary as the only criterion for assigning them was for the queuing cost to be more expensive than the service cost. The rest of the model does not have any alterations. The comparisons shall only be made with model B4, which is described further on.
Table 11 Service cost data and queuing cost
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Service Cost | $5 | $3 | $16 | $10 | $4.50 | $8 | $8 |
| Queueing cost | $6.50 | $15 | $17 | $15 | $12 | $13 | $11 |
With the flows given in Table 12, the properties of the system are shown below: used capacity, cycle time and work in process (Table 13).
Table 12 Flow through each arc
| Arc | 1 - 3 | 1- 4 | 2- 3 | 2 - 4 | 3- 5 | 3 - 6 | 3 - 7 | 4 - 5 |
|---|---|---|---|---|---|---|---|---|
| Fraction | 0.750 | 0.250 | 0.292 | 0.708 | 0.25 | 0.5 | 0.25 | 0.25 |
| Flow | 22.500 | 7.500 | 8.765 | 21.235 | 7.82 | 15.64 | 7.82 | 7.18 |
| Arc | 4 - 6 | 4 - 7 | 5 - 8 | 5 - 9 | 6 - 8 | 6 - 9 | 7 - 8 | 7 - 9 |
| Fraction | 0.250 | 0.50 | 0.250 | 0.750 | 0.421 | 0.578 | 0.75 | 0.25 |
| Flow | 7.184 | 14.36 | 3.75 | 11.25 | 9.62 | 13.21 | 16.63 | 5.54 |
Table 13 Properties in each node: analytical vs simulation
| Sta. | Capacity (%) | Cycle Time (days) | Work in process (units) | Capacity (%) | CycleTime (days) | Work in process (units) |
|---|---|---|---|---|---|---|
| Analytical | Simulated | |||||
| 1 | 30.0% | 0.014 | 0.429 | 29.43 | 0.014 | 0.417 |
| 2 | 84.0% | 0.175 | 5.250 | 84.52 | 0.187 | 5.63 |
| 3 | 84.5% | 0.174 | 5.434 | 82.97 | 0.154 | 4.75 |
| 4 | 86.2% | 0.217 | 6.225 | 85.64 | 0.208 | 5.98 |
| 5 | 90.0% | 0.600 | 9.000 | 89.14 | 0.528 | 7.92 |
| 6 | 68.5% | 0.095 | 2.171 | 67.32 | 0.091 | 2.04 |
| 7 | 66.5% | 0.090 | 1.989 | 67.32 | 0.088 | 1.95 |
| Property | Analytical | Simulated | Difference | |||
| Work in process | 30.496 | 28.712 | 6.21% | |||
| Total cycle time | 0.508 | 0.48201 | 5.3% | |||
The first significant fact are the overall results obtained for cycle time and work in process, which are lower than those for case B1. The work in process obtained of 30.496 units is 1.60 units fewer, which represents a 5 % reduction. In the case of the cycle time, the result is 0.508 days and represents a difference of 0.027 units; once again if we assume that 1 month =30 days, then the new cycle time is 15.248 days and represents a 5% improvement in respect of case B1.
Here it is worth mentioning that a desirable goal for any administrator is to shorten the customer's queuing time and decrease the inventory in process. In both cases the customer would perceive an improvement in the service they receive: less of a wait to receive their product or else less of a wait to be served.
We can also see that there is only one bottleneck in this example and this is at station 5, which is at 90% of its capacity, having on average 9 units in a queue, which is followed, in terms of holdups, by stations 2, 3 and 4.
The analytical results for the work in process now show a difference of 6.21% and in the case of the cycle time, of 5.3% in respect of the results obtained by simulation.
As for the costs, having analyzed Table 14 in detail, we observe that station 3 represents 26.7% of the total costs and what stands out is that this has the highest service cost, in other words, service is expensive at this station. Furthermore, when we look at the queuing cost column, we can see that station 5 has the highest congestion cost, therefore, from a monetary perspective, queuing at this station is the most expensive.
Table 14 Analysis of cost per station
| Station | Service cost | WIP cost | $ Total / station | % |
|---|---|---|---|---|
| 1 | $500.00 | $2.79 | $502.79 | 19.6% |
| 2 | $107.14 | $78.75 | $185.89 | 7.2% |
| 3 | $592.59 | $92.37 | $684.97 | 26.7% |
| 4 | $333.33 | $93.37 | $426.71 | 16.6% |
| 5 | $75.00 | $108.00 | $183.00 | 7.1% |
| 6 | $266.67 | $28.22 | $294.88 | 11.5% |
| 7 | $266.67 | $21.87 | $288.54 | 11.2% |
Table 15 shows the costs of transport, the operating cost of the stations and the total cost of the system. In this example in particular, the cost of the transport represents approximately 60% of the total cost.
Table 15 Overall costs
| Operating cost of the stations | $2566.78 | 40.44% |
| Transport cost | $3,781.69 | 59.56% |
| Total operating cost | $6,348.47 |
Conventionally in a queuing network, an administrator focuses their attention on the bottleneck, however and as we can see in the results described above, there are other considerations that should not be ruled out.
In a situation like the one in the example being analyzed, the decision-maker has several possible directions where they could propose improvements: they can take individual (service, congestion) costs into account; consider the overall cost; focus on suggesting improvements either to temper the effect of the production bottleneck or for the cost of transport which, in this case, represents 60% of the system’s total operating cost.
Case B4
In this variant we must now determine the service times for stations that minimize the cost of flow in the network and take the values p ij between pairs of nodes as fixed, so there is no change in the flows. The values are taken from the model B3 solution and Table 16 shows the flows that are obtained by analytical methods.
Table 16 Flow through each arc
| Arc | 1 - 3 | 1- 4 | 2- 3 | 2 - 4 | 3- 5 | 3 - 6 | 3 - 7 | 4 - 5 |
|---|---|---|---|---|---|---|---|---|
| Fraction | 0.750 | 0.250 | 0 | 1 | 0.25 | 0.5 | 0.25 | 0.5 |
| Flow | 22.500 | 7.500 | 0 | 30 | 5.63 | 11.25 | 5.63 | 18.75 |
| Arc | 4 - 6 | 4 - 7 | 5 - 8 | 5 - 9 | 6 - 8 | 6 - 9 | 7 - 8 | 7 - 9 |
| Fraction | 0.250 | 0.25 | 0.250 | 0.750 | 0.613 | 0.387 | 0.75 | 0.25 |
| Flow | 9.38 | 9.38 | 6.09 | 18.28 | 12.66 | 7.97 | 11.25 | 3.75 |
The second column in Table 17 shows the optimum service time. Looking at the results of case B4 we can see that the solution tends to balance the used capacity of each station: stations 2, 5, 6 and 7, at least, show very little difference between each other.
Table 17 Optimum service time and properties at each node: analytical vs simulation
| Sta. | Optimum service time (days) | Capacity (%) | Cycle time (days) | Work in process (units) | Capacity (%) | Cycle time (days) | Work in process (units) |
|---|---|---|---|---|---|---|---|
| Analytical | Simulated | ||||||
| 1 | 0.028 | 82.77% | 0.160 | 4.804 | 82.22% | 0.147 | 4.437 |
| 2 | 0.024 | 71.01% | 0.082 | 2.449 | 70.74% | 0.086 | 2.555 |
| 3 | 0.037 | 82.15% | 0.205 | 4.601 | 81.97% | 0.182 | 4.045 |
| 4 | 0.022 | 83.33% | 0.133 | 5.000 | 83.42% | 0.135 | 5.051 |
| 5 | 0.031 | 75.14% | 0.124 | 3.023 | 74.07% | 0.118 | 2.847 |
| 6 | 0.038 | 78.08% | 0.173 | 3.562 | 79.23% | 0.185 | 3.892 |
| 7 | 0.051 | 76.76% | 0.220 | 3.303 | 76.85% | 0.230 | 3.460 |
| Property | Analytical | Simulated | Difference | ||||
| Work in process | 26.74 | 26.38 | 1.36% | ||||
| Total cycle time | 0.445 | 0.439 | 1.36% | ||||
In this case the bottleneck is to be found at station 4 where the used capacity is 83.33%, followed by stations 1 and 3.
Station 3 contributes with 31.9% of the total costs of the system, followed by station 4 (Table 18).
Table 18 Analysis of cost per station
| Sta. | service-cost | Queuing cost | $ Total / station | % |
|---|---|---|---|---|
| 1 | $ 181.23 | $ 31.22 | $ 212.45 | 9.9% |
| 2 | $ 126.74 | $ 36.74 | $ 163.48 | 7.6% |
| 3 | $ 592.76 | $ 92.20 | $ 684.96 | 31.9% |
| 4 | $ 352.84 | $ 65.62 | $ 418.47 | 19.5% |
| 5 | $ 95.96 | $ 28.46 | $ 124.42 | 5.8% |
| 6 | $ 231.28 | $ 48.71 | $ 279.99 | 13.0% |
| 7 | $ 221.62 | $ 44.18 | $ 265.80 | 12.4% |
It is worth pointing out that both the transport cost and the operating cost of the stations are slightly lower than the ones obtained in case B4 (Table 19).
Table 19 Overall costs
| Operating cost of the stations: | $2,049.94 | 36.24% |
| Transport cost | $3,779.53 | 63.76% |
| Total operating cost | $ 5,829.47 |
Cases B3 and B4 are compared in Figure 9. We can again see that it is a good idea to treat the service time as a variable, as this makes it possible to get a better solution: The savings in costs we obtain through finding the optimum service time and the optimum flow between stations is 6.58%, while the time cycle decreases by 10.83%. The comparison of B3 and B4 with cases A, B1 and B2 is not considered valid because said models represent other systems as they do not include either service costs or queuing costs.
Conclusions
The incorporation of new elements into a known model enriches the information that can be extracted on obtaining its solution.
In the case of the networks flow, the conventional minimum cost flow model can be expanded by assuming that each node is a station that provides a service j has a mean of Ts. In this case the addition of elements from the queuing networks makes it possible to obtain additional information about how the resources are being employed as well as, for example, getting metrics such as the time cycle and quantity of work in process. Equations of queeing systems take into account the stochastic component of a supply chain.
In this paper we tested a model for a single product and a single server, and can be applied to the analysis of a supply chain, however it can be broadened to work with a variety of products, in which case it falls within the multi-commodity flow problem with which a line of action is decided.
Experiments showed that the optimal solution obtained with the minimum cost flow model changes if the nodes are considered as queueing systems. Another fact observed is that, when the nodes are queuing systems, the optimal solution obtained with the model tends to balance the workload in the nodes and also tends to distribute the flows through the network.
The equations for the properties (WIP and cycle time) are analytic approximations. We observe in the tests that were done that there is a difference between the analytical and simulated results, with the biggest difference being observed in case B3 and the smallest difference being observed in case B4. Even so, we can see that the analytical results have an acceptable level of accuracy.
Under the assumption of Poisson demand, service time exponentianlly distributed and stability of the system, managers and practitionares can expect that the proposed analytical model can be considered as a reliable tool for the analysis of a supply chain.
The conventional minimum cost flow model can be expanded to incorporate elements from queuing networks such as variability of demand, variability of service time, and variability due to failures or set-ups.











 nueva página del texto (beta)
nueva página del texto (beta)