Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nova scientia
versión On-line ISSN 2007-0705
Nova scientia vol.7 no.13 León abr. 2015
Ciencias Naturales e Ingenierías
Transmission properties of Dirac electrons through Cantor monolayer graphene superlattices
Propiedades de transmisión de electrones de Dirac a través de superredes Cantor en grafeno
R. Rodríguez-González1*, J. C. Martínez-Orozco1, J. Madrigal-Melchor1 and I. Rodriguez-Vargas1
1 Unidad Académica de Física, Universidad Autónoma de Zacatecas, México. * E-mail: rodriguezglez.r@fisica.uaz.edu.mx
Recepción: 06-12-2013
Aceptación: 01-07-2014
Abstract
In this work we use the transfer matrix method to study the tunneling of Dirac electrons through aperiodic monolayer graphene superlattices. We consider a graphene sheet deposited on top of slabs of Silicon-Oxide (SiO2) and Silicon-Carbide (SiC) substrates, in which we applied the Cantor's series. We calculate the transmittance for different fundamental parameters such as: starting width, incident energy, incident angle and generation number of the Cantor's series. In this case, the transmittance as function of energy presents self-similar features as a function of the generation number. We also compute the angular distribution of the transmittance for fixed energies finding a self-similar patterns between generations. Finally, we calculate the scaling factor for some transmittance spectra, which effectively show scalability.
Keywords: Graphene, Cantor multilayers, Transmittance, Transfer matrix.
Resumen
En este trabajo usamos el método de la matriz de transferencia para estudiar el tunelamiento de los electrones de Dirac a través de superredes aperiodicas en grafeno. Consideramos una hoja de grafeno depositada encima de bloques de sustratos de Óxido de Silicio (SiO2) y Carburo de Silicio (SiC), en los cuales aplicamos la serie de Cantor. Calculamos la transmitancia para diferentes parámetros fundamentales tales como: ancho de partida, energía de incidencia, ángulo de incidencia y número de generación de la serie de Cantor. En este caso, la transmitancia como función de la energía presenta rasgos autosimilares al variar el número de generación. También computamos la distribución angular de la transmitancia para energías fijas econtrando un patrón autosimilar entre generaciones. Por último, calculamos los factores de escala para algunos espectros de la transmitancia, los cuales efectivamente muestran escalabilidad.
Palabras clave: Grafeno, Multicapas Cantor, Transmitancia, Matriz de transferencia.
1. Introduction:
Graphene a one-atom thick sheet of carbon atoms with hexagonal structure constitutes the basis to build all carbon allotropes: graphite, carbon nanotubes and buckyballs.
From its discovery in 2004 (Novoselov 2004, 666; Novoselov 2005, 197), graphene has attracted a lot of attention due to its unusual properties (Zhang 2005, 201; Katsnelson 2006, 620). Indeed, it brings a natural bridge between solid state physics and quantum electrodynamics, as well as opens a new avenue to possible applications (Schedin 2007, 652; Geim 2007, 183). Much of mentioned comes from its peculiar band structure being a zero bandgap semimetal with linear dispersion relation near to the K point in the Brillouin zone (Wallace 1947, 622), allowing that the electrons behave like relativistic particles even when they move much slower than light, vF = c /300. The results of this odd behavior are unusual effects such as minimum conductivity and Klein tunneling (Zhang 2005, 201; Katsnelson 2006, 620). Effects that from a fundamental perspective are very interesting, and now the opportunity to prove them is superb with graphene. However, from a technological standpoint are not at all advisable since they impede the modulation of the electronic properties of the material.
One possibility to overcome these technological difficulties is to open a bandgap in graphene by means of symmetry-breaking substrates such as SiC and hBN (hexagonal-Boron-Nitride) (Zhou 2007, 770; Giovannetti 2007, 73103). These substrates break the symmetry of the sub-lattices that form the hexagonal structure of graphene creating a bandgap of 0.260 eV and 0.055 eV for SiC and hBN, respectively. Moreover, in the case of SiC (Zhou 2007, 770) the bandgap can be modulated changing the number of graphene layers: 0.144 eV and 0.066 eV for two and three layers, respectively. It is important to mention that materials like SiO2 constitute non-symmetry-breaking substrates preserving the zero bangap properties of graphene.
In this work, we study the transmission properties of Dirac electrons through aperiodic monolayer graphene superlattices. The aperiodic structure is created by alternating symmetry-breaking and non-symmetry-breaking substrates. In particular, we analyze the transmittance of aperiodic structures built according to the substitution rules of the triadic Cantor set.
Method
In the case of symmetry-breaking substrates, are found that the substrates not only generate a bandgap in the graphene spectrum but also change the linear dispersion relation to parabolic (Viana 2008, 325221), see Fig. 1. Moreover, as the electrons in graphene can be treated as relativistic particles hereafter we use the Dirac-like equation given by,
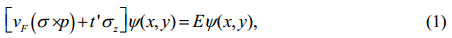
where vF is the Fermi velocity of the Dirac electrons in graphene, t' = mv2F is the mass term, σ= (σx,σy ) are the Pauli matrix, σz is the z component of the Pauli-matrix vector and p = (px, py ) is the in-plane momentum operator. To solve this equation one can writte the following parabolic dispersion relation,

where t' is proportional to the bandgap of value 2t' (we choose t' = 0.10 eV for our numerical results), q is the two-dimensional wave vector associated with the SiC and hBN substrates termed as the q-region (Fig. 1), and "±" states electrons and holes, respectively. The corresponding wavefunctions taken the form,

with the coefficients of the bispinor (Viana 2008, 325221),

qx and qy are the components of the two-dimensional wave vector q.
In the case of non-symmetry-breaking substrates, the linear dispersión relation is conserved and as a consequence not generate a bandgap (Viana 2008, 325221) as is illustrated in Fig. 1. So, the massless Dirac equation can be written as,
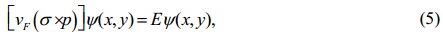
the asocciated energy has the linear form,

with k the two-dimensional wave vectors corresponding to the SiO2 substrate denominated as the k-region (Fig. 1). The wavefunctions are represented by the expression,

with

where s=sign(E and θ= arctan(kx / ky) (Viana 2008, 325221).
It is well known that multiple interface problems can be treated readily by the Transfer Matrix Approach (Yeh 2005). In this sense, the transmission properties of Dirac electrons in multibarrier structures are not the exception. So, if we have a multibarrier structure in which an incident electron with energy E and angle of incidence θ is trying to pass throughout the structure, we can establish a connection between the media to the left and right of the first interface through the continuity conditions of the Dirac equation. To this respect, it is sufficient with the continuity of the wavefunction in each interface of the system, since the Dirac equation is of first order. So, mathematically speaking,

where k (q) states non-symmetry-breaking (symmetry-breaking) substrates and "+" ("-") indicates forward (backward) wave functions. Similar equations can be established for the other interfaces of the multi-interface system resulting in a set of couple equations for the coefficients Ai and Bi. These equations can be solved easily relating the coefficients A0 and B0 of the first region with the coefficients AN and BN of the last region,
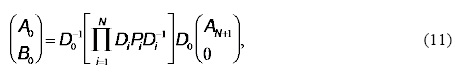
here Diand Pi represent the dynamic and propagation matrices of the i-th layer of the multilayer system, respectively. Defining the transfer matrix of the whole systems as,

we can find the transmittance straightforwardly by the standard formula,

where M11 represents the (1,1) matrix element of the transfer matrix. More details about the
notation and the particular values of the quantities involved can be found in Refs. (Yeh 2005; Viana 2008, 325221).
Results
Our starting system to build the triadic Canto structures is a very thick potential barrier of width "w" and height t'. To us this system represents the first generation, N = 1, of our triadic Cantor graphene structures. So, applying successively the triadic Cantor set rules and appropriately the transfer matrix approach we calculate the transmittance for different combinations of our system parameters: starting width, angle of incidence and Cantor generation. In all our calculations we have maintained the barrier height of the q regions at 0.10 eV. We find self-similar patters in the transmission spectra as a function of the energy and of the angle even when we change the generation.
In Fig. 2 we can see that the transmittance presents small structures in both sides of the point E = 0 that are similar, we have called this apparent similarity "local". The parameters used are w = 540a, N = 3 and θ = (a) 0, (b) π/8, (c) π/4 and (d) 3π/8. Here "a" represents the carbon-carbon distance in graphene. Fig. 3 shows the transmission spectrum for w = 180a and N = 4. In this case we analyzed angles of incidence: (a) 0, (b) π/8, (c) π/4 and (d) 3π/8. The spectra have identical structures, but when we increase the angle of incidence this structure magnified respect to the axis of the energy. A peculiar feature of the transmittance is that it has the same value irrespective of the angle of incidence at E = 0, which means that at this energy the transmittance is determined basically by the effective width of the multilayer structure. For comparison, see Fig. 4 for which the minimum of transmittance at E = 0 is changing according to the generation number, or in other words depending on the effective width of the system.
Fig. 4 represents self-similarity between generations, this is, transmission spectra are quite similar for different numbers of generation. Here, the transmission spectra correspond to w = 540a and θ=/4 for generations (a) N = 3, (b) N = 4, (c) N = 5 and (d) N = 6, respectively. We can notice that the transmission spectra present similar envelopings that nicely obey the well known scaling rules of the triadic Cantor set, see Fig. 6.
We compute the angular distribution of the transmittance finding apparent self-similar patters between different generations. This self-similarity appears when the generations have the same incident energy (Ei) and the same starting width. Fig. 5 displays the transmission spectrum for generations (a) 4, (b) 5 and (c) 6, respectively. The three curves are calculated for the same parameters: w = 1620a and Ei = 75 meV. We can see that the spectra for each case have the same shape.
Finally, we studied the scalability of triadic Cantor multilayers. We have found that the spectrum of all Cantor structures show evident scalability. This is, the total spectrum of a (G, N2) structure appears as a part of a (G, N1) structure, where the scaling factor is: GN2-N with N1>N2. Thus, if we magnify the central part of a (G, N1) structure by the corresponding scaling factor we obtain that the resultant spectrum match up almost perfectly with the spectrum of (G, N2). Here G is the generator and N is the number of generation. Moreover, the period is equal to the total number of peaks that is equivalent to the number of layers (Lavrinenko 2002, 036621). As we can see from Fig. 6 Dirac electrons fulfill with these well known properties.
Conclusions
In summary, we have studied the tunneling properties of Dirac electrons in aperiodic systems based on graphene, particularly the triadic Cantor structures. The system is generated using a single-layer of graphene on alternating substrate, such as SiC and SiO2, which are capable of breaking and no-breaking the symmetry of the graphene structure, or in other words, capable of induce and non-induce a gap, respectively. We have implemented the transfer matrix method to calculate the transmittance for a finite number of barriers arranged according to the triadic Cantor sequence. We have varied some parameters as the starting width, generation number of the sequence, energy and angle of incidence. For the case of the transmittance as function of the energy we obtain that the spectra manifest self-similar characteristic between generations. Moreover, when we choose a starting width and a fixed generation we can see similar structures for both negative and positive energies. On the other hand, self-similar spectra are obtained when we have calculated the angular distribution of the transmittance for different generations. Finally, the scaling factor of the Cantor structures is computed resulting that the transmittance spectra show scalability patterns. In general, we have found that the transmittance spectra of Cantor structures have two fundamental properties: self-similarity and scalability, this as result of the geometrical characteristics of the triadic Cantor sequence.
Acknowledgments
The authors acknowledge the financial support of CONACyT through Grant CB-2010-151713.
References
Geim, A. K., and K. S. Novoselov. 2007. The rise of graphene. Nature Mater. 6:183-191. [ Links ]
Giovannetti, G., P. A. Khomyakov, G. Brocks, P. J. Kelly, and J. van den Brink. 2007. Substrate-induced band gap in graphene on hexagonal boron nitride: Ab initio density functionalcalculations. Phys. Rev. B 76:73103. [ Links ]
Katsnelson, M. I., K. S. Novoselov and A. K. Geim. 2006. Chiral tunneling and the Klein paradox in graphene. Nat. Phys. 2:620-625. [ Links ]
Lavrinenko, A. V., S. V. Zhukovsky, K. S. Sandomirski, and S. V. Gaponenko. 2002. Propagation of classical waves in nonperiodic media: Scaling properties of an optical Cantor filter. Phys. Rev. E 65: 036621. [ Links ]
Novoselov, K. S., A. K. Geim, S. V. Mrozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, and A. A. Firsov. 2004. Electric field effect in atomically thin carbon films. Science 306:666-669. [ Links ]
Novoselov, K. S., A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, and A. A. Firsov. 2005. Two-dimensional gas of massless Dirac fermios in graphene. Nature 438:197-200. [ Links ]
Schedin, F., A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson, and K. S. Novoselov. 2007. Detection of individual gas molecules adsorbed on graphene. Nature Mater. 6:652-655. [ Links ]
Viana Gomes, J. and N. M. R. Peres. 2008. Tunneling of Dirac electrons through spatial regions of finite mass. J. Phys.: Condens. Matter 20: 325221. [ Links ]
Wallace, P. R. 1947. The band theory of graphite. Phys. Rev. 71:622-634. [ Links ]
Yeh, P. 2005. Optical Waves in Layered Media. Wiley-Interscience. [ Links ]
Zhang, Y., Y. -W. Tan, H. L. Stormer, and P. Kim. 2005. Experimental observation of the quantum Hall effect and Berry's phase in graphene. Nature 438:201-204. [ Links ]
Zhou, S. Y., G. -H. Gweon, A. V. Fedorov. P. N. First, W. A. de Heer, D. -H. Lee, F. Guinea, A. H. Castro-Neto, and A. Lanzara. 2007. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 6:770-775. [ Links ]














