Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nova scientia
versión On-line ISSN 2007-0705
Nova scientia vol.7 no.13 León abr. 2015
Ciencias Naturales e Ingenierías
Approximate solutions for HIV-1 infection dynamics with cure rate
Soluciones aproximadas de la dinámica de infección de VIH-1 con tasa de curación
H. Vazquez-Leal1, K. Boubaker2, A. Marin-Hernandez3 y J. Huerta-Chua4
1 Electronic Instrumentation and Atmospheric Sciences School, Universidad Veracruzana, Xalapa, Veracruz, México. E-mail: hvazquez@uv.mx
2 École Supérieure de Sciences et Techniques de Tunis, Université de Tunis, Mahdia, Tunisia.
3 Department of Artificial Intelligence, Universidad Veracruzana, Xalapa, Veracruz, México.
4 Civil Engineering School, Universidad Veracruzana, Poza Rica, Veracruz, México.
Recepción: 09-07-2013
Aceptación: 28-05-2014
Abstract
In this paper, two approximate solutions of HIV-1 infection dynamics model with cure rate are presented. The proposed solutions are obtained using homotopy perturbation method (HPM) and Boubaker Polynomials expansion scheme (BPES). A comparison of obtained solutions shows that HPM and BPES are powerful tools to solve nonlinear host viral infection models.
Keywords: CD4+T cells, Homotopy Perturbation Method, Boubaker Polynomials expansion scheme BPES.
Resumen
En este trabajo, se presentan dos soluciones aproximadas del modelo de la dinámica de infección de VIH-1 con tasa de curación. Las soluciones propuestas se obtienen usando el método de perturbación homotópica, por sus siglas en inglés (HPM) y el esquema de expansión polinomial de Boubaker por sus siglas en inglés (BPES). Al comparar las soluciones obtenidas vemos que HPM y BPES son herramientas muy potentes para resolver modelos no lineales de infecciones virales.
Palabras clave: Células CD4+T, Método de Perturbación Homotópica HPM, esquema de expansión polinomial de Boubaker BPES.
1. Introduction:
In the last three decades, tremendous attention had been paid to establishing mathematical models to Human Immune-deficiency Virus type 1 (HIV-1) proliferation dynamics as AIDS (Acquired Immune Deficiency Syndrome) agent [1-15]. It has been recorded that the main target of HIV-1 infection is the population of CD4+ T-cells, a class of lymphocytes which are abundant white blood immunity cells in plasma.
It is commonly known that HIV-1 targets mainly CD4+ T-cells and causes their death. It decreases the body's ability to fight infections. The standard infection process starts when HIV-1 enters its target T-cell and elaborates DNA copies of its viral RNA, with the help of the reverse transcriptase enzyme RT. Consequently, the viral DNA is inserted into the DNA of the infected cell; which will produce, from itself, viral particles that can bud off the cell and infect other cells.
Throughout the world, already over 16 million deaths at average age of 43 years have been caused by this virus [2-4]; bringing into attention an increasing need to understand and study its action and dynamics. Mathematical models have been proven valuable in understanding the dynamics of HIV infection [4-6].
One of the earliest models to primary infection with HIV is the one developed by Perelson [7], which considered a standard four-population model involving uninfected CD4+ T cells, latently infected CD4+ T cells, productively infected CD4+ T cells, and virus population.
Unfortunately, the models for describing the dynamics of HIV infection for CD4+ cells are usually nonlinear differential equations with no known exact solution. Nonetheless, several methods are focused to find approximate solutions to nonlinear differential equations like: Homotopy perturbation method (HPM) [16-23], variational iteration method (VIM) [24-25], Boubaker Polynomials Expansion Scheme (BPES) [26-33], Homotopy Analysis Method (HAM) [34], Generalized Homotopy Method [35], among many others. Therefore, we propose a comparison between HPM and BPES methods by solving HIV-1 infection dynamics with cure rate [36].
The paper is organized as follows. Section 2 provides an idea about the model and its governing equations. We will describe the basic concepts of HPM in Section 3. Section 4 and Section 5 show the solution procedure for HIV using HPM and BPES, respectively. In Section 6, we discuss the obtained results. Finally, Section 7 summarizes the study and provides a global conclusion.
2. Governing equations and general assumptions
Simple and standard classic models for HIV-1 proliferation dynamics [7,9-15] are generally based on interacting features between three components like: infected and uninfected CD4+ T-cells along with virus population (Fig. 1).
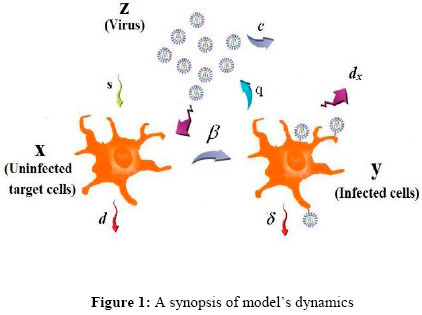
The following equations describe the evolution of the system [36]:
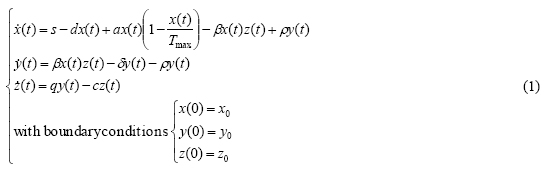
with: x(t) : Uninfected target CD4+T-cells
y(t) : Productively infected CD4+T-cells
z(t) : Viral load of the virons
s : Represents the rate at which new T cells are created from sources
a : Maximum proliferation rate of target cells
Tmax : T population density at which proliferation shuts off
d : Death rate of T cells
β : Infection rate constant
δ : Death rate of infected cells
q : Reproductively rate of the infected cells
c : Clearance rate constant of virions
p : The rate of "cure," i.e. noncytolytic loss of infected cells
The second equation in system (1) traduces anti-retroviral effects in reference to eventual healing effects or entry in eclipse phase. It also expresses that the process of infection to the uninfected CD4+ T-cells is in concordance to the mass action principle under mixing homogeneity. In this case, the concentration of new infected cells is proportional to the product x(t) - y(t).
3. Basic concept of HPM method
The HPM method can be considered as a combination of the classical perturbation technique [37,38] and the homotopy (whose origin is in the topology) [39-40], but not restricted to a small parameter like traditional perturbation methods. For instance, HPM requires neither small parameter nor linearization, but only few iterations to obtain accurate solutions.
To figure out how HPM method works, consider a general nonlinear equation in the form
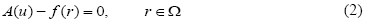
with the following boundary conditions:
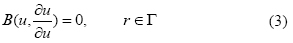
where A is a general differential operator, B is a boundary operator, ƒ (r) a known analytical function, and Γ is the domain boundary for Ω . A can be divided into two operators L and N, where L is linear and N nonlinear; from this last statement, (2) can be rewritten as
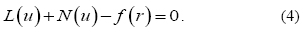
Generally, a homotopy can be constructed in the form [16-18,37]
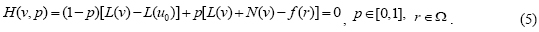
where p is a homotopy parameter whose values are within the range of 0 and 1; u0 is the first approximation for the solution of (4) that satisfies boundary conditions.
When p → 0, (5) is reduced to

where operator L possesses trivial solution.
When p → 1, (5) is reduced to the original problem

Assuming that solution for (5) can be written as a power series of p
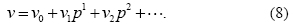
Substituting (8) into (5) and equating identical powers of p terms, there can be found values for the sequence v0, v1, v2,...
When p → 1 in (8), it yields in the approximate solution for (4) in the form
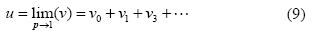
4. Solution by using HPM method
From (1) and (5), we establish the homotopy formulation
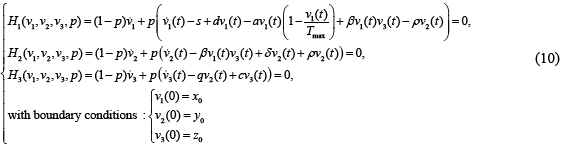
From (8), we assume that solution for (10) can be written as a power series of p as follows

Where vi,j (i= 1,2,3, and j=0,1,2,...), are functions yet to be determined. Substituting (11) into (10), and rearranging the coefficients of p powers, we have
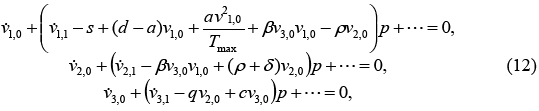
In addition, in order to fulfil the boundary conditions, we consider v1,0(0) = x0, v2,0(0) = y0 and v3,0(0) = z0. In order to obtain the unknown vi,j (i = 1,2,3, and j =1,2,3,...), we must construct and solve the following system of equations, considering initial conditions vi,j (0) = 0 (i =1,2,3, and j =1,2,3,...)
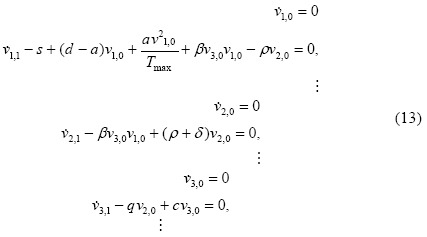
Therefore,
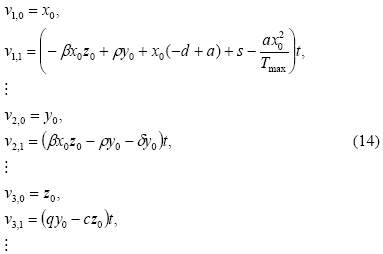
We obtained v1,2,v2,2,v3,2, and succeeding terms; nevertheless, because they were too
cumbersome, we skip them and use only the final results. Then, we obtain the 40-th order approximation, considering p → 1 yields the approximate solution for (1) as
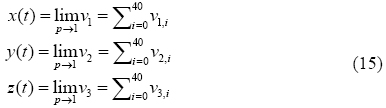
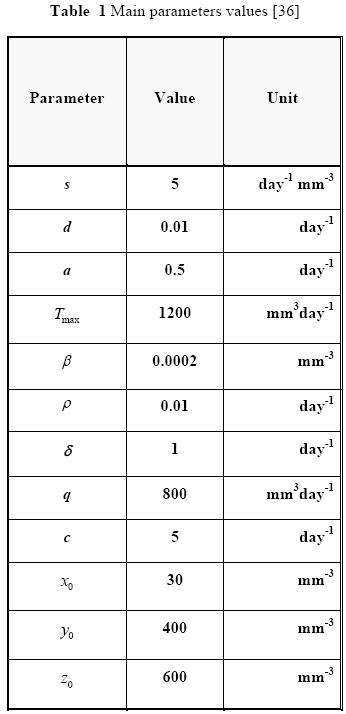
We set the values of parameters and initial conditions (x(0) = x0, y(0) = y0, and z(0) = z0) as reported in Table 1 [41]. In order to increase the domain of convergence, we apply the Padé [20, 35] approximant to (15) and obtain approximations of order x(t)[15/15], y(t )[14/15], and z(t)[14/15].
5. Resolution using the Boubaker Polynomials Expansion Scheme BPES
The resolution of system (1) along with boundary conditions has been achieved using the Boubaker Polynomials Expansion Scheme (BPES) [26-33]. This scheme is a resolution protocol, which has been successfully applied to several applied-physics and mathematics problems. The BPES protocol ensures the validity of the related boundary conditions regardless of main equation features. The protocol uses the Boubaker polynomials first derivatives properties:
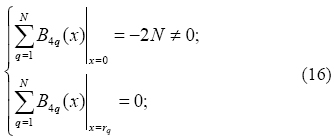
and
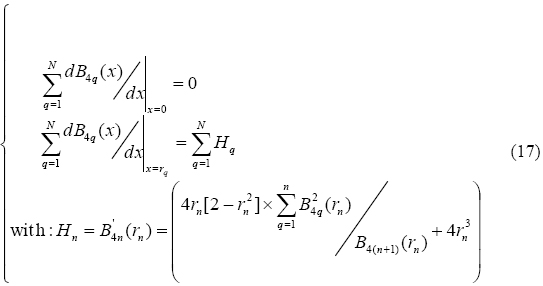
Several solutions have been proposed using BPES in many fields such as numerical analysis, theoretical physics, mathematical algorithms, heat transfer, homodynamic, material characterization, fuzzy systems modelling, and biology [26-33].
The resolution protocol is based on setting 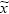 (t),
(t), 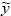 (t), and
(t), and 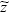 (t) as estimators to the t-dependent variables x(t), y(t), and z(t), respectively
(t) as estimators to the t-dependent variables x(t), y(t), and z(t), respectively
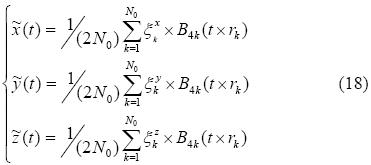
where B4k are the 4k-order Boubaker polynomials [29-30], rk are B4k minimal positive roots, N0 is a prefixed integer, and 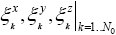 are unknown pondering real coefficients.
are unknown pondering real coefficients.
The main advantage of this formulation is the verification of boundary conditions, expressed in (1), in advance to the resolution process. In fact, thanks to the properties expressed in (16) and (17), these conditions are reduced to the inherently verified linear equations
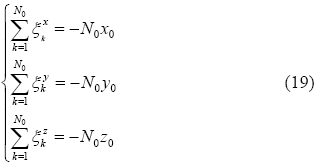
The BPES solution for (1) is obtained, according to the principles of the BPES, by determining the non-null set of coefficients 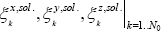 that minimizes the absolute difference between left and right sides of the following equations
that minimizes the absolute difference between left and right sides of the following equations
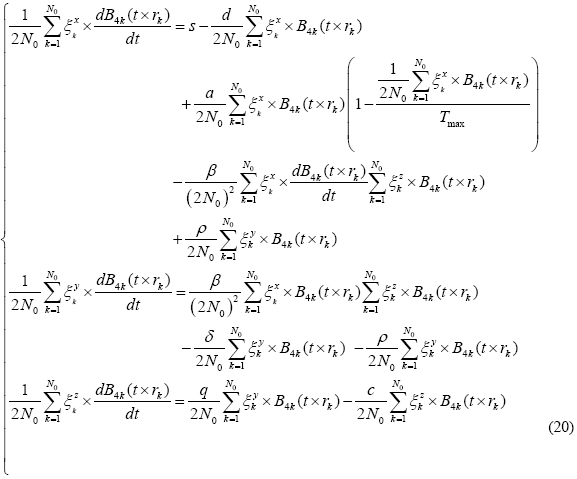
The final solution is
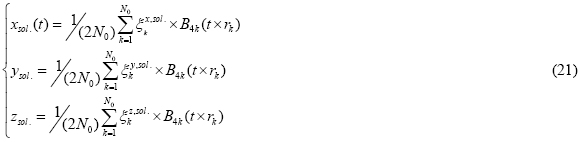
6. Results and analysis
In order to provide a reference point, the obtained results were compared to the numerical solution obtained using the Fehlberg fourth-fifth order Runge-Kutta method with degree four interpolant (RKF45) [42,43] built-in routine from Maple 17 Software. The routine was configured using an absolute error of 10-7 and a relative error of 10-6. Figure 2 through 4 show the graphical comparison of the HPM (15), HPM-Padé and BPES (21) solutions. HPM and BPES solutions exhibit similar domains of convergence; the accuracy of both approximations decrease rapidly for t>0.4 as depicted in figures 2-4 (2,3 y 4). Nonetheless, from the same figures, we can observe that the HPM-Padé solution possesses wider domain of convergence than BPES and standard HPM.
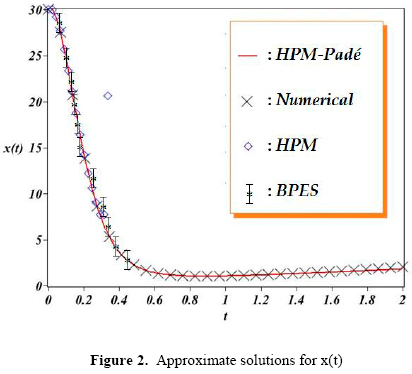
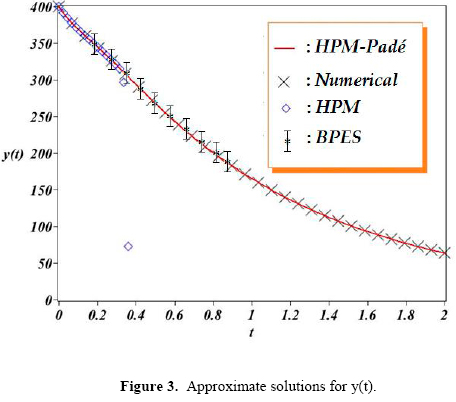
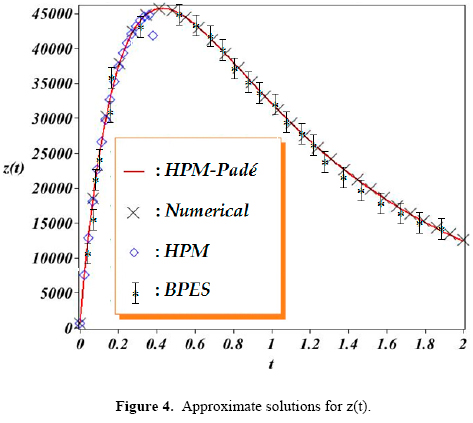
HPM-Padé technique is able to produce easy computable rational expression that exhibit a wide convergence region in comparison to polynomial solutions schemes. Nonetheless, further research is required in order to obtain solutions with even larger domain of convergence that can lead to a better understanding of the dynamics of the HIV infection and its relationship with the parameters of Table 1.
7. Conclusion
In this paper, a comparison of HPM, HPM-Padé and BPES was studied by solving an HIV-1 infection dynamics model with cure rate. The HPM-Padé solution exhibited a wider domain of convergence than HPM and BPES, reaching a good agreement to the exact solution for range t ∈ [o,2]. Further research is required in order to obtain solution with larger domain of convergence that can lead to a better understanding of the dynamics of the HIV infection and the relationship with its parameters.
Acknowledgments
We gratefully acknowledge the financial support provided by the National Council for Science and Technology of Mexico (CONACyT) through grant CB-2010-01 #157024.
References
[1] M. A. Capistran, F. J. Solis, On the modeling of long-term HIV-1 infection dynamics, Mathematical and Comp. Modelling, Vol. 50 (5-6) 777-782, 2009. [ Links ]
[2] R. Xu, Computers & Mathematics with Applications, Global dynamics of an HIV-1 infection model with distributed intracellular delays, Vol. 61(9) 2799-2805, 2011.
[3] R. Xu, Global stability of an HIV-1 infection model with saturation infection and intracellular delay," Journal of Mathematical Analysis and Applications, Vol. 375 (1), 7581, 2011. [ Links ]
[4] L. Rong, A.S. Perelson, J. Theor. Biol., Modeling HIV persistence, the latent reservoir, and viral blips, Vol. 260 308-331, 2009.
[5] S. Ruan, J. Wei, On the zeros of transcendental functions with applications to stability of delay differential equations with two delays, Dyn. of Continuous, Discrete and Impulsive Syst, Vol. 10, 863-874, 2003. [ Links ]
[6] S. Ruan and J. Wei, Periodic solutions of planar systems with two delays, Proc. Royal Soc. Edinburgh Ser. A 129, 1017-1032, 1999. [ Links ]
[7] A.S. Perelson, Modelling viral and immune system dynamics, Nat. Rev. Immunol., Vol. 2 28-36, 2002. [ Links ]
[8] G. Röst, J.Wu, SEIR epidemiological model with varying infectivity and infinite delay, Math. Biosci. and Eng. Vol. 5, 389-402, 2008. [ Links ]
[9] Y. Ding, and H. Ye, A fractional-order differential equation model of HIV infection of CD4+ T-cells, Mathematical and Computer Modelling, Vol. 50(3-4) 386-392, 2009. [ Links ]
[10] K. Wang, W. Wang, H. Pang, X. Liu, Complex dynamic behavior in a viral model with delayed immune response, Physica D, Vol. 226 197-208, 2007. [ Links ]
[11] D. Finzi, M. Hermankova, T. Pierson, L.M. Carruth, C. Buck, R.E. Chaisson, T.C. Quinn, K. Chadwick, J. Margolick, R. Brookmeyer, J. Gallant, M. Markowitz, D.D. Ho, D.D. Richman, R.F. Siliciano, Identification of a Reservoir for HIV-1 in Patients on Highly Active Antiretroviral Therapy, Science Vol. 278 (5341) 1295 -1300, 1997 [ Links ]
[12] P. Nelson, J. Murray, A. Perelson, A model of HIV-1 pathogenesis that includes an intracellular delay, Math. Biosci., Vol. 163 (2) 201-215, 2000. [ Links ]
[13] H. Zhu, X. Zou, Impact of delays in cell infection and virus production on HIV-1 dynamics, Math. Medic. Bio., Vol. 25 (2) 99-112, 2008. [ Links ]
[14] P. Nelson, A. Perelson, Mathematical analysis of delay differential equation models of HIV-1 infection, Math. Bioscien, Vol 179 (1) 73-94, 2002. [ Links ]
[15] J. Tam, Delay effect in a model for virus replication, IMA J. of Math. Applied to Medicine and Biol. Vol. 16(1) 29-37, 1999. [ Links ]
[16] He, J. H., "Homotopy perturbation technique," Comput. Methods Appl. Mech. Eng., Vol.178, 257-262, 1999. [ Links ]
[17] He, J. H., "A coupling method of a homotopy technique and a perturbation technique for non-linear problems," Inter. J. Non-linear Mech., Vol.35, 37-43, 2000. [ Links ]
[18] He, J. H., "Homotopy perturbation method: a new nonlinear analytical technique," Appl. Math. Comput., Vol.135, 73-79, 2003. [ Links ]
[19] H. Vazquez-Leal, Y. Khan, G. Fernández-Anaya, et al., "A General Solution for Troesch's Problem," Mathematical Problems in Engineering, vol. 2012, Article ID 208375, 14 pages, 2012. doi:10.1155/2012/208375. [ Links ]
[20] Hector Vazquez-Leal, Arturo Sarmiento-Reyes, Yasir Khan, Uriel Filobello-Nino, and Alejandro Diaz-Sanchez, "Rational Biparameter Homotopy Perturbation Method and Laplace-Padé Coupled Version," Journal of Applied Mathematics, vol. 2012, Article ID 923975, 21 pages, 2012. doi:10.1155/2012/923975. [ Links ]
[21] Héctor Vazquez-Leal, "Rational Homotopy Perturbation Method," Journal of Applied Mathematics, vol. 2012, Article ID 490342, 14 pages, 2012. doi:10.1155/2012/490342. [ Links ]
[22] Yasir Khan, Hector Vazquez-Leal, and Luis Hernandez-Martinez, "Removal of Noise Oscillation Term Appearing in the Nonlinear Equation Solution," Journal of Applied Mathematics, vol. 2012, Article ID 387365, 9 pages, 2012. doi:10.1155/2012/387365. [ Links ]
[23] Hector Vazquez-Leal, Roberto Castaneda-Sheissa, Uriel Filobello-Nino, Arturo Sarmiento-Reyes, and Jesus Sanchez Orea, "High Accurate Simple Approximation of Normal Distribution Integral," Mathematical Problems in Engineering, vol. 2012, Article ID 124029, 22 pages, 2012. doi:10.1155/2012/124029. [ Links ]
[24] Y. Khan, H. Vázquez-Leal, L. Hernandez-Martinez and N. Faraz, "Variational iteration algorithm-II for solving linear and non-linear ODEs", International Journal of the Physical Sciences Vol. 7(25), pp. 3099-4002, 29 June, 2012. [ Links ]
[25] He, J.H. Variational iteration method-a kind of nonlinear analytical technique: Some examples, International Journal of Nonlinear Mechanics, 1999, 34 (4), 699-708. [ Links ]
[26] M. Agida, A. S. Kumar, A Boubaker Polynomials Expansion Scheme solution to random Love equation in the case of a rational kernel, El. Journal of Theoretical Physics, 2010, 7, 319-326. [ Links ]
[27] J. Ghanouchi, H. Labiadhand K. Boubaker, An attempt to solve the heat transfert equation in a model of pyrolysis spray using 4q-order m-Boubaker polynomials Int. J. of Heat and Technology, 2008, 26, 49-53. [ Links ]
[28] S. Slama, J. Bessrour, K. Boubaker and M. Bouhafs, A dynamical model for investigation of A3 point maximal spatial evolution during resistance spot welding using Boubaker polynomials, Eur. Phys. J. Appl. Phys. 2008, 44, 317-322. [ Links ]
[29] T. Ghrib, K. Boubakerand M. Bouhafs, Investigation of thermal diffusivity-microhardness correlation extended to surface-nitrured steel using Boubaker polynomials expansion, Modern Physics Letters B, 2008, 22, 2893-2907. [ Links ]
[30] A. S. Kumar, An analytical solution to applied mathematics-related Love's equation using the Boubaker Polynomials Expansion Scheme, Journal of the Franklin Institute, 2010, 347, 1755-1761. [ Links ]
[31] S. Fridjine, M. Amlouk, A new parameter: An ABACUS for optimizig functional materials using the Boubaker polynomials expansion scheme, Modern Phys. Lett. B, 2009, 23, 2179-2182. [ Links ]
[32] A. Milgram, The stability of the Boubaker polynomials expansion scheme (BPES)-based solution to Lotka-Volterra problem, J. of Theoretical Biology, 2011, 271, 157-158. [ Links ]
[33] H. Rahmanov, A Solution to the non Linear Korteweg-De-Vries Equation in the Particular Case Dispersion-Adsorption Problem in Porous Media Using the Spectral Boubaker Polynomials Expansion Scheme (BPES), Studies in Nonlinear Sciences, 2011, 2 (1) 46-49. [ Links ]
[34] S. Li, S. Liao, An analytic approach to solve multiple solutions of a strongly nonlinear problem, Applied Mathematics and Computation, 2005, 169, 854-865. [ Links ]
[35] Hector Vazquez-Leal, Generalized homotopy method for solving nonlinear differential equations, Computational and Applied Mathematics, 2013, 14 pages, 10.1007/s40314-013-0060-4. [ Links ]
[36] Xueyong Zhou, Xinyu Song, Xiangyun Shi, A differential equation model of HIV infection of CD4+ T-cells with cure rate, Journal of Mathematical Analysis and Applications, Volume 342, Issue 2, 15 June 2008, Pages 1342-1355, ISSN 0022-247X, 10.1016/j.jmaa.2008.01.008. [ Links ]
[37] Filobello-Nino U, H. Vazquez-Leal, Y. Khan, A. Yildirim, V.M. Jimenez- Fernandez, A.L. Herrera May, R. Castaneda-Sheissa, and J.Cervantes-Perez. Using Perturbation methods and Laplace-Padé approximation to solve nonlinear problems. Miskolc Mathematical Notes, 14 (1) 2013 89-101 e-ISSN: 1787-2413. [ Links ]
[38] Hector Vazquez-Leal, Uriel Filobello-Nino, Ahmet Yildirim, Luis Hernandez-Martinez, Roberto Castaneda-Sheissa, Jesus Sanchez-Orea, J. E. Molinar-Solis and Alejandro Diaz-Sanchez, "Transient and DC approximate expressions for diode circuits", IEICE Electron. Express, Vol. 9, No. 6, pp.522-530, (2012). [ Links ]
[39] Hector Vazquez-Leal, Luis Hernandez-Martinez, Arturo Sarmiento-Reyes, Roberto Castañeda-Sheissa, and Agustín Gallardo-Del-Angel, "Homotopy method with a formal stop criterion applied to circuit simulation", IEICE Electron. Express, Vol. 8, No. 21, pp.1808-1815, 2011. DOI: 10.1587/elex.8.1808. [ Links ]
[40] Hector Vazquez-Leal, Luis Hernandez-Martinez, and Arturo Sarmiento-Reyes, "Double-Bounded Homotopy for analysing nonlinear resistive circuits", International Symposium on Circuits and Systems, Kobe, Japon, 2005pp. 3203- 3206. [ Links ]
[41] Hector Vazquez-Leal, Luis Hernandez-Martinez, and Arturo Sarmiento-Reyes, and Roberto Castañeda-Sheissa, "Numerical continuation scheme for tracing the double bounded homotopy for analysing nonlinear circuits", International Conference on Communications, Circuits and Systems, Hong Kong, China, 2005,pp. 1122- 1126. [ Links ]
[42] Enright, W.H.; Jackson, K.R.; Norsett, S.P. abd; Thomsen, P.G. Interpolants for Runge-Kutta Formulas. ACM TOMS, Vol. 12, pp. 193-218, 1986. [ Links ]
[43] Fehlberg, E. Klassische Runge-Kutta-Formeln vierter und niedrigerer Ordnung mit Schrittweiten-Kontrolle und ihre Anwendung auf Waermeleitungsprobleme. Computing, Vol. 6, pp. 61-71, 1970. [ Links ]














