Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Nova scientia
versão On-line ISSN 2007-0705
Nova scientia vol.6 no.12 León Out. 2014
Ciencias Naturales e Ingenierías
Osciladores Caóticos implementados en Microcontrolador PIC18F
Chaotic Oscillators implemented into a PIC18F Microcontroller
R. Chiu 1,2, M. Mora-González 2 y D. López-Mancilla 2
1 Facultad de Ingeniería en Computación y Electrónica, Universidad De La Salle Bajío
2 Departamento de Ciencias Exactas y Tecnología, Centro Universitario de los Lagos, Universidad de Guadalajara, Lagos de Moreno, México
R. Chiu. E-mail: rchiu@culagos.udg.mx
Recepción: 17-06-2013
Aceptación: 04-12-2013
Resumen
Introducción: Recientemente, los sistemas caóticos han llamado la atención de la comunidad científica internacional, debido a sus potenciales aplicaciones en varias ramas de la ciencia e ingeniería. Se han propuesto muchos trabajos con el fin de resolver algunos problemas interesantes, como la determinación de daños estructurales en los materiales o en sistemas de comunicaciones seguras. Sin embargo, la mayoría de estos trabajos se enfocan en sistemas caóticos en tiempo continuo, mientras que en muchos casos, es deseable que estos sistemas estén en el modo de tiempo discreto y puedan ser utilizados en tiempo real.
Método: El presente trabajo propone la implementación experimental de tres osciladores caóticos discretizados en un microcontrolador simple. Los osciladores caóticos a implementar son muy conocidos y muy utilizados para ejemplificar posibles soluciones a diversos problemas: los osciladores de Lorenz, Rössler y Chen. Para lo cual, se utilizan tan solo un microcontrolador de bajo costo, unos cuantos resistores y un algoritmo de computación sencillo.
Resultados: Se obtiene un sistema embebido de bajo costo y sencillo para implementar osciladores caóticos discretizados.
Discusión o Conclusión: Se demuestra que los osciladores caóticos de Lorenz, Rössler y Chen pueden implementarse en cualquier microcontrolador de arquitectura basada en palabras de 18 bits o más. Además, se observa que el algoritmo propuesto se pude migrar de un oscilador a otro con solo sustituir el sistema caótico de ecuaciones.
Palabras Clave: Sistemas caóticos en tiempo discreto, microcontroladores, sistema de Lorenz, ecuaciones de Chen; sistema de Rössler
Abstract
Introduction: Chaotic systems are of great interest in various branches of science and engineering. Many works have been proposed in order to solve some different interesting problems, such that determining structural damages in materials or for secure communications systems. However, several approaches are in continuous-time, whereas in many cases, the systems are desired to be in discrete-time mode and in real time.
Method: In this work, an experimental implementation of three chaotic oscillators into a simple microcontroller is proposed. The chaotic oscillators to implement are Lorenz, Rössler and Chen. The implementation consists only of a low cost microcontroller, a few resistors and a simple algorithm.
Results: An inexpensive and simple embedded system to generate chaotic oscillators was obtained.
Discussion or Conclusion: The implementation of chaotic oscillators of Lorenz, Rössler and Chen into 18 bits microcontroller is demostrated. It is further noted that the proposed algorithm could migrate from one oscillator to another with only replace chaotic system equations.
Keywords: Discrete-time chaotic systems, Microcontrollers, Lorenz system, Chen's equations, Rössler system.
Introducción
Desde que los pioneros Pecora y Carroll reportaron en 1990 las posibles aplicaciones de la sincronización de sistemas caóticos, estas han despertado el interés de la comunidad internacional por su utilidad en muchos campos de la ciencia y la ingeniería, como en sistemas biológicos, reacciones químicas, comunicaciones seguras y evaluación de daños estructurales, por mencionar algunas de ellas (Pecora y Carroll, 1990; G. Chen y X. Dong, 1998; Kuomo et al, 1993; Moniz et al., 2005; Moniz et al., 2004; Jiang et al, 2003). Desde entonces, la aplicación más común ha sido en sistemas de comunicaciones seguras. Las comunicaciones basadas en caos requieren, en la mayoría de los casos, de sincronización de sistemas caóticos, ya sea estructuralmente idénticos o diferentes, bajo ciertas condiciones. Debido a que los sistemas caóticos son extremadamente sensibles a condiciones iniciales, es decir, que condiciones iniciales ligeramente diferentes generan trayectorias completamente diferentes a largo plazo, generalmente se requieren algoritmos de control para lograr sincronización en sistemas caóticos acoplados unidireccionalmente. Una vez sincronizados, es posible encriptar un mensaje mediante una señal portadora caótica desde un transmisor, de tal forma que esta no sea recuperada por intrusos, pero que pueda ser recuperada fielmente por el destinatario en un receptor adecuado que permita remover la señal portadora caótica (ej. Kocarev, 1992). Muchos trabajos han sido desarrollados bajo esta propuesta para encriptar señales de audio y señales digitales, incluyendo imágenes (López-Mancilla y Cruz-Hernández, 2005a, 2005b; López-Gutiérrez et al., 2009; García-López et al., 2008; López-Mancilla et al., 2005; Larger y Goedgebuer, 2004; Inzunza y Cruz, 2013).
La sincronización de sistemas caóticos y sus aplicaciones potenciales, ha dirigido su atención desde el inicio, a la implementación de sistemas caóticos analógicos y discretos. Los analógicos, generalmente, se implementan en circuitería electrónica analógica, mientras que los discretos pueden implementarse en microcontroladores o sistemas digitales (Cruz-Hernández et al, 2005; Tanougast, 2011; Tanougast et al, 2012; Sadoudi, 2009). Sin embargo, la mayoría de los trabajos existentes se enfocan en circuitos caóticos analógicos o simulaciones numéricas en computadoras de sistemas caóticos en tiempo continuo, y existen pocos trabajos que exploran la posibilidad de encapsular un sistema caótico en un microcontrolador o un Arreglo de Compuertas Programable en Campo (FPGA, por sus siglas en inglés). Las simulaciones en computadoras no permiten extraer los datos a través de un puerto de manera directa, a no ser que se utilice una tarjeta Convertidor Digital-Analógico (DAC, por sus siglas en inglés) o un puerto de datos. Es decir, se requiere de hardware adicional. Dado lo anterior, puede ser ventajoso tener un sistema caótico o varios de ellos, embebidos en un componente pequeño del cual se pueda disponer de los estados de estos sistemas para propósitos de sincronización o control de los mismos, funcionando como una planta caótica física y que esto pueda ser utilizado en un sistema de comunicaciones inalámbricas seguras, o en sistemas de seguridad electrónicos: como controles de puertas eléctricas, o alarmas seguras de autos o de casa habitación. Note que la ventaja de tener uno o varios sistemas embebidos en un solo microcontrolador sobre tener uno o varios sistemas analógicos en circuitería electrónica analógica es principalmente el tamaño o la portabilidad de los mismos.
Con este propósito, en el presente trabajo se aborda la implementación del sistema caótico de Lorenz, discretizado en un microcontrolador simple. El sistema se compone tan sólo de un microcontrolador de bajo costo, además de un arreglo resistivo que actúa como DAC. Dado que el microcontrolador se puede programar en lenguaje C, el programa puede ser fácilmente reconfigurable, y con esto el sistema puede migrar en distintos sistemas caóticos, por ejemplo Rössler y Chen. Por lo cual, en el presente trabajo también se ejemplifica la implementación de estos dos últimos sistemas caóticos.
Método
En 1963 Edward Norton Lorenz publicó su famoso conjunto de ecuaciones diferenciales ordinarias, no lineales, de primer orden (Lorenz, 1963); estas son relativamente simples, pero su comportamiento resulta asombrosamente complejo. Desde un punto de vista técnico el sistema de Lorenz es un sistema no lineal, tridimensional y determinista. Las ecuaciones de Lorenz son quizás unas de las ecuaciones más estudiadas dentro del campo de los sistemas no lineales. Esta es la razón por la cual escogimos este sistema de ecuaciones para implementarlas en el microcontrolador PIC18F4550. Las ecuaciones normalizadas de Lorenz están dadas por
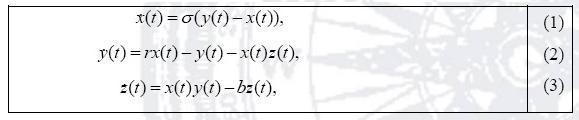
donde x(t), y(t) y z(t) son los estados del sistema y los valores de parámetros necesarios para expresar un comportamiento caótico son = 10, b = 8/3, y r = 28. El parámetro crítico, también conocido como parámetro Rayleigh es r.
Con la finalidad de implementar el oscilador en el microcontrolador, se utilizó el sistema de Lorenz en tiempo discreto, para esto se aplicó el método de Euler a las ecuaciones (1-3). La mayoría opta por discretizar sistemas continuos usando el método de Runge-Kutta, de tercer o cuatro orden, debido a que es más exacto al hacer el cómputo repedidas veces sobre los resultados obtenidos. Sin embargo, en este trabajo, se elige el método de Euler por ser muy fácil de utilizar, principalmente para aquellos que inician con procesos de discretización, y porque permite obtener la solución deseada si necesidad de gran exactitud. Así mismo, al ser un algoritmo de fácil aplicación, permite al microcontrolador tener una mayor velocidad de procesamiento, mientras que con Runge-Kutta puede existir una mayor complejidad de cómputo. Por otra parte, presenta la ventaja de que, con tan solo cambiar tres líneas en el algoritmo y modificando parámetros y condiciones iniciales, se puede cambiar el sistema caótico, lo que no ocurre con métodos más complejos. Algunos trabajos ya han sido reportados usando el método de Runge-Kutta, implementados en FPGA's y con lenguaje de programación VHDL (Tanougast, 2011; Tanougast et al, 2012; Sadoudi, 2009). En este trabajo se utiliza un microprocesador de 16 bits y lenguaje C para programarlo, que ofrece como ventajas, con respecto a los trabajos citados, un tamaño reducido, un menor costo y mayor simplicidad de implementación y programación. Aplicando entonces el método de Euler, se obtiene como resultado el siguiente sistema de ecuaciones en diferencias

Aquí X(k),Y(k), y Z(k) conforman el estado del sistema en tiempo discreto, donde los parámetros utilizados en el sistema de ecuaciones anterior son las mismas a excepción del parámetro ts, que es el período de muestreo. El período de muestreo ts debe ser tal que ts = 0.1/ǀλǀmax (Haugen, 2004). Computando la expresión para los valores propios dada por (Lorenz, 1963), se obtiene la el valor ǀλǀmax = 22.8277. Por lo tanto, el período de muestreo cumple con ts = 0.00438.
La figura 1 muestra el circuito electrónico empleado para implementar el oscilador de Lorenz. Se utilizó un microcontrolador PIC18F4550 de Microchip®, donde los puertos B y D del microcontrolador fueron acoplados a una red resistiva en escalera R-2R, la cual hace las veces de un DAC. Este arreglo microcontrolador y DAC R-2R fue seleccionado debido a que es un arreglo económico y de configuración muy simple. Las salidas del DAC se tomaron de las resistencias etiquetadas como R9 y R28, que corresponden a las salidas x(t) y z(t) del oscilador de Lorenz, respectivamente. Nótese que las salidas del sistema son analógicas después de la red resistiva en escalera, pero es posible tomar la salida en modo discreto.
Para probar el arreglo, el código en lenguaje C mostrado en la tabla 1, fue implementado utilizando el compilador C18 de Microchip®, el resultado de las variables X(k) y Z(k) fueron direccionadas de los puertos B y D del microcontrolador, para luego ser convertidas a voltaje analógico por medio del DAC R-2R, por lo cual como salidas resultantes se obtienen a x(t) y z(t). Las líneas 1 a la 13 fueron utilizadas para configurar el microcontrolador en su modo de operación. De la línea 16 a la 19 se declararon las constantes σ, b y r, así como también se inicializó el tiempo de muestreo ts del sistema de Lorenz. Las condiciones iniciales se declararon de las líneas 23 a la 25. Las salidas X(k), Y(k) y Z(k) fueron declaradas en la línea 27. Las instrucciones TRISB y TRISD se utilizan para configurar como salida digital a los puertos B y D, respectivamente. Después de calcular las ecuaciones, los resultados se envían a los puertos B y D.
Los voltajes de salida fueron digitalizados a través de un osciloscopio Tektronics® series 2000; los datos fueron almacenados en un archivo txt para manipulación futura. En la figura 2, se muestra la captura de pantalla del osciloscopio conectado al microcontrolador.
Para implementar otro tipo de oscilador caótico en el mismo arreglo electrónico, solo se deben intercambiar las ecuaciones de estado por las del nuevo oscilador. Por ejemplo, el sistema en ecuaciones de estado en tiempo continuo del oscilador Rössler es

donde los parámetros característicos tienen los valores a = b = 0.2 y c = 5.7, esto con la finalidad de que el sistema de Rössler exhiba comportamiento caótico. Al igual que en el sistema de Lorenz, se obtienen el sistema de ecuaciones en tiempo discreto para el oscilador de Rössler, que son

Análogamente, es sistema oscilador caótico de Chen se implementa con el siguiente sistema de ecuaciones de estado en tiempo continuo
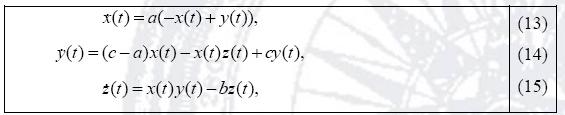
donde los parámetros característicos tienen los siguientes valores a = 35, b = 3 y c = 28, esto con la finalidad de obtener oscilaciones caóticas. Al igual que en los sistemas anteriores, se obtienen el sistema de ecuaciones en tiempo discreto para el oscilador de Chen, el cual es
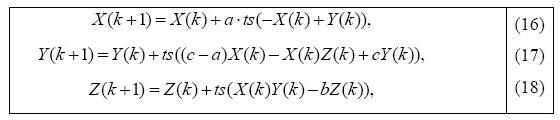
donde se puede observar que las variables de estado z(t) en los osciladores de Lorenz y Chen son iguales, esto es las ecuaciones (3 y 6) son iguales a las ecuaciones (15 y 18), esto debido a que el oscilador de Chen es una variante de las ecuaciones de Lorenz. El tiempo de muestreo utilizado en estos dos últimos osciladores fue el mismo que el utilizado en el oscilador de Lorenz.
Para programar en lenguaje C las ecuaciones de Rössler (7-12) y las ecuaciones de Chen (13-18), solo hay que hacer unas pequeñas modificaciones en el programa original de la Tabla 1, las líneas a modificar son las de las de los parámetros que aparecen en el algoritmo como "constantes" (líneas 16-18), las de las condiciones iniciales (líneas 23-25), así como las de las ecuaciones de estado (líneas 32-34). En la tabla 2, se tienen dichas líneas de código para ambos osciladores (Rössler y Chen). Cabe hacer mención que se sugiere modificar las líneas de condiciones iniciales y constantes, ya que los diferentes osciladores caóticos oscilan con diferentes condiciones de parámetros, y las sugeridas en la Tabla 2 son condiciones normales de operación para estos tipos de osciladores.
Las condiciones iniciales con las cuales inician los tres osciladores (x1, y1, z1) utilizadas en las líneas (23-25) de los códigos de las tablas 1 y 2, se escogieron arbitrariamente, solo cuidando que las tres no sean cero, para que existan oscilaciones, y que no sean demasiado grandes para no inestabilizar a los sistemas.
Resultados y Discusiones
En la figura 3 se muestran los diagramas de bifurcación, para los sistemas en tiempo continuo (izquierda) y en tiempo discreto (derecha), donde el parámetro r es variado desde un valor 16 hasta un valor 200. En estos diagramas se puede observar que, aunque el sistema discretizado no tiene una dinámica idéntica al sistema en tiempo continuo, es decir, aunque siguen trayectorias diferentes, el sistema discretizado sigue representando una dinámica de Lorenz. Esto es importante recalcarlo, porque no es el interés de este trabajo sincronizar la dinámica discreta con la continua, sino más bien, generar dinámicas discretas del sistema de Lorenz para ser implementadas en un microcontrolador de manera muy simple.
Así, este resultado muestra que el sistema propuesto puede reproducir toda la dinámica involucrada en el sistema de Lorenz.
El período de muestreo afecta la estabilidad y la dinámica en el proceso de discretización. Si bien es cierto que se calculó el período de muestreo para ser ts = 0.00438, variaciones en este valor pueden generar un efecto adverso en la discretización como se muestra en la figura 5, donde se puede observar que si se elige un valor muy pequeño ts = 0.0001, se requirirá de una ventana de tiempo muy grande para observar las osciladiones, como se muestra en los incisos a): ts = 0.0001 y b): ts = 0.0012, de tal forma que no se aprecia la dinámica caótica del sistema.
A medida que el valor ts se incrementa, el sistema empieza a oscilar, cada vez con mayor dinámica, hasta alcanzar una solución muy conocida correspondiente a la señal temporal de Lorenz, como en c): ts = 0.0033, d): ts = 0.0064 ó e): ts = 0.0105. Pero si ts se incrementa por encima de 0.015, existe un solapamiento o aliasing de la señal, haciendo que se pierdan datos del sistema analógico, como ocurre en los incisos f): ts = 0.0156 y g): ts = 0.0217. Este solapamiento puede hacer que la discretización se inestabilice, debido a pendientes muy abruptas de la forma de onda muestreada, como se muestra en h): ts = 0.0288 e i): ts = 0.0369.
Se puede corroborar lo que pasa recurriendo al diagrama de bifurcación calculado para la variación de ts, mientras que todos los parámetros de Lorenz permanecen constantes. La figura 5, muestra el diagrama de bifurcación que que ejemplifica la variación de la dinámica obtenida en el muestreo del sistema discreto de Lorenz en función del período de muestreo ts. Note que cuando ts = 0.0001, la dinámica del sistema es pobre en contenido frecuencial, y por tanto oscila lentamente. A medida que ts se incrementa, el sistema oscila en régimen caótico y cuando pasa un umbral de aproximadamente ts = 0.022, el proceso de muestreo no reproduce la señal analógica.
Además, dada la simplicidad del algoritmo, se pueden implementar distintos sistemas caóticos con tan solo cambiar las ecuaciones dentro del código del microcontrolador (ver tabla 2). En la figura 6 (a y b) se observan las evoluciones temporales utilizadas para generar los osciladores caóticos de Rössler y Chen, respectivamente. Para los cuales en la figura 6(a) se muestra el atractor del oscilador Rössler, así como en la figura 7(b) se muestra el atractor del oscilador Chen. También se graficaron los diagramas de bifurcación para estos otros dos osciladores caóticos, en la figura 8(a) se observa el diagrama de bifurcación de Rössler, así como en la figura 8(b) se observa el de Chen.
Los beneficios de implementar los osciladores en un microcontrolador es que cada oscilador caótico trabaja en forma digital y se puede simplificar el desarrollo de los osciladores utilizando un microcontrolador, haciendo que el circuito físico se tenga en forma compacta. Al ser un algoritmo computacional, no habrá problemas con variaciones en los parámetros, ruido inducido o perturbaciones externas que afecten el desempeño de los osciladores. Además se puede tener más de un oscilador a la vez y se pueden utilizar para diversos propósitos.
Conclusiones
En este trabajo se ha mostrado que es posible implementar un oscilador caótico en un sencillo microcontrolador, utilizando un algoritmo simple. Esto mediante la aplicación de las ecuaciones de tres osciladores caóticos comunes en tiempo discreto: Lorenz, Rössler y Chen. Nuestros resultados muestran que el comportamiento de los sistemas propuestos es de acuerdo con los reportados en la literatura. El algoritmo propuesto abre la posibilidad de utilizar sistemas caóticos embebidos en un chip que permita aplicaciones prácticas, en sistemas de comunicaciones inalámbricas seguras, o en alarmas de seguridad en autos o casa habitación.
Se mostró la versatilidad del algoritmo y hardware propuestos, al poder migrar entre cualquiera de los tres sistemas caóticos sugeridos de manera sencilla, ya que solo hay que cambiar pocas líneas de código en el programa en lenguaje C para implementar cualquiera de los tres sistemas caóticos.
Como trabajo a futuro queda la aplicación de los sistemas complejos, por ejemplo, el acoplamiento de maestro y esclavo sistemas caóticos, donde se puede estudiar el problema de la sincronización en tiempo real.
Agradecimientos
El presente trabajo fue apoyado por la Universidad de la Salle Bajío, en beca de investigación de la "9a convocatoria de Investigadores en consolidación" y por el proyecto de Ciencia Básica del Conacyt No. 166654.
Referencias
[1] L. M. Pecora and T. L. Carroll. "Synchronization in chaotic systems," Phys. Rev. Lett. 64, 1990, pp. 821-824. [ Links ]
[2] G. Chen and X. Dong, From Chaos To Order, World Scientific, Singapore. 1998. [ Links ]
[3] K.M. Cuomo, A.V. Oppenheim and S.H. Strogratz, "Synchronization of Lorenz-based chaotic circuits with applications to communications," IEEE Trans. Circuits Syst. II, 40(10), 1993, pp. 626-633. [ Links ]
[4] Moniz, L., Nichols, J.M., Nichols, C.J., Seaver, M., Trickey, S.T., Todd, M.D. Pecora, L.M. and Virgin, L.N. (2005). A multivariate, attractor-based approach to structural health monitoring. Journal of Soundand Vibration 283(1): 295-310. [ Links ]
[5] Moniz, L., Pecora, L., Nichols, J., Todd, M. and Wait, J.R. (2004). Dynamical assessment of structural damage using the continuity statistic. Structural Health Monitoring 3(3): 199-212. [ Links ]
[6] Jiang, G.P., Tang, W.K.S. and Chen, G. (2003). A simple global synchronization criterion for coupled chaotic systems. Chaos, Solitons and Fractals 15(1): 925-935. [ Links ]
[7] L. Kocarev, K.S. Halle, K. Eckert and L. O. Chua, "Experimental demostration of secure communications via chaotic synchronization," Int. J. Bifurc. Chaos, 2(3), 1992, pp. 709-713. [ Links ]
[8] López-Mancilla, D. y Cruz-Hernández, C. (2005b). Output synchronization of chaotic systems: model-matching approach with applications to secure communications. Nonlinear Dynamics and Systems Theory: An International Journal of Research and Survey, 5(2): 141-156. [ Links ]
[9] López-Gutiérrez, R.M., Posadas-Castillo, C., López-Mancilla, D. y Cruz-Hernández, C. (2009). Communicating via robust synchronization of chaotic lasers. Chaos, Solitons & Fractals, 42: 277-285. [ Links ]
[10] García-López, J.H. Jaimes-Reátegui, R. Chiu-Zarate, R. López-Mancilla, D. Ramírez-Jiménez R. y Pisarchik A.N. (2008). Secure computer communication based on chaotic Rössler oscillators. The open Electrical and Electronic Engineering Journal, 2: 24-27. [ Links ]
[11] Cruz-Hernández, C. López-Mancilla, D. García, V. Serrano H. y Núñez R. (2005). Experimental realization of binary signals transmission using chaos. Journal of Circuits, Systems and Computers, 14(3): 1-16. [ Links ]
[12] Larger, L. and Goedgebuer, J.P. (2004). Encryption using chaotic dynamics for optical telecommunications. C. R. Physique 5(1): 609-611. [ Links ]
[13] Inzunza-González, E. y Cruz-Hernández, C. (2013). Double encryption for security in biometric systems. Nonlinear Dynamics and Sistems Theory: An International Journal of Research and Survey, 13(1): 55-68. [ Links ]
[14] Camel Tanougast, Hardware Implementation of Chaos Based Cipher: Design of Embedded Systems for Security Applications, Chaos-Based Cryptography Studies in Computational Intelligence Volume 354, 2011, pp 297-330. [ Links ]
[15] Camel Tanougast, Abbas Dandache, Mohamed Salah Azzaz and Said Sadoudi (2012). Hardware Design of Embedded Systems for Security Applications, Embedded Systems - High Performance Systems, Applications and Projects, Dr. Kiyofumi Tanaka (Ed.), ISBN: 978-953-51-0350-9, InTech, Available from: http://www.intechopen.com/books/embedded-systems-high-performance-systems-applications-andprojects/hardware-design-of-embedded-systems-for-security-applications. [ Links ]
[16] Said Sadoudi ¤, Mohamed Salah Azzaz, Mustapha Djeddou, Mustapha Benssalah, An FPGA Real-time Implementation of the Chen's Chaotic System for Securing Chaotic Communications, International Journal of Nonlinear Science Vol.7(2009) No.4,pp.467-474. [ Links ]
[17] Finn Haugen, (2004) Model Forms and Time-Response Calculations. en Dynamic Systems: Modeling, Analysis And Simulation, 50-73, Tapir Academic [ Links ]
[18] Lorenz, Edward Norton. (1963). Deterministic nonperiodic flow. Journal of the Atmospheric Sciences 20(2): 130–141. [ Links ]
[19] Rössler, O.E. (1976). An equation for continuous chaos. Phys. Letters, 57A(5): 397-398. [ Links ]
[20] Chen, G. y Ueta, T. (1999). Yet another chaotic attractor. Int. J. Bifur. Chaos, 9: 1465–1466. [ Links ]














