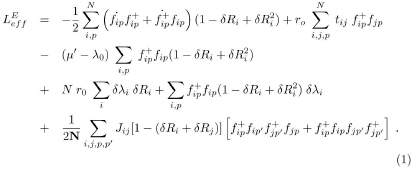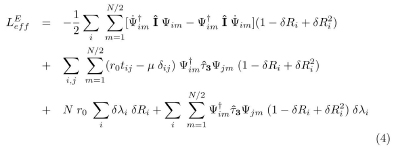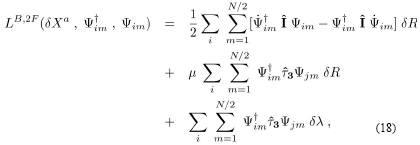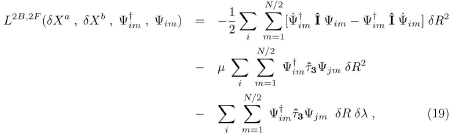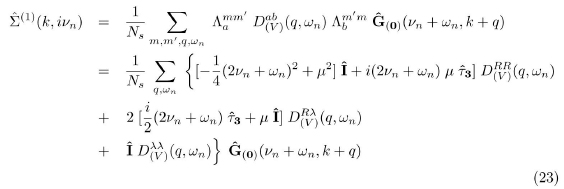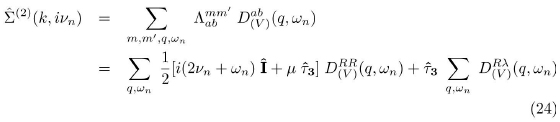Ciencias Naturales e Ingenierías

 

Non perturbative expansion for the Generalized Hubbard Model

 

Desarrollo No Perturbativo para el Modelo de Hubbard Generalizado

 

Oscar P. Zandron

 

Facultad de Ciencias Exactas, Ingeniería y Agrimensura de la Universidad Nacional de Rosario. Argentina. E-Mail: ozandron@ifir-conicet.gov.ar

Consejo Nacional de Investigaciones Científicas y Técnicas, Argentina.

 

Recepción: 11-03-10 
Aceptación: 07-05-10

 

Abstract

In this paper we extend previous results obtained in the framework of the Lagrangian formalism for the normal-state case to the superconducting state. The non-perturbative expansion applied to the generalized Hubbard model describing N-fold-degenerate correlated bands for large-N is considered. The standard Feynman diagrammatics is obtained and the renormalized physical quantities for this model are computed and analyzed. Our purpose is to obtain the 1/N corrections to the renormalized boson and fermion propagators for a state with Cooper-pair condensation.

Keywords: Lagrangian formalism, Hubbard model, Feynman diagrammatics.

 

Resumen

Se extienden a un estado superconductor nuestros resultados previamente obtenidos para un estado normal en el marco del formalismo Lagrangiano. Se considera la expansión no-perturbativa a N grande aplicada a un modelo generalizado de Hubbard describiendo N bandas degeneradas correlacionadas. Se obtienen la diagramática Feynman del modelo y se calculan y analizan las cantidades físicas renormalizadas. Nuestro propósito es obtener la corrección 1/N de los propagadores bosónico y fermiónico renormalizados cuando se tiene en cuenta un estado de condensación de pares de Cooper.

Palabras claves: Lagrangiano, Modelo de Hubbard, Diagramática de Feynman.

 

1. Introduction

Many problems concerning the superconductivity of strongly correlated systems within the context of the generalized Hubbard model were treated by using the decoupled slave-boson representation (Kotliar and Liu 1988, 5142; Grilli and Kotliar 1990, 1170 and Tandon, Wang and Kotliar 1999, 2046) [1, 2]. In this papers, the generalized Hubbard model describing N-fold-degenerate correlated bands in the infinite-U limit by means of the large-N expansion was studied. From slave-boson techniques, thus it contributes to the dynamics of fermion, Fermi-liquid properties of strongly correlated systems were studied. In turn, it is shown that the 1/N corrections give rise to different superconducting instabilities according to the band structure and the filling factor.

As it is known, the slave-particle models exhibit a local gauge invariance which is destroyed in the mean field approximation. This local gauge invariance has associated a first class constraint which is difficult to handle in the path-integral formalism.

The Hubbard operator representation naturally allows to study the electronic effects (Izyumov 1997, 445 and Coleman, Hopkinson and Pépin 2001, 140) [3, 4], we have developed a Lagrangian formalism whose Lagrangian is written in terms of the Hubbard X-operators. So, the field variables are directly the Hubbard X-operators (Foussats, Greco and Zandron 1999, 238; Foussats, Greco, Repetto, Zandron and Zandron 2000, 5849; Foussats, Repetto, Zandron and Zandron 2002, 1053 and Abecasis and Zandron 2007, 1861) [5, 6, 7, 8]. In this approach, the Hubbard X-operators representing the real physical excitations are treated as indivisible objects and no decoupling scheme is used.

Next, by using the path-integral technique, the correlation generating functional and the effective Lagrangian were constructed. This is the quantization of the model by constructing the standard Feynman diagrammatics in terms of the Hubbard X-operators.

Later on, in Ref. [7] the quantization of the t-J model in terms of the Hubbard X-operators for the normal state was given. The non-perturbative formalism for the generalized Hubbard model was analyzed. This was done by means of a new large-N expansion in the infinite-U limit carried out on our Lagrangian formalism for the t-J model. The parameter N represent the number of the electronic degrees of freedom per site and 1/N can be considered as a small parameter.

Thus, defining proper propagators and vertices the standard Feynman diagrammatics of the model is given, so, the bosonic and the fermionic self-energies can be renormalized. From these renormalized quantities several physical properties can be evaluated and the results were confronted with others previously obtained. The free boson propagator, of order 1/N, is renormalized by series of fermionic bubbles whose contributions are also of order 1/N. In relation to these problems it is therefore important to take into account previous results for the Hubbard model describing dipolar bosons in optical lattices (Liang, Liang and Liu 2003, 436 and Xie and Liu 2004, 456) [9, 10].

The generalized Lagrangian model was checked by explicit computation of charge-charge and spin-spin correlation functions (Foussats and Greco 2002, 1951) [11]. The agreement with previous results is excellent and gives a strong test of our Lagrangian approach as well as of the large-N expansion.

Using the Dyson equation the renormalized fermionic propagator can be evaluated at order 1/N by solving the correspondent equations self-consistently. The self-consistent method of solution for the equations involving the dressed fermion propagator, is the usual, such as that one in the Hamiltonian formalism for the decoupled slave-boson representation (Grilli and Kotliar 1990, 1170; Kotliar and Liu 1988, 5142 and Tandon, Wang and Kotliar, 1999, 2046) [12, 13, 14].

Having shown how our model is useful to describe the normal state i.e, the state in which the Cooper-pair amplitude < c_k↑ , c_-k↓ > is zero because of the number conservation.

The key feature of the frequently used Bardeen-Cooper-Schriefer (BCS) theory is the Cooper-pair condensation. The simplest model, which permits the description of the superconducting state, is given by the BCS reduced Hamiltonian formalism. The BCS integral equation is introduced by means of the Gor'kov's method. Next, the superconducting state is incorporated into the formalism by using the Nambu matrix notation (Nambu 1960, 648 and Allen and Mitrovíc 1982, 1) [15, 16].

The purpose of the present paper is to make possible the description of the superconducting state in the framework of our Lagrangian formalism when the pair of states (k↑, -k↓) is coherently occupied. This is done by introducing the Nambu matrix notation in the new non-perturbative large-N expansion for the generalized Hubbard model proposed in Ref. [7].

The aim is to give the formulas for the renormalized physical quantities, such as self-energies and propagators to leading order in 1/N for the superconducting state with Cooper-pair condensation.

The paper is organized as follows. In section 2, the main results of sections 2 and 3 of Ref. [7] are collected, and the Nambu notation is introduced. Next, by using the Nambu matrix notation the Feynman diagrammatics is analyzed up to one loop. In section 3, by using the resulting expression, the 1/N correction to the total fermion self-energy for both the normal and the superconducting states are evaluated. The conclusions are given in section 4.

 

2. Nambu notation: Definitions and Diagrammatics

For the slave-boson representation for the generalized Hubbard model describing N-fold-degenerate correlated bands, the non-perturbative large-N expansion technique is used routinely, Refs. [12,13,14]. Also the large-N expansion was used in functional theories written in terms of the X-operators (Zeyher and Kulíc 1996, 2850 and Zeyher and Greco 1998, 473) [17, 18], and was shown that in order 1/N the method gives different results for superconductivity.

By using our Lagrangian model written in the framework of the path-integral formalism a new non-perturbative large N-expansion was proposed, Ref. [7]. The generalized Hubbard model is described by means of the introduction of a set of fermion field ƒ_ip , in such a way that their proportionality with the fermion-like Hubbard X_i^0p operators is maintained for all order in the large-N expansion. Looking at the Lagrangian equation (2.17) of Ref. [7], we see that it is sufficient to retain terms up to order δR_i² to take into account all the terms of order 1/N. Thus the Lagrangian is written:

Haga clic para agrandar

In Ref. [7] is proved that our Lagrangian formalism for the t-J model is a second-class constrained system. The physical quantities such as propagators and vertices were renormalized by means of the introduction of proper ghost fields. Therefore in the present paper we assume that all the physical quantities we must handle were previously renormalized.

Thus we can easily construct the diagrammatics from the Lagrangian (1) in the U-infinite limit (J_ij = 0).

Taking into account the superconducting state, the renormalized fermion propagator Ĝ_(D) is a 2x2 matrix schematically written:

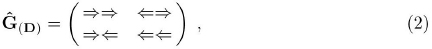
where the diagonal elements with the two arrows pointing in the same direction are the normal fermionic propagators, while the non-diagonal elements with the two arrows pointing in the opposite direction are the anomalous fermionic propagators.

Introduce the Nambu matrix notation is a simple way of describing the fermionic sector when the complete fermionic propagator is of the form (2), Ref. [15]. In this notation the two-component fermionic field operator ψ_im(x,τ) is given by:

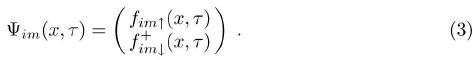
The Lagrangian (1) in terms of the field operator ψ_im(x,τ)is written:

Haga clic para agrandar

where we have named μ = μ' – λ₀.

We can see from the equation (4) that the bosonic sector (third term) described by the two field components (δR_i, δλ_i) remains unchanged, and the fermionic sector (first, second and fourth terms) was written by using the 2x2 Pauli matrices I and τ₃. Therefore, to describe non-diagonal quantities that appear in the fermionic propagator when considering the superconducting state, the four Pauli matrices are introduced.

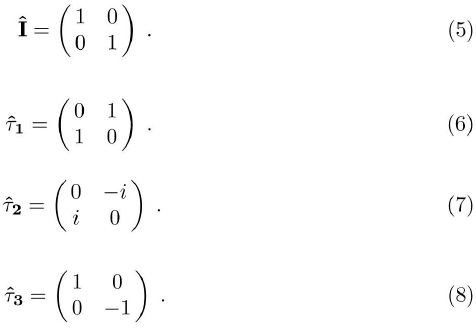
The two-component fermionic field operator (3) in the momentum space reads:

and

Using the previous notation, we study the diagrammatics for both normal and superconducting states with the objetive to find the equation for the total fermion self-energy and hence to write the renormalized fermion propagators to leading order of large-N expansion.

The Feynman rules and the diagrammatics can be obtained, and compute the 1/N corrections to the propagators, we will study the structure of the model to one loop.

The equations are written in the momentum space, and so once the Fourier transformation was performed, the bilinear parts of the Lagrangian (4) give rise to the field propagators and the remaining pieces are represented by vertices.

The boson sector remains unchanged, and the free boson propagator associated with the two component boson field δX^α = (δ R, δ λ) , is of order 1/N and it is written:

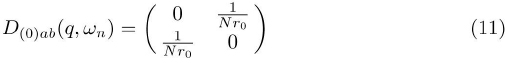
where the quantities q and ω_n are respectively the momentum and the Matsubara frequency of the bosonic field.

We wear the free propagator (11) using the Dyson equation D_ab ^-1 = D_(o)ab ^-1 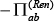[7], equations (4.4) and (4.5), the boson self-energy and the dressed components D_RR(q, ω_n), D_λR (q, ω_n) and D_λλ (q, ω_n) of the matricial boson propagator were found.

The renormalized boson propagator we found is the suitable one that permits us to evaluate for instance the 1/N correction to the fermion self-energy.

It is important to note that when only the normal state is considered, our diagrammatics was checked by computing numerically the charge-charge and spin-spin correlation functions on the square lattice for nearest-neighbor hopping t, Ref. [11]. The results are in agreement with previous ones arising from the slave-boson model as well as from the functional X-operators canonical approach (Gehlhoff and Zeyher 1965, 4635 and Wang 1992, 155) [19, 20].

The bilinear fermionic part of the Lagrangian (4) in the momentum space reads:

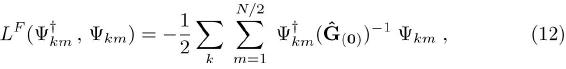
where the 2x2 matrix Ĝ₍₀₎ ^-1 is given by:

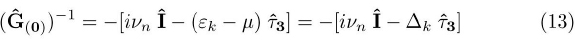
and whose determinant is written:

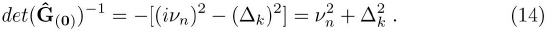
where was defined ε_k = –r₀t Σ_I exp(–il · k); and I is the lattice vector.

The quantities k and v_n are respectively the momentum and the Matsubara frequency of the fermionic field.

Therefore the free fermion propagator Ĝ₍₀₎ is:

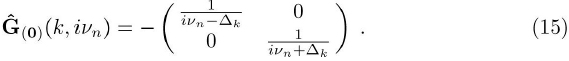
where we call Δ_k = (ε_k - μ), having the property Δ_k = -Δ_k. From this property it can be seen that:

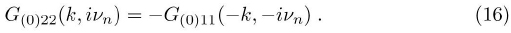
For noninteracting band electrons, the off-diagonal elements in (2) vanish, and the element G₍₀₎₁₁ has the usual scalar form - iv_n -Δ_k ^-1 Ref. [7].

The matrix equation (15) in terms of the Pauli matrices can be written:

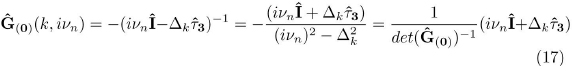
Examining the equation (4) it can be seen that the three-leg (one boson-two fermions) and four-leg (two bosons-two fermions) vertices, are respectively originated by the following pieces of that Lagrangian:

Haga clic para agrandar

Haga clic para agrandar

Therefore the vertices can be written:

 

 

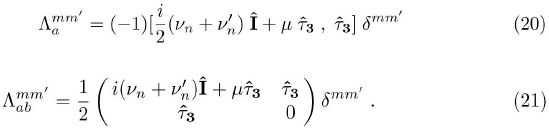
Thus, the Feynman diagrammatics the expression for the 1/N correction to the fermion self-energy for the normal and the superconducting states can be written.

 

3. The fermion self-energy for the normal and the superconducting states, 1/N correction

In the introduction it was mentioned that the simplest model suitable to describe the superconducting state is given by the BCS reduced Hamiltonian formalism. In the normal state such formalism reduces to Migdal's theory whose essence is to use only the lowest order Feynman diagram provided by the reduced Hamiltonian (Bardeen, Cooper and Schrieffer 1957, 1175) [21].

In this model the total fermion self-energy Σ for the normal state is given by the sum of contributions corresponding to the following two one-loop diagrams:

In the Nambu matrix notation the matrices 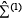and 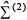respectively are written:

Haga clic para agrandar

Haga clic para agrandar

From the above equations the 1/N correction to the fermion self-energy can be computed, Ref. [13].

Alternatively the matrices 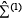and 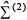can be written:

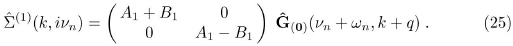
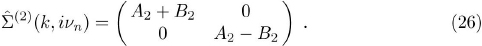
where:

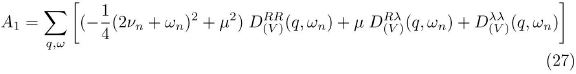
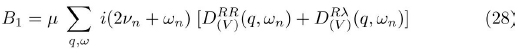
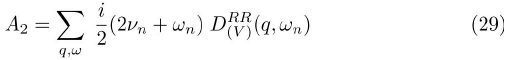
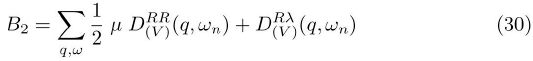
Therefore, for the normal state the total fermion self-energy is a diagonal matrix which in terms of the Pauli matrices can be explicitly written as follows:

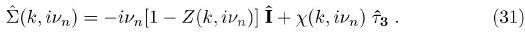
The fermionic dressed propagator is defined by means of the Dyson equation:

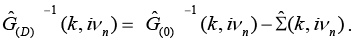
The above equations are suitable to describe the leading 1/N corrections for the normal state in the generalized Hubbard model describing N-fold-degenerate correlated bands in the infinite-U limit. They were obtained by means of a new non-perturbative large-N expansion in the framework of our Lagrangian model.

Now the superconducting state must be incorporated. By looking at the expression of the fermionic self-energy (equation (32)) we assume that the most general form to write the total self-energy in terms of the Pauli matrices is:

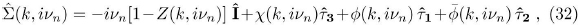
where Z, χ , Φ and 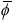are four independent arbitrary functions.

When the superconducting state is taken into account the "anomalous" dressed fermionic propagator also is determined by the Dyson equation, consequently:

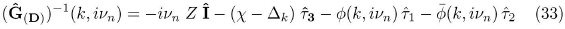
This matrix can be inverted, and it results:

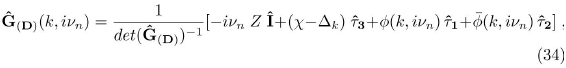
where:

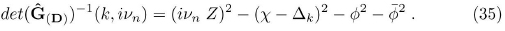
It is clear that the Dyson perturbation series for the matrix Ĝ_(D) turns out to be identical to that for G_(D). The only difference is that Ĝ_(D)is a matrix and that factors of the Pauli matrices are attached in the interaction matrix elements.

Since in the normal state the fermionic propagator Ĝ_(D) is diagonal, it is clear that the both arbitrary functions Φ and 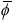must vanish. The arbitrary functions Z and X ªare univocally determined by the normal state, and in order to verify the property (16) both quantities must be even functions of iv_n. The "normal" solution Φ = 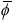= 0 always exists. So, the functions Z and X in the normal state remain defined by the following equations:

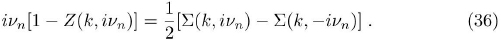
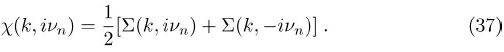
where it was assumed that everything is even in the momentum k.

Furthermore we assume that the property (16) is maintained in the superconducting state, and so is necessary that Φ² + 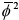must be also an even function in iv_n. Moreover, it is possible to see that Φ and 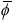satisfy identical nonlinear equations. Consequently, except a proportionality factor (phase factor) both functions must be equals. When a solution Φ, 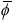with one or both functions different from zero exists, it is possible to show that it describes the state with Cooper-pair condensation (the superconducting state) (Bardeen and Stephen 1964, 1485) [22].

The simplest solution is to take Φ ≠ 0 and 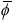= 0 corresponding to fix the phase factor. This is possible because the physical observables cannot depend of this phase. This choice is equivalent to write the self-energy in terms of the real Pauli matrices.

As it occurs in the normal-state case, the equation for the total fermionic self-energy must be solved self-consistently by using the equation (34). As it is usual the explicit computation is carried out by introducing the spectral representation of the boson propagator.

 

Conclusions

The BCS theory is the model capable to describe the superconducting state. The Cooper-pair amplitude < c_k↑ , c_-k↓ >which is zero in the normal-state due to the number conservation becomes finite bellow Tc. An important feature of BCS theory is the Cooper-pair condensation, in this approach the pair of states (k↑, -k↓) is occupied coherently. The simplest model which permits such behavior is the BCS reduced Hamiltonian model.

A Lagrangian family that can be mapped in the slave-boson representation was previously studied, Ref. [7]. In the case of the normal-state the nonperturbative formalism for the generalized Hubbard model by using a new large-N expansion in the infinite-U limit was given. The standard Feynman diagrammatics was constructed, in order to compute the 1/N correction to the boson propagator. The structure of the model was examined in detail up to one loop. The renormalized boson propagator we found is the suitable one that permits us to evaluate the 1/N correction to the fermion self-energy. In the normal-state case, the diagrammatics was checked by computing numerically the charge-charge and spin-spin correlation functions on the square lattice for nearest-neighbor hopping t. The results obtained in Ref. [11] are in agreement with previous one arising from the slave-boson model as well as from the functional X-operators canonical approach.

In the present paper, by using the Nambu matrix notation we have rewritten the Lagrangian for the t-J model and the Feynman diagrammatics was constructed but now taking into account the superconducting state. In this situation propagators and vertices were again evaluated. The renormalized physical quantities to leading order in 1/N were computed, and the equation for the total fermion self-energy which must be solved self-consistently was found. So, we have given the theoretical framework suitable to describe the superconducting state in the Lagrangian formalism for the generalized Hubbard model.

 

References

[1] G. Kotliar and J. Liu, Phys. Review B 38 (1988) 5142;         [ Links ] M. Grilli and G. Kotliar, Physical Review Letters 64 (1990) 1170.         [ Links ]

[2] A. Tandon, Z. Wang and G. Kotliar, Physical Review Letters 83 (1999) 2046.         [ Links ]

[3] A. Izyumov, Physics - Uspekhi 40 (1997) 445.         [ Links ]

[4] P. Coleman, J. Hopkinson and C. Pépin, Phys. Review B 63 (2001) 140.         [ Links ]

[5] A. Foussats, A. Greco and O. S. Zandron, Annals of Physics (NY) 275 (1999), 238.         [ Links ]

[6] A. Foussats, A. Greco, C. Repetto, O. P. Zandron and O. S. Zandron, Journal of Physics A 33 (2000) 5849.         [ Links ]

[7] A. Foussats, C. Repetto, O. P. Zandron and O. S. Zandron, International Journal of Theoretical Physics 41 (2002) 1053, and bibliography counted in therein.         [ Links ]

[8] C. Abecasis and O. Zandron, "Diagrammatics and Feynman rules in the Lagrangian theory based on the spl(2,1) graded algebra", International Journal of Modern Physics B 21 (2007) 1861.         [ Links ]

[9] J. J. Liang, J. Q. Liang and W. M. Liu, Phys Rev. A 68 (2003) 436.         [ Links ]

[10] Z. W. Xie and W. M. Liu, Phys. Rev. A 70 (2004) 456.         [ Links ]

[11] A. Foussats and A. Greco, Phys. Rev. B 65 (2002) 195107.         [ Links ]

[12] M. Grilli and G. Kotliar, G, Phys. Rev. Lett 64 (1990) 1170.         [ Links ]

[13] G. Kotliar and J. Liu, Physical Review: Condensed Matter B 38 (1988) 5142.         [ Links ]

[14] A. Tandon, Z. Wang and G. Kotliar, Phys. Rev. Lett 83 (1999) 2046.         [ Links ]

[15] Y. Nambu, Phys. Rev. 117 (1960) 648.         [ Links ]

[16] P.B. Allen and B. Mitrovíc, Theory of Superconducting Tc, Solid State Physics 37 (1982) 1.         [ Links ]

[17] R. Zeyher and M. Kulíc, Phys Rev. B 53 (1996) 2850.         [ Links ]

[18] R. Zeyher and A. Greco, Eur. Phys. J.B. 6 (1998) 473.         [ Links ]

[19] L. Gehlhoff and R. Zeyher, Physical Review B 52 (1965) 4635.         [ Links ]

[20] Z. Wang, International Journal of Modern Physics B 6 (1992) 155.         [ Links ]

[21] J. Bardeen, L.N. Cooper and J.R. Schrieffer, Phys. Rev. 108 1175 (1957).         [ Links ]

[22] J. Bardeen and M. Stephen, Phys. Rev. A 136 1485 (1964).         [ Links ]