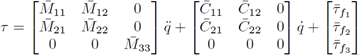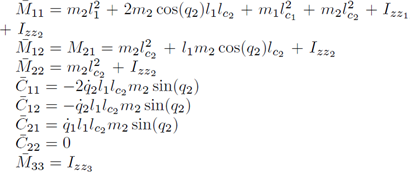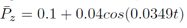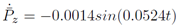I. Introducción
Actualmente la demanda de sistemas mecatrónicos en procesos industriales, robótica de servicios, entre otros, está en constante crecimiento requiriendo de productos de mayor calidad a menor precio y a su vez con un incremento en su productividad. Con ésta idea, se han realizado esfuerzos por parte de investigadores para mejorar el desempeño de los robots, al desarrollar estrategias de control avanzadas, como por ejemplo, control adaptable y predictivo [1], control de fuerza [2], control por modos deslizantes [1], e incluso con estrategias de control inteligente como por ejemplo control por medio de una redes neuronales artificiales [3], [4] y en lógica difusa [5], [6]. Sin embargo la mayoría de estos esfuerzos se han quedado en prototipos de investigación debido a que los robots comerciales presentan limitaciones en su controlador haciendo más tardía su implementación industrial. Es así, que la arquitectura de control de sistemas mecatrónicos se puede clasificar en tres tipos [7], [8]: i) Arquitectura de propiedad (cerrada) en donde la estructura de control así como el protocolo propio de comunicación y detalles técnicos se encuentran ocultas para el usuario y es una tarea difícil o imposible integrar hardware (sensores) y hacer modificaciones en el sistema de control. ii) Arquitectura híbrida en donde la estrategia de control es cerrada pero algunos aspectos permanecen abiertos como la posibilidad de agregar nuevos dispositivos como sensores. iii) Arquitectura de control abierta en donde todos los aspectos de hardware y software pueden ser modificados sin dificultad por el usuario, tales como, sensores, interfaz gráfica de usuario, estrategias de control, etc. incrementando la capacidad y actualización del producto.
A pesar de que la tendencia actual es el diseñar sistemas de arquitectura abierta con el fin de tener un sistema flexible, reconfigurable, versátil, la mayoría de los controladores de robots comerciales (aunque se diga que es de arquitectura abierta), son del tipo cerrado o híbrido. Es así, que se han estado realizando esfuerzos para dotar de arquitectura de control abierta en robots o sistemas industriales. El sistema de arquitectura abierta se puede desarrollar por medio de sistemas embebidos de propósitos específicos o por medio de una computadora, siendo este último la tendencia actual ya que permite mucha mayor flexibilidad y versatilidad en la implementación de dicha arquitectura. A la arquitectura abierta que se desarrolla en una computadora se le nombra arquitectura abierta por medio de una computadora personal. En [9] se adapta un sistema de control de arquitectura abierta en un robot industrial PUMA 560 y se prueban diversas estrategias de control tales como control adaptivo a través de una regresor, controlador PD, entre otras. Se muestra que al implementar sistemas de control avanzados se puede mejorar en gran medida el desempeño de un robot industrial. En [10] se propone un sistema de control distribuido multi-agente de arquitectura abierta para una máquina de control numérico. El resultado obtenido muestra que es fácil implementar estrategias de control y características del monitoreo con el sistema propuesto.
Desde 1980 hasta el día de hoy, la filosofía de diseño de controladores de arquitectura abierta ha tomado gran atención, primeramente en el área de manufactura avanzada en el sistema de control de máquinas de control numérico (MCC). El primer controlador de arquitectura abierta fue el sistema MOSAIC desarrollado por la universidad de Nueva York en 1998 [11]. En 1992 se introduce uno de los sistemas de arquitectura abierta más importantes dentro del proyecto europeo OSACA [12]. Posteriormente en 1994 en Japón, se establece el proyecto OSEC bajo el consorcio de IROFA [13] y posteriormente varios investigadores de Estados Unidos adquieren un progreso sobresaliente en el ámbito de automatización de máquinas y control. Actualmente, en [14] se ha desarrollado una metodología para el diseño de sistemas de arquitectura abierta, que resulta en una arquitectura de hardware y software que es portable e integrada al sistema mecatrónico, de tal manera que se puedan implementar estrategias de control avanzada. En [15] se describe la arquitectura PC-ORC el cual es un sistema de control de arquitectura abierta en una computadora personal que se estableció de manera similar al modelo de referencia OSACA y se ha utilizado para realizar tareas básicas en un robot SCARA. La filosofía de arquitectura abierta se ha aplicado también a robots humanoides [16].
En este artículo se describe el diseño de un sistema de control de arquitectura abierta por medio de una computadora personal el cual proporciona a un sistema mecatrónico la flexibilidad, reconfigurabilidad y versatilidad para realizar una amplia variedad de tareas (dependiendo de la aplicación) considerando bajo costo, para así utilizarlo en las escuelas y/o investigación. Debido a que Matlab-Simulink es el desarrollador líder mundial de programas para la ingeniería, ciencia, gobierno y educación, así como por su fácil manejo, se propone como lenguaje de programación base para el desarrollo e implementación de las tareas a desarrollar por el sistema mecatrónico. Además se presentan los resultados experimentales en un sistema robótico de tres grados de libertad bajo el esquema de control par calculado, ilustrando el desempeño y beneficios de la arquitectura de control propuesta.
II. Arquitectura de control abierta
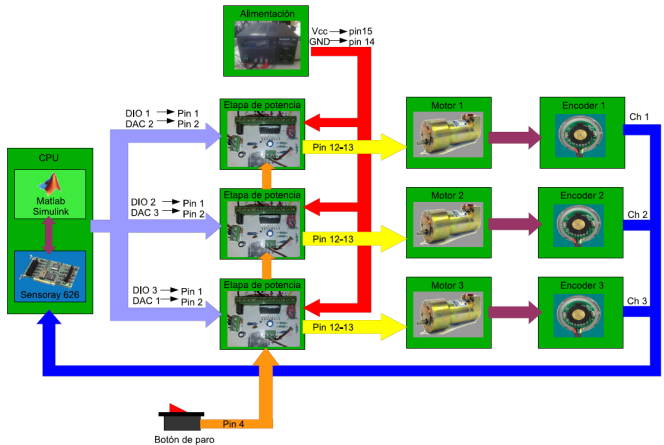
Siguiendo la filosofía descrita en [14] se establece la arquitectura de control abierta por medio de una computadora personal mostrada en la Figura 1. Se observan varios niveles de jerarquía, entre los que se encuentran: i) El nivel de aplicación en donde se implementa la interfaz gráfica de usuario. ii) Nivel de control en donde se programa la estrategia de control. iii) Nivel de interfaz en donde se interpretan las variables físicas del sistema mecatrónico en variables que pueda interpretar el nivel de control y a su vez proporcionar la acción de control. iv) Nivel de dispositivos en donde se encuentran los sensores, actuadores así como acondicionamiento de señal.
Para el caso en particular de la arquitectura de control abierta por medio de una PC, en el nivel más bajo (nivel de dispositivos) están los sensores (decodificadores ópticos, sensor de fuerza, cámara, etc.), la etapa de potencia y los motores de corriente directa (CD) del sistema mecatrónico. La etapa de potencia consiste en el circuito integrado (C.I.) "LMD18245" que es un amplificador de potencia de puente completo de bajo costo y que presenta el modo de operación de par (corriente) que es muy importante para emplear el modelo estático del motor y así facilitar la simulación del control de sistemas mecatrónicos. Además el C.I. cuenta con una salida analógica que es proporcional a la corriente que circula por el motor y la cual servirá como sensor de corriente del motor. El nivel de interfaz consiste en los periféricos de entrada y salida que contiene una computadora normalmente (puerto serial, usb, video, audio, etc.) y en una tarjeta de entradas y salidas analógicas y digitales de la empresa Sensoray modelo 626 que se conecta a una PC por medio del puerto PCI (Peripheral Component Interconnect en inglés). El nivel de control será el programa que se instale en la PC y que coordine la entrada y salida de señales a través de la tarjeta Sensoray 626 por medio de una librería de enlace dinámico proporcionada por el fabricante. Para nuestro caso, se utilizó una PC Pentium IV a 3.2GHz con 4GB RAM en Windows y se escogió el programa de Matlab-Simulink en el nivel de control debido a que es un lenguaje gráfico, fácil de usar y que la mayoría de los estudiantes de licenciatura y posgrado están usando actualmente. Además, este programa puede implementarse en tiempo real con la librería "Real time workshop" con un tiempo máximo de muestreo de 1ms. Así, en el nivel más alto (nivel de aplicación) se podrán crear interfaces gráficas para el usuario utilizando GUIDE (Graphical User Interface Development Environment) de Matlab.
III. Descripción del sistema mecatrónico
El sistema mecatrónico consiste de un robot SCARA o robot RRR de tres grados de libertad mostrándose en la Figura 2. Tres servomotores Pittman son requeridos, dos de ellos de la serie GM9234S033 con una razón de reducción de 218.14 : 1 para actuar los eslabones 1, 2 y uno de la serie GM9236S015 con una razón de reducción de 5.9 : 1 para actuar el eslabón 3. Los tres cuentan con decodificadores ópticos de 500 pulsos por vuelta.
A. Modelo Cinemático
Considere el diagrama esquemático del robot SCARA mostrado en la Figura 3 donde Oi ∀i = 0;...; 4 es el origen del sistema de coordenadas del sistema inercial, del i-ésimo eslabón y del efector final, respectivamente. La longitud, longitud del centro de masa, la masa y el momento de inercia expresada en el centro de masa del i-ésimo eslabón se expresan como li ∈ R , lci ∈ R, mi ∈ R, Izzi ∈ R3x3 ∀ i = 1; 2; 3; respectivamente.
Definiendo las posiciones y velocidades deseadas en el espacio articular como
Por el método geométrico [2] se calcula la cinemática inversa del robot SCARA presentado por las ecuaciones (4)-(6), donde
B. Espacio de trabajo
El espacio de trabajo real del robot SCARA se muestra en la Figura 4. Para el caso particular se utilizó el espacio de trabajo representado con un prisma rectangular de 0.236 m, 0.193 m, 0.1 m con un desplazamiento lineal sobre el eje O0z de 0.05 m.
C. Modelo dinámico
Considerando que el momento de inercia del eslabón 3 con respecto al eje z3 es pequeño y que su movimiento es a través del plano y-z o x-y, comparada con los momentos de inercia de los eslabones 1, 2 con respecto a los ejes zi ∀i = 1; 2, respectivamente y a su plano de movimiento x-y, se propone desacoplar la dinámica del robot SCARA en un robot del tipo RR y otro del tipo R.
Siguiendo el formalismo de Euler-Lagrange [2] se puede obtener el modelo dinámico del robot SCARA desacoplado mostrado en (7).
donde:
D. Sistema de control
Se propone un controlador par calculado [2] para seguir
una trayectoria, cuyo esquema es el mostrado en (8) donde
Se escoge que el robot realice en el efector final un círculo en 120 s de radio 0.07 m en el plano x-y del espacio Cartesiano con centro en las coordenadas (0m; 0.17m) y en el eje z que realice un movimiento oscilante alrededor de 0.10m con una amplitud de 0.04m y un periodo de 180s, por lo que se propone la trayectoria descrita en (9)-(14).
IV. Resultados en simulación y experimental
Para realizar los resultados en simulación se requiere de los parámetros cinemáticos (Param. Cin.) y los parámetros dinámicos (Param. Din.) del robot SCARA. Dichos parámetros se obtienen con la ayuda del programa de diseño paramétrico SolidWorks y se muestran en la Tabla I. En esa misma tabla se muestran las ganancias para el sistema de control (Gan. Ctrl.). Las ganancias fueron escogidas a prueba y error.
Tabla I Parámetros del robot SCARA, ganancias del controlador y coeficientes de fricción de cada unión.

Se utilizó el programa Matlab-Simulink para realizar la simulación numérica con el método de
Runge-Kutta de 4to orden con un tiempo de integración
Δts = 5E - 3s, un
tiempo final tf
= 120s y un vector de condición inicial q(t0)
= [0; 0; 0]T ubicando al efector final en (0:3062 m, 0
m, 0:0567 m). Para realizar los resultados experimentales se
consideró la misma condición inicial en el manipulador, se propuso un tiempo de
muestreo de Δte
= 5E - 3s y se requirió del modelo
estático del motor (
El sistema experimental con la arquitectura de control abierta por medio de una PC se muestra en la Figura 5 y en la Figura 6 se muestra el diagrama esquemático.
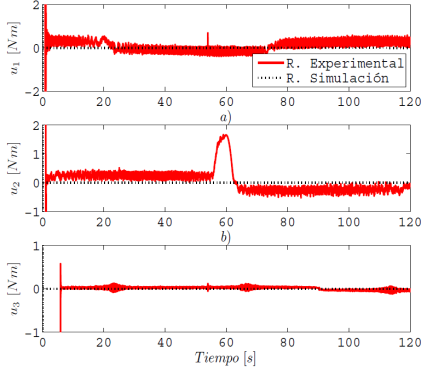
La trayectoria deseada en el espacio articular se calcula en línea. Los resultados en simulación y experimental en el seguimiento de la trayectoria del efector final se muestra en la Figura 7 para el plano x-y y en la Figura 8 para el eje z. Se observa en la Figura 9 que pasando el transitorio inicial, el máximo error en el efector final de la distancia del centro del círculo al radio del círculo de la trayectoria deseada es de 1E-8 m en la simulación y de 9E-4 m en los experimentos; y el error máximo de la trayectoria en z es de 2E-9 m en simulación y de 7E- 6 m en los experimentos, los cuales son aceptables para efectos didácticos, de laboratorio y de investigación. Cabe mencionar que el error producido en el tiempo 60s de la Figura 9a se debe a una falla mecánica la cual provoca que la fricción en el eje 2 sea mayor y su vez se incremente la señal de control, como se observa en la Figura 10b. Dicho error puede disminuirse al aplicarle otra estrategia de control que compense las no linealidades producidas por la fricción. Así, en la Figura 10 se muestra la señal de control requerida para seguir la trayectoria.

Figura 7 Resultados en simulación y experimental del seguimiento de la trayectoria en

Figura 8 Resultados en simulación y experimental del seguimiento de la trayectoria en

Figura 9 Divergencia entre la distancia del centro de círculo y la trayectoria real - simulada con el radio del círculo (o.07m). Error en el seguimiento de la trayectoria
Es importante resaltar la correspondencia entre los resultados de simulación y experimentales, lo cual indica la importancia de modelar el sistema mecatrónico y probar estrategias de control primeramente en simulación y una vez que el desempeño del controlador sea el adecuado implementarlo físicamente, esto con el propósito de evitar daños en el sistema real.
Actualmente el sistema mecatrónico y la arquitectura de control abierta por medio de una PC se está utilizando en el curso de robótica de manipuladores y sistemas de control no lineal que se ofrecen en la Maestría de Tecnología de Cómputo en el Centro de Innovación y Desarrollo Tecnológico en Cómputo del Instituto Politécnico Nacional (CIDETEC-IPN), dando como resultado que los alumnos comprendan y apliquen de una mejor manera los conceptos proporcionados en clases.
A. Análisis comparativo de la arquitectura de control abierta por medio de una PC
Con el propósito de mostrar las bondades de la propuesta de arquitectura de control abierta por medio de una PC, se realiza una comparación con otras dos arquitecturas, una reportada en la literatura [18] y otra producida por la empresa Quanser. Para realizar una comparación justa con arquitecturas similares, se definió como criterio, que debería ser a través de una PC y con compatibilidad con Matlab-Simulink. La comparación se dirige principalmente en el costo.
En [18] se utilizan los productos de dSpace para realizar el enlace entre la computadora y el hardware (adquisición y envío de señales) por lo que además de necesitar un programa de la aplicación en Simulink, se requiere pasar dicho programa en la interfaz de usuario propia de la empresa dSpace (dSPACE CONTROLDESK). Las ventajas de utilizar los productos dSpace es su precisión y su alta tasa de muestreo. Sin embargo para algunas aplicaciones en sistemas robóticos, ésto podría resultar excesivo. Por otro lado, las tarjetas de adquisición de datos de la empresa dSpace normalmente tienen un costo elevado. En el trabajo presentado en [18] se utilizaron seis tarjetas de adquisición de datos (DS1004, DS1003, DS2001, DS2102, DS3002 y DS4001) por lo que el costo de dicha arquitectura es muy elevado a pesar de que no se está considerando el costo del robot.
El otro punto a comparar es con la empresa Quanser, que ha promovido sistemas mecatrónicos didácticos con diseños de arquitectura abierta compatibles con Matlab-Simulink. Ofrecen varios sistemas mecatrónicos cuyo precio es alto y en donde se incluye el robot. Los prototipos que ofrecen son muy básicos en su manufactura y el sistema de sensado. Sin embargo, ofrecen mucha documentación y prácticas de laboratorio muy didácticas, que las hacen muy atractivas en la academia.
La arquitectura de control por medio de una PC que se propone en este trabajo es muy económico (alrededor de $950.00 dólares estadounidenses sin incluir el robot) que puede ser implementado fácilmente en cualquier laboratorio para validar la teoría de una forma rápida y con una precisión aceptable. Además, debido a que trabaja con Matlab-Simulink, se pueden realizar mejoras en el entorno gráfico. Finalmente, en la Tabla II se muestra una tabla comparativa de la propuesta de arquitectura abierta presente en este trabajo con respecto a las otras dos arquitecturas mencionadas previamente. Se muestra con el símbolo † la cantidad de veces que se eleva el costo con respecto a la propuesta en este artículo. Se observa que la propuesta de arquitectura abierta mostrada en este trabajo realmente presenta un costo relativamente bajo.
V. Conclusiones
En este artículo se ha presentado una arquitectura genérica para el control de sistemas mecatrónicos por medio de una PC. Esta arquitectura es evaluada en un robot SCARA en donde se le implementó exitosamente una estrategia de control para el seguimiento de trayectoria. La arquitectura de control abierta hace posible que la etapa experimental sea más rápida, eficiente y con un costo muy bajo comparado con otras arquitecturas similares. Por otra parte, en el ámbito académico y de investigación es muy útil esta arquitectura, debido a que se puede validar la teoría con la práctica, al verificar que los resultados en simulación numérica coinciden con un mínimo de error con los experimentales, siempre y cuando se identifiquen adecuadamente los parámetros del modelo del sistema mecatrónico a controlar. Además es muy importante realizar primeramente las simulaciones numéricas del sistema a controlar antes de llevar a cabo los resultados experimentales para evitar daños en el sistema real debido a una mala sintonización del controlador.











 nueva página del texto (beta)
nueva página del texto (beta)