Introducción
El mercado cambiario constituye uno de los mercados financieros más importantes. Esto se debe al volumen de comercio diario, así como por su incidencia en el comportamiento de otros mercados, sean de activos financieros o de bienes y servicios (Sosvilla- Rivero, 2011). Por ejemplo, Samson (2013) muestra que el tipo de cambio tiene un fuerte impacto en el precio de los activos y el valor de las firmas, y Aron, Farrell, Muellbauer y Sinclair (2014) muestran que el tipo de cambio tiene una estrecha relación con los niveles inflacionarios y la respuesta del mercado a la política monetaria.
El objetivo de este artículo consiste en proveer de evidencia para la elección correcta de un modelo para el mercado cambiario. Esto resulta de particular interés para aquellos inversionistas interesados en la valoración de derivados financieros, especialmente las opciones sobre el tipo de cambio. De igual forma, la correcta estimación del proceso que sigue el tipo de cambio es útil para las instituciones financieras que deseen anticipar el capital económico requerido para hacer frente a pérdidas no anticipadas y, en particular, para seleccionar un método adecuado para la determinación de su capital regulatorio bajo la exposición al riesgo de mercado a través del Valor en Riesgo (VaR).
El procedimiento tradicional para modelar el comportamiento de los activos financieros, incluidas las divisas, consiste en suponer que sus precios siguen algún proceso basado en la distribución normal (a través de la aplicación de un proceso de Wiener). En su versión más simple, puede suponerse que el precio de los activos sigue un movimiento browniano geométrico (MBG). Esto implica que el precio de los activos sigue una distribución lognormal y, por lo tanto, su tasa de rendimiento sigue una distribución normal, la cual estaría garantizada por el teorema del límite central.2 Sin embargo, el supuesto de normalidad ha sido rechazado en varios análisis. Por ejemplo, Mandelbrot (1963) muestra que la distribución del rendimiento en el precio de algunos activos financieros tiene colas más pesadas en relación con una distribución normal y Fama (1965) muestra que, además de tener colas más pesadas, la distribución de los rendimientos puede tener un pico más pronunciado en el centro.
Recientemente, varios autores han utilizado una combinación de procesos basados en la distribución normal con una distribución de Poisson, lo cual permite capturar la persistencia en la varianza condicional de los rendimientos (Maheu & McCurdy, 2008). Otros modelos que también permiten mejorar el ajuste de los rendimientos de los precios de los activos financieros en relación con la distribución normal son los de la familia de distribuciones hiperbólicas (Bibby & Sørensen, 1996; Eberlein & Keller, 1995). Estos modelos se han utilizado recientemente para modelar, por ejemplo, el tipo de cambio del dólar estadounidense frente al REAL brasileño (Fajardo Barbachan, Rocha de Farias & Haas Ornelas, 2005), el tipo de cambio Krone noruego frente al euro (Aas & Haff, 2006) y el euro frente a la corona sueca, de la libra esterlina frente a la corona sueca y el dólar de Estados Unidos frente a la corona sueca (Tichy, 2012).
En este artículo modelamos el comportamiento del tipo cambio del peso mexicano (MXN) respecto del dólar de Estados Unidos (USD). Mostramos primero que el MBG no ajusta bien a la tasa de depreciación del tipo de cambio. Esto puede constatarse mediante la simple exploración estadística de los datos, así como mediante diferentes pruebas de bondad de ajuste. Intuitivamente, el supuesto de normalidad falla en el mercado cambiario debido a que la información que influye en la formación del tipo de cambio no llega al mercado con una intensidad constante. Cuando el entorno económico es más volátil, aumenta la probabilidad de que los precios presenten grandes saltos sorpresivos. En contraste, si las economías son más estables, los precios tienden a variar muy poco. Para modelar este comportamiento, en este artículo utilizamos un miembro particular de la familia de distribuciones hiperbólicas generalizadas que ha sido introducida por Madan, Carr y Chang (1998) y se conoce como proceso varianza-gamma (PVG). Al igual que el MBG, el PVG también supone que los movimientos en el precio siguen un proceso de Wiener, pero su deriva depende de un proceso estocástico que sigue una distribución gamma.3 Si siguen un PVG, los cambios en el precio son descritos por un número infinito de saltos. La probabilidad con la aparecen estos decrece conforme aumenta el tamaño del salto; es decir, los más pequeños tienen una probabilidad muy alta de aparecer en comparación con los largos. Además, el PVG tiene una distribución leptocúrtica -con una figura picuda y colas más largas en relación con una distribución normal-. A diferencia del MBG, el PVG captura el sesgo y el exceso de curtosis de los cambios en el precio (Finlay, 2009; Tichy, 2012).
Una característica que se observa comúnmente en los trabajos empíricos sobre activos financieros es que los cambios del precio tienen una distribución de probabilidad cada vez más parecida a una normal conforme aumenta la ventana de tiempo para el que fue calculado. Para tener en cuenta este efecto, en este artículo exploramos el ajuste del tipo de cambio MXN/USD a los diferentes procesos considerando rendimientos diarios, semanales y mensuales. Mostramos que, en general, el PVG ajusta mejor a los datos que el MBG para cualquiera de las periodicidades consideradas. Además, mostramos cómo el PVG resulta muy adecuado para calcular el VaR asociado al mercado cambiario.
El resto de este artículo está estructurado como sigue. En la sección “Movimiento browniano geométrico y proceso varianza-gamma” presentamos una breve introducción al MBG y del PVG, así como sus principales características. En la sección “El tipo de cambio en México” describimos el comportamiento del mercado cambiario en México y el tipo de cambio fix. En la sección “Calibración de los log-rendimientos del tipo de cambio” calculamos los rendimientos del mercado cambiario en México para diferentes periodicidades y calibramos los modelos MBG y PVG. En la sección “Comparativa de modelos y bondad de ajuste” comparamos ambos modelos y realizamos algunas pruebas de bondad de ajuste. En la sección “Valor en riesgo y backtesting” calculamos y comparamos el VaR del mercado cambiario utilizando tanto el MBG y el PVG. Finalmente concluimos.
Movimiento browniano geométrico y proceso varianza-gamma
En esta sección presentamos las principales características del MBG y del PVG.4 Ambos procesos tienen dos componentes: a) una tendencia determinista y b) un componente estocástico, el cual captura las desviaciones aleatorias del precio. Dicho componente es conducido por un movimiento de Wiener estándar. La diferencia más importante entre estos procesos es que en el PVG el tiempo natural se ve reemplazado por un tiempo aleatorio, el cual produce movimientos del precio de un tamaño muy distinto a los que pueden generarse en el MBG.
Movimiento browniano geométrico
El MBG es un proceso estocástico en tiempo continuo que resulta de una transformación de un proceso de Wiener estándar. Tiene como particularidad el no permitir que los precios de los activos tomen valores negativos.
Sea {Pt}t≥0, el precio de un activo financiero en tiempo t. Usando la notación diferencial, el MBG se define como:
donde P0 > 0. En la ecuación (1), μ ϵ R es la deriva o tendencia y σ > 0 es un parámetro que mide la volatilidad del precio. Además, Wt es un proceso de Wiener estándar.
Sea yt = ln(Pt). Aplicando el lema de Ito y usando la ecuación (1) obtenemos:
La ecuación (2) implica que yt sigue un proceso browniano aritmético con deriva
Sea Xt = yt - yq. Xt representa el rendimiento continuamente capitalizable sobre un periodo de tamaño ∆t = t - q. A este rendimiento se le conoce como rendimiento logarítmico o log-rendimiento. Cuando P t se refiere al tipo de cambio, X t puede pensarse como la tasa de depreciación. Las propiedades del movimiento browniano estándar nos permiten reescribir la ecuación (3) como:5
Entonces, es fácil deducir que:
lo cual implica que los rendimientos son independientes y tienen una distribución normal. Además, tanto la media como la variabilidad de Xt se incrementan de manera proporcional al tamaño del intervalo de tiempo. Estas propiedades serán analizadas empíricamente en la sección El tipo de cambio en México.
Proceso varianza-gamma
El PVG es un proceso estocástico en tiempo continuo de la familia de las hiperbólicas generalizadas introducido por Madan, Carr & Chang (1998). Al igual que el MBG, el PVG tiene un parámetro de deriva y uno de volatilidad. Sin embargo, se diferencia en que el proceso del rendimiento logarítmico tiene un parámetro de control para el sesgo y otro para la curtosis. Comparado con la distribución normal, el PVG permite modelar rendimientos que presenten una distribución de probabilidad no simétrica y leptocúrtica; es decir, una distribución con figura más alta y colas más anchas.
En el PVG, el tiempo, t, es reemplazado por el proceso gamma, {gt}t≥0. El proceso gamma empieza en cero, y tiene incrementos independientes y estacionarios con distribución gamma dada por (Schoutens, 2003):
Los incrementos del proceso gamma pueden escribirse como {Gt}t≥0 = gt - gq, donde el periodo de tiempo es de ∆t = t - q. con t > q. Los incrementos tienen distribución gamma con media y varianza:
El tiempo aleatorio dado por el proceso gamma suele interpretarse como el tiempo financiero. El objetivo de este es incorporar en el modelo el volumen de las transacciones de mercado, o el flujo de información relevante para la valuación del activo financiero (Finlay, 2009). En este contexto, puede decirse que el tiempo financiero va más aprisa que el tiempo natural cuando el número de transacciones y la cantidad de información es mayor a las cantidades observadas regularmente en un periodo de tiempo natural. Y, al contrario, va más despacio cuando las transacciones son menores o es muy poca la información. El comportamiento del tiempo financiero puede producir variaciones del precio de diversos tamaños. En especial, permite que ocurran variaciones extremas y que estas tiendan a ser mayormente positivas o negativas.6
Por otro lado, puede observarse que el valor esperado del incremento gamma sobre un periodo de tamaño ∆t es justamente ∆t. Esto quiere decir que se espera que el tiempo financiero concuerde con el tiempo natural. En promedio, el tiempo de mercado no transcurre ni más rápido ni más lento que el tiempo natural.
El PVG está dado definido por:
donde, como antes, yt = ln (Pt). En la ecuación (5), μ, θ, σ > 0 son constantes reales y Wt es un movimiento browniano estándar independiente de Gt. Como puede notarse, dyt está ahora descrita por un término de deriva en tiempo natural, μ, y un término de deriva que se desarrolla en tiempo gt, θ. Este último controla el sesgo de la distribución los rendimientos. Por otro lado, σ representa la volatilidad total del proceso, y v es el parámetro de la varianza del incremento gamma, Gt. Este parámetro ajusta la curtosis de la distribución gamma respecto de una distribución normal.
Ya que Xt = -yt - yq. es el rendimiento logarítmico del precio sobre un periodo de tiempo de tamaño ∆t = t - q, se tiene que:
Igual que antes, las propiedades del movimiento browniano (ahora sobre un periodo gt - gq) nos permiten reescribir la ecuación (6) como:
Por lo tanto:
Ahora bien, la función de densidad de Xt puede expresarse como una densidad condicionada a la realización del incremento del proceso gamma. Específicamente:
Expresada de esta forma, tenemos que Xt sigue una distribución normal con media θ(gt - gq) y varianza (gt - gq)σ2. La densidad de cada rendimiento logarítmico se determina por los incrementos del proceso gamma sobre un periodo de tiempo natural.
En contraste, si no condicionamos al incremento gamma, la función de densidad de Xt es (Brigo, Dalessanddro, Neugebauer & Triki, 2009):
para -∞ < x < ∞ y donde B es la función Bessel de tercera clase (Seneta, 2004).
Podemos calcular los momentos de la distribución varianza-gamma para Xt como sigue (Seneta, 2004):
Puede verificarse que si
Finalmente, el proceso del precio sobre un periodo t es:
donde
El valor esperado del precio crece exponencialmente a lo largo del tiempo, y lo hace a una tasa constante μ. Como puede notarse, la media del precio bajo el PVG es idéntica a la media del precio bajo el MBG. Por consiguiente, si los parámetros μ son iguales, el rendimiento esperado del activo sobre t será el mismo para los dos modelos.
El tipo de cambio en México
En este artículo consideramos los datos para el tipo de cambio fix. Nuestra serie comienza el 6 de enero de 1997 y termina el 31 de diciembre de 2014. Esto resulta en un total de 4 527 observaciones. Todos los datos pueden obtenerse de la página de internet del Banco de México (BM).7 La evolución del tipo de cambio se muestra en la Figura 1.

Fuente: Elaboración propia.
Figura 1 Tipo de cambio diario del peso mexicano por dólar estadounidense (6 de enero de 1997 al 31 de diciembre de 2014)
Una característica muy perceptible en el comportamiento del tipo de cambio son los saltos o cambios muy largos en el precio de la divisa estadounidense. En 1998, el valor del peso en dólares sufrió una importante caída debido a que se redujeron los flujos de capital extranjero en México como consecuencia de la inestabilidad financiera de otros países. La reducción de la entrada de capitales tanto a México como a varios países latinoamericanos fue provocada, principalmente, por el colapso financiero y los problemas económicos de Asia, la depreciación de la moneda de Tailandia, Hong Kong y Japón y por la crisis cambiaria de Rusia. Además, el peso se vio afectado por la desconfianza sobre la solidez de las monedas pertenecientes a economías de Latinoamérica, sobre todo del REAL brasileño que tenía un régimen cambiario fijo.
De septiembre de 2008 hasta casi la parte media de 2009 se observaron los saltos más graves del tipo de cambio. Dicha época se caracterizó por un abrupto aumento de la volatilidad en los mercados cambiarios y financieros internacionales tanto de economías desarrollados como de economías emergentes. Así mismo, empeoró el desempeño de las actividades económicas en el nivel mundial, que aumentó la percepción de riesgo de los países. Incluso se generaron expectativas sobre un colapso del sistema financiero internacional. Este comportamiento obedeció a la crisis del mercado financiero de Estados Unidos de finales de 2007. Estas condiciones redujeron los flujos de capital hacia México, lo cuales, a su vez, incrementaron la volatilidad del dólar respecto del peso y afectaron la liquidez del mercado de cambios.
A partir del 2011 hasta el 2012, la volatilidad de los mercados financieros internacionales tuvo un aumento muy significativo y el crecimiento económico de los países disminuyó. En los países con economías emergentes decreció también el flujo de capitales, lo cual provocó mayor volatilidad y depreciación de las monedas de estos países con respecto del dólar. Este hecho se debe, principalmente, a que aumentó la incertidumbre y la aversión riesgo entre los inversionistas por la crisis de deuda soberana y de la economía que enfrentaban los países de la zona euro. Gran parte de las inversiones en economías en desarrollo se reemplazaron por activos que se consideran como refugios de valor, por ejemplo, los bonos del Tesoro de Estados Unidos.
En los últimos meses de 2014, el peso mexicano, al igual que otras divisas de países con economías emergentes, sufrió una caída considerable respecto del dólar. La tendencia de depreciación del peso continuó hasta el año 2015. Estos movimientos del tipo de cambio se deben, fundamentalmente, a las expectativas acerca del aumento en las tasas de interés de la Reserva Federal de Estados Unidos. El aumento en las tasas tiene relación con el crecimiento de la actividad económica y la disminución del desempleo de Estados Unidos. La percepción de conseguir mayores ganancias provoca que los participantes de los mercados financieros conviertan los bonos de deuda que tienen en economías emergentes por inversiones en ese país. El incremento del tipo de cambio del peso por dólar se ve favorecido por la caída del precio del petróleo, que disminuye la entrada de divisas a México.
Calibración de los log-rendimientos del tipo de cambio
En esta sección consideramos el rendimiento logarítmico del tipo de cambio para diferentes periodicidades: rendimiento diario, semanal y mensual. Sea k la distancia de tiempo -los días- que separa las observaciones del tipo de cambio. Entonces:
De esta manera, obtenemos las tres series de rendimiento fijando k = 1 para el caso diario, k = 5 para el caso semanal y k = 20 para el caso mensual. Los precios son equidistantes por k número de días, lo cual hace que los rendimientos no estén traslapados. En la Figura 2 mostramos el comportamiento de las diferentes series de rendimientos.
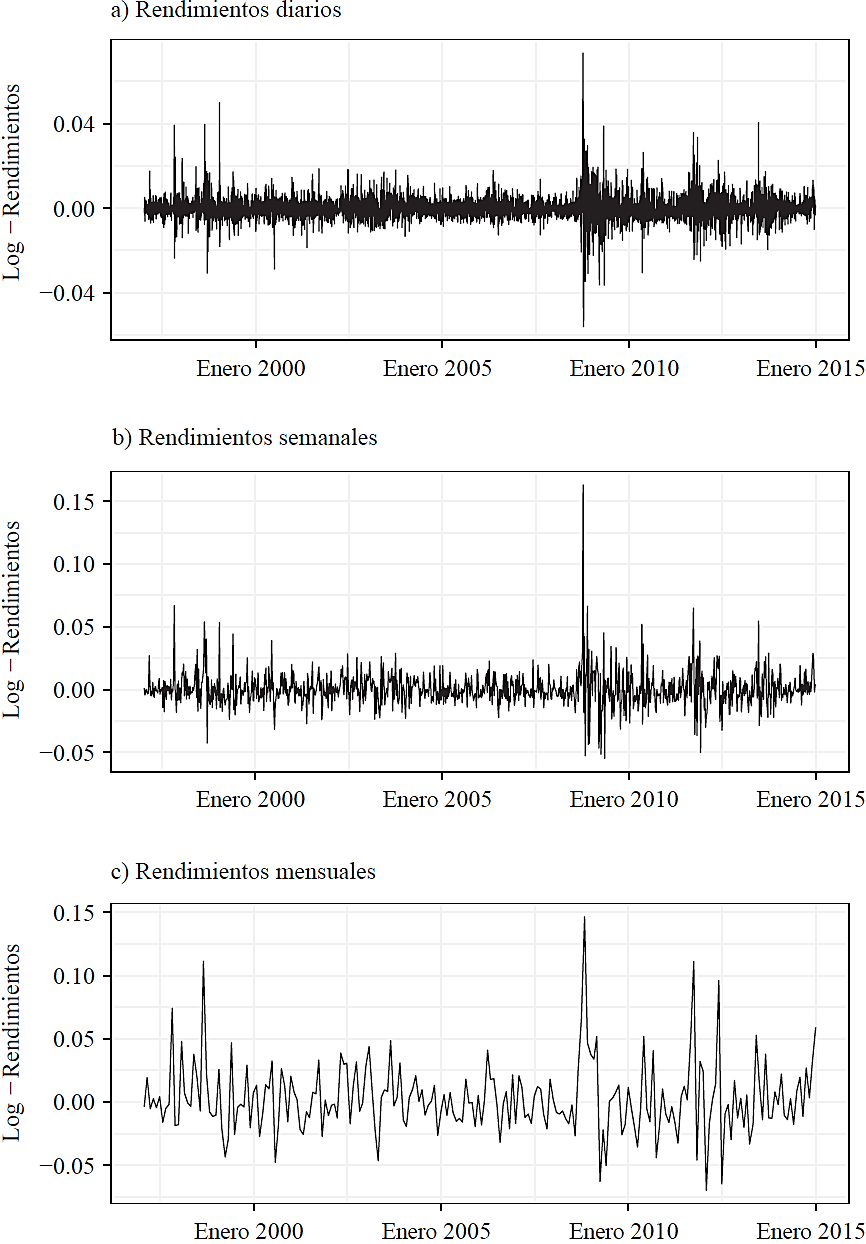
Fuente: Elaboración propia.
Figura 2 Serie de rendimientos logarítmicos del tipo de cambio para diferentes periodicidades
Estadística descriptiva
En la Tabla 1 mostramos la estadística básica que describe los rendimientos diarios, semanales y mensuales del tipo de cambio. Como puede constatarse, las tres series fluctúan alrededor de cero, y tienen una volatilidad anualizada muy similar: 9.85%, 10.23% y 9.8%, respectivamente.8 Otra característica importante que presentan los rendimientos del tipo de cambio es que la media y la varianza crecen proporcionalmente al tamaño del periodo sobre el cual se calcularon los cambios. En particular, la media y la varianza de los cambios semanales son aproximadamente cinco veces más grandes que la media y la varianza de los cambios diarios, y la media y la varianza de los cambios mensuales son aproximadamente cuatro veces más grandes que la media y la varianza de los cambios semanales.
Tabla 1 Estadística descriptiva de las series consideradas
| Rendimientos | |||
| Diarios | Semanales | Mensuales | |
| Número de observaciones | 4527 | 939 | 216 |
| Media | 0.00014 | 0.00067 | 0.002917 |
| Mínimo | -0.05597 | -0.05475 | -0.069766 |
| Máximo | 0.07333 | 0.16296 | 0.14638 |
| Desviación estándar | 0.00620 | 0.01433 | 0.02830 |
| Asimetría | 0.86245 | 1.90871 | 1.24873 |
| Kurtosis | 13.8389 | 19.60496 | 4.29861 |
| Valor p, test de Jarque-Bera | <0.01 | <0.01 | <0.01 |
Fuente: Elaboración propia.
La Tabla 1 también muestra los coeficientes de asimetría y curtosis. El primero de estos es positivo para las tres series de rendimientos, lo que implica que su distribución es asimétrica a la derecha. Respecto de la curtosis, podemos notar que para todas las series esta se encuentra muy alejada de la curtosis que define a una distribución normal. En particular, la distribución de los rendimientos es leptocúrtica, lo que implica que la curtosis es siempre mayor a 3. Estos resultados son un primer argumento en contra de la normalidad de las series y, por lo tanto, de que el tipo de cambio puede modelarse utilizando un MBG. Estas sospechas se confirman aplicando una prueba de Jarque-Bera: el valor cercano a cero implica que la hipótesis nula de normalidad se rechaza con facilidad.
Estacionariedad e independencia
Antes de calibrar las diferentes series, comprobaremos si los rendimientos del tipo de cambio satisfacen los supuestos implícitos por el MBG y el PVG: a) que son variables aleatorias independientes y b) que son estacionarios con distribución normal y varianzagamma, respectivamente. Para evaluar la independencia de las observaciones, calculamos la función de autocorrelación para las diferentes series de rendimientos. En la Figura 3 se muestran los valores p resultantes de aplicar la prueba de Ljung-Box. Como puede constatarse, solo los datos mensuales pueden considerarse independientes. Esto es porque sus valores p son, generalmente, mayores a 10%.

Fuente: Elaboración propia.
Figura 3 Serie de rendimientos logarítmicos del tipo de cambio para diferentes periodicidades
Por otro lado, para comprobar si las series son estacionarias, aplicamos la prueba de Dickey-Fuller aumentada. En los tres casos, la hipótesis nula de no estacionariedad se rechaza con facilidad. Esto se muestra en la Tabla 2.
Calibración
A pesar de que hemos argumentado en contra del MBG, encontraremos los parámetros asociados a este proceso para poder compararlos con los resultados del PVG. Los parámetros de un MBG pueden encontrarse por el método de máxima verosimilitud. Dado que los rendimientos logaritmicos siguen una función de densidad normal, podemos encontrar su media y su varianza (muestrales) como:
Dado que los rendimientos son calculados suponiendo que la ventana de tiempo, t - q, es igual a uno, podemos deducir de la ecuación (4) que:
Los resultados para las diferentes series de rendimientos se presentan en la Tabla 3.
Tabla 3 Parámetros estimados: movimiento browniano geométrico
| Rendimientos | |||
| Diarios | Semanales | Mensuales | |
| μ | 0.00012 | 0.00057 | 0.00252 |
| σ | 0.00620 | 0.01433 | 0.02830 |
Fuente: Elaboración propia.
Ahora estimamos los parámetros del PVG. El procedimiento se divide en dos etapas (Seneta, 2014). Primero, utilizamos la ecuación (8) para calcular los primeros cuatro momentos de la distribución varianza-gamma a partir de datos muestrales. Si fijamos la ventana de tiempo, t - d, igual a uno tenemos:
donde
Los resultados de estimar los coeficientes del PVG se reportan en la Tabla 4.
Tabla 4 Parámetros estimados para el proceso varianza-gamma
| Rendimiento | |||
| Diarios | Semanales | Mensuales | |
| μ | -0.00087 | -0.00204 | - 0.01024 |
| σ | 0.00575 | 0.01315 | 0.02513 |
| θ | 0.00101 | 0.00272 | 0.01315 |
| v | 0.82672 | 0.962334 | 0.74083 |
Fuente: Elaboración propia.
Comparando las estimaciones de las Tablas 3 y 4, podemos notar que, para las tres series de rendimientos consideradas, el parámetro estimado para la deriva es muy cercano a cero. Sin embargo, la estimación tiene signo positivo para el MBG y signo negativo para el PVG. Esto se debe a que, aunque la estimación en ambos casos involucra a la media muestral,
Como hemos dicho, la ventaja del PVG es que este nos permite considerar el sesgo y el exceso de curtosis que presentan los rendimientos en el mercado cambiario. Como puede constatarse, el sigo del estimador de θ es positivo para las tres series consideradas y su magnitud aumenta con la ventana temporal. El estimador de v también es positivo, pero va decreciendo conforme aumenta la ventana de tiempo. Esto es algo natural, ya que el PVG replica el comportamiento que presentan el sesgo y la curtosis muestrales de las series consideradas.
Comparativa de modelos y bondad de ajuste
En esta sección nos enfocamos al ajuste de los modelos MBG y PVG a los rendimientos del tipo de cambio en México. Comparamos primero las distribuciones normal y varianza-gamma con la distribución empírica de los datos. Luego realizamos algunas pruebas de bondad de ajuste.
Distribuciones normal y varianza-gamma
En la Figura 4 mostramos la distribución empírica de las tres series de rendimientos junto con las distribuciones estimadas por una normal y una varianza-gamma. Estas fueron trazadas usando los parámetros de las Tablas 3 y 4, respectivamente. Mostramos, además, el logaritmo de las funciones de densidad.
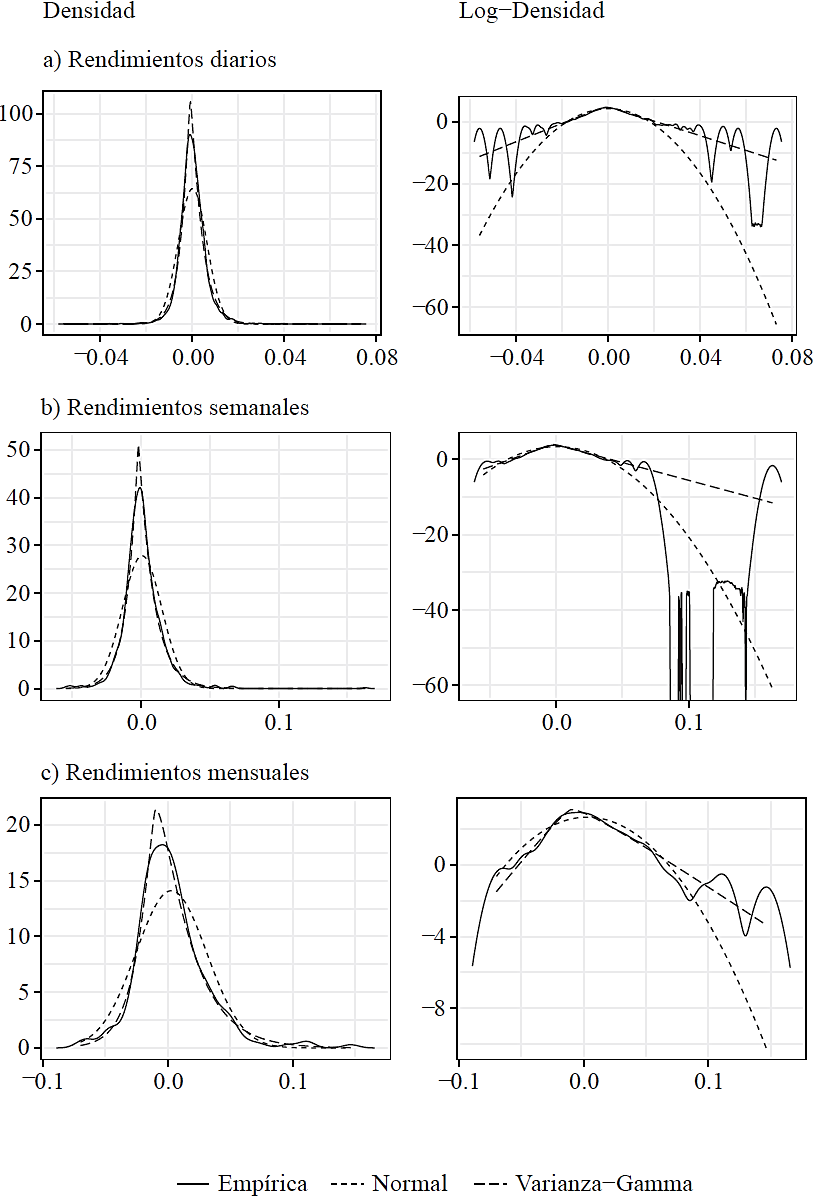
Fuente: Elaboración propia.
Figura 4 Comparación de la densidad empírica de los rendimientos diarios con las densidades estimadas, normal y varianza-gamma
Por una parte, vemos cómo las tres funciones, empírica, normal y varianza-gamma, están centradas cerca de cero y que su ancho es más o menos similar. Esto, a primera vista, indica que el ajuste en términos de la media y la varianza de los modelos MBG y PVG son relativamente buenos.
Si nos enfocamos ahora en la parte central de las distribuciones, podemos notar que el pico de la distribución normal yace por debajo de la distribución empírica y el pico de la distribución varianza-gamma lo hace por encima. Esto quiere decir que la distribución normal subestima la probabilidad de observar rendimientos cercanos a cero y que la distribución varianza-gamma los sobre estima. Esta diferencia; sin embargo, se reduce conforme aumenta la ventana temporal, particularmente en el caso de la distribución varianza-gamma.
En lo que respecta a distancias mayores a ±σ es claro que la distribución varianza-gamma ajusta mucho mejor a la distribución empírica en comparación con la distribución normal. Esto ocurre porque la distribución varianza-gamma tiene la misma proporción de valores que la distribución empírica dentro de tres veces la desviación estándar respecto de la media.
Con la ayuda de las gráficas del logaritmo de la densidad se percibe mejor cómo es el comportamiento de las distribuciones en las partes extremas. Esto es particularmente importante debido a que es esta zona de la distribución la que nos permite determinar de manera apropiada el riesgo de saltos aleatorios en el tipo de cambio. A primera vista, ninguna distribución teórica puede conducirse exactamente conforme a la decadencia de las distribuciones empíricas. Sin embargo, es claro que la distribución varianza-gamma tiene un mejor ajuste, especialmente en el extremo izquierdo. También podemos constatar que las distribuciones empíricas son muy volátiles en sus extremos, particularmente en el derecho. Esto provoca que el ajuste de la distribución varianza-gamma no sea tan bueno en los cambios extremos del tipo de cambio positivos. Indiscutiblemente, la distribución normal no puede corresponder con la proporción de valores en las colas de las distribuciones empíricas, debido a que casi el total de la probabilidad está contenida en el intervalo de ± tres veces la desviación estándar respecto de la media.
Otro aspecto importante que debe considerarse es el ajuste respecto de la asimetría y al sesgo. Cabe resaltar que, debido a sus propiedades, la distribución normal no puede describir la asimetría positiva que tienen los cambios del dólar. Por el contrario, se aprecia que la distribución varianza-gamma asigna mayores probabilidades al extremo positivo que al negativo, razón por la cual la cola del lado derecho de la distribución luce más abultada que la cola del lado izquierdo. Esto se puede ver porque que el logaritmo de la densidad tiene una pendiente relativamente más alta para los valores negativos que en los positivos. Es claro, entonces, que la distribución varianza-gamma ajusta mejor al sesgo de la distribución empírica.
Concluimos entonces que el MBG tiene, en general, un pobre desempeño describiendo los movimientos del mercado cambiario. Sin embargo, este resultado parece ser un poco sorprendente, especialmente si consideramos los rendimientos mensuales. Esto es debido a que los cambios en el precio de algún activo financiero sobre un cierto periodo es el resultado de sumar un infinito número de transacciones del mercado realizadas sobre ese periodo. Como las transacciones se consideran variables aleatorias independientes, el teorema del límite central implica que los cambios tienden a parecerse cada vez más a una distribución normal conforme aumenta el periodo de tiempo. Claramente, para el tipo de cambio USD/MXN esta característica no se cumple, al menos para la ventana de tiempo considerada.
Las diferencias entre las distribuciones teóricas y empíricas también pueden observarse en las gráficas de cuantiles de la Figura 5. Para la distribución normal podemos notar cómo los cuantiles teóricos dibujan una línea ondulada en el centro, lo que evidencia que el ajuste de las frecuencias relativas esperadas en esta área es muy diferente al de las frecuencias de la distribución empírica. Además, observamos que los extremos de las gráficas de cuantiles están muy dispersos respecto de la línea de referencia. Esto implica que la distribución normal no puede ajustarse a las colas de la distribución empírica.
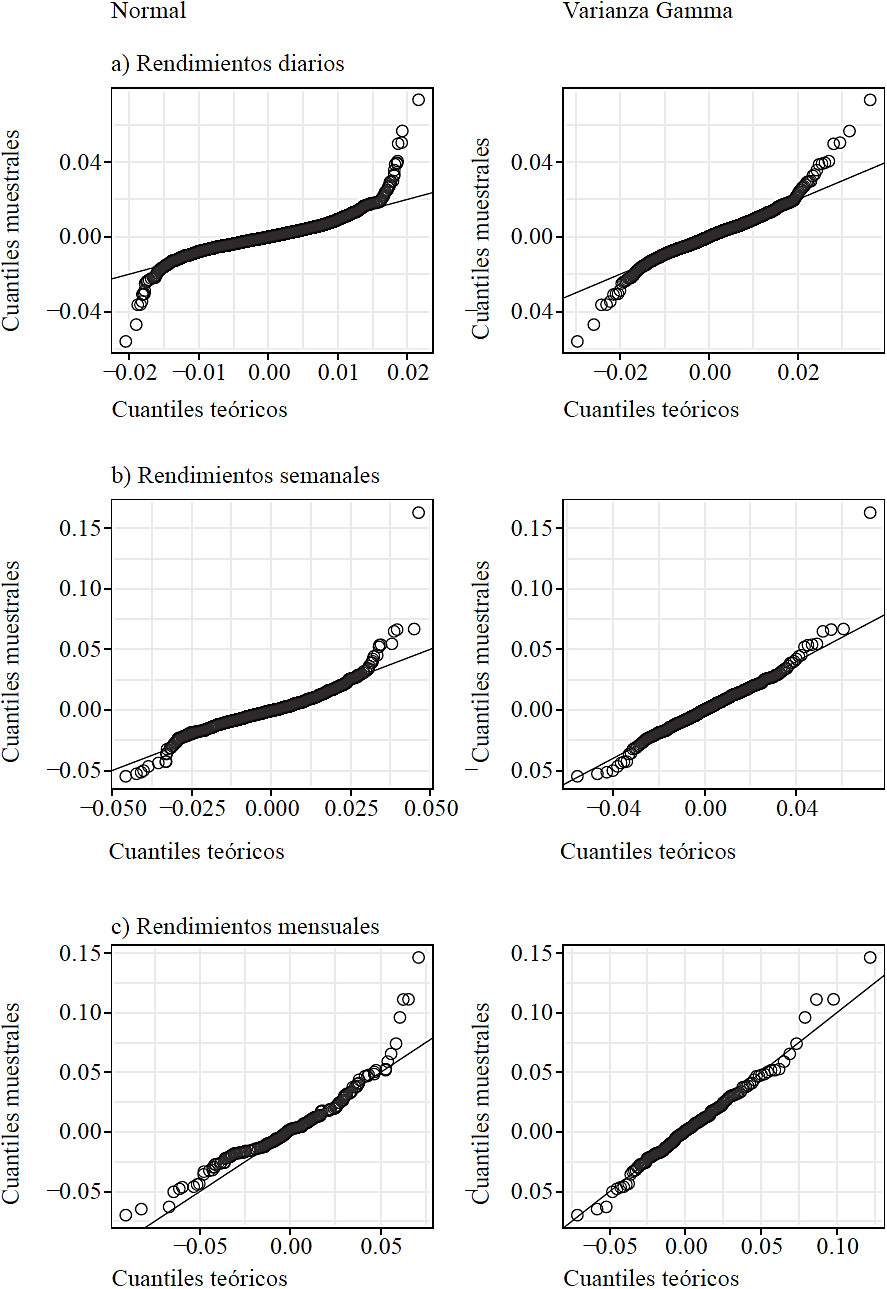
Fuente: Elaboración propia.
Figura 5 Gráficas de cuantiles para las densidades estimadas, normal y varianza-gamma
Si observamos ahora las gráficas de cuantiles de la distribución varianza-gamma, resulta claro que el ajuste en el centro de la distribución es relativamente plano. Además, los extremos no aparecen tan dispersos. A pesar de algunos puntos aislados en los extremos -particularmente en la parte superior derecha de las gráficas-, podemos constatar que el ajuste a los datos es mucho mejor comparado con el ajuste de la distribución normal.
Pruebas de bondad de ajuste
En esta sección seguimos la recomendación de Göncü, Oguz Karahan y Umut Kuzubas (2013) y realizamos varias pruebas de bondad de ajuste. En particular, realizamos las pruebas Chi-cuadrada, Anderson-Darling y Kolmogorov-Smirnov.
Aplicamos la prueba Chi-cuadrada para la bondad de ajuste dividiendo el rango de log-rendimientos en m subintervalos. Para poder comparar el ajuste de todas las series analizadas, consideramos los subintervalos definidos por:
El estadístico de la prueba es:
donde f.obi se refiere a la frecuencia de los datos en la celda i y f.esi es la frecuencia esperada de la distribución en la celda i. La frecuencia esperada se obtiene de multiplicar la probabilidad de que los valores de la distribución caigan dentro de la celda i por el tamaño de la muestra, n. El estadístico tiene distribución Chi-cuadrado con m -1 - k grados de libertad, donde k es el número de parámetros que se estimaron a partir de la muestra.
El estadístico Anderson-Darling está basado en la distancia entre alguna función de distribución acumulada y la distribución acumulada empírica. Este se define como:
donde F(∙) denota una función de distribución acumulada teórica y zi, con i = 1, 2, ..., n, es la serie de datos ordenados de menor a mayor. El estadístico A2 puede compararse con los valores críticos de la distribución normal en Stephens (1974).
Finalmente, el estadístico de Kolmogorov-Smirnov se calcula como:
donde F(∙) es una función de distribución acumulada teórica. Como lo indica Göncü, Oguz Karahan y Umut Kuzubas (2013), el estadístico KS nos ayuda a cuantificar el ajuste de la distribución varianza-gamma en relación con una distribución normal.
Presentamos en la Tabla 5 los resultados de aplicar las diferentes pruebas. Como puede verse en la Tabla 5, los estadísticos de la Chi-cuadrada son claramente inferiores bajo la distribución varianza-gamma. Sin embargo, los valores p nos indican que no podemos concluir que los rendimientos diarios y semanales sigan alguna de las distribuciones propuestas. Para los rendimientos mensuales del tipo de cambio, la prueba Chi-cuadrado es concluyente, el altísimo valor p es indicativo del buen ajuste del PVG.
Tabla 5 Resultados de diferentes pruebas de bondad de ajuste
| X2 | A-D | K-S | ||||
| Rend. | Normal | VG | Normal | VG | Normal | VG |
| Diario | 5.18e+12 | 1374.7 | ∞ | 2.69 | 0.07 | 0.018 |
| (<0.01) | (<0.01) | (<0.01) | (0.039) | (<0.01) | (0.1) | |
| Semanales | 401.79 | 16.78 | ∞ | 0.41 | 0.09 | 0.02 |
| (<0.01) | (0.024) | (<0.01) | (0.84) | (<0.01) | (0.85) | |
| Mensuales | 20.41 | 1.39 | 3.59 | 0.25 | 0.1 | 0.03 |
| (<0.01) | (0.98) | (0.014) | (0.97) | (0.023) | (0.99) | |
Nota: Los valores p se muestran entre paréntesis.
Fuente: Elaboración propia.
Una historia similar puede deducirse de las pruebas Anderson-Darling y Kolmogorov- Smirnof. La única diferencia es que estas pruebas indican que, además de la serie de rendimientos mensuales, tampoco podemos rechazar la hipótesis nula de varianza-gamma en el caso de los rendimientos semanales. En ambos casos, el valor p de la prueba es superior a 80%.
Finalmente, es evidente que los rendimientos se ajustan más a una distribución normal conforme aumenta la ventana de tiempo para el cual fueron calculados. Esto puede observarse ya sea viendo la reducción en el valor del estadístico o en el aumento del valor p de la prueba. Sin embargo, este aumento no es suficiente para concluir que el tipo de cambio en México siga un MBG.
Valor en riesgo y backtesting
El valor en riesgo (VaR) es una técnica estadística que nos permite medir el riesgo financiero de una inversión. Indica la probabilidad de sufrir una determinada pérdida durante un periodo de tiempo determinado. El VaR se utiliza para evaluar el comportamiento extremo en los datos financieros (Jorion, 2006). Además, también se puede utilizar para medir qué tan bien ajusta una distribución a los datos en las colas. Formalmente, el VaR se define como:
donde x son los log-rendimientos, F(∙) su función de distribución acumulada y 0 < p < 1.
El cálculo del VaR es de suma importancia para las instituciones financieras debido a que puede anticipar el capital económico requerido para hacer frente a pérdidas no anticipadas. Además, Beling, Overstreet y Rajaratnam (2010) han demostrado que, según el marco de Basilea, existe un impacto negativo en los beneficios de las instituciones financieras debido a una incorrecta estimación del VaR en cualquier dirección. Cuando del tipo de cambio se refiere, el VaR permite a los bancos, por ejemplo, seleccionar un método adecuado para la determinación de su capital regulatorio bajo la exposición al riesgo de mercado (Swami, Pandey & Pancholy, 2016).
En la Tabla 6 mostramos el VaR de los log-rendimientos del tipo de cambio MXN/USD para diferentes niveles de significancia y los diferentes modelos considerados. Como podemos observar, el VaR calculado a partir de la distribución varianza gamma es siempre más cercano al VaR empírico comparado con el VaR de la distribución normal. Para fortalecer esta conclusión, empleamos la prueba de Kupiec (Kupiec, 1995), la cual nos permite decidir cuál es el mejor modelo para calcular el VaR. Específicamente, probamos cuál es la proporción en que se observa una pérdida superior a la predicción del modelo VaR. Esta proporción debe ser, en promedio, no mayor al nivel de significancia. La proporción de excepciones se calcula como:
donde H es el número total de observaciones empleadas en la evaluación. Para evaluar la hipótesis nula que la proporción de excepciones es igual a la esperada teóricamente
el cual sigue una distribución t con H-1 grados de libertad (Kupiec, 1995). En la Tabla 7 mostramos los valores p de la prueba de Kupiec para los datos en la muestra.
Tabla 6 Valor de riesgo de los log-rendimientos de la tasa de cambio MXN/USD para diferentes niveles de significancia
| Rendimientos Diarios | ||||||
| Distribución | 0.1% | 0.5% | 1% | 99% | 99.5% | 99.99% |
| Empírica | -0.0326 | -0.01943 | -0.01488 | 0.01749 | 0.02289 | 0.04005 |
| Normal | -0.01903 | -0.01584 | -0.01429 | 0.01457 | 0.01611 | 0.01930 |
| VG | -0.02218 | -0.01670 | -0.01433 | 0.01713 | 0.02010 | 0.02696 |
| Rendimientos Semanales | ||||||
| 0.1% | 0.5% | 1% | 99% | 99.5% | 99.99% | |
| Empírica | -0.05279 | -0.04462 | -0.03447 | 0.04349 | 0.05415 | 0.07280 |
| Normal | -0.04360 | -0.03623 | -0.03266 | 0.03399 | 0.03757 | 0.04494 |
| VG | -0.05054 | -0.03772 | -0.03219 | 0.04122 | 0.04857 | 0.06561 |
| Rendimientos Mensuales | ||||||
| 0.1% | 0.5% | 1% | 99% | 99.5% | 99.99% | |
| Empírica | -0.06868 | -0.06457 | -0.06096 | 0.10887 | 0.11127 | 0.13884 |
| Normal | -0.08455 | -0.06999 | -0.06293 | 0.06876 | 0.07582 | 0.09038 |
| VG | -0.08105 | -0.06214 | -0.05391 | 0.08980 | 0.10513 | 0.14041 |
Fuente: Elaboración propia.
Tabla 7 Valores p para la prueba de Kupiec para los datos en la muestra
| Rendimientos Diarios | ||||||
| Distribución | 0.1% | 0.5% | 1% | 99% | 99.5% | 99.99% |
| Normal | 1.37e-10 | 1.78e-03 | 4.87e-01 | 2.87e-05 | 3.12e-12 | 2.45e-15 |
| VG | 1.06e-04 | 6.33e-02 | 4.87e-01 | 4.01e-01 | 3.72e-01 | 7.44e-06 |
| Rendimientos Semanales | ||||||
| 0.1% | 0.5% | 1% | 99% | 99.5% | 99.99% | |
| Normal | 4.88e-04 | 7.72e-02 | 8.43e-01 | 2.50e-02 | 5.11e-04 | 6.94e-07 |
| VG | 0.09 | 0.16 | 0.61 | 0.61 | 0.16 | 0.09 |
| Rendimientos Mensuales | ||||||
| 0.1% | 0.5% | 1% | 99% | 99.5% | 99.99% | |
| Normal | 5.11e-01 | 1.41e-01 | 9.12e-01 | 9.72e-02 | 3.06e-02 | 6.86e-05 |
| VG | 0.51 | 0.13 | 0.59 | 0.26 | 0.13 | 0.22 |
Fuente: Elaboración propia.
Como puede verse en la Tabla 7, existe suficiente evidencia para rechazar la hipótesis nula de que la proporción de excepciones observada es igual a la teórica cuando consideramos la distribución normal. Sin embargo, para la distribución varianza-gamma la hipótesis nula no puede rechazarse. Esto es particularmente cierto para los rendimientos semanales y mensuales. Este resultado refuerza nuestros resultados en el sentido de que el VaR puede ser bien aproximado bajo el supuesto de que el tipo de cambio sigue un PVG.
Conclusión
En este artículo analizamos el comportamiento del tipo de cambio del peso mexicano respecto del dólar estadounidense. En particular, modelamos los rendimientos del mercado cambiario utilizando dos diferentes procesos: un MBG -más común en la literatura y más utilizado en práctica- y el PVG. Para hacer lo anterior, calculamos tres series de rendimientos para varias periodicidades: diaria, semanal y mensual.
Nuestros resultados sugieren que la distribución varianza-gamma -implícita en el PVG- ajusta mejor a los rendimientos del tipo de cambio en relación o la distribución normal -implícita en el MBG-. En general, esto ocurre porque la distribución varianza-gamma es capaz de replicar mejor los cambios extremos en el tipo de cambio, particularmente para las series de rendimientos semanales y mensuales. Otro resultado importante es que la distribución normal es incapaz de ajustarse adecuadamente a los datos, incluso para los rendimientos mensuales.
Para concluir lo anterior, hemos calibrado ambos modelos por el método de máxima verosimilitud y hemos aplicado diferentes pruebas de bondad de ajuste. Estas pruebas indican que la hipótesis nula de que los datos siguen un proceso varianza-gamma no puede rechazarse, particularmente en las series semanal y mensual. En cambio, todas las pruebas rechazan la hipótesis nula de normalidad. Esto reviste importancia debido a que en la literatura se suele suponer que los rendimientos de los activos financieros se comportan -al menos para periodicidades altas, como la mensual- como una distribución normal. Como hemos visto, esta distribución falla debido a que no es capaz de capturar otras características de los rendimientos diferentes a la media y la volatilidad. En cambio, el PVG puede capturar algunas características adicionales, tales como el sesgo y la curtosis.
Una aplicación del PVG y, en general, de los procesos de Lévy que se basan en un movimiento browniano subordinado a otro proceso en tiempo continuo, es la valoración de derivados, especialmente las opciones sobre el tipo de cambio. Adicionalmente, el PVG permite a las instituciones financieras calcular más precisamente el VaR, lo cual les útil para anticipar el capital económico requerido para hacer frente a pérdidas no anticipadas. En lo que respecta al tipo de cambio, el VaR permite a los bancos seleccionar un método adecuado para la determinación de su capital regulatorio bajo la exposición al riesgo de mercado. Nuestro análisis muestra cómo existe suficiente evidencia para rechazar la hipótesis nula de que el VaR es calculado correctamente mediante la distribución normal, no así para la distribución varianza-gamma, particularmente para los rendimientos del tipo de cambio semanales y mensuales.











 nueva página del texto (beta)
nueva página del texto (beta)


