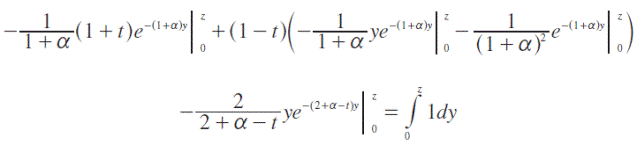Introducción
Cuando se analiza la distribución del ingreso, ya sea a través de un histograma, por resúmenes en cuantiles o por curvas de Lorenz, además de observar la desigualdad existente, se observan niveles de ingreso que muestran una relativa igualdad. Esta aparente igualdad puede crear grupos o polos de ingresos que cumplen ciertas características: Una identificación entre los individuos pertenecientes al mismo grupo y una posible “no compatibilidad” de estos individuos hacia individuos pertenecientes a otros grupos. La literatura en polarización, Esteban-Ray (1994), Esteban-Ray -Duclos (2004), a través de estas observaciones, complementan los resultados de los índices de desigualdad. Hay que notar que si estos grupos no estuvieran identificados o no existieran niveles de ingreso en donde se observe esta igualdad, el concepto de polarización sería el mismo que el de desigualdad. De manera análoga, si los agentes a medir fueran grupos, entonces se podría hablar de una medida de desigualdad entre grupos definida como la polarización misma. Bajo estas dos situaciones tanto desigualdad y polarización coinciden pero, en general, son conceptos diferentes.
Esteban y Ray crean una medida de polarización discreta, que es el resultado de la combinación de alienación con identificación grupal. Con alienación se refieren a la diferencia de un individuo de un grupo con otros individuos de otros grupos; y por identificación se refieren al sentimiento grupal que tienen los individuos hacia otros individuos del mismo grupo. De acuerdo con estos conceptos, la polarización es agrupar a la sociedad en términos de un atributo.
La polarización explica un aspecto que la desigualdad no puede: La potencialidad de conflicto existente en una sociedad cuando se forman grupos en torno a un atributo (Gradín, 2000). Por ejemplo, Pickety (2014) comenta que cualquier individuo podría observar aspectos importantes de cómo está el resto de las personas y la relación de poder que existe entre grupos sociales y con ello proporcionar un juicio distinto de lo que es justo y no, es decir, podría existir una subjetividad fundamental por el concepto de desigualdad, si estas personas fueran líderes de algún grupo, inevitablemente da origen a conflictos políticos. Aún más, El hecho de que la desigualdad disminuya, por algunos factores económicos (Kuznets, 1955), podría reflejar una armonía entre las clases pero, ¿si no se da esta disminución? ¿Cómo medir esta posible no armonía?
Ahora, para saber si la polarización es grave o recomendable tendríamos que saber cómo es el nivel de polarización de la sociedad actualmente, es decir, si la polarización está concentrada en únicamente dos polos. Como el caso mexicano en los años ochenta cuando existían dos partidos: PRI y PRD, aquí era dañina y había que despolarizar creando nuevos grupos. Entonces decir que la sociedad está polarizada no es grave, decir que está altamente polarizada no es recomendable.
Con base en esto, y dado que los conceptos de polarización y desigualdad coinciden en algunos casos, el propósito de este trabajo es ver si existe una política de impuestos que haga coincidir estos conceptos. La literatura (Latham, 1988; Levine-Singer, 1970) muestra que la aplicación de un impuesto proporcional mantiene la desigualdad inalterada; qué significa esto, si el gobierno quiere cambiar la estructura impositiva con algún objetivo: una mejor distribución o un mayor crecimiento (Alesina-Rodrik, 1994), habría que considerar no afectar a la totalidad y mostrar al menos que se sigue perteneciendo a cierto sector de la población. Pero aún más grave, habría que tener cuidado a la hora de la aplicación de esta política de impuestos, es decir, evitar un posible conflicto por el hecho de que la sociedad pague tal impuesto. Este trabajo no pretende reducir la pobreza a través de poner impuestos a los ricos, como menciona Atkinson (2015), más bien es encontrar la manera de que se pague sin crear un posible conflicto, es decir, analizamos las condiciones que debe cumplir la tasa de impuestos para mantener la polarización constante.4
Bajo el supuesto que el ingreso se distribuye de manera exponencial,5 nuestro modelo muestra que bajo una política de impuestos proporcionales, polarización y desigualdad son conceptos diferentes. La relevancia de este resultado se centra en los siguientes hechos: 1) existe una política de impuestos que mantiene la polarización, aplicación de subsidios, diferente a aquella política de impuestos que mantiene la desigualdad, impuestos proporcionales; 2) cuando los individuos están más identificados, las restricciones sobre la política de impuestos para mantener constante la polarización son más estrictas.
El trabajo se estructura de la siguiente forma: analizamos brevemente la relación entre desigualdad y polarización. Después mostramos las medidas analíticas de estos conceptos. Más adelante presentamos el efecto de la política impositiva sobre la desigualdad y la polarización. A continuación hacemos una aplicación a través de la distribución exponencial. Finalmente concluimos con un ejemplo.
Relación desigualdad vs polarización
En esta sección abordaremos los conceptos intuitivos de desigualdad y polarización y la relación existente entre estas a través del atributo ingreso.
Definición 1 (Rocha, 1986): La desigualdad de ingreso o desigualdad económica comprende todas las disparidades en la distribución de ingresos económicos y, entre ellas, muy especialmente la distribución de la renta que procede tanto del capital como del trabajo. El término se refiere normalmente a la desigualdad entre individuos y grupos en el interior de una sociedad, pero también se puede referir a la desigualdad entre países.
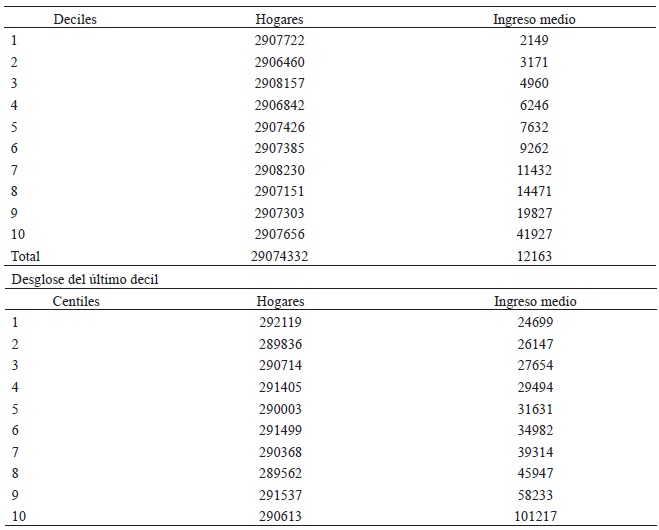
Lo interesante de este concepto es que se están midiendo diferencias individuales, es decir, son individuos, gobiernos, empresas o países que se están tomando en cuenta. Por ejemplo, el Cuadro 1 muestra la distribución de ingresos por deciles para la economía mexicana en 2010, en la cual se observa una gran desigualdad entre la población mexicana. Observe, por ejemplo, que el percentil 99 (última fila del segundo sub-cuadro) de la población mexicana percibe 47 veces más que el primer decil de la población6 (primera fila del primer sub-cuadro). Se quisiera capturar estos aspectos en alguna medida. Una de las más comunes y de manejo accesible, además que es la base de medidas usuales de desigualdad como el coeficiente de Gini o el índice de concentración, es la curva de Lorenz.
Definición 2: La curva de Lorenz mide la relación entre la fracción de la población total que gana un ingreso y, o menor a este, y la fracción del ingreso total ganado por las personas cuyo ingreso es y, o menos (Figura 1)
Por otro lado, observe que tanto en el cuadro como en la figura hay situaciones que merece la pena mencionar. Por ejemplo, en el sub-cuadro 2, los percentiles 92, 93 y 94, tienen un ingreso promedio muy similar, es decir, se observa una aparente igualdad entre estos 3 percentiles a través de un atributo llamado ingreso; el mismo hecho se observa con los percentiles 94, 95 y 96. Además de una posible identificación grupal entre estos, a través del ingreso, hay una diferencia marcada con otros posibles grupos, por ejemplo, los del percentil 98 y 99, y qué decir respecto a la diferencia con los grupos pertenecientes a los deciles 1, 2 o 5, por mencionar algunos.
De la misma forma, en la curva de Lorenz (Figura 1) se observa una aparente igualdad entre individuos pertenecientes a un ingreso similar, el segmento de ingreso A, y otra aparente igualdad entre personas correspondientes al segmento de ingreso B, lo cual podría identificarlos y hacerlos “diferentes” a los demás grupos.
En conclusión, en ambos casos se pueden observar concentraciones de personas que podrían identificarse a través de un atributo y además se “consideren” diferentes al resto de la población. Esto abre camino al concepto de polarización.
Definición 3: La polarización es una medida de agrupación en relación con un atributo, basada en dos conceptos: la identificación de individuos dentro de un grupo y la “diferencia” de estos grupos hacia otros.
Esteban, Ray y Duclos definen por Alienación la diferencia existente entre los grupos identificados. Para que la alienación sea trasladada en voz efectiva, acciones o protestas, los individuos deben identificarse con otros individuos en la sociedad. A esta voz efectiva le llaman alienación grupal, que es la relación conjunta de los dos sentidos, también llamada: marco alienación-identificación.
De acuerdo con esta definición y con base en la Figura 1, podemos decir que la sociedad está polarizada en 5 grupos: 1) el primer grupo antes del ingreso A, 2) los de ingreso A, 3) los de ingreso entre A y B, 4) los de ingreso B y 5) los de ingreso mayor a B. Ahora, si el atributo fuera religión tendríamos una sociedad polarizada en 6 grupos, por ejemplo: 1) católicos, 2) protestantes, 3) evangélicos, 4) musulmanes, 5) budistas y 6) ortodoxos. O si el atributo fuera por grupo étnico (Montalvo-Reynal, 2005) tendríamos: indígenas, arios, negros, orientales, etc.
Es importante mencionar que una sociedad altamente polarizada podría caer en cuestiones de conflictos. Por ejemplo, lo que sucedió en la posguerra, cuando el mundo se dividió en capitalistas y comunistas dando paso a la guerra fría. O simpatizantes políticos cuando solo existen dos fuerzas: republicanos, independientes.
De lo anterior, es importante que la sociedad no esté altamente polarizada. En nuestro caso, si existiera un orden representado por el nivel de polarización a través del ingreso, habría que ser cuidadoso en la aplicación de impuestos para que este orden no se altere, es decir, que la polarización se mantenga. Además de conservar este orden, estamos interesados en hacer una comparación con el nivel de desigualdad a través de la aplicación de impuestos. Para hacer esta comparación se necesita formalizar los conceptos que a continuación hacemos.
Medidas analíticas de la desigualdad y polarización
Deducción de la curva de Lorenz y su aplicación
Introduzcamos variables económicas para la construcción analítica de la curva de
Lorenz. Sean
Bajo el supuesto de que las personas se distribuyen como el ingreso, podemos
suponer que
Por otro lado, sea h(y) la fracción del ingreso total ganado por las personas cuyo ingreso es , o menos, definida por:
donde
La definición 1 nos dice que la curva de Lorenz relaciona las variables h y F. De manera directa no podemos encontrar la relación, por lo que expresaremos la curva de Lorenz de forma general en términos de la distribución de ingresos f(y), y esto es posible debido a que definimos F y h en términos de f(y). Así, la forma paramétrica de la curva de Lorenz es:7
donde h(y) = h(F
-1
(q)), con
Aplicaremos la expresión (1) para hacer comparaciones entre distribuciones de ingresos. Esto es, si dos distribuciones tienen asociadas sus respectivas curvas de Lorenz y no se intersectan, entonces ellas pueden ordenarse sin problema en términos de funciones de bienestar,8 lo que se cita en la siguiente definición (Atkinson 1970):
Definición 4: (Dominancia de Lorenz (LD)): Una economía representada
por su distribución de ingresos f
1 (x) muestra menor desigualdad en el sentido de
Lorenz que una economía representada por f
2 (x) si sus respectivas curvas de Lorenz
h(F
1
(x)) y h(F
2
(x)) satisfacen la condición
Si las curvas de Lorenz
Deducción de la medida de polarización
Deduciremos el concepto de Polarización y analicemos qué ocurre con ella cuando se aplica una política proporcional de impuestos. De entrada quisiéramos mantenerla, para que el orden no se altere. Esto es, una vez que la sociedad se agrupa no conviene dividir a la sociedad en dos polos:9 los que pagan y los que no pagan. Así, el objetivo se restringe a ver qué condiciones debe satisfacer la tasa de impuestos proporcionales para no ocasionar un posible conflicto social.
De acuerdo a la definición 3, habría que integrar el concepto de identificación grupal como la diferencia entre los grupos, respecto a un atributo. Así, Esteban y Ray deducen la forma discreta de la medida de Polarización en la siguiente expresión:
para algunas constantes
Como el objetivo es encontrar el efecto de una política impositiva en la
desigualdad y la polarización a través de una distribución de ingresos, el
atributo de agrupación será el ingreso disponible. Debido a que la tasa de
impuestos está definida en un intervalo continuo
El sentimiento de alienación de un individuo, localizado en el ingreso
x, hacia otro localizado con ingreso y se
llama función de alienación y es la diferencia de un individuo hacia el otro
denotada por
Esteban, Ray y Duclos demuestran que expresión (2) se puede reducir a:
con α ϵ 0,.25,1.
Efecto de política impositiva sobre la desigualdad y polarización
Analizaremos el efecto de una política de impuestos proporcional al ingreso sobre la desigualdad y la polarización representadas por (1) y (3) respectivamente.
Política impositiva y desigualdad
Latham muestra que la desigualdad en el ingreso, para cualquier función de distribución, se mantiene inalterada cuando se aplica una función de impuestos que es proporcional al ingreso. En esta sección mostramos formalmente este hecho. Así, Sean f 1 (x) la distribución de ingresos antes de impuestos y f 2 (x) la distribución de ingresos después de impuestos, así lo mostrado por Latham en relación con la definición 4 se puede escribir de la forma siguiente:
Proposición 1: f 1 (x) es equivalente en el sentido de Lorenz (LE) a f 2 (x) si y sólo si la función de impuestos es proporcional al ingreso.
Ahora, sean t(y) la función de impuestos,
Proposición 1.1: La desigualdad bajo f(y) es la
misma que la desigualdad bajo f(x(y)) si y sólo si la función
de impuestos es proporcional al ingreso, esto es, t(y)=τ con
Política impositiva y polarización
Con el objetivo de utilizar una medida más detallada para aplicar una política
impositiva, notar que el factor
introduciendo la anterior en (3),
Descomponiendo e integrando por partes, se obtiene:
donde,10
En principio se quiere hacer una comparación entre desigualdad y polarización, a través de una política impositiva. Ya se observó en la proposición 1.1 que una política impositiva proporcional mantiene la desigualdad para cualquier tasa de impuestos; se quiere ver ahora qué condiciones deben cumplirse sobre esta política para mantener la polarización y con ello hacer una comparación entre las medidas.
Teorema: Si la polarización está definida como en (4) y el ingreso
disponible es y(1-t) para
Demostración: En Andrade (2012) se demuestra una versión del teorema del cambio de variable aplicado a distribuciones de ingreso, utilizamos el resultado para mostrar que:
Así, f(y)=(1-t)f(y(1-t)), sustituyendo en (4) se tiene:11
Para encontrar el cambio en la polarización respecto a la tasa de impuestos, derivamos P α (F,t) respecto a t, esto es,
Como el objetivo es mantener la polarización antes y después de la aplicación de
impuestos hacemos
Podemos quitar la integral y hacer la igualdad sólo para los integrandos,12 esto es,
transponiendo términos:
Desarrollando el primer miembro:
lo anterior implica que:
la expresión anterior es una ecuación diferencial separable, que al resolverla nos queda:
aplicando leyes de logaritmos tenemos:
finalmente, aplicando la función exponencial y transponiendo se tiene el resultado buscado:
Efecto de la política impositiva para el caso particular de una distribución exponencial
La distribución exponencial
De acuerdo con la información mostrada en el Cuadro 1, se nota claramente un comportamiento sesgado a la derecha, esto es, se observa un alto porcentaje de individuos con ingresos bajos, alrededor del 40%, y un gran porcentaje de personas con un ingreso menor respecto al ingreso promedio13 (casi el 80% de las personas), además de un porcentaje muy bajo de individuos que tienen un alto nivel de riqueza.14 Este tipo de distribuciones sesgadas se representan en general por distribuciones gama (Figura 2). De esta distribución se desprenden distribuciones particulares como la x 2 y la exponencial. Optamos por la distribución exponencial sin pérdida de generalidad, debido a que facilitará la deducción analítica del efecto impositivo sobre la desigualdad y polarización, además, sin perder la particularidad del sesgo que representa una sociedad como la mexicana.15
Así, para una economía con un ingreso promedio µ la distribución exponencial es:
Efecto sobre la desigualdad
En la proposición 1.1, notar que la desigualdad se cumple para cualquier función de distribución, en particular se cumple para una distribución exponencial. En Andrade (2012) se muestran los detalles del impacto de un impuesto sobre la desigualdad cuando la distribución de ingresos es una distribución exponencial. Lo cual citamos en el siguiente resultado:
Corolario: Si el ingreso se distribuye exponencialmente, la
desigualdad en el ingreso antes y después de la política de impuestos es la
misma si, y sólo si, la política consiste en la aplicación de una función de
impuestos proporcionales, esto es,
t(y)=τ y con
Aplicación sobre la polarización
El corolario anterior muestra que la desigualdad se mantiene para cualquier valor
de
Proposición 2: Dada la medida de polarización, si la política fiscal consiste en aplicar un impuesto proporcional y el ingreso se distribuye exponencialmente, entonces la tasa de impuestos que mantiene la polarización satisface:
Demostración: Encontremos las expresiones g(y(1-t)) y f(y(1-t)) para una distribución exponencial con media µ. Esto es, sabemos que g(y(1-t)) cumple con,
g(y(1-t)) = E(y(1-t))+ y(1-t)(2F(y(1-t))-1)-2µ * (y(1-t))
Donde,
y
ahora, dado que el operador esperanza es lineal, tenemos:16 E y t t E y t µpor otro lado, la función de distribución acumulativa es:
la media truncada es:
Sustituyendo lo anterior en g(y(1-t)):
reduciendo términos,
Por otro lado, aplicando el teorema de cambio de variable se tiene:
Elevando ambos miembros a la 1+α y sustituyendo la distribución exponencial, nos queda:
Así, sustituyendo (7) y (8) en (5):
reduciendo términos , tenemos finalmente:
La expresión anterior muestra las condiciones que debe cumplir la tasa de impuestos para mantener constante la polarización.
Ejemplo
En el siguiente ejemplo mostramos que las condiciones citadas en la proposición 2 no son las mismas que las condiciones establecidas para mantener constante la desigualdad.
Ejemplo: Dados los resultados en el teorema y la proposición 2, si la
renta promedio de los individuos y el valor máximo del ingreso son17µ=1
z=50 respectivamente, y para cualquier valor de
En efecto, sustituyendo el valor de en (6) tenemos:
integrando sobre todo el dominio de y, de 0 a z, nos queda:
evaluando las integrales,
sustituyendo z=50 y reduciendo términos, tenemos:
Resolviendo la anterior para18t,
El Cuadro 2 y la Figura 3 muestran los resultados de y para diferentes valores de α ϵ [.25, 1]
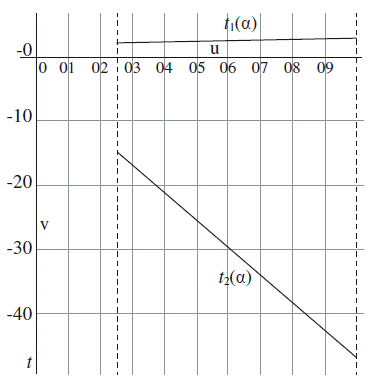
Fuente: Elaboración propia
Figura 3 Valores de la tasa de impuestos en función del coeficiente de identificación grupal
Cuadro 2 Efecto del nivel de identificación sobre las políticas fiscales
| α: Nivel de identificación | t1(α): Política impositiva | t2(α): Política subsidiaria |
| 0.25 | -34.7958 | 2.2125 |
| 0.3 | -36.832 | 2.2624 |
| 0.35 | -38.8879 | 2.3124 |
| 0.4 | -40.9623 | 2.3623 |
| 0.45 | -43.0541 | 2.4123 |
| 0.5 | -45.1622 | 2.4622 |
| 0.55 | -47.2857 | 2.5122 |
| 0.6 | -49.4237 | 2.5621 |
| 0.65 | -51.5753 | 2.6121 |
| 0.7 | -53.7398 | 2.6621 |
| 0.75 | -55.9166 | 2.712 |
| 0.8 | -58.1049 | 2.762 |
| 0.85 | -60.3041 | 2.812 |
| 0.9 | -62.5137 | 2.8619 |
| 0.95 | -64.7331 | 2.9119 |
| 1 | -66.9619 | 2.9619 |
Fuente: Elaboración propia.
El ejemplo nos muestra que para un valor fijo del ingreso z y su respectivo ingreso promedio µ, los valores de t que mantienen la polarización están fuera del intervalo (0,1) a diferencia de los valores t ∈ (0,1) que mantienen la desigualdad, esto es, las condiciones sobre las funciones de impuestos no coinciden. Además, cabe notar que conforme los individuos se sienten más identificados, las restricciones sobre la tasa de impuestos son más estrictas. Más aún, podemos concluir que no existe una política impositiva proporcional al ingreso que mantiene la polarización.
Conclusión
La diferencia entre desigualdad y polarización es el agente económico a estudiar; en la desigualdad, el agente es el individuo y en la polarización, el agente es un grupo de individuos. De hecho, se podría definir la polarización como la desigualdad entre grupos. Más aún, para un valor específico del parámetro de identificación, la expresión de polarización se reduce al índice de Gini, que no es más que la polarización sin fuerza grupal y la medida clásica de desigualdad.
En este artículo se mostraron las diferencias entre las condiciones para que una función de impuestos mantenga la desigualdad y la polarización. Los resultados muestran que no hay condiciones para mantener la desigualdad, independientemente de cualquier distribución. En cambio, para mantener la polarización constante a través de una política impositiva proporcional al ingreso si hay condiciones sobre la tasa que se aplica, mostramos lo anterior a través de una distribución exponencial.
Así, si se desea mantener constante la polarización, la política fiscal a implementar es un subsidio, el cual aumenta conforme los individuos se sientan más identificados. Resaltando con esto que el parámetro de identificación grupal es importante en el concepto de polarización y es un término que hace más relevante la diferencia entre estos dos conceptos. En resumen, se muestra que las políticas son diferentes para mantener constantes tanto desigualdad y polarización.
El aporte a la literatura, a través de nuestro modelo, es que al querer mantener el orden, representado por el nivel de polarización existente, y al mismo tiempo cambiar la estructura fiscal, es posible hacerlo si se consideran políticas fiscales negativas, como el caso de los subsidios. Además, si existiera una reforma política con algún fin, como el caso de México, habría que tomar en cuenta el grado de polarización existente, es decir, una política proporcional no es factible cuando la distribución de ingresos es sesgada como el caso de México, quizá una política progresiva traiga menos consecuencias drásticas.
El artículo abre la posibilidad a examinar otras distribuciones del ingreso, diferentes a la distribución exponencial. Aunque se justifica de manera correcta dicha distribución, existen economías no necesariamente sesgadas que pueden representarse con otras distribuciones de ingreso, como distribución Pareto o distribución Beta. También otorga la posibilidad de examinar, mediante estudios econométricos, la relación entre estos conceptos para la economía mexicana, además de hacer comparaciones con otras economías como la de Brasil, india, Rusia, entre otros países, que pudieran mostrar las mismas características que la mexicana, lo cual se analizará en estudios posteriores.











 nueva página del texto (beta)
nueva página del texto (beta)