Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
EconoQuantum
versión On-line ISSN 2007-9869versión impresa ISSN 1870-6622
EconoQuantum vol.7 no.2 Zapopan ene. 2011
Artículos
Eficiencia industrial en las regiones de México
Genaro Aguilar Gutiérrez1
1 Profesor en la Sección de Estudios de Posgrado e Investigación de la Escuela Superior de Economía del Instituto Politécnico Nacional.
Recepción: 28/06/2010.
Aceptación: 12/01/2011.
Resumen
Esta investigación utiliza la metodología de Función de Producción de Frontera estocástica (FPF) al análisis de eficiencia técnica de empresas industriales en 91 municipios de México. Los datos cubren el período 2006/2008 a nivel de firmas, por rama de actividad económica. Los resultados indican que la frontera estocástica se contrajo en la rama de minerales no metálicos, se estabilizó en las ramas de calzado, confección y textil y tuvo desplazamiento suavemente expansivo para el sector de muebles. Una conclusión es que todos los sectores exhiben una tendencia al aumento de los niveles promedio de ineficiencia técnica. La concentración industrial, incentivos salariales y niveles de escolaridad son factores explicativos del desempeño industrial. No obstante, modelos más generales y la inclusión de nuevas variables en la ecuación de ineficiencia son procedimientos necesarios para obtener estimaciones más robustas.
Palabras clave: eficiencia industrial, desarrollo regional e industrial y modelo de frontera estocástica.
Clasificación JEL: L16, C23, L6.
Abstract
This study employs the Stochastic Frontier Production Functions to some Mexican industrial sectors using firm level data. The results show diversity in sector performance for 2006/2008, but indicate that the majority of the sectors records negative shifts of their performance. The coefficient indicates that the value of output has tended to increase by a small, but insignificant, rate over the three–year period. The estimated coefficients in the inefficiency model are of particular interest to this study: the results indicate that the model, involving a constant term, industrial concentration, dummy variable, schooling and year of observation, is a significant component in the stochastic frontier production function. Further theoretical and applied work is obviously required to obtain better and more general models for stochastic frontier and technical inefficiency effects associated with the analysis of panel data.
Introducción
Tenemos como objetivo analizar aquí, bajo la óptica de la eficiencia técnica, el desempeño económico de firmas –sectorialmente especializadas–en el período 2006/2008 y discutir posibles determinantes estructurales de los resultados obtenidos. Nos proponemos, con este ejercicio, implementar una metodología que posibilite una mejor comprensión del desempeño de esas especializaciones, toda vez que diferencias en los niveles de eficiencia técnica de las empresas son relevantes en la orientación de políticas públicas cuando se logra identificar los factores que contribuyen a esos resultados.
La naturaleza aproximativa de este estudio justifica la elección de un subconjunto de 5 actividades sectoriales –un subsector, dos ramas y dos subramas del Sistema de clasificación Industrial de América del Norte–, siendo la metodología de análisis aplicable a una base de datos más amplia. La primera etapa del ejercicio busca identificar las aglomeraciones sectorialmente especializadas a nivel municipal, para los 91 municipios industrialmente más importantes, en esas actividades, del país; la segunda etapa calcula las eficiencias técnicas de los municipios seleccionados a partir de una base de datos y utiliza informaciones sobre las características estructurales de los municipios, que puedan afectar las diferencias observadas en las respectivas eficiencias técnicas.
Después de la introducción se hace una reseña de la teoría de la Función de Producción de Frontera (FPF) y una revisión de los estudios más recientes para el caso de México. Posteriormente presentamos la metodología y la base de datos utilizada. Finalmente exponemos los resultados obtenidos en el análisis empírico y en la quinta parte concluimos el trabajo.
Función de Producción de Frontera (FPF)
Definición
En contraste con la formulación empírica clásica de "función de producción promedio", la llamada Función de Producción de Frontera (FPF) incorpora una restricción según la cual ninguna unidad productiva es capaz de exceder un nivel de producción máximo dado el estado de desarrollo tecnológico. El trabajo pionero de Farell (1957), que calcula la isocuanta unitaria eficiente mediante la utilización de programación lineal y deriva de esa especificación la medida de eficiencia, es el marco inicial de la extensa literatura sobre FPF, que incluye numerosas contribuciones de diversos autores en años subsecuentes (Hjalmarsson et. al, 1996; Kumbhakar y Hjalmarsson,1993; Schmidt y Sickles,1984; Jondrow et. al, 1982; Pitt y Lee 1981); hasta estudios muy recientes (Grassetti, 2009; Kopsakangas–Savolainen y Svento, 2008; Odeck, 2007; Greene, 2005; Oliveira y García, 2004; Gagnepain, 2002; Kumbhakar y Lovell, 2000). Dependiendo de la hipótesis sobre las causas de las diferencias de eficiencia de las unidades productivas, la frontera a ser estimada puede ser clasificada como determinística o estocástica. El modelo es llamado determinístico cuando las diferencias de desempeño de las empresas en relación a la frontera son atribuidas enteramente a la ineficacia técnica. La mayor generalidad del modelo de frontera estocástica está en su posibilidad de distinguir si la divergencia entre un dado nivel de producción y su contrapartida sobre la frontera estocástica se debe a la ineficiencia o a la variación aleatoria en relación a la frontera. Las limitaciones del abordaje de frontera determinística aparecen, por ejemplo, cuando factores como mal tiempo e interrupción en el abasto de insumos, claramente externos al control de la unidad productiva, están presentes y son "contabilizados" como ineficiencia técnica. Ésa es una consecuencia directa –y no deseable– de la especificación de una frontera determinística.
Estudios para México
En el caso de México, en un estudio muy reciente, Becerril et al (2009) estudiaron la disparidad de niveles de eficiencia técnica y la influencia de la infraestructura para la convergencia en términos de eficiencia, del producto interno bruto per cápita en los estados de México. Siguiendo el Modelo propuesto por Battese y Coelli, los autores desarrollaron un Modelo de Frontera Estocástica y realizaron estimaciones de la eficiencia técnica por estados, mostrando que inversiones públicas ayudan a incrementar la eficiencia en el uso de los factores para la producción creando oportunidades para aumentos del crecimiento económico regional. Sin embargo, en ese mismo estudio, los autores encuentran que los niveles de eficiencia industrial por estados del país son sumamente limitados en función de la heterogeneidad estructural del país, lo que conduce a niveles muy diferenciados de eficiencia entre estados del país. Recomiendan, como conclusión, aumentar la inversión pública en infraestructura dando mayor énfasis a los estados más atrasados económicamente.
Álvarez et al (2008) estimaron la eficiencia técnica en la producción privada de las entidades federativas de México durante el período 1970–2003. Siguiendo el Método Envolvente de Datos, los autores muestran un aumento sostenido en los niveles de eficiencia pero con grandes desigualdades regionales debido a las características estructurales de la economía nacional. Así, Álvarez et al (2008) construyen un ranking de la eficiencia técnica de las entidades federativas en 1970 y 2003, concluyendo que las desigualdades regionales en México, en términos de PIB per cápita, en ese período, más que reducirse se ampliaron; por tanto, los autores concluyen que las políticas públicas deben centrarse en la reducción de las desigualdades regionales en términos de ingresos.
Otro estudio interesante es el de Fuentes y Armenta (2006) que, con datos de 133 empresas del sector calzado del municipio de San Mateo Atenco, en el estado de México, midieron cambios en la productividad debidos a transformaciones tecnológicas, derivados de modificaciones en la eficiencia técnica y en la escala de producción para el período 1990–2000. Construyendo el índice de Productividad Total de los Factores de Malmquist (también conocido como índice de Productividad de Malmquist), así como llevando a cabo estimaciones de funciones con la técnica de Análisis Envolvente de Datos, los autores midieron el cambio en la productividad de las empresas analizadas entre dos puntos calculando el cociente de las distancias de cada uno de los puntos en relación con la frontera que representa una tecnología común. Los autores encontraron un crecimiento de 1.2% en la productividad para el grupo de empresas observadas, en el período de análisis, concluyendo que en las empresas analizadas no hubo un cambio tecnológico en los 10 años de estudio (incluso encuentran un ligero retroceso tecnológico en este sector) y que el cambio en la productividad de éstas se debió, enteramente, a cambios en la eficiencia técnica.
Función de Producción de Frontera y la utilidad de datos de panel2
Considerando el contexto de N unidades productivas con datos sobre los respectivos productos e insumos observados durante un período de t años –característico de una base de datos de panel para la industria–, una función de producción de frontera genérica bajo la óptica de un panel de datos puede ser representada de la siguiente forma:3

y ser reescrita como:

Eso es así porque el shock estocástico se compone de dos términos aditivos: el primero, v, que tiene media cero y desviación estándar σ2v; y el segundo, u(> 0) que tiene media μ, > 0 u varianza σ2u.
El componente vi recoge aquellas variaciones en la producción debidas a factores aleatorios que escapan al control del empresario y tiene la interpretación usual de factores cuyos efectos netos se cancelan (en promedio) –caso típico de los errores de medida–, mientras que el componente ui representa la eficiencia técnica en relación a la frontera estocástica y la restricción del nivel de producción a valores iguales o menores que el de la frontera, caracterizando y mostrando, por lo tanto, la ineficiencia técnica.
La especificación de datos de panel presenta dos hipótesis alternativas para modelar el comportamiento específico de cada unidad: i) los efectos individuales ui son constantes específicas de las unidades productivas, lo que es característico del abordaje "efectos fijos"; ii) los efectos individuales ui son términos constantes distribuidos aleatoriamente entre las unidades productivas, lo que configura el abordaje de "efectos aleatorios". La especificación "efectos fijos" puede ser implementada con el estimador de least squares dummy variables (LSDV), mientras la especificación "efectos aleatorios" requiere de mínimos cuadrados generalizados (GLS) o Máxima Verosimilitud (MV), puesto que efectos individuales "aleatorios" ui –diferenciados entre unidades, pero constantes a lo largo del tiempo– provocan correlación serial en los shocks estocásticos de esas unidades. En este estudio, la especificación "efectos fijos" es implementada con mínimos cuadrados ordinarios con variables dummies (LSDV) y la especificación "efectos aleatorios", con máxima verosimilitud. Aunque ambas estimaciones convergen hacia los valores verdaderos de los parámetros con el aumento del número de observaciones (ambos son consistentes), el estimador de MV tiene la ventaja de ser más eficiente (presenta menor dispersión).
Metodología y base de datos
Metodología: Frontera estocástica con datos de panel
Una alternativa al método determinístico de cálculo de la frontera de producción con datos de panel, en el método de estimación de la Eficiencia Técnica, es considerar el término de error unilateral como aleatorio, presentando una distribución particular, no correlacionado con el error de los dos lados (two–sided error) ni con los regresores. Así regresamos a la idea original, en que el término de error está compuesto por dos partes, una específica para cada corte transversal y otra que es el residuo general de la ecuación. El modelo de efectos individuales aleatorios es más coherente con un modelo de frontera de producción estocástica, en que se considera que la razón de la ineficiencia de la unidad analizada tiene por lo menos un elemento ajeno a la decisión de los productores.
Gran parte de los estudios empíricos desarrollados en relación a la producción de frontera no han, explícitamente, construido un modelo para "explorar" los efectos de variables correlacionadas sobre la ineficiencia. Los trabajos que abordan esa cuestión adoptan, en general, un modelo en "dos etapas": en la primera especifican y se estima la frontera y los correspondientes niveles de (in)eficiencia de las unidades productivas; en la segunda analizan los factores que pueden afectar la ordenación de "niveles de eficiencia" obtenida. Sin embargo, como las estimaciones de la eficiencia técnica en la primera etapa son obtenidas a partir del supuesto de que la ineficiencia es independiente, la regresión entre esa medida y sus determinantes es, al menos, conflictiva con la hipótesis de que la eficiencia es independiente e idénticamente distribuida en la frontera estocástica.
Battese y Coelli (1995) proponen modelos para el análisis de la ineficiencia técnica implícita en la función de producción estocástica, en los cuales los parámetros de la frontera y aquéllos del modelo de ineficiencia son estimados simultáneamente. Las especificaciones suponen la existencia de una distribución asociada a los datos de panel de las firmas incluidas en la muestra. Esos autores proponen una especificación en que la eficiencia es expresada como una función de variables específicas, incluida una "tendencia atemporal" y un término aleatorio. Una vez que el modelo proporciona una estructura a la eficiencia técnica, es posible analizar la variación simultánea de la frontera de producción y de la eficiencia, separando así tendencias asociadas a desplazamientos de la frontera (en movimientos de expansión o contracción) de tendencias relacionadas a la diseminación (o no) de la mejor práctica productiva.
Este trabajo sigue la metodología de Battese y Coelli (1995) para analizar el desempeño de unidades productivas en el período 2006–2008 bajo la óptica de la eficiencia técnica. La especificación de esos autores presenta la ventaja de relajar la hipótesis de niveles de eficiencia técnica y frontera tecnológica invariantes en el tiempo. Así:

en donde i = 1,2, N representa a las unidades (firmas) de análisis y t = 1,2, T representa los sucesivos períodos incluidos; yit denota la producción de la unidad i en el tiempo t; xit es un vector (1 x K) de insumos asociados a las unidades de análisis en cada período de observación; β son los k parámetros a ser estimados (observar la constante β0 que representa el intercepto de la frontera de producción); vit son los shocks estocásticos asumidos como independientes e idénticamente distribuidos en una distribución normal con N(0, σ2v) y distribuidos independientemente de uit's, variables aleatorias no negativas que son asociadas a la ineficiencia en la producción; los uit tienen, por hipótesis, una distribución normal truncada con media zitδ y varianza σ2; zit es un vector (1x m) de variables explicativas asociadas a la ineficiencia técnica de las firmas involucradas en el proceso de producción; y δ es un vector de m coeficientes desconocidos a ser estimado.
La eficiencia técnica (uit) es, por hipótesis, una función de variables "explicativas" zit y de un vector de coeficientes desconocidos, δ. Se espera que ese conjunto de variables esté asociado a los desvíos de la producción observada en relación a la frontera estocástica. Los efectos individuales relacionados a la ineficiencia técnica uit pueden ser especificados de acuerdo con:

donde la variable aleatoria wit es definida por el truncamiento de una distribución normal con media cero y varianza δ2 siempre y cuando el punto de truncamiento sea en –zitδ, esto es, wit > –zitδ. Esa hipótesis es consistente con el hecho de que uit posee una distribución truncada no negativa con N(zitδ,σ2).
El supuesto básico de la especificación es que uit y vit son independientemente distribuidos para todo t = 1,2, ... N. La eficiencia técnica para la firma i en el tiempo t de observación es definida por:

Donde la estimación de la eficiencia técnica está basada en un promedio condicionado, dadas las hipótesis del modelo. Es importante observar que si zitδ + wit > zi't' δ + wi't', para i ≠ i', no necesariamente implica zit' δ + wit' > zit' δ + wi't' para t' ≠ t. Se concluye, por lo tanto, que la misma ordenación de las firmas en términos de la eficiencia técnica de la producción no se aplica en todos los períodos.
Las estimaciones simultáneas de los parámetros de la frontera estocástica y del modelo para la ineficiencia técnica emplean en método de Máxima Verosimilitud4 con el supuesto de una distribución truncada para la variable ui. Este trabajo adopta la especificación funcional Cobb–Douglas que, no obstante que es menos flexible en relación a la función Translog, por ejemplo, presenta resultados confiables a la forma funcional en el caso de cambio tecnológico neutro5. La función de máxima verosimilitud es expresada en términos de la varianza de los parámetros σ2s = σ2v + σ2 y r = σ2/σ2s.
Base de datos
La primera etapa de este estudio busca identificar las aglomeraciones sectorialmente especializadas de acuerdo con la metodología presentada en Albuquerque (2000).6 Para ello se utilizaron datos de 2008 de la Secretaría de Economía para el cálculo de cuociente de ubicación (CU) y las unidades son seleccionadas si poseen CU > 1 y porcentaje de empleo en el municipio en relación al total nacional de, al menos, 5%. Las muestras son compuestas por empresas (aglutinadas municipalmente) que destacan (en relación al total nacional) en los siguientes sectores: textil (32 municipios), de confección (23 municipios), calzado (21 municipios), minerales no metálicos (22 municipios) y de muebles (25 municipios).
El análisis de la eficiencia técnica de los municipios seleccionados se fundamenta en la construcción de una función de producción agregada para ese subconjunto de municipios, en que los datos relativos a las variables de producto (Y), trabajo (L) y capital (K) para la función son proporcionados por la Secretaría de Economía para el período 2006–2008,7 referentes a las firmas ubicadas en los municipios en cuestión.
Los datos relativos al valor de la producción son los respectivos ingresos netos por ventas y se refieren a los ingresos por ventas de firmas sectorialmente definidas, presentes en los municipios definidos de acuerdo con el criterio previamente establecido.
En relación al insumo trabajo se utilizaron datos sobre el personal ocupado directamente en la producción industrial: personas efectivamente ocupadas a lo largo de los 12 meses del año de referencia, remuneradas directamente por la empresa en actividades de producción de bienes y servicios industriales (mantenimiento y reparación de equipos industriales o de apoyo directo a la producción industrial). El estudio adopta la compra de energía eléctrica utilizada en la producción como una proxy para el insumo capital, práctica que ha sido observada en la literatura empírica como la "segunda mejor alternativa" en ausencia de informaciones directas sobre el stock de capital.8
Esta investigación, al implementar la metodología estocástica, buscó analizar algunas variables relevantes en la explicación de los diferentes niveles de eficiencia de firmas agrupadas por municipios:9
1. Capital humano (educación): porcentaje de la población –sectorialmente definida–de cada municipio que haya concluido, por lo menos, la secundaria.
2. Concentración industrial: porcentaje de la sumatoria de los ingresos netos por ventas de las firmas del sector, presentes en el municipio como proporción del valor medio del ingreso neto del sector en el año.
3. El indicador de la difusión de la mejor práctica productiva: tanto la frontera de producción como la ecuación de ineficiencia son especificadas para admitir la posibilidad de desplazamiento en el tiempo en su estructura lineal. Un signo positivo en el coeficiente de tendencia temporal de la ecuación de ineficiencia indica un incremento en los niveles medios de ineficiencia entre firmas (municipios) en el período; mientras que un signo negativo significa reducción de esos niveles. Una tendencia estadísticamente significativa de reducción del nivel medio de ineficiencia en un sector es interpretado aquí positivamente como resultado de la difusión de la mejor práctica productiva.
4. Incrementos y/o incentivos salariales: como un intento de captar una posible relación entre incrementos salarios y eficiencia, utilizamos una variable de control dummy = 1 para los municipios que presentan un número de trabajadores remunerados igual o superior al salario promedio del sector en la muestra analizada y variable dummy = 0 para los demás.
Resultados
Modelo estocástico y eficiencia variante, 2006–2008
Este abordaje también adopta la especificación funcional Cobb–Douglas:

siendo y la proxy para la producción, l y k los insumos trabajo y capital, T la tendencia lineal, v y u representan el shock estocástico, como fue descrito en la metodología. Los efectos de la ineficiencia técnica son asumidos como:

siendo T, C, D y E las variables de tendencia lineal, el indicador de concentración industrial, la variable dummy de control para los incrementos salariales y la proxy para el capital humano, respectivamente.
Los resultados muestran que en las estimaciones de las funciones de producción sectoriales, los signos esperados para los coeficientes se cumplen, lo que indica una correlación positiva entre los insumos –capital y trabajo– y el producto. Además de ello, las estimaciones de esos coeficientes son estadísticamente diferentes de cero, a 1% y a 5% de nivel de significancia, para todas las muestras. Tanto la frontera de producción como la ecuación de ineficiencia fueron especificadas para admitir la posibilidad de desplazamiento en el tiempo en su estructura lineal.
Un signo positivo en el coeficiente de tendencia temporal de la ecuación de ineficiencia indica un incremento en los niveles medios de ineficiencia entre firmas (municipios) en el período, mientras que un signo negativo significa una reducción de dichos niveles. Una tendencia estadísticamente significativa de reducción del nivel medio de ineficiencia en un sector podemos interpretarla aquí positivamente como resultado de la difusión de la mejor práctica productiva. En relación a los demás coeficientes de la ecuación de ineficiencia, el signo negativo y estadísticamente significativo sugiere una relación inversa entre la variable explicativa y la ineficiencia. En otras palabras, incrementos en esas variables tienden a disminuir la ineficiencia. Es importante observar que aunque algunos resultados presentan el signo esperado (negativo), no son estadísticamente significativos. Una posible explicación de ese hecho es el corto período de observación.
Los resultados obtenidos para los parámetros de la frontera de cada variable sectorial y para la ecuación de ineficiencia están en los cuadros 1 a 5.
En seguida presentamos una breve discusión de los resultados obtenidos. En el sector de calzado (ver cuadro 1 ) hay estabilidad en la frontera del sector y una tendencia a la dispersión de los niveles de eficiencia (no significativo); los indicadores de concentración industrial y de educación (éste no significativo) presentan signos negativos y contribuyen a la reducción de la ineficiencia. Sin embargo, como un todo entre los años 2006 a 2008, el sector de calzado disminuyó sus niveles de eficiencia técnica. Estos resultados contrastan con los hallazgos de Fuentes y Armenta (2006), quienes encontraron que en el municipio de San Mateo Atenco, en el estado de México, la productividad del sector calzado apenas creció 1.2% en 10 años y que esos incrementos de productividad se debieron a cambios en la eficiencia técnica de este sector, no habiéndose presentado cambios en la tecnología. De estos resultados podemos concluir, preliminarmente, que es muy relevante que la política pública en México debe buscar lograr aumentos más significativos en los niveles de eficiencia técnica en las especializaciones industriales. La literatura internacional muestra que ello se puede lograr a través de dos tipos de políticas clave: las que estimulan la adopción de conocimientos especializados logrando la capacitación de la mano de obra especializada (Learning–by–doing) y mediante políticas de reemplazo de maquinaria y equipo.

En el sector de confección (ver cuadro 2) se observa estabilidad en la frontera y en los niveles de ineficiencia; no hay evidencia de que las variables probadas ejerzan una influencia sobre la ineficiencia en el modelo, pues las variables de control (dummy) y de escolaridad presentan signos negativos (aunque no significativos), lo que sugiere una correlación positiva entre esos indicadores y los de los municipios más eficientes. Así, de la misma forma que en el sector de calzado, es imprescindible que la política pública, emprendida desde la Secretaría de Economía, conduzca programas dirigidos a elevar la eficiencia de sectores clave de la economía.

En el sector de muebles (ver cuadro 3) hay una expansión de la frontera tecnológica del sector y un aumento de la dispersión de los niveles de eficiencia en los municipios. Las estimaciones de los índices de concentración industrial y educación mantienen una relación inversa con la ineficiencia. Los resultados muestran, por lo tanto, que los municipios que poseen mano de obra más calificada y firmas más concentradas industrialmente tienden a ser más eficientes.

En el sector de minerales no metálicos (ver cuadro 4) se puede observar una contracción de la frontera del sector y estabilidad de los niveles de ineficiencia. Estimaciones de incentivos salariales y de niveles de escolaridad están más asociadas a las unidades más eficientes.

En el sector textil (ver cuadro 5) hay cierta estabilidad en la frontera del sector y un aumento de la dispersión de los niveles de ineficiencia. Concentración industrial, incentivos salariales y niveles de escolaridad son variables significativas para explicar el desempeño de las firmas.

Las estimaciones de los niveles medios de eficiencia técnica en los municipios en el período 2006–2008, según el abordaje estocástico –y variantes en el tiempo–, están presentes en los cuadros 6 (7–8–9) a 10.
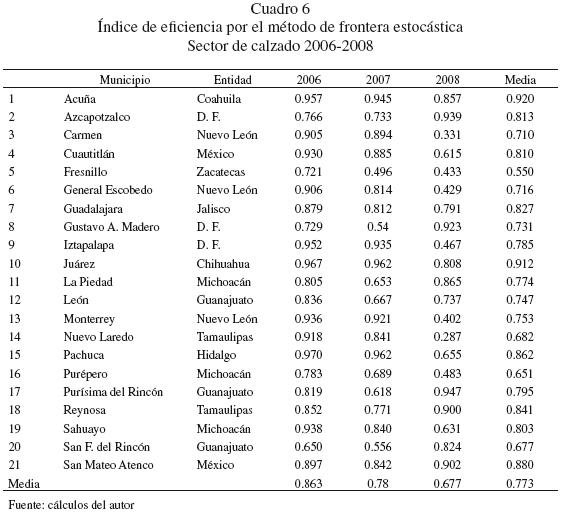


Al realizar los cálculos de los niveles de eficiencia técnica industrial por municipios podemos tener una mejor apreciación de la heterogeneidad estructural de la industria en México. Así por ejemplo, para el caso de la industria del calzado, podemos observar (cuadro 6) que mientras que hay municipios donde las empresas son relativamente muy eficientes (Acuña en Coahuila, Carmen en Nuevo León, Juárez en Chihuahua, y Reynosa en Tamaulipas), existen municipios en los cuales las firmas tienen tales rezagos productivos que las empresas no logran niveles de eficiencia superiores al 50% de su potencial (Fresnillo en Zacatecas y Gustavo A. Madero e Iztapalapa en el Distrito Federal).
Analizando el comportamiento de los niveles de eficiencia por municipios en la industria de la confección podemos observar (cuadro 7) que las empresas agrupadas en este sector en algunos municipios logran niveles muy elevados, superiores al 80% de su potencial, tal es el caso de las firmas de los municipios de El Salto en Jalisco, Atlacomulco y Naucalpan en el estado de México, San Juan del Río en Querétaro y Santa Ana Chiautempan en Tlaxcala; sin embargo, hay municipios del país, especializados fundamentalmente en la confección de prendas de vestir, en los cuales las empresas presentan niveles de eficiencia muy por debajo de su potencial, tal es el caso de las unidades productivas de los municipios de Ecatepec en el estado de México, Jesús María en Aguascalientes, Jiutepec en el estado de Morelos y Matehuala en San Luis Potosí.
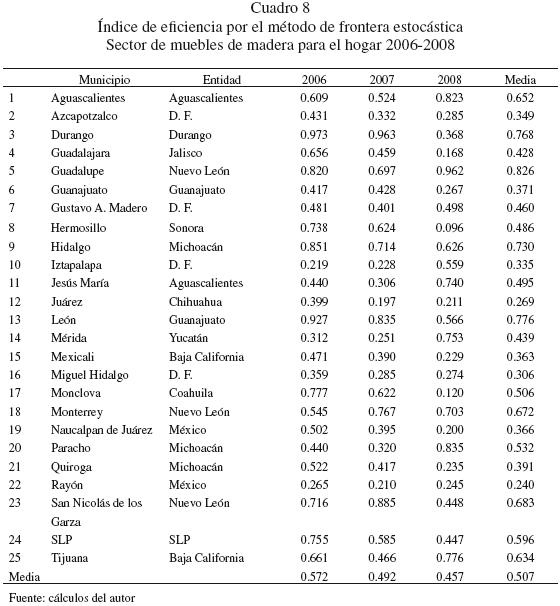
En el sector de muebles de madera vuelve a surgir, una vez más, esa naturaleza estructuralmente heterogénea de la economía mexicana. Así, hay municipios en los cuales la industria es muy eficiente (Aguascalientes en el estado del mismo nombre, Guadalupe en Nuevo León o Tijuana en el estado de Baja California) y, sin embargo, hay municipios en los cuales la industria productora de muebles es muy ineficiente, no alcanzando siquiera el 30% de su potencial, tal es el caso de las empresas ubicadas en los municipios de Rayón y Naucalpan en el estado de México, Mexicali en Baja California, Juárez en Chihuahua y Guanajuato en el estado de Guanajuato (ver cuadro 8).
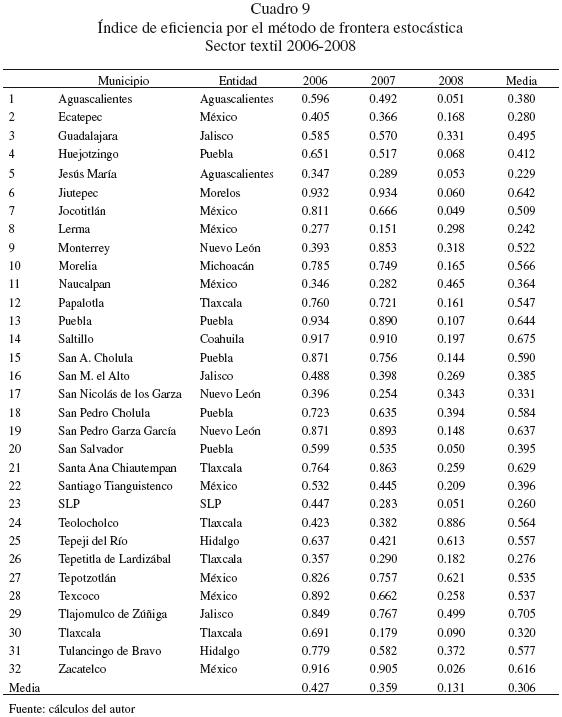
En el sector textil, que tradicionalmente ha sido uno de los sectores claves propulsores de la industria manufacturera nacional, los niveles de ineficiencia son abrumadores. Los resultados del cálculo de la eficiencia técnica muestran que en este sector son escasísimas las empresas en que se estén empleando adecuadamente los factores de la producción. De acuerdo con nuestros cálculos, los mayores niveles de ineficiencia de las empresas textiles de México se encuentran en los municipios de Texcoco, Zacatelco, Jocotitlán, Lerma, Santiago Tianguistengo y Ecatepec en el estado de México, así como Huejotzingo en Puebla, Papalotla en Tlaxcala y Guadalajara en Jalisco (ver cuadro 9). En este sector llama mucho la atención que los niveles de eficiencia técnica disminuyeron abruptamente en los años 2006 a 2008.
La implicación más relevante de la sección anterior es que los niveles de eficiencia técnica industrial en prácticamente todos los sectores analizados ha venido cayendo dramáticamente, debido a lo cual es imperativo que la política pública en México haga un alto en el camino y reconsidere la necesidad urgente de emprender un programa proactivo hacia el sector industrial, definiendo con toda precisión un programa de política industrial que se traduzca en el mediano plazo en mayores niveles de eficiencia industrial. Parece evidente que la falta de inversión en infraestructura para el desarrollo industrial y de inversión en el capital humano está detrás de los niveles de ineficiencia industrial de estos sectores de la industria nacional.
Frontera de producción y eficiencia: Pruebas asintónicas
La relevancia de los efectos de ineficiencia en el análisis de desempeño de los sectores considerados en unidades locales es corroborada para todos ellos en el período 20062008 (ver cuadro 10). Los resultados obtenidos en las pruebas asintóticas de razón de verosimilitud (Loglikelihood–Ratio, pruebas LR)10 indican que la hipótesis nula de ausencia de efectos de ineficiencia es significativamente rechazada para todos los sectores analizados en las diversas especificaciones probadas. El parámetro r, definido como r = σu2/σu2 + σv2 representa la importancia relativa del componente de ineficiencia en el ajuste del modelo. Las estimaciones del parámetro r, por lo tanto, indican si los efectos de ineficiencia son importantes en el análisis de estos sectores. Los coeficientes de r, asumen valores entre 0 y 1. Cuando r  0, los efectos de ineficiencia no tienen relevancia para el análisis del proceso productivo de las firmas de la muestra y, cuando r
0, los efectos de ineficiencia no tienen relevancia para el análisis del proceso productivo de las firmas de la muestra y, cuando r  0, los efectos de ineficiencia son relevantes para dicho análisis.
0, los efectos de ineficiencia son relevantes para dicho análisis.
El Cuadro 10 presenta los resultados obtenidos en las pruebas asintónicas.
Conclusión
El análisis de la eficiencia técnica de las firmas de los sectores aquí estudiados indica que los desempeños técnicos fueron muy heterogéneos en el período 2006–2008 pero, en general, hubo una caída significativa de la eficiencia técnica. No obstante la relevancia de los resultados obtenidos, la opción de trabajar con una base de datos más actualizada y actividades sectoriales más amplias es necesaria.
En relación a la tendencia de la eficiencia industrial en los municipios analizados, podemos observar un movimiento en el sentido de contracción de la frontera tecnológica en el sector de minerales no metálicos, estabilidad en las fronteras de los sectores de calzado, confección y textil y desplazamiento suave en el sentido de expansión del sector productor de muebles. Sin embargo, esos desplazamientos de la frontera fueron acompañados por una tendencia de aumento en los niveles medios de ineficiencia técnica en los diversos sectores y con una mayor dispersión.
De manera general, los indicadores de concentración industrial, incrementos salariales y niveles de escolaridad son factores importantes en el análisis de la eficiencia de las empresas. Estas variables se mostraron relevantes en el análisis de las causas estructurales de la eficiencia industrial. No obstante ello, modelos más generales e inclusión de nuevas variables en la ecuación de la ineficiencia son procedimientos necesarios para obtener estimaciones más robustas.
En términos de políticas públicas, los resultados ayudan a identificar áreas de actuación prioritaria: si el objetivo es promover la mejoría de la eficiencia técnica de las empresas, por ejemplo, el objeto de actuación gubernamental consistirá en aquellas unidades más ineficientes. Si además los recursos públicos para incentivar la industria son limitados, aquí se ha presentado un análisis detallado de los municipios en los cuales la industria funciona con menores niveles de eficiencia técnica. Este estudio contribuye, así, en la identificación de prioridades de atención a partir de una política industrial activa. Si el objetivo es aumentar el desempeño conjunto de las firmas, entonces la focalización estaría en las firmas más eficientes.
No es irrelevante señalar que aunque los resultados son limitados en función del período de análisis de este estudio, investigaciones adicionales, aquí revisadas, muestran que las tendencias por nosotros encontradas, en el sentido de la caída en los niveles de eficiencia industrial en México, son estructurales, por depender de variables también estructurales tales como la educación formal de los trabajadores, el grado de concentración industrial y los salarios. Así, desde el punto de vista de la eficiencia industrial, acciones simultáneas tendrían que ser emprendidas desde una política industrial activa para lograr aumentar la productividad conjunta de la industria nacional: incentivos salariales, inversión pública en programas de reemplazo de maquinaria y equipo, así como programas más eficientes de capacitación al trabajo permitirían incentivar aumentos de productividad total de los factores.
Bibliografía
Albuquerque, E. M. (2000). Análise da performance produtiva e tecnológica dos clusters industriais na economia brasileira. Informe final, investigación integrante del proyecto BRA 97/013, Contrato No. 1999/005596, Brasilia. [ Links ]
Álvarez, I; Becerril, O; Del Moral y Vergara, R. (2008). "Aplicación del Data Envelopment Analysis a la delimitación de la frontera tecnológica en México (1970–2003)". Enlaces: revista del CES Felipe II, Núm. 8, ISSN 1695–8543. [ Links ]
Banco de Mexico, Índice Nacional de Precios al Productor (2010); referencia electrónica: http://www.banxico.org.mx/PortalesEspecializados/inflacion/inflacion.html [ Links ]
Battese, G. E. y Coelli, T. J. (1995). «A model for technical inefficiency effects in a stochastic frontier production function for panel data», Empirical Economics, n. 20, pp. 325–332 [ Links ]
Becerril, O; Álvarez, I; Del Moral, L (2009). "Do infrastructures influence the convergence of efficiency in México?". Journal of Policy Modeling. Volume 32, Issue 1, Pp. 120–137. [ Links ]
Farrell, M. J. (1957). "The measurement of productive efficiency". Journal of the Royal Statistical Society, London, v. 120, pp. 253–281. [ Links ]
Fuentes H. J. y Armenta L. (2006). "Las políticas públicas y la productividad: del diagnóstico a la solución efectiva. El caso de San Mateo Atenco". Análisis Económico, Vol. XXI, N° 047, 281–306. Universidad Autónoma Metropolitana–Azcapotzalco. Mexico City, México. [ Links ]
Gagnepain, Philippe (2002). "Stochastic Frontiers and Asymmetric Information Models"; Journal of Productivity Analysis, 18. [ Links ]
Grasetti, Luca (2009). A mixture based stochastic frontier model Dept. of Statistical Sciences – University of Udine, Italy. [ Links ]
Greene, H. W. (2005). "Fixed and Random Effects in Stochastic Frontier Models", Journal of Productivity Analysis 23. [ Links ]
Hausman, J. A. (1978). "Specification tests in econometrics" Econometrica, London, v. 46, n. 6, pp 1251–1271. [ Links ]
Hjalmarsson, L., Kumbhakar, S. C. y Heshmati, A. (1996). "DEA, DFA and SFA: A Comparison", The Journal of Productivity Analysis, 7. [ Links ]
Jondrow, J., Lovell, C. A., Materov, I. y P. Schmidtt (1982). "On the estimation of technical inefficiency in the stochastic frontier production function model", Journal of Econometrics 19. [ Links ]
Kopsakangas–Savolainen Maria y Rauli Svento (2008). Observed and unobserved heterogeneity in stochastic frontier models; Department of Economics, University of Oulu, Working Paper No. 0805. [ Links ]
Kumbhakar, S. y Lovell, K. (2000). Stochastic frontier analysis, Cambridge: Cambridge University Press. [ Links ]
Kumbhakar y Hjalmarsson (1993). "Technical Efficiency and Technical Progress in Swedish Dairy Farms" In H. Fired, K. Lovell and S. Schmidt (eds). The Measurement of Productive Efficiency: Techniques and Applications. New York: Oxford University Press. [ Links ]
Lau, L. J., Jamison, D. T., Lius, S. y Rivkin, S. (1993). Education and economic growth: some cross–sectional evidence from Brazil. Journal of Development Economics, vol. 41, pp. 45–70. [ Links ]
Maddala, G. S. (1994). "A note on the form of the production function and productivity in measurement and interpretation of productivity". En: MADDALA, G. S. (Org.), Econometric Methods and Applications. London, Aldershot: Edward Elgar, v. 1, pp. 57–65. [ Links ]
Odeck, J. (2007). "Measuring technical efficiency and productivity growth: a comparison of SFA and DEA in Norwegian grain production data", Applied Economics, 39. [ Links ]
Oliveira Pires, Jorge y Fernando García (2004). Productivity of Nations: a Stochastic Frontier Approach to Tfp Decomposition; Textos para discussao from Escola de Economia de Sao Paulo, Getulio Vargas Foundation (Brazil). [ Links ]
Pitt, M., y L. Lee (1981). "The Measurement and Sources of Technical Inefficiency in Indonesian Weaving Industry", Journal of Development Economics, 9. [ Links ]
Schmidt, P.; Sickles, R. (1984). "Production frontiers and panel data", Journal of Business & Economics Statistics, v. 2, n.4. [ Links ]
2 Datos de panel son combinaciones de datos de corte transversal con datos de series de tiempo. Como es discutido en Schmidt & Sickles (1984), en particular, tres grandes dificultades pueden ser resueltas cuando se utiliza un panel de datos: i) La eficiencia técnica de una firma particular puede ser estimada consistentemente cuanto T  ∞: agregar más observaciones a una misma firma genera informaciones que no se obtendrían con el incremento de más firmas a la muestra; ii) hipótesis restrictivas sobre la distribución de los errores –necesarias en un análisis de cross–section– pueden ser evitadas con el uso de un panel de datos; iii) finalmente, estimaciones de los parámetros de la frontera y de la (in)eficiencia de las firmas pueden ser obtenidas sin suponer que la ineficiencia no sea correlacionada con los regresores.
∞: agregar más observaciones a una misma firma genera informaciones que no se obtendrían con el incremento de más firmas a la muestra; ii) hipótesis restrictivas sobre la distribución de los errores –necesarias en un análisis de cross–section– pueden ser evitadas con el uso de un panel de datos; iii) finalmente, estimaciones de los parámetros de la frontera y de la (in)eficiencia de las firmas pueden ser obtenidas sin suponer que la ineficiencia no sea correlacionada con los regresores.
3 Las variables Y, X, K, L, V, U, escritas con letras minúsculas, representan el logaritmo del valor original. Así: yu = log(Yit); xit = log(Xit);kit = log(Kit);1it= log(Lit);vit = log(Vit) y uit = log(Uit).
4 El software utilizado es el Frontier 4.1 (desarrollado por Battese y Coelli, 1995), por medio del cual son obtenidas las estimaciones de los parámetros de la función de producción de frontera estocástica simultáneamente a los parámetros de la ecuación de la ineficiencia.
5 Maddala (1994) observa que medidas de cambio tecnológico y de eficiencia son insensibles a la elección de la forma funcional de producción porque ambas propiedades están relacionadas a desplazamientos de la isocuanta y no a su forma funcional.
6 Cálculo del cuociente de ubicación: (EMPsectori/EMPmunicipioi) / (total del país (EMPsector/total del país EMP), ponderado por porcentaje de empleo
7 Los valores son deflactados por el Índice Nacional de Precios al Productor a precios constantes de 2008. Banco de México, Índice Nacional de Precios al Productor 2010; referencia electrónica: http://www.banxico.org.mx/PortalesEspecializados/inflacion/inflacion.html
8 Ver, por ejemplo, Lau et al (1993).
9 El objetivo aquí no es agotar todas las explicaciones posibles de las diferencias de eficiencia de las firmas, sino analizar la importancia de las variables que se pueden medir más rápida y directamente.
10 El estadístico razón de verosimilitud (Prueba LR) λ =–2{log[likelihood(H0)]–log[likelihood(H1)]} tiene, aproximadamente, una distribución chi–cuadrada (Xk2) con parámetro k = n0 de parámetros asumidos como cero en la hipótesis nula, dado que H0 es verdadera.














