Suplemento

 

Ajuste recursivo con transformaciones invariantes y bootstrapping: El caso de una caminata aleatoria con intercepto

 

Eddy Lizarazu Alanez^* y José A. Villaseñor Alva^**1

 

^* (UAM–Iztapalapa), eddy.lizarazu@yahoo.com.

^** Instituto de Socioeconómicas, Estadística e Informática (ISEI), Campus Montecillo, Colegio de Postgraduados, jvillasr@colpos.mx.

 

Fecha de recepción: 22/05/2009
Aceptación: 29/08/2010

 

Resumen

Usamos simulaciones de Monte Cario para estudiar el desempeño de la prueba de raíz unitaria de Shin–So (DFSS) bajo los enfoques de transformaciones invariantes y el bootstrapping. Si la hipótesis alternativa es un proceso estacionario alrededor de una tendencia lineal, entonces la prueba bootstrap paramétrica es la mejor en términos de la potencia estadística. Sin embargo, si transformamos las observaciones para construir una prueba invariante, entonces la prueba DFSS es la mejor. Por consiguiente, la recomendación es usar transformaciones invariantes de la prueba de raíz unitaria de Shin–So debido a que su ejecución es directa y de menor coste.

Palabras clave: Ajuste de tendencia recursivo, estadístico DF, método bootstrap parámetrico.

Clasificación JEL: C12, C15, C32

 

Abstract

We use Monte Carlo simulations to study the performance of Shin–So unit root test (DFSS) under invariant transformation approaches and bootstrapping. If the alternative hypothesis is a stationary process around a linear trend, then the parametric bootstrap test is the best in terms of statistical power. However, if we transform the observations to build an invariant test, then the DFSS test is the best. Therefore, the recommendation is to use transformations of the invariant Shin–So unit root test because its implementation is straightforward and less costly.

 

Introducción

La prueba de Dickey–Fuller (DF) sirve para probar si una serie proviene de un proceso estocástico raíz unitaria. El desempeño de la prueba depende de supuestos sobre la especificación de la hipótesis nula. Estos supuestos son: 1) la presencia de un intercepto en la caminata aleatoria, 2) la distribución de probabilidad del término de error y 3) la condición inicial del proceso estocástico. El estadístico DF experimenta problemas en la potencia y tamaño de la prueba. La potencia baja se manifiesta sobre todo cuando el proceso es cuasi–raíz unitaria (débilmente estacionario), mientras que la distorsión en el tamaño de la prueba surge debido a cambios estructurales en la hipótesis nula. Hay progresos en torno a la metodología Dickey–Fuller, los cuales incluyen regresiones forward–reverse, estimadores simétricos ponderados y variables instrumentales, así como estadísticos específicos, por ejemplo, las pruebas Kwiatkowki–Phillips–Schmith–Shin, Leybourne–McCabe, Phillps–Perron y otras más.

El método de ajuste recursivo propuesto por Shin–So (2001, 2002) y So–Shin (1999) reduce el sesgo en la estimación de la ecuación autorregresiva, con lo que mejora la potencia de la prueba DF. Dada la reducción del sesgo, Cook (2002, 2003), Kim, et al. (2002, 2004) y Leybourne, et al. (1998, 2000) proporcionan evidencia de robustez de la prueba Shin–So (DFSS) cuando la caminata aleatoria es pura y experimenta cambios estructurales en su media. Por su parte, Lizarazu–Villaseñor (2007) muestran la robustez de la prueba DFSS a la coexistencia de rompimientos en la media y la varianza del proceso estocástico.

La prueba DFSS para una caminata aleatoria pura no representa dificultades. No es el caso si la caminata aleatoria tiene una deriva, ya que la distribución de probabilidad del estadístico DFSS es compleja (o bien, desconocida). La dificultad de aplicar la prueba de Shin–So, sin embargo, se evita al implementar las siguientes acciones: 1) Usar transformaciones para construir una prueba invariante a los parámetros bajo la hipótesis nula y 2) emplear la técnica boostrap paramétrica, cuya ventaja es la estimación del intercepto de la caminata aleatoria. Esta cuestión es precisamente el meollo del problema de una prueba no–invariante al intercepto de la caminata aleatoria, puesto que es necesario calcular los cuantiles de la distribución del estadístico.

En este artículo evaluamos el desempeño de estos dos enfoques mediante simulaciones de Monte Cario. Los problemas asociados a la prueba de raíz unitaria DF son vastos, por lo que es importante señalar que nuestro análisis concierne a la metodología de Bhargava (1986). La práctica de la prueba de raíz unitaria se exterioriza mediante la ecuación de estimación de los parámetros. La metodología Dickey–Fuller (1979, 1981) implica estimar la ecuación y_t = α + (βt + ρy_t–1 + u_t, donde . Por lo tanto, la implementación de la técnica bootstrap será distinta dependiendo de la metodología Dickey–Fuller o Bhargava.

El procedimiento de anidamiento de las hipótesis en el enfoque Barghava conlleva una estimación secuencial de los parámetros. Previamente es necesario estimar α y β a partir de la regresión de la ecuación y_t = α + (β + v_t, y después hay que estimar Φ mediante la ecuación v_t = Φv_t–1 + ε_t, donde 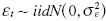. Las ecuaciones de Bhargava implican: y_t = α (1–Φ) + Φy_t–1 + ε_t, por lo que si H₀ : Φ = 1 entonces el proceso es una caminata aleatoria con intercepto, y si , el proceso es estacionario alrededor de una tendencia lineal. En ambas metodologías se tiene la misma hipótesis nula, pero en la metodología Dickey–Fuller la ecuación a estimar es ex professo. Por tal motivo, el alcance de los resultados depende no sólo del proceso generador de los datos simulados, sino sobre todo de la ecuación utilizada en la estimación de los parámetros.

Si bien no es un caso general, el estudio de este artículo es un avance en tal dirección. Es decir, es conveniente examinar casos particulares y después ir a casos más generales. Por lo tanto, en este tenor, el artículo está organizado de la siguiente manera: en la segunda sección se presentan algunas cuestiones teóricas de la prueba DFSS para el caso de una caminata aleatoria pura. En la tercera sección se muestran las dificultades teóricas de la prueba DFSS en el caso de una caminata aleatoria con intercepto. En la cuarta sección se explica en qué consiste una prueba estadística invariante al parámetro de la hipótesis nula. En la quinta sección se explica el método bootstrap paramétrico. En la sexta sección se analizan los resultados de las simulaciones de Monte Cario. Por último, en la séptima sección, incluimos algunos comentarios de conclusión.

 

La prueba DF de Shin–So para una caminata aleatoria pura

Consideremos el horizonte de tiempo t = 1,..., T en las siguientes especificaciones.

Donde ε_t~ iid(0,σ²). La estructura anterior de ecuaciones da lugar a un proceso estacionario, donde el parámetro α es la media de y_t, mientras que 0 < Φ < 1 es el coeficiente de la ecuación autorregresiva de las desviaciones de y, en relación a α.² Lo anterior es evidente, pues al insertar [2] en [1] se arriba a la siguiente ecuación:

Alternativamente:

Si la hipótesis nula es H₀ : Φ = 1 entonces la ecuación [4] se convierte en una caminata aleatoria pura: y_t = y_t_₁ + ε_t.

La prueba de Dickey–Fuller (DF) se basa en el siguiente estadístico 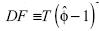. Se rechaza la hipótesis nula cuando el estadístico es menor a la constante crítica asociada al nivel de significancia. El estimador es obtenido por el método de mínimos cuadrados ordinarios (MCO).

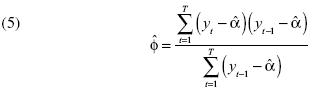
Bajo la hipótesis nula, el estadístico DF sigue una distribución teórica asintótica conocida como la distribución Dickey–Fuller, la cual es representada por la siguiente distribución de probabilidad:

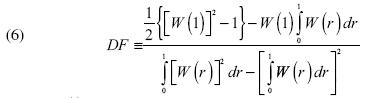
donde w (.) es un proceso de Weiner o Browniano.

El estimador 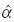es necesario en la construcción de , y el mismo es el resultado de una sucesión de cálculos. En primer lugar, se estima el parámetro a de la ecuación [1] mediante MCO, lo que da lugar a:

En seguida se extrae el valor de 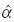de las observaciones de y_t para construir (véase la ecuación [5]).

En la regresión de la ecuación [4] está latente un problema correlación del regresor 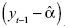y el término de error ε_t. La siguiente fórmula proporciona una idea de la magnitud de la correlación inmersa.

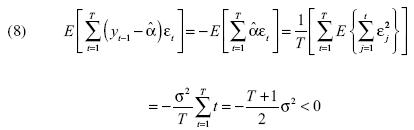
El problema desaparece si utiliza otro estimador para a. Siguiendo a Shin–So (2001, 2002) y So–Shin (1999), el estimador que elimina el sesgo viene definido por la siguiente ecuación:

Éste es conocido como el '"estimador de ajuste recursivo" debido a que la media muestral se calcula secuencialmente para los distintos períodos y tamaños de muestras concebidas desde t hasta las T observaciones.

Al utilizarse en la extracción de la media estimada de las observaciones de y_t, desaparece la correlación, por lo que el estimador de ajuste recursivo de Φ viene a ser:

El estadístico 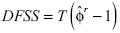sigue una distribución teórica no estándar conocida como la distribución Dickey–Fuller–Shin–So, la cual es representada por la siguiente expresión:

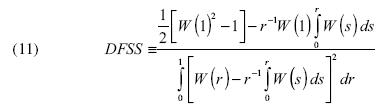
donde r ε (0, 1) y W (.) es un proceso de Weiner o Browniano. En este caso, también se rechaza la hipótesis nula si el estadístico DFSS es menor a la constante crítica del cuantil apropiado.

La ecuación [11] es diferente de [6] y siguiendo a Shin–So (2001, 2002), la potencia de la prueba DFSS es mejor en relación con la prueba DF, donde la hipótesis alternativa es estacionariedad. La

explicación no sólo descansa en la propiedad, sino también en la reducción del sesgo de estimación de 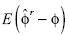al utilizar el estimador 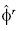, lo que lleva consigo valores críticos de más cargados a la derecha que los correspondientes a 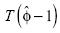. Por lo tanto, la tasa de aceptación de H₁ en el caso de valores 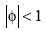será forzosamente mayor en la prueba DFSS.

 

La prueba DF de Shin–So para una caminata aleatoria con intercepto

Consideremos el tiempo t = 1, ..., T en el siguiente conjunto de ecuaciones:

La primera ecuación incluye a la constante α y a la tendencia lineal β (coeficiente del tiempo) más una variable aleatoria v _t. La segunda ecuación es una ecuación autorregresiva de primer orden de la variable aleatoria v _t, donde se incluye un término de error ruido blanco denotado por ε_t ~ iid(0,σ²).

Si la hipótesis nula es H₀ : Φ = 1, entonces de las ecuaciones [12] y [13] implican una caminata aleatoria con intercepto deriva:

La ecuación anterior también se puede expresar en términos de su primera diferencia:

En tal caso, Δy_t no depende de α, pero sí del valor de β. La presencia de este parámetro desempeña un papel importante en la construcción de una prueba estadística, tal como se muestra más adelante.

La hipótesis alternativa H₁ : 0 Φ< 1 corresponde a un proceso estocástico estacionario alrededor de una tendencia lineal:

donde son las observaciones después de descontar la componente determinista.

En este caso, la construcción del estadístico de la prueba DF exige la estimación de los parámetros de la ecuación [12], la cual puede reescribirse como:

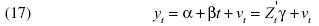
donde

El estimador MCO de y se calcula de la siguiente manera:

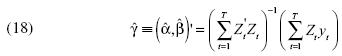
En la prueba el estimador es:

donde .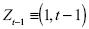

En analogía a la sección anterior, la prueba DF exhibe una potencia mayor si la componente determinista de [12] se estima secuencialmente para cada posible muestra de tamaño d ε (2,T). En tal caso, el estadístico de ajuste recursivo es 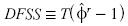, donde Tes el tamaño de la muestra y 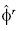es el estimador de ajuste recursivo.

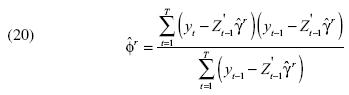
donde 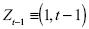. El estimador 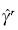es igual a:

donde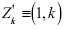

La regla de rechazo de la hipótesis nula de ambas pruebas es que los estadísticos de prueba DF y DFSS sean respectivamente menores a las constantes críticas pertinentes. Sin embargo, es imposible calcular las constantes críticas, ya que se desconocen las distribuciones de probabilidad de ambos estadísticos.

Además, otro inconveniente es que la componente determinista conlleva la presencia de β. ¿Por qué? Consideremos las transformaciones para los períodos t y t –1:

donde 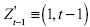. El estimador es equivalente a [21] con la salvedad de que el índice del operador sumatoria llega a t –1.

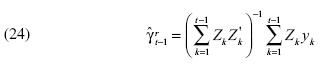
Se puede mostrar que los estimadores de ajuste recursivo dan lugar a la siguiente expresión:

Al premultiplicar y se tiene:

De esta manera, se llevan a cabo las siguientes operaciones:

Si las transformaciones involucradas toman en cuenta la condición inicial y₀ = 0 del proceso estocastico, entonces la iteración hacia atrás de la ecuación [14] para los períodos t y k implica:

donde 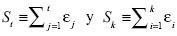. De esta manera, transformaciones [27] y [28] dan lugar a las siguientes ecuaciones:

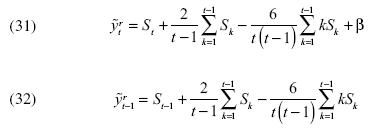
donde 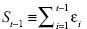. Es evidente que tant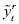o como 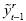son una función de las sumas S_i (i = k,t,t–1). Además, si bien 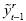no depende del parámetro β, no sucede lo mismo con 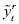. En efecto, la primera diferencia de y_t, es igual al parámetro β más la variable aleatoria ruido blanco:

Por consiguiente, la prueba DFSS no es invariante al parámetro de tendencia β.³ La existencia de este problema exige una solución. Al respecto, existen dos posibles enfoques: el primero consiste en transformaciones adecuadas de las observaciones. El segundo enfoque es incorporar estimaciones del parámetro β con el método bootstrap paramétrico. En este último caso se cuantifican los cuantiles de la distribución de probabilidad del estadístico. En la sección siguiente abordamos el enfoque de las transformaciones invariantes y dejamos para la sección subsiguiente el boostrap.

 

Transformaciones invariantes de las variables

En relación con el ajuste recursivo existen al menos tres alternativas de transformaciones para construir una prueba invariante al parámetro β. La primera es la transformación de Taylor (2002), la cual consiste en descontar la componente determinista estimada de los períodos t y t–1. La segunda transformación se debe a Chang (2002), la cual esencialmente consiste en incorporar a la construcción de la prueba invariante el estimador del parámetro de estorbo. Por último, la tercera transformación es un artificio ad–hoc de eliminación algebraica del parámetro β.

 

La Transformación de Taylor

Según las ecuaciones [31] y [32], la primera diferencia de la variable aleatoria 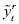depende del parámetro β, por lo cual es natural proceder con los estimadores 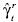y para transformar respectivamente a las variables y_ty y_t_₁. En tal caso, la ecuación [22] permanece intacta y sólo se afecta [23], la cual se sustituye por:

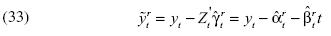
donde 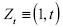. El cálculo de 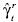se realiza de la siguiente manera:

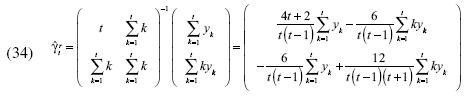
La modificación de Taylor es la transformación ideal y las variables serán calculadas de la siguiente manera:

En seguida se muestra que estas transformaciones son independientes del parámetro de estorbo β. En efecto, al iterar hacia atrás y apoyados en ciertos supuestos particulares se llega a las siguientes ecuaciones:⁴

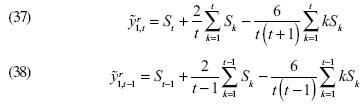
Por lo tanto, la primera diferencia de 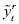, es un proceso estocástico independiente del parámetro .

 

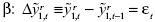La Transformación de Chang

El estimador MCO de β bajo la ecuación [14], es decir, la hipótesis nula, es igual a:

El estimador MCO de β se incorpora en la ecuación [23] con signo negativo. De esta manera, la transformación buscada es igual a:

De la ecuación [40] no es difícil arribar a la siguiente ecuación:

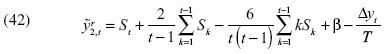
Si bien, en muestreo repetido tenemos 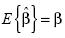lo que interesa crucialmente es darse cuenta que , por lo que la transformación implica:

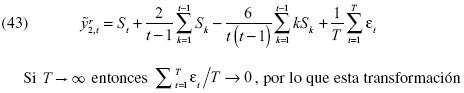
da lugar a un estadístico independiente del parámetro β.

 

La transformación ad–hoc

Supongamos de nuevo la condición inicial del proceso estocástico y₀ = 0 , entonces bajo la hipótesis nula el proceso generador de datos es:

A partir de la ecuación [44], obsérvese que es igual a:

De esta manera, la transformación ideal es el resultado de las siguientes operaciones:

Cuando las ecuaciones anteriores son iteradas hacia atrás entonces obtenemos una prueba estadística independiente de β, ya que se cumplen las siguientes ecuaciones:

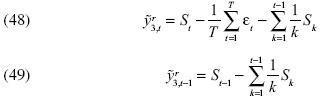
Por consiguiente, las tres clases de transformaciones se pueden utilizar para construir una prueba estadística invariante con la seguridad de que el valor del parámetro β no influirá en el tamaño y la potencia de la prueba.

 

El bootstrap paramétrico para la prueba de DFSS de Shin–So

El método bootstrap facilita el estudio de las propiedades de un estadístico cuando no se conoce su distribución teórica (finita y/o asintótica). Tal como en la inferencia paramétrica, la técnica bootstrap pretende describir los estados verdaderos de la naturaleza. La idea es generar una cantidad grande de muestras bootstrap con el propósito de calcular los constantes críticas del cuantil de la distribución de probabilidad del estadístico bootstrap. Cuando la distribución empírica del estadístico bootstrap es una buena aproximación de la distribución teórica del estadístico corriente, entonces la prueba bootstrap conduce a inferencias correctas.

La inferencia paramétrica procede en términos de (1) los errores estándares de los estimadores, (2) los intervalos de confianza de los estimadores de los parámetros desconocidos y (3) los valores p del estadístico de prueba. Supongamos un conjunto de distribuciones P, donde P₀ es una distribución particular, entonces (l)–(3) se cuantifican a través de funcionales del tipo Q(p₀), donde 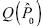es la estimación bootstrap y 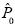es el estimador bootstrap de P₀. Si P₀ se indexa mediante el parámetro θ, entonces el bootstrap se dice que es paramétrico y es denominado bootstrap parámetrico. En estos casos, el proceso generador de datos bootstrap está caracterizado por el parámetro estimado.

En algunas situaciones es imposible hallar el proceso generador de datos bootstrap, por lo que el estadístico bootstrap no tendrá la misma distribución del estadístico corriente. Si el estadístico no es pivotal,⁵ es deseable obtener una buena estimación del proceso generador de datos verdadero. Por tal motivo, el bootstrap paramétrico exige tanto como sea posible la estimación de los parámetros desconocidos del proceso generador de datos verdadero. La razón es que estas estimaciones son utilizadas en la construcción del proceso generador de datos bootstrap, así como en las muestras bootstrap.

La distribución de probabilidad del estadístico DFSS se basa en el proceso generador de datos de la hipótesis nula. Diversos valores de a y P satisfacen las ecuaciones [12] y [13] incluso si Φ = 1. Sin embargo, el parámetro a no aparece en el proceso generador de datos de la hipótesis nula. Por ende, en la generación de las muestras corrientes interesa sólo la estimación del parámetro β el que debe ser estimado consistentemente para que sea posible construir las muestras bootstrap y computar el estadístico bootstrap.

El método bootstrap en el caso de la prueba DFSS se lleva a cabo a términos de las siguientes etapas:

Se generan muestras para un valor fijo de β bajo el proceso generador de datos de la hipótesis nula. Por supuesto, el valor del parámetro β se fija previamente y de forma arbitraria.

Se estima consistentemente el parámetro β mediante el ajuste recursivo de Shin–So y se construyen 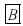muestras bootstrap bajo el proceso generador de datos de la hipótesis nula.

En cada muestra bootstrap se calcula el estadístico DFSS y dadas las repeticiones entonces se calcula la distribución empírica del estadístico bootstrap.

Se elige un cuantil apropiado de la distribución empírica (asociado al error tipo I) del estadístico bootstrap con el que se realiza la prueba de raíz unitaria bajo la misma regla de rechazo de la hipótesis nula del estadístico corriente.

Por último es necesario señalar dos cuestiones. La primera es recalcar que no interesa el valor del parámetro a cuando se construye la muestra bootstrap debido a que este parámetro se elimina para cualquier período t = 1,...,T del proceso generador de datos bajo la hipótesis nula.⁶ La segunda cuestión es que el procedimiento (l)–(4) permite calcular no sólo el tamaño de la prueba DFSS, sino también la potencia de la prueba. En cualquier caso se utilizan los cuantiles de la distribución empírica del estadístico bootstrap.

 

Simulaciones Monte Cario con la prueba DFSS de Shin–So

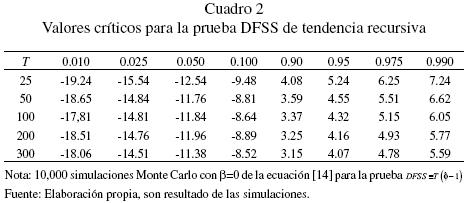
El primer análisis concierne a la prueba DFSS de tendencia recursiva, cuyos valores críticos se reportan en el cuadro 2 con los resultados para 10,000 replicaciones Monte Cario. Los datos fueron generados en R para números aleatorios de la distribución normal estándar de acuerdo a la ecuación [14] y diferentes valores de β y distintos tamaños de muestra T. Por supuesto, los valores críticos de muestra finita corresponden a β = 0 con Φ = 1. La componente de tendencia lineal es estimada por mínimos cuadrados ordinarios recursivos. El análisis de la prueba DFSS procede en los términos de los datos transformados como se indican las ecuaciones [22] y [23], los cuales dependen del parámetro β.

Del análisis del cuadro 1, nuestra conclusión es que valores del parámetro β más grandes pero positivos están asociados con un error tipo I más grande. El problema persiste cuando aumenta el tamaño de la muestra; por ende, el parámetro β influye en la prueba DFSS porque distorsiona el tamaño de la prueba. Dicho de otra manera, la distribución de probabilidad del estadístico DFSS es sensible a la presencia de β, lo que significa que no es adecuada para llevar a cabo la prueba de raíz unitaria para una caminata aleatoria con intercepto debido a que a tiende a rechazar la hipótesis nula más de lo previsto.

 

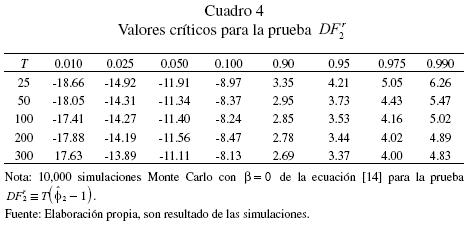
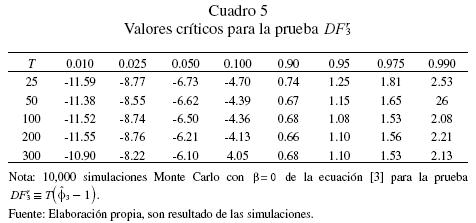
¿Qué pasa si realizamos la prueba DFSS con las transformaciones invariantes? Los valores críticos para estas pruebas se reportan en los cuadros 3, 4 y 5. Los estadísticos de prueba asociados a los distintos tipos de transformaciones son denotados por 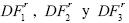, respectivamente. En el cuadro 6 se presentan los resultados en relación con el tamaño y la potencia de la prueba de raíz unitaria. A este respecto se debe indicar que estos resultados corresponden a datos generados bajo la hipótesis nula en el caso de una caminata aleatoria pura. Las transformaciones invariantes funcionan relativamente bien y, como es de esperar, el tamaño de la prueba se preserva para todos los estadísticos de prueba. En particular, el estadístico 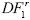prácticamente resulta ser el mejor estadístico en relación a la potencia estadística. Si bien la potencia es relativamente alta sobre todo para tamaños de muestra T ≥ 200, empero, en el caso de muestras pequeñas T ≤ 50, la potencia de todos los estadísticos es demasiado baja. Algo similar se encuentra cuando el proceso estocástico es débilmente estacionario 0.95 < (β < 1 y el tamaño de muestra es T < 100.

Los resultados no son diferentes cuando los datos se generan bajo la hipótesis nula para un valor de β diferente de cero. De hecho, las simulaciones muestran resultados prácticamente idénticos en relación con la potencia estadística. En este caso, los valores críticos a un 5% de nivel de significancia se reportan en el cuadro 7. Los datos generados para la distribución normal estándar de una caminata aleatoria con intercepto incluyen valores de . Evidentemente persiste la dependencia de la prueba DFSS a este parámetro pues, a medida que su valor crece, los valores críticos decrecen independientemente del tamaño de la muestra.

Ahora bien, el problema con la prueba bootstrap DFB es que las simulaciones demandan un costo de tiempo elevado, especialmente si el tamaño de muestra es mayor a 100 datos. Por tal motivo, el estudio de simulación se realiza para muestras de tamaño 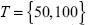y un valor específico de β = 1. Consecuentemente se contemplan 999 muestras bootstrap y 1000 réplicas para cada una de ellas. El tamaño y la potencia de todas las pruebas se reportan en el cuadro 8, incluyendo al estadístico DFSS, el cual sabemos tiene el inconveniente de depender del valor de β. En tal situación, la prueba DFB toma en cuenta la estimación del parámetro β y considera dicha estimación para calcular las constantes críticas de los cuantiles de la distribución empírica del estadístico bootstrap.

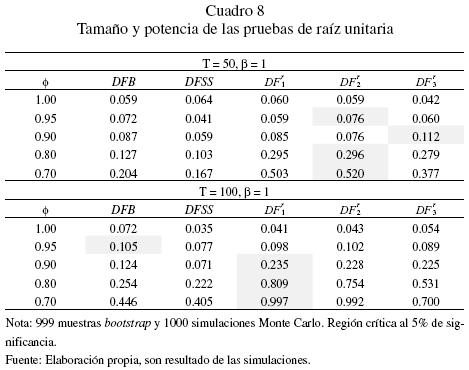
Dado que el interés es averiguar sobre las ventajas de la técnica bootstrap se tienen las siguientes consideraciones:

La prueba DFB es la mejor en potencia respecto a la prueba DFSS con independencia del tamaño de la muestra.

Hay una ligera distorsión en el tamaño de la prueba de todos los estadísticos cuando el tamaño de la muestra es relativamente pequeña (T = 25). El problema desaparece cuando el número de datos de la muestra es grande, excepto en el caso de la prueba DFB.

Cuando el tamaño de la muestra es mediano (T = 50), el estadístico de prueba 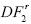de Chang es la mejor en términos de su potencia, pero cuando el tamaño de la muestra aumenta (T= 100), la prueba 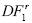es la mejor respecto a la hipótesis de estacionariedad. Esto ratifica y confirma los resultados de la simulación para β igual a cero.

En el rango 0.8 < Φ < 1, la potencia de todas las pruebas es baja, no obstante en el caso de 0 < Φ ≤ 0.7 , la prueba 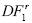es la de mejor potencia especialmente cuando el tamaño de la muestra es T= 100.

Por último, es necesario indicar dos cuestiones. En primer lugar, en relación con el punto (d), como indican Madala–Kim (1998), todas las pruebas de raíz unitaria de la clase univariada experimentan una potencia baja para los procesos estacionarios cercanos a una raíz unitaria. Por lo tanto, los resultados de las simulaciones encajan bien con la evidencia reportada por otras investigaciones. En segundo lugar, tocante al punto (c), si bien la prueba DFB no es mejor que las pruebas 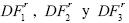, es ilustrador saber que el método boostrap puede mejorar la potencia de la prueba de raíz unitaria DFSS cuando la hipótesis nula es una caminata aleatoria con intercepto. No obstante, es recomendable utilizar cualquiera de las pruebas con transformación invariantes.

 

Conclusiones

Muchas series históricas se parecen a una caminata aleatoria con intercepto. Nelson–Plosser (1982) dan evidencia de que la mayoría de las variables macroeconómicas básicas como el PIB, el nivel de precios y otras más tienen raíces unitarias. En muchos estudios se corrobora dicho resultado y, sin embargo, no se cuestiona si la prueba arroja una conclusión sistemáticamente diferente. Es imperioso percibir que el ajuste de la tendencia lineal por mínimos cuadrados ordinarios induce a un sesgo en la estimación del coeficiente de la ecuación autorregresiva de la variable estudiada debido a la correlación del regresor con el término de error.

Shin–So (2001, 2002) y So–Shin (1999) remedian el sesgo al construir el estadístico DFSS con base en la estimación recursiva de la componente determinista, pero la prueba no se puede implementar en el caso de una caminata aleatoria con una deriva. ¿Por qué? La distribución de probabilidad del estadístico se puede obtener por métodos conocidos y la distribución asintotica del estadístico tiene validez estrictamente si el tamaño de la muestra es "grande". En otros casos, la distribución de probabilidad del estadístico depende de supuestos fuertes o bien su construcción es complicada. Éste es el caso de la prueba DFSS de Shin–So. ¿Qué se puede hacer entonces si no puede implantar al caso de una caminata aleatoria con derival Se debe proceder en términos de las transformaciones al parámetro de tendencia lineal o bien bajo la técnica del bootstrap parámetrica. ¿Cuál es el mejor procedimiento? Cuando la hipótesis alternativa es un proceso estacionario alrededor de una tendencia lineal y se trabaja con las observaciones originales, la evidencia está del lado del bootstrap paramétrico, es el mejor en términos de la potencia estadística. Sin embargo, si los datos se transforman apropiadamente, entonces la prueba DFSS invariante de ajuste recursivo es la mejor. Por lo tanto, la recomendación es utilizar transformaciones invariantes de las observaciones debido a que su ejecución es directa y de menor coste.

En el futuro será necesario valorar el papel del parámetro de la caminata aleatoria en relación con la distorsión del tamaño de la prueba. La prueba DFSS no necesariamente es robusta, por ejemplo, a la presencia de "puntos de quiebre" examinadas por Perron (1989). Dicho de otra manera, cuando el valor del parámetro de tendencia cambia a lo largo del tiempo, la tasa de rechazo de la hipótesis nula podría aumentar, aun cuando el verdadero proceso es una caminata aleatoria, por lo que tendríamos un fenómeno "inverso de Perron" (Leybourne 1998, 2000). La prueba de bootstrap por construcción es robusta a rompimientos de los parámetros bajo la hipótesis nula, tal como lo sugiere el diseño de simulación Monte Carlo. Sin embargo, se desconoce si tal propiedad es una característica recurrente de la prueba DFSS invariante por lo que ésta es una tarea para una investigación futura.

 

Bibliografía

Bhargava, A. (1986). "On the Theory of Testing for Unit Roots in Observed Time Series". Review of Economic Studies, 53(3): 369–384.         [ Links ]

Chang, Y. (2002). "Nonlinear IV Unit Root Tests in Panels with Cross–sectional Dependency". Journal of Econometrics, 110(2):261–292.         [ Links ]

Cook, S. (2002). "Correcting Size Distortion of the Dickey–Fuller Test via Recursive Mean Adjustment". Statistics and Probability Letters, 60(l):75–79.         [ Links ]

Cook, S. (2003). "Size and Power Properties of Powerful Unit Root Tests in the Presence of Variance Breaks". PhysicaA: Statistical Mechanics and its Applications, 317(3–4):432–448.         [ Links ]

Dickey, D. A. y Fuller, W. A. (1979). "Distribution of the Estimators for Autoregressive Time Series with a Unit Root". Journal of the American Statistical Association, 74(366):427–431.         [ Links ]

––––––––––(1981). "Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root". Econometrica, 49(4): 1057–1072.         [ Links ]

Kim, T. H., Leybourne, S. y Newbold, P. (2002). "Unit Root Test with a Break in Innovation Variance". Journal of Econometrics, 109(2):365–387.         [ Links ]

Kim, T. H., Leybourne, S. y Newbold, P. (2004). "Behavior of Dickey–Fuller Unit Root Tests Under Trend Misspecification". Journal of Time Series Analysis, 25(5):755–764.         [ Links ]

Leybourne, S. y Newbold, P. (2000). "Behavior of the Standard and Symmetric Dickey–Fuller Type Tests When There Is a Break under the Null Hypothesis". Econometrics Journal, 3(1): 1–15.         [ Links ]

Lizarazu, E. y Villaseñor, J., (2007). "Efectos de Rompimientos bajo la Hipótesis Nula de la Prueba Dickey–Fuller para Raíz Unitaria". Agrociencia, 41:2, pp. 193–203.         [ Links ]

Leyborune, S., Milis, T. y Newbold, P. (1998). "Spurious Rejections by Dickey–Fuller Test in the Presence of a Break under the Null". Journal of Econometrics, 87(l):191–203.         [ Links ]

MacKinnon, J. G. (2006). "Bootstrap Methods in Econometric". Economic Record, 82(S1):S2–S18.         [ Links ]

Maddala, G. S. y Kim, In–Moo (1998). Unit Roots, Cointegration and Sructural Change. Cambridge: Cambridge University Press.         [ Links ]

Nelson, Ch. y Plosser, Ch., (1982). "Trends and Random Walks in Macroeconomic Time Series". Journal of Monetary Economics, 10(2):139–162.         [ Links ]

Perron, P. (1989). "The Great Crash, the Oil Price Shock, and the Unit Root Hypothesis". Econometrica, 57(6): 1361–1401.         [ Links ]

Rodrigues, P. (2006). "Properties of Recursive Trend–Adjusted Unit Root Tests". Economics Letters, 91(3): 413–419.         [ Links ]

Shin, D. W. y So, B. S. (2001). "Recursive Mean Adjustment for Unit Root Tests". Journal of Time Series Analysis, 22(5):595–612.         [ Links ]

Shin, D. W. y So, B. S. (2002). "Recursive Mean Adjustment and Test for Nonstationarities". Economics Letters, 75(2):203–208.         [ Links ]

So, B. S. y Shin, D. W. (1999). "Recursive Mean Adjustment in Time–Series Inferences". Statistics and Probability Letters, 43(l):65–73.         [ Links ]

Taylor, A. (2002). "Regression–based Unit Root tests with Recursive Mean Adjustment for Seasonal and Nonseasonal Time Series". Journal of Business and Economic Statistics, 20(2):269–281.         [ Links ]

 

Notas

¹ Agradecemos los comentarios de los dictaminadores anónimos. Asumimos la responsabilidad de los errores que pudieran persistir.

² La estructura de ecuaciones [3] y [4] es conocida como la metodología Bhargava, la cual es diferente a la metodología Dickey–Fuller. Véase Maddala–Kim (1998, pp. 37–39).

³ Rodrigues (2006) señala que la presencia del parámetro β en es un estorbo para el tamaño de la prueba. Este mismo autor reporta resultados de un estudio de simulación Monte Cario, según la cual, la potencia de la prueba estadística es sensiblemente deficiente para la hipótesis alternativa 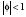con valores de Φ cercanos a la unidad. Sin embargo, el estudio de Rodrigues no explica si existen otras alternativas de resolución del problema.

⁴ Estos supuestos específicos son la condición inicial del proceso estocastico y la validez de la hipótesis nula.

⁵ De acuerdo con MacKinnon (2006), se dice que un estadístico es pivotal para la hipótesis nula si y sólo si para cada tamaño de muestra, la distribución del estadístico de prueba es la misma para todos los procesos de datos que satisfacen la hipótesis nula.

⁶ Además, cuando t = 0, la condición inicial del proceso es que y₀ = 0, lo que implica que v₀ = 0 y α sea cero.