Suplemento especial: Primer Seminario Internacional en Teoría Económica Contemporánea
Mesa 2: Finanzas y desarrollo

 

Un modelo estocástico de equilibrio general para valuar derivados y bonos

 

Francisco Venegas–Martínez¹

 

¹ Escuela Superior de Economía, Instituto Politécnico Nacional. Correo electrónico: fvenegas1111@yahoo.com.mx

 

Resumen

En este trabajo se desarrolla un modelo de equilibrio general en una economía con agentes idénticos. Estos agentes son racionales y toman decisiones de portafolio y consumo. Bajo los supuestos de que existe una acción cuyo precio es conducido por un movimiento geométrico Browniano y la tecnología es guiada por un proceso estacionario Markoviano con reversión a la media, se determinan en el equilibrio los precios de un derivado sobre la acción y un bono cupón cero.

Palabras clave: Equilibrio general, Consumidor racional, Derivados, Bonos cupón cero.

Clasificación JEL: D50, D91, G11.

 

Abstract

This paper is aimed at developing a general equilibrium model in an economy populated by identical agents. These agents are rational and make decisions on portfolio and consumption. Under the assumptions that exists a share whose price is driven by a geometric Brownian motion and the technology is guided by a stationary Markovian process with mean reversion, the prices of a derivative on a share and a zero coupon bond are obtained in the equilibrium.

 

Introducción

En los últimos años, la economía mundial, en su proceso de integración financiera, ha experimentado una serie de cambios y transformaciones profundas que han impactado tanto la forma de llevar a cabo el análisis económico, como el diseño mismo de la política económica. Estos cambios han abierto nuevos paradigmas que resaltan la exposición de los agentes a diferentes tipos de riesgos financieros.

Mucho se ha aprendido en los últimos años sobre los productos derivados financieros, sobre todo de los que tienen como subyacentes créditos hipotecarios o divisas, pero mucho queda todavía por aprender sobre sus efectos en las economías en los ámbitos local y global. Es importante destacar que los mercados de derivados no originaron la crisis de 2008, sólo la exacerbaron al generar una burbuja especulativa. Es también necesario aclarar que los derivados financieros no son armas de destrucción masiva ni instrumentos financieros tóxicos para las economías, simplemente, y como en todo mercado, hay perdedores y ganadores. La gran diferencia con otros mercados es la magnitud colosal de las apuestas.

La determinación de los precios de diferentes activos (subyacentes y derivados) ha sido un tema de gran relevancia en los últimos años; algunas investigaciones al respecto son, por ejemplo: Cox, Ingersoll y Ross (1985a), Grinols y Turnovsky (1993), Schmedders (1998) y Venegas–Martínez (2001), (2006) y (2006b), entre otros. Asimismo, se encuentran en la literatura diversos trabajos para valuar bonos; por ejemplo: Cox, Ingersoll y Ross (1985b), Longstaff (1989), Venegas–Martínez y González–Aréchiga (2002) y Lee y Li (2005).

En el presente trabajo se desarrolla un modelo de equilibrio general en una economía poblada por agentes idénticos que toman decisiones de consumo y portafolio. En la economía existen tres activos, en términos reales: acciones, contratos derivados sobre dichas acciones y un bono libre de riesgo de incumplimiento. Bajo el supuesto de que el precio del título accionario es conducido por un movimiento geométrico Browniano y la tecnología es guiada por un proceso Markoviano de difusión, se obtienen en el equilibrio los precios de un derivado sobre una acción y un bono cupón cero. La característica distintiva del modelo propuesto es que produce tasas con dinámicas alternativas a las encontradas en Cox, Ingersoll y Ross (1985b). Asimismo, esta investigación generaliza el modelo de Longstaff (1989).

 

Supuestos básicos de la economía

Considere una economía cerrada, la cual está poblada por individuos idénticos, maximizadores de utilidad. La economía produce y consume un solo bien de carácter perecedero. Los consumidores tienen acceso a una acción y un derivado sobre dicha acción. Los precios de estos activos están dados en términos reales.

 

Activos y sus precios

Suponga que el precio en términos reales, t, de la acción tiene una dinámica estocástica conducida por el movimiento geométrico Browniano de tal forma que

donde el parámetro de tendencia, µ_s , representa el rendimiento medio esperado, el parámetro de volatilidad, σ_s es la variación instantánea del rendimiento del activo y el proceso {U_t}_{t ≥ 0} es un proceso de Wiener definido sobre un espacio fijo de probabilidad ( Ω^U ,P^U). En lo que sigue, el precio del derivado de la acción se denotará por v_t = v (S_t ,t)

 

Restricción presupuestal del consumidor

La riqueza real, x_t , del individuo, en cada instante, está dada por:

Sea w_1t = S_t / x_t la proporción de la riqueza que el individuo asigna a la tenencia de acciones, w_2t = v_t / x_t la proporción de la riqueza que asigna a un derivado de S_t de precio v (S_t , t), y la proporción complementaria 1 – w_1t – w_2t que destina a la tenencia de capital, k_t . En consecuencia, la evolución de la acumulación de la riqueza real sigue la ecuación diferencial estocástica:

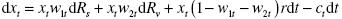
donde el rendimiento del activo con riesgo está dado por

y el rendimiento de su derivado por

El rendimiento del derivado se obtiene mediante la aplicación del lema de Itô a v (S_t , i),

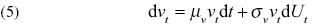
De tal forma que la restricción presupuestal se puede escribir como:

Se requiere especificar un pago al vencimiento del derivado, v(S_t ,T) = g (S_t ).

 

Posibilidades de producción

Suponga que el proceso de producción y, tiene la forma:

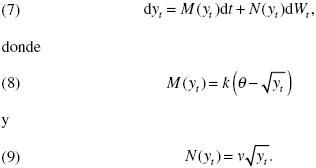
Las cantidades k, θ y v son constantes positivas y {W_t }es un movimiento Browniano definido sobre un espacio fijo de probabilidad (Ω^W, F^W, P^W) junto con su filtración aumentada F^W = {F_t }_{t ≥ 0}. Suponga también, por simplicidad, que Cov (dU_t , dW_t) = 0.

 

Problema de decisión del consumidor

Se supone que el consumidor representativo obtiene satisfacción por el consumo de un bien de carácter perecedero. En este caso, la utilidad esperada, V_t , al tiempo t de un individuo representativo, adverso al riesgo y competitivo (tomador de precios) tiene la siguiente forma:

donde c_s es el consumo al tiempo s, δ es la tasa subjetiva de descuento, y_s representa el impacto de la tecnología en la función de utilidad, y F_t es la información relevante disponible hasta el tiempo t. En este caso F_t ≡ F^_tW × F^_tU. Así pues, el consumidor desea determinar la trayectoria de consumo y las proporciones de su riqueza que va a asignar a los activos.

 

Condiciones de primer orden

En este caso, la condición de Hamilton–Jacobi–Bellman del problema de control óptimo estocástico de maximización de utilidad, sujeto a la restricción presupuestal, está dada por:

es la función de utilidad indirecta y J_a (x_t, y_t) es la variable de co–estado. Si se toma como candidato de solución a J (x_t , y_t , t) = H (x_t , y_t )e^–δt se tiene que la ecuación de Hamilton–Jacobi–Bellman se transforma en

En este caso, se satisface que H (x_t , y_t) = g ( y_t ) ln (x_t ) + f (y_t) para algunas funciones g ( y_t ) y f (y_t ). Después de derivar la ecuación (12) con respecto de las variables de control, la condición necesaria sobre el consumo es

y las condiciones de primer orden sobre w_1t , y w_2t son, respectivamente,

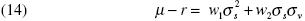
y

 

Las dos últimas ecuaciones pueden ser escritas en términos matriciales como:

donde ∏ = (l,l)^T.

 

Portafolio de equilibrio

Considere la solución de esquina dada por w₁ = 0 y w₂ = 0. En este caso, las condiciones (14) y (15) se transforman, respectivamente, en:

De la última ecuación se sigue que

Si se utiliza ahora la ecuación (16), se obtiene

 

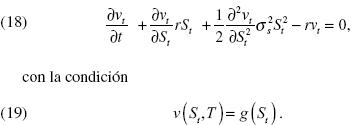
Un proceso alternativo para la tasa de interés de equilibrio

A continuación se presenta una fórmula alternativa para la tasa de interés de equilibrio. Observe que a partir de (16), se cumple que

En lo que sigue se supone que µ > σ^_s2. La tasa de interés de equilibrio satisface

donde w₁ = 1 y w₂ = 0. En efecto, es suficiente observar que

 

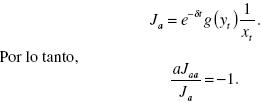
Dinámica de la tasa corta

En esta sección, a partir de un proceso para la función de producción, se determina la dinámica estocástica de la tasa corta. Si se definen en (20), se tiene que

 

 

Valuación de un bono cupón cero

Considere un mercado en donde los inversionistas compran y emiten promesas de pago de una unidad monetaria en el futuro, libres de riesgo crédito. Estas promesas que se compran a descuento serán llamadas bonos cupón cero. Sea B (t, T ) el precio en el tiempo t de un bono que se compra a descuento con vencimiento en el tiempo T, T > t , y que paga una unidad monetaria al vencimiento, es decir,

El precio de un bono cupón cero está dado por

El rendimiento al vencimiento o estructura de plazos o curva de rendimiento o, simplemente, curva de ceros, en el tiempo t de un bono con vencimiento T, está dada por:

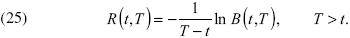
La tasa corta está descrita a través de una ecuación diferencial estocástica de la forma:

donde {W_t }_{0 ≤ t ≤ T} es un movimiento Browniano definido sobre un espacio fijo de probabilidad equipado con una filtración (Ω^W,F^W,P^W). De acuerdo con (23), las funciones α ( r_t , t) y β ( r_t, t) están dadas por

Conclusiones

Se ha desarrollado un modelo de equilibrio general en una economía estocástica poblada por consumidores–inversionistas idénticos, competitivos y adversos al riesgo para determinar el precio de un derivado y el precio de un bono cupón cero. El modelo propuesto proporciona dinámicas alternativas de equilibrio para la tasa corta a las obtenidas en Cox, Ingersoll y Ross (1985b) y generaliza el modelo de tasa corta de Longstaff (1989). Por último es importante mencionar que el modelo puede ser extendido en varias direcciones: falta incorporar volatilidad estocástica y considerar otras formas funcionales comunes para la función de utilidad.

 

Bibliografía

Cox, J., J. Ingersoll y S. Ross (1985a). "An intertemporal general equilibrium model of asset prices", Econometrica, 53(2), pp. 385–467.         [ Links ]

Cox, J. y S. Ross (1985b). "A theory of the term structure of interest rates", Econometrica, 53(2), pp. 385–467.         [ Links ]

Grinols, E. L. y S. J. Turnovsky (1993). "Risk, the financial market, and macroeconomic equilibrium", Journal of Economic Dynamics and Control, 17(1–2), pp. 1–36.         [ Links ]

Lee, M. y W. Li (2005). "Drift and diffusion function specification for short–term interest rates", Economic Letters, 86(3), pp. 339–346.         [ Links ]

Longstaff, F. A. (1989). "A nonlinear general equilibrium model of the term structure of interest rates", Journal of Financial Economics, 23(2), pp. 195–224.         [ Links ]

Schmedders, K. (1998). "Computing equilibria in the general equilibrium model with incomplete asset markets", Journal of Economic Dynamics and Control, 22 (8–9), pp. 1375–1401.         [ Links ]

Turnovsky, S. J. (1986). "Short–term and long–term interest rates in a monetary model of a small open economy", Journal of International Economics, 20 (3–4), pp. 291–311.         [ Links ]

Venegas–Martínez, F. (2001). "Temporary stabilization: a stochastic analysis", Journal of Economic Dynamics and Control, 25(9), pp. 1429–1449.         [ Links ]

Venegas–Martínez, F. y B. González–Aréchiga (2002). "Cobertura de tasas de interés con futuros del mercado mexicano de derivados: un modelo estocástico de duración y convexidad", El Trimestre Económico, 59(2) No. 274, pp. 227–250.         [ Links ]

Venegas–Martínez, F. (2006). "Stochastic Temporary Stabilization: Undiversifable Devaluation and Income Risks", Economic Modelling, 23(1), pp. 157–173.         [ Links ]

Venegas–Martínez, F. (2006a). "Fiscal Policy in a Stochastic Temporary Stabilization Model: Undiversifable Devaluation Risk", Journal of World Economic Review, 1(1), pp. 87–106.         [ Links ]