Artículos

 

Unicidad del equilibrio de Nash-Cournot bajo correspondencias contractivas de mejor respuesta

 

Elvio Accinelli¹ y Edgar J. Sánchez Carrera²

 

¹ Professor of Economics at Universidad Autónoma de San Luis Potosí, Mexico. PhD in Applied Mathematics for Economics, IMPA Brasil. E-mail: elvio.accine-li@eco.uaslp.mx.

² Current Ph. D. Student at Department of Economics, University of Siena, Italy. M.Sc. in Economics at University of Siena, Facoltá di Economía, Richard M. Goodwin. University of Siena, ITALY. E-mail: sanchezcarre@unisi.it.

 

Resumen

En este trabajo se muestran condiciones para la unicidad del equilibrio de Nash-Cournot para un juego de n-firmas. Estas condiciones garantizan que las funciones de mejor respuesta para n-firmas que compiten en forma oligopólica a la Cournot sean contracciones y generalizan las condiciones de concavidad generalmente consideradas para este fin.

Palabras clave: mejor respuesta, contracción, equilibrio de Cournot, unicidad.

Clasificación JEL: C02, C60, C72, L13.

 

Abstract

In this work we obtain new conditions to reach the uniqueness of Nash equilibrium in a Cournot oligopoly model. These conditions assure that the reaction functions are contractions and they are not reduced to the obtained ones by Rosen (1965), in as much as they do not demand the strict concavity of the benefit functions

 

Introducción

La teoría de juegos trata situaciones de conflicto y negociación. Una situación de conflicto supone una interacción entre dos o más individuos (jugadores) que actúan recíprocamente y donde las acciones elegidas por cada uno para resolver la situación determinan un resultado final al conflicto, sin que cada uno pueda asegurar por sí mismo el resultado final. Cada uno participando como jugador puede controlar la situación parcialmente, pero ningún jugador tiene mando completo. Cada jugador tiene preferencias sobre los posibles resultados del juego y escoge una estrategia con el objetivo de obtener el resultado más beneficioso posible para él, tomando en cuenta las elecciones estratégicas de los demás jugadores. Tales preferencias pueden describirse como una función de utilidad esperada (a la von Neumann-Morgenstern), en la cual cada jugador se caracteriza por una función numérica cuyo valor esperado es el que intenta incrementar al máximo.

Un equilibrio de Nash (Nash, J., 1951) es una combinación estratégica con la propiedad de que ningún jugador puede ganar o mejorar desviándose unilateralmente de tal combinación. El equilibrio de Nash puede caracterizarse por ser, para cada jugador, una mejor respuesta, dadas las estrategias elegidas por los demás. Un juego puede poseer más de un equilibrio de Nash; en este caso, el estudio de las características de estos equilibrios es central para poder entender las soluciones posibles (ver por ejemplo Van Damme, 1991). Dada la complejidad de esta discusión, obtener condiciones amplias que garantizan la unicidad local del equilibrio de Nash no es de menor importancia.

En condiciones muy generales, la existencia del equilibrio de Nash está garantizada. Nuestro objetivo es obtener condiciones amplias que impliquen la unicidad del equilibrio de Nash. En la literatura es conocido que si las reacciones son funciones contractivas, la unicidad del equilibrio se sigue (el uso de la propiedad de contracción para asegurar la unicidad del equilibrio de Nash, tiene como referencia inicial a Debreu (1952), y una aproximación diversa se da con la condición de concavidad de las funciones de reacción, en Rosen (1965). El estudio de unicidad del equilibrio en mercados oligopólicos está ampliamente tratado por Vives (1999), considerando el teorema de punto fijo para contracciones. Sin embargo, en nuestro trabajo presentaremos condiciones sobre las funciones de utilidad que garantizan la unicidad del equilibrio de Nash y que, de alguna manera, generalizan las presentadas en Rosen por cuanto, en principio, no exigen concavidad de las funciones de utilidad. A diferencia de los trabajos realizados por Kohlstad y Mathiesen (1987) y Long y Soubeyran (2000), nuestro desarrollo puede aplicarse a diversos casos, n-firmas oligopólicas, duopolios y competencia a la Hotteling (empresas compitiendo vía precios en una ciudad lineal, Hotelling, 1929). Así, discutiremos a partir del teorema de unicidad por contracción en el caso de competencia oligopólica.² Veremos también que a medida que el número de agentes en el juego aumenta, las condiciones que aseguran la unicidad del equilibrio de Nash-Cournot se hacen cada vez más restricitivas. No obstante, en las condiciones habituales para dos jugadores, esta condición se cumple automáticamente.

El presente artículo está constituido de la siguiente manera: la sección 2 describe las características esenciales del teorema de punto fijo para contracciones. La sección 3 formula las condiciones para la unicidad del equilibrio de Nash. La sección 4 es el núcleo del trabajo. Se muestra un teorema para la unicidad del equilibrio de Nash-Cournot, considerando a la función de mejor respuesta como una contracción; además se muestra la unicidad del equilibrio de Nash para la competencia de Hotelling. Mostraremos que los axiomas del teorema de Rosen, en determinados casos, aseguran esta propiedad de la función de mejor respuesta. Sin embargo, nuestro resultado no se sigue de los obtenidos por Rosen. En la sección 5 se presentan los comentarios finales.

 

El teorema de contracción

Recordemos algunos conceptos básicos relacionados con los espacios métricos.

Definición 1. Un espacio métrico es un par (X,d) donde X es un conjunto no vacío y d es una función real definida en X x X, llamada distancia o métrica, y que satisface los siguientes axiomas: i) d(x,y)≥0 _x,y∈X, y d(x,y)=0_x=y, ii) d(x,y)=d(y,x)_x,y_X, y iii) d(x,z)≤d(x,y)+d(y,z) _x,y,z_X.

Es decir, i) las distancias son no negativas y el único punto a distancia cero de x es el mismo x; ii) la distancia es una función simétrica; y iii) la distancia satisface la desigualdad triangular: la longitud de un lado de un triángulo es menor que la suma de las longitudes de los otros dos lados.

Para un dado conjunto X es posible definir más de una métrica. Cuando la métrica del espacio se da por sobreentendida, se habla simplemente del espacio métrico X aunque sabemos que realmente éste es un par (X,d). Los elementos de X son llamados puntos del espacio métrico.

Definición 2. Supongamos que x, y∈ R^m . La distancia desde x hasta y, representadas bien como d(x,y) o ||x-y||, es d(x, y) = max_i |x_i-y_i|

Definición 3. Sea (X,d) un espacio métrico. Una función ƒ : X _ X es una contracción si existe una constante k con 0≤k<1 tal que

Por lo tanto, una contracción acerca los puntos del espacio métrico. Dicho de forma simple, una contracción deja las imágenes de dos puntos más cerca de lo que lo estaban los puntos originales. De la ecuación (1) se deduce que una contracción es uniformemente continua.

Por lo tanto, si ƒ: X _ X, entonces un punto x_X tal que ƒ(x)=x, que es llamado un punto fijo de ƒ. El teorema de la contracción dice que una contracción en un espacio métrico completo tiene un único punto fijo. Es decir, si ƒ: X _ X es una contracción en un espacio métrico completo (X,d), entonces existe exactamente una única solución x_X de la ecuación

Teorema de punto fijo para contracciones. Sea un X ⊆ R^m subconjunto cerrado y ƒ: X _ X una contracción. Dado cualquier punto x_X, la sucesión converge x_n+1 = ƒ(x_n) para un punto x_X que es el único punto fijo de ƒ. Una demostración clara se puede ver en Accinelli (2005b) y Lima (1981).

 

Unicidad del equilibrio de Nash

Un juego no cooperativo se caracteriza por:

i. Los jugadores no tienen capacidad para llegar a acuerdos vinculantes.

ii. Cada jugador sabe lo que el otro sabe y a su vez sabe que su oponente sabe lo que él sabe.

iii. Los jugadores no podrán intercambiar información ni ningún tipo de dato en el transcurso del juego.

Definición 4. Un juego n-personal finito en forma normal se define como una terna donde: i) N={1,...,n} es un conjunto finito de jugadores, ii) para cada i_N, A_i es un conjunto de acciones posibles de ser elegidas (espacios de estrategias puras) y, iii) P:A → R, donde A = A₁ x...xA_n es una función de retorno o pagos.

Las siguientes hipótesis garantizan la existencia del equilibrio de Nash:

i. A_i ⊂ : Rⁿ es compacto y convexo para cada i_N.

ii. P_i (α) ∈ R está definido, es continuo y acotado para todo α ∈ A, i ∈ N.

iii. P_i (α_i, α__i) es concavo con respecto a α_i∈ A¡ para todo α ∈ A, i ∈ N.

Por consiguiente, un punto de equilibrio es una combinación estratégica, α*, que es factible (es decir, que se halla contenida en A) y para el que cada jugador maximiza su beneficio o pago con respecto a su propia elección estratégica, dadas las elecciones estratégicas de los otros jugadores.

Definición 5. El equilibrio de Nash del juego _ = (N,A,P) es una combinacion α* ∈ A de acciones tal que:

Es decir, el equilibrio de Nash es un vector estratégico que garantiza la no existencia de incentivos para cambiar unilateralmente la estrategia α*.

Para cada α__i ∈ A__i definimos el conjunto de mejores acciones del jugador i dadas las acciones α__i elegidas por los otros jugadores, como:

Definición 6. La correspondencia de mejor respuesta del jugador i, llamado el conjunto de mejores respuestas B_i, satisface que el equilibrio de Nash es un vector α* de acciones para las cuales

Definimos B : A _ A la correspondencia B(α) = (B₁(α_₁), ...,B_n(α__n)), donde 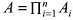a la que llamaremos corespondencia mejor respuesta.

Como hemos mencionado, una de las primeras contribuciones sobre la unicidad del equilibrio de Nash se debe a J. B. Rosen, en 1965, quien propone la consideración de características de concavidad para las funciones de retorno, se define, entonces, un juego cóncavo. Esto es, se tendrá un único punto de equilibrio para cada juego estrictamente cóncavo. Esto muestra que, para un juego estrictamente cóncavo, el sistema es globalmente y asintóticamente estable con respecto al único punto de equilibrio del juego.

El teorema de unicidad del equilibrio de Nash que presentaremos es independiente al dado por Rosen y, como veremos, aplica a casos no cóncavos. Como es bien conocido, un equilibrio de Nash es un punto fijo de la correspondencia mejor respuesta. El teorema de Kakutani asegura la existencia de al menos un punto fijo para este juego. Presentamos a continuación la demostración de que si la correspondencia de mejor respuesta es contractiva, entonces existe un único equilibrio de Nash.

Teorema 1. (Unicidad del equilibrio de Nash) Sea _=(N,A,P) un juego en forma normal de n jugadores, en las condiciones previamente definidas. Si la función de mejor repuesta es una contracción entonces existe un único equilibro de Nash.

Demostración: Supongamos que la correspondencia mejor respuesta B es una contracción. Sean α', α" ∈ A dos equilibrios de Nash diferentes, (es decir que, α' ∈ B(α') y α" ∈ B(α")). Luego d(B(α'), B(α")) = d(α', α") por ser B(_) una contracción, se sigue que d(B(α'), B(α")) ≤ kd(α', α"). Siendo k < 1, se sigue que α' = α".

 

Unicidad del equilibrio de Nash-Cournot

En lo que sigue mostraremos, para el caso de competencia oligopólica con N-firmas, condiciones que aseguran que la correspondencia mejor respuesta sea una contracción. Si exigimos la estricta concavidad de las funciones de utilidad, las condiciones de Rosen se cumplen y, por lo tanto, la unicidad del equilibrio de Nash se sigue. Obtendremos a continuación condiciones para la unicidad trabajando directamente a partir de las funciones mejor respuesta.

Primeramente analizamos un caso sencillo de 2 competidores. Veremos que, bajo las hipótesis habituales, la correspondencia de mejor respuesta es una contracción y luego lo generalizamos a N competidores.

Se considera una industria compuesta por dos empresas con una función de costos para cada firma i (produciendo q_i unidades) dada por: Consideremos una rama industrial oligopolizada compuesta por dos firmas, a las que representaremos por i=1,2. Las respectivas funciones de costos serán C_i : A_i → R donde A_i = [0, Q_i], i = 1, 2, representa un subconjunto compacto y conexo de R. Por A_i = [0, Q_i],i = 1, 2, representamos la cantidad del bien que la i-ésima firma elige producir. En defintiva es el conjunto de estrategias puras posibles para cada firma.

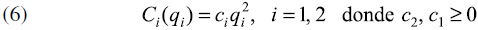
La correspondiente función de demanda inversa es conocida por las firmas y la representamos por:

Cada firma elige q_i ∈ A¡ =[0, Q_i], i = 1, 2. La función de retornos de cada firma está representada por p_i(q₁, q₂) = p(Q)q_i - C_i(q_i) El perfil estratégico q* = (q*₁, q*₂) será un equilibro de Nash-Cournot si:

Así, obtenemos:

De esta forma, un equilibrio de Nash-Cournot queda definido por las acciones elegidas por las firmas, de forma tal que ninguna tiene incentivos a desviarse y en conjunto definen el precio unitario:

Resolviendo (7), obtenemos q_i en función de q_j, donde i ≠ j e i, j ∈ {1, 2}. Esto permite definir la función de mejor respuesta para la firma i la que representaremos por B_i(q_j). Para simplificar consideremos el caso en que c_i(q_i) = c_i q_i, i = 1,2. Entonces:

Veamos ahora que bajo las condiciones habituales, la correspondencia de mejor respuesta es una contracción. Consideremos que 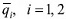es solución de (8) y (9). Una función B : R² _ R² es una contracción si existe una constante k 0≤k<1 tal que, , ∀i = 1,2 se tiene entonces que:

Con de acuerdo a las hipótesis c≥;0 and b>0, implica que 2(b+c)>b. Por lo tanto, 0<k<1. Así, la correspondencia mejor respuesta es una contracción.

El caso del oligopolio de Cournot con N firmas

La idea central del modelo generalizado de Cournot está basada en el supuesto de que un conjunto de N firmas racionales compiten simultáneamente en la provisión de un mismo mercado oligopolístico. Las firmas conocen la función de demanda. La cantidad agregada producida y vendida determina instantáneamente el equilibrio de mercado.

En este apartado seguiremos el modelo propuesto por Accinelli (2005a), donde suponemos un juego en forma estratégica, con N firmas que deben elegir simultáneamente la cantidad de un producto que lanzarán al mercado. Los productos son substitutos perfectos. Suponemos que cada firma i_{1,...,n}, elige la cantidad a producir en el intervalo . La función de costos está dada por C_i(q_i).

La estructura analítica del modelo responde a una función de inversa demanda p : [0,Q_i] _ R, donde p es el precio y Q es el total posible de producción agregada, .

Representaremos al vector estratégico q como (q_i, q__i), indicando que la i-ésima firma elige su estrategia q_i ∈ A_i como respuesta a la elección de las otras firmas, la que se representa por .

Los pagos que reciben las firmas se determinan por las funciones de beneficios, . Sea p(Q) = a-bQ, la función inversa de demanda. La función de beneficios de la i-ésima firma quedará representada por:

Representaremos por Q la producción agregada asociada a la elección estratégiga q = (q_i, q__i), es decir:

El concepto de equilibrio de Nash-Cournot en este mercado se caracteriza por un vector de producción q* = (q*₁, q*_n)tal que ninguna firma tiene interés en desviarse. Es decir, π_i(q*_i, q*_-i) ≥ π_i(q*_i, q*_-i) ∀q_i∈ A_i. Por consiguiente, la correspondencia de mejor respuesta para cada firma está definida por:

A partir de la cuasi-concavidad de las funciones de beneficio para las firmas, y la compacidad del espacio de estrategias, el teorema del máximo asegura que para cada firma su correspondencia de mejor respuesta es semicontinua superior y compacta y, por consecuencia, el Teorema de Kakutani y Teorema 1 aseguran la existencia del equilibrio de Nash para el modelo de Cournot.

El siguiente teorema asegura que la correspondencia de mejor respuesta es una contracción. Lo cual implica unicidad del equilibrio de Nash-Cournot.

Teorema 2 (De unicidad local). Todo juego de Cournot _=(N,Q,π) en las condiciones previamente definidas, si la correspondencia de mejor respuesta verifica que

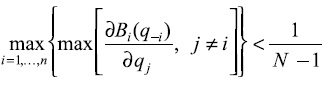
tiene unicidad de equilibrio.

Demostración: A partir de las condiciones de primer orden se tiene que:

Las funciones son diferenciables con con respecto a las N variables q_i, i = 1,2,...,N. Sea una solución de (13). Supongamos que las derivadas 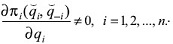El teorema de la función implícita nos dice entonces (ver detalles, ejemplo Apóstol, 1991), que para cada i existen entornos de tales que para cada existe un único q_i(q__i) tal que (q_i(q__i),q__i)∈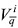 y . Se obtiene entonces que el sistema de ecuaciones funcionales con N variables

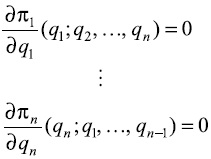
puede ser resuelto en el entorno 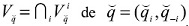Se obtienen entonces las correspondencias de reacción: B_i : Rⁿ → R, i = 1,2,..., n siendo q_i,..., q_i-1, q_i+1,..., q_n) = B_i(q__i), las que son diferenciables.

Para cada B_i(q__i) definimos el gradiente evaluado en como:

donde D_q-i={D_q1,...,D_q1-i,D_q1+i,...,D_qn}, es el operador de derivadas parciales, en este caso aplicado a π respecto a las variables q_j, j ≠ i, de esta forma obtenemos el gradiente de la reacción de la firma i para el caso considerado como:

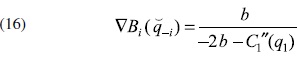
A partir del teorema del valor medio y la desigualdad de Cauchy-Schwarz, mostraremos que la correspondencia mejor respuesta es una contracción. Sean dos vectores estratégicos en 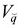, entonces:

Con el uso del teorema del valor medio escribimos:

donde q_—i0 = (q__i+θh) con _(0,1). Usando la desigualdad de Cauchy-Schwarz, obtenemos:

Sea entonces, a partir de (19), se tiene:

Así, la desigualdad se obtiene:

donde . La desigualdad anterior puede escribirse como:

Se concluye que la correspondencia mejor respuesta es una contracción si se verifica que: , es decir, si para todo i=1,2,...,n se tiene:

Es ésta entonces una condición para la unicidad local del equilibrio de Nash-Cournot[+].

Obsérvese que el teorema de la función implícita permite definir a cada coordenada de la correspondencia mejor respuesta como una función derivable, tal que q_i =q_i(q__i) para todo q_i = B_i(q__i) solamente en un entorno de una solución del sistema (13), por lo que obtenemos solamente condiciones para la unicidad local. No obstante, si asumimos la existencia de esta función de mejor respuesta como una función derivable, lo que es común a la mayoría de las aplicaciones, entonces podemos enunciar un teorema de unicidad global.

Teorema 3 (De unicidad global). Todo juego de Cournot _=(N,Q,π) en las condiciones previamente definidas, en el que las coordenadas de la correspondencia mejor repuesta son funciones B_i: A__i → A_i, i=1,..., n, definidas como q_i= B_i(q__i), i=1,...,n derivables y verifican

tiene unicidad (global) de equilibrio.

Demostración: Una vez asumida la existencia de una correspondencia de mejor respuesta como una función derivable con respecto a todas sus variables, la demostración del teorema sigue como en (2)[+].

Para nuestro caso se concluye que si se verifica:

entonces hay unicidad de equilibrio.

Equivalentemente, si -2b-C_(q) > 0 la condición de equilibrio es:

y si -2b-C_(q) < 0 dicha condición está dada por:

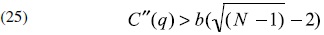
Observe que si C es una función convexa como generalmente ocurre en teoría económica, entonces debemos considerar la condición (25). Por lo que si el número de participantes crece, entonces la condición de unicidad es más restrictiva; no obstante, la condición se obtiene inmediatamente para el caso N = 2, lo que afirma la unicidad el equilibrio en estos casos.

 

Competencia de Hotteling

Como aplicación veamos condiciones que garantizan la unicidad de la solución del modelo de competencia de Hotteling. Tomemos el ejemplo de una ciudad lineal, es decir, supongamos una calle de longitud 1 en la que se encuentran distribuidos uniformemente H consumidores, existen dos firmas en lugares extremos de la calle, que producen el mismo bien.

Supongamos que la distancia entre las firmas es igual a 1. La firma 1 está ubicada en x = 0, la firma 2 en x = 1. El costo unitario del producto para cada firma es c. Los consumidores incurren en un costo de transporte igual a t por unidad de distancia recorrida. Sea p_i el precio al que la firma i = 1,2 ofrece su producto. Los consumidores recurrirán para comprar una unidad del producto a la firma 1 o 2, según el costo sea menor. El costo unitario para el consumidor está dado por p₁ + tx donde x es la distancia a la firma 1 si recurre a la firma 1, y p₂ + (1 - x)t si recurre a la firma 2.

Suponemos que la demanda para la firma i = 1 está representada por D₁(p₁,p₂) = donde está definida por la igualdad p₁+t=p₂+t(1-). Se sigue entonces que la demanda que enfrenta la firma 1 es:

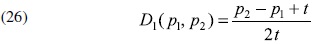
y la demanda correspondiente a la firma 2 es:

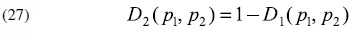
Supongamos que las firmas eligen precios en forma simultánea, lo que permite modelar la situación como un juego normal de una sola vez. Consecuentemente, el equilibrio de Nash es un perfil estratégico (p*₁,p*₂) tal que

El problema de maximización que resuelve la firma 1 es:

La correspondencia mejor respuesta para esta firma está dada por:

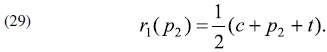
Análogamente para la firma 2:

El equilibrio competitivo para el modelo de Hotelling es entonces un equilibrio de Nash. La correspondencia mejor respuesta es una contracción con k = 1/2 pues como fácilmente puede comprobarse . Entonces, la solución es única. Tal solución es: p*₁ = p*₂= c + 3t/ 2.

 

Conclusiones

En definitiva, la unicidad del equilibrio depende de las características estructurales del modelo que estamos analizando. Si bien la estricta concavidad de las utilidades asegura en determinadas condiciones la unicidad del equilibrio, hemos probado que es posible relajar esta condición sin que la unicidad se pierda. Si bien es cierto que, en el modelo que presentamos, las condiciones que garantizan que las funciones de reacción sean contracciones, y en definitiva la unicidad del equilibrio, no dependen de la concavidad de las utilidades, aunque sí dependen del número de jugadores, haciéndose cada vez más difíciles de obtener. No obstante, esto ofrece una nueva perspectiva. El caso simple presentado como modelo de competencia de Hotteling muestra posibilidades de extender las aplicaciones; asimismo, a partir de esta presentación puede pensarse en modelos a la Hotteling generalizados, donde los productos ofrecidos sean sustitutos y no el mismo; de esta forma, la reacción ya no será lineal en los precios, sino más bien función de los precios y parece ser posible encontrar condiciones sobre esta función que aseguren unicidad del equilibrio en situaciones más realistas.

El teorema de unicidad del equilibrio de Nash propuesto por Rosen se basa en una extensión de las condiciones de concavidad y hace uso de la diferenciabilidad. Sin embargo, el teorema de unicidad por contracción aquí presentado no requiere la diferenciabilidad de las funciones de utilidad, mientras que el teorema de Rosen requiere que las segundas derivadas parciales sean continuas. El teorema de unicidad del equilibrio de Nash por contracciones, que ha sido desarrollado en este trabajo, es aplicable para diferentes casos, es sencillo y no es tan restrictivo en las condiciones que se requieren para tener la contractividad de las funciones de mejor respuesta.

 

Bibliografía

Accinelli, E. (2005a). Elementos de Topología y de la Teoría de Conjuntos en la Teoría del Equilibrio General. Universidad Autónoma Metropolitana, México. Ediciones EON.         [ Links ]

Accinelli, E. (2005b). "La Topología de las Correspondencias y el equilibrio de Nash", en Economía Aplicada, Economía Dinámica y Teoría de Juegos. Ensayos en Homenaje a Ramón García-Cobián", editado por César Martinelli y Loretta Gasco. Pontificia Universidad Católica del Perú         [ Links ].

Apostol, T. M. (1991), Mathematical Analysis, California Institute of Technology. Reading, Massachusetts.         [ Links ]

Debreu, A. (1952). Social Equilibrium Existence Theorem, Proceeding of the National Academy of Sciences.         [ Links ]

Hotelling (1929). "Stability in competition", Economic Journal 39:41-57.         [ Links ]

Kohlstad C. D. y Mathiesen L. (1987). "Necessary and Sufficient Conditions for Uniqueness of Cournot Equilibrium", Review of Economic Studies, 54, 681-690.         [ Links ]

Lima, E. (1981), Curso de Análise, Vol. 2 Ed. IMPA, Projeto Euclides.         [ Links ]

Long N. van y Soubeyran A. (2000). "Existence and Uniqueness of a Cournot equilibrium: a contraction mapping approach", Economic Letters, 67, 345-348.         [ Links ]

Nash, John F., Jr. (1951). "Non-Cooperative Games", Annals of Mathematics 54:286-295.         [ Links ]

Rosen, J. B. (1965). "Existence and Uniqueness of Equilibrium Points for Concave n-Person Games", Econométrica 33:520-534.         [ Links ]

Segura, J. (1992). Teoría de la Economía Industrial, Biblioteca Civitas Economía y Empresa.         [ Links ]

Van Damme, E. (1991). Stability and Perfection of Nash Equilibria, Spriger-Verlag.         [ Links ]

Vives, X. (1999). Oligopoly Theory, Cambridge University Press.         [ Links ]

 

Nota

² Recomendamos Segura (1992) para el estudio de mercados imperfectos.