PACS: 01.40.Ha; 01.50.Wg; 03.67.Lx; 07.05.Hd
1. Introducción
En los últimos años, se ha intensificado la construcción y uso de cohetes hidráulicos 1,2,3,4,5,6,7,8,9 como una herramienta innovadora para el aprendizaje de la física al interior del aula de clases 9,10,11,12,13,14,15,16. El movimiento de cuerpos auto-propulsados es un tema de alto interés, presentado en los cursos de física básica y ejemplifica las leyes de Newton aplicadas a un sistema de masa variable 17,18,19,20.
Una revisión bibliográfica refleja una vasta literatura disponible, que describe el movimiento del cohete bajo distintas consideraciones físicas 1,2,3,4,21,22,23,24,25,26,27,28,29, sin embargo, en ningún trabajo se presenta un análisis cinemático bi-dimensional de este sistema a partir de datos experimentales a una resolución de tiempo del orden de mili-segundos
Con la aparición de las cámaras fotográficas digitales de alta velocidad, es posible grabar objetos en movimiento en vídeo a velocidades superiores a los 25 fps (“cuadros por segundo”, por sus siglas en ingles). Con la ayuda de software especializado como “Tracker” 30, se pueden analizar estas grabaciones y obtener información física del movimiento de dicho objeto 31,32,33,34,35.
En este trabajo se analizan los videos del despegue de cuatro (4) cohetes hidráulicos, grabados con una cámara Nikon 1J1 36 a una velocidad de 400 fps. La posición del cohete para un cierto tiempo t se obtienen al procesar el video con el programa “Tracker”. Con estos datos, se construye un modelo físico del sistema, empleando un ajuste a un polinomio de cuarto grado a través del método de mínimos cuadrados.
Esta actividad experimental puede ser replicada en un curso de física a nivel de preparatoria y primeros semestres a nivel universitario en carreras de ciencias e ingeniería, buscando que los estudiantes puedan construir modelos físicos sencillos a partir de datos experimentales, además de estudiar sistemas en los cuales la aceleración y la masa son variables.
2. Etapas del vuelo de un Cohete hidráulico
En el estudio del vuelo de un cohete de agua, es posible identificar tres etapas:
Propulsión con agua: El cohete contiene agua y aire a una presión inicial y por ello el peso del sistema es significativo. Al disparar el cohete, este expulsa el agua a través de la boquilla de la botella, con una velocidad que depende de la presión del aire. El agua expulsada proporciona un empuje de propulsión que aumenta el impulso del cohete asociado a una disminución en su masa. La presión del aire va disminuyendo, reduciendo la velocidad de salida del agua y el empuje de propulsión. En contraste, la velocidad y la fuerza de arrastre se incrementan. La propulsión del agua dura hasta que todo el volumen de agua ha sido expulsado de la botella.
Propulsión con aire: El aire que permanece dentro del cohete al final de la etapa anterior se encuentra aun presurizado, lo que provoca un empuje adicional en el cohete al ser expulsado. Este efecto generalmente no es considerado en un sencillo análisis teórico, sin embargo, el incremento en el momento lineal del cohete puede ser significativo dependiendo de la magnitud de la presión del aire restante, debido a que el peso del cohete en este punto es pequeño.
Vuelo libre: Al final de la etapa de propulsión con aire, el cohete está vacío (o, de hecho, lleno de aire a presión atmosférica) y realiza un vuelo completamente balístico.
En este trabajo, se analiza el vuelo del cohete en la primera etapa de propulsión con agua.
3. Modelo físico
El cohete hidráulico está constituido por una botella de plástico PET, parcialmente llena de agua y aire a presión. La botella se encuentra invertida, es decir, con la boca hacia abajo en una plataforma de lanzamiento. Al ingresar el aire a presión y accionar el sistema de lanzamiento, el agua es expulsada de la botella a una alta velocidad. Como reacción, la botella se eleva.
Este dispositivo es un ejemplo por excelencia de un sistema de masa variable, el cual ha sido estudiado en la gran mayoría de libros de texto de física a nivel universitario 17,18,19,20.
La dinámica de un cohete de agua puede ser investigada analizando las fuerzas que lo afectan, que incluyen las debidas a la resistencia aerodinámica (drag), la fuerza de atracción gravitacional (peso) y el empuje debido al agua expulsada, las cuales se aprecian en la Fig. 1.
Considerando la segunda ley de Newton en su forma más general:
la razón de cambio de la cantidad de momento del cohete respecto al tiempo esta dada por:
donde mc es la masa del cohete (botella, alas y punta aerodinámica), ρ es la densidad del fluido expulsado por el cohete (agua + aire), el cual varía con el tiempo, dV es el diferencial de volumen, (u + v) es la velocidad del fluido respecto al suelo, u es la velocidad del fluido relativo a la botella y v es la velocidad del cohete para un instante de tiempo t. Considerando todas las interacciones sobre el cohete se tiene:
Donde (Pexp - Patm) es la diferencia de presión entre el fluido expulsado y la presión atmosférica, Aexp es el área del orificio por donde se expulsa el fluido en el cohete, Fdrag es la resistencia aerodinámica o drag,
es la masa total del cohete (botella + alas + punta + agua + aire) para cualquier instante de tiempo
4. Experimento
Para este experimento, se construyeron un total de 4 cohetes, empleando botellas de refresco con una capacidad de 2 litros. Se utiliza el mismo tipo de botellas para su fabricación, de superficie liza, con el fín de minimizar la rotación de los cohetes debido al efecto Magnus con el aire 1,2. Las alas se ubicaron en la parte inferior del cohete (como se observa en la Fig. 2), con dimensiones que están en el rango de 70 mm a 100 mm de altura y 40 mm a 64 mm de ancho 6, esto con el objeto de que el cohete pueda alcanzar una alta velocidad y gran estabilidad en su vuelo 3.

Figura 2. Cohete y plataforma de lanzamiento por sujeción de cables (Clark cable-tie launcher) empleada en el experimento.
La plataforma de lanzamiento se construyó empleando el principio de sujeción de cables (Clark cable-tie launcher) desarrollada por Ian Clark 44, el cual ha sido ampliamente utilizado por la comunidad que realiza lanzamientos de cohetes hidráulicos. En la Fig. 2 se presenta la plataforma de lanzamiento empleada en este experimento. Todos los videos del despegue de los cohetes se grabaron con una cámara fotográfica Nikon 1 J1, a una velocidad de 400 fps y una distancia de separación de 50 cm de la plataforma de lanzamiento. En las Figs. 3-6 se presentan distintos instantes del vuelo de cada uno de los cohetes en condiciones de presión de lanzamiento de 50 psi y 80 psi, las cuales fueron medidas con el pequeño manómetro incorporado en la bomba de aire.
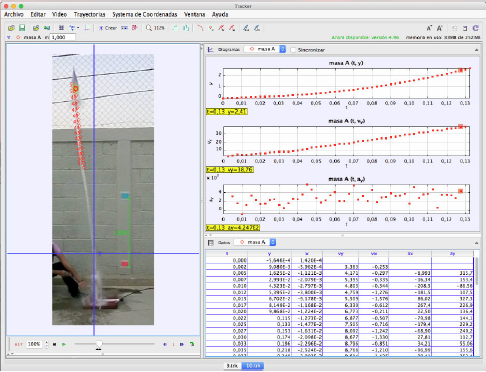
El movimiento de cada cohete se determina al analizar cada video de su despegue, usando el programa ‘Tracker’’, tal como se aprecia en la Fig. 7. Los videos fueron grabados empleando un tripode, con el fin de garantizar que en el análisis del video no aparezcan errores sistemáticos debido a los posibles cambios de posición de la cámara. Con el fin de identificar con mayor claridad la posición del cohete durante su vuelo, se agrega sobre su superficie un rectángulo de un color que resalte y permitan ubicarlo en cualquier instante de tiempo. La posición del cohete será la posición del punto medio de este rectángulo.
Es necesario realizar una calibración que permita al programa asociar la escala en píxels a una escala en metros, para ello se ubicaron dos rectángulos con una separación entre sus centros de 1 m en la pared opuesta al lugar de lanzamiento. Tracker permite obtener a partir del video las coordenadas en el plano xy de la posición del cohete para cada instante de tiempo. Con estos datos se realiza un ajuste polinomial de cuarto grado por el método de mínimos cuadrados. A partir de la ecuación de posición, se obtiene por derivación las ecuaciones de velocidad y aceleración del cohete en cada coordenada. Debido a que no es de nuestro interés realizar una descripción precisa y completamente detallada de este sistema, se dejará de lado el tratamiento de las incertidumbres en este experimento.
5. Resultados
El lanzamiento completamente vertical de un cohete hidráulico ofrece una gran dificultad técnica. La velocidad del viento, las variaciones de temperatura del medio ambiente, el movimiento de la plataforma de lanzamiento, la fuerza de Coriosis 45 entre otros factores, no son considerados en la mayoría de los modelos físicos convencionales que describen el movimiento de los cohetes hidráulicos. En contraste, los datos experimentales obtenidos en este trabajo incluyen de forma implícita estos efectos.
Algunos autores han propuesto que estos efectos se pueden describir al ajustar los resultados experimentales a funciones logarítmicas 41, polinomios de sexto grado 4, cuarto grado 37 y tercer grado 43 considerando únicamente el efecto del drag sobre el cohete. Al tener un conjunto de n parejas de datos, estos pueden ser ajustados hasta un polinomio de grado n, con un factor de correlación igual a 1. Aunque matemáticamente, este procedimiento puede ser correcto, físicamente deja de ser útil, ya que la oscilación del polinomio es tal que su predictibilidad está limitada exclusivamente a los puntos ajustados. Las soluciones numéricas a este problema sugieren que el mejor ajuste para un sistema como el cohete hidráulico es un polinomio de cuarto orden 37. Debido a que la trayectoria de los cohetes no es completamente vertical, separamos en cada eje el comportamiento horizontal y vertical del cohete en función del tiempo, con ayuda de Tracker.
En las Figs. 8 y 9 se presentan los resultados de posición en los ejes x y y para los cuatro cohetes hidráulicos, con su respectivo ajuste por el método de mínimos cuadrados a un polinomio de cuarto grado. Este método permite construir un modelo matemático que describe el comportamiento del cohete para su primera etapa de despegue. A partir de las ecuaciones de posición en función del tiempo, se obtiene por derivación las ecuaciones de velocidad y aceleración para cada cohete en la dirección x y y, las cuales se presentan en las Tablas I-IV.
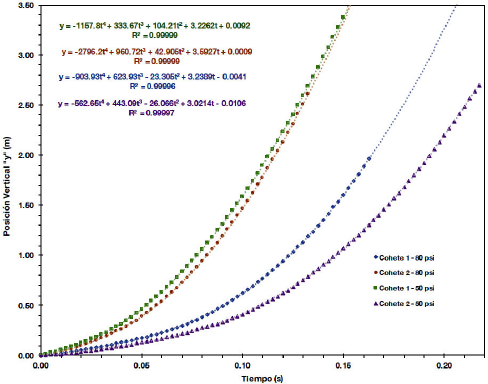
Figura 8. Posición vertical “y” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 50 psi y 80 psi.
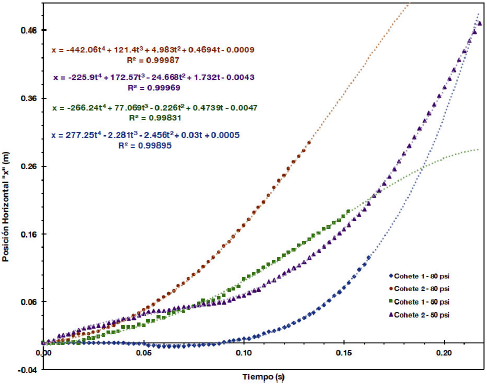
Figura 9. Posición horizontal “x” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 50 psi y 80 psi.
Tabla I. Ecuaciones de movimiento en x y y para el cohete 1 a una presión de 80 psi y con un número de datos n = 88.
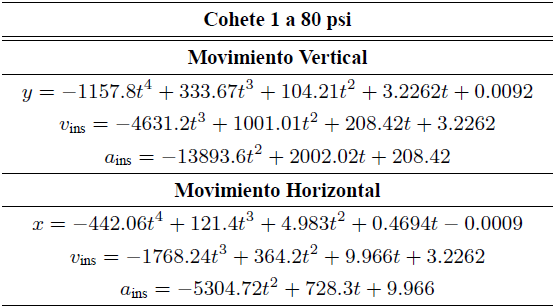
Tabla II. Ecuaciones de movimiento en x y y para el cohete 2 a una presión de 80 psi y con un número de datos n = 54.
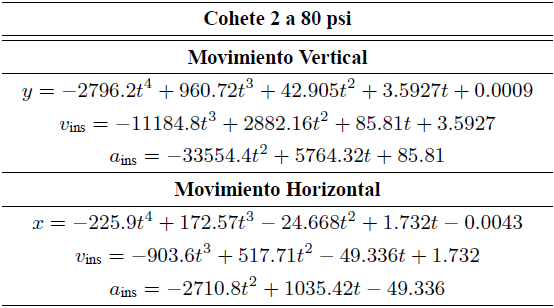
Tabla III. Ecuaciones de movimiento en x y y para el cohete 3 a una presión de 50 psi y con un número de datos n = 61.
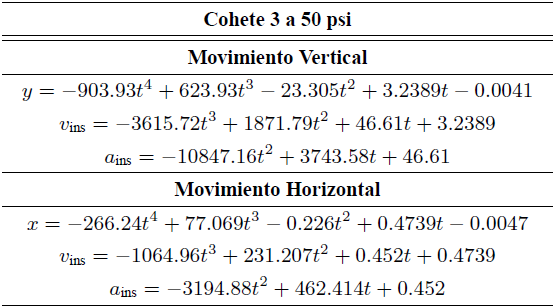
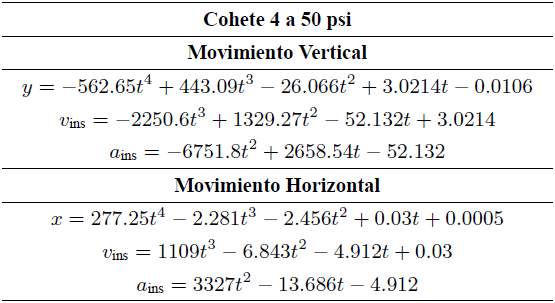
Tabla IV. Ecuaciones de movimiento en x y y para el cohete 4 a una presión de 50 psi y con un número de datos n = 88.
La velocidad promedio de cada uno de los cohetes se determina empleando el método de Euler 46 así:
donde i = 2, 3, …, n, siendo n el número total de datos de posición obtenidos para cada cohete a partir del analisis de los videos realizados con tracker.
La velocidad instantánea y velocidad promedio para cada cohete respecto a los ejes x y y se observan en las Figs. 10 y 11. De forma similar, la aceleración promedio se calcula como:
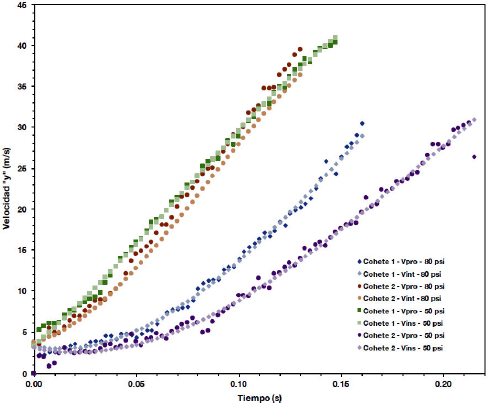
Figura 10. Velocidad promedio e instantánea vertical “y” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 80 psi y 50 psi.
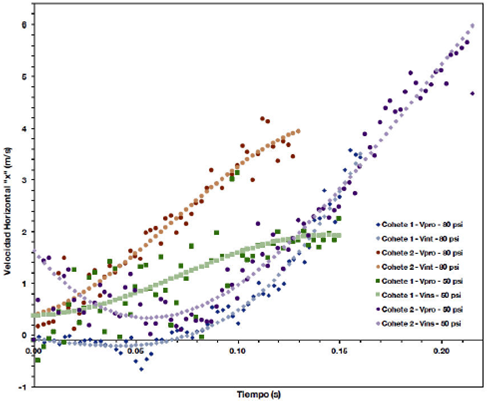
Figura 11. Velocidad promedio e instantánea horizontal “x” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 80 psi y 50 psi.
Con j = 2, 3, …, m, siendo m = n - 1 el número total de datos de velocidad obtenidos para el vuelo de cada cohete.
En las Figs. 12-15 se presenta el comportamiento de la aceleración promedio y la aceleración instantánea para cada cohete en los ejes x y y.
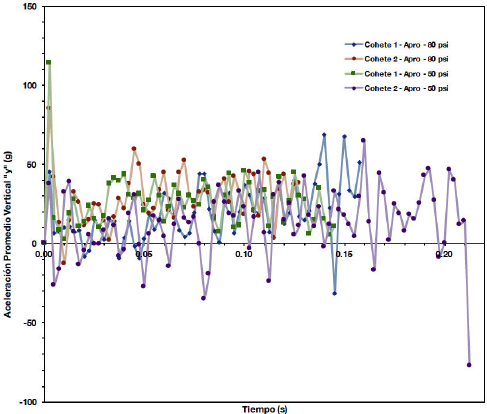
Figura 12. Aceleración promedio vertical “y” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 80 psi y 50 psi.
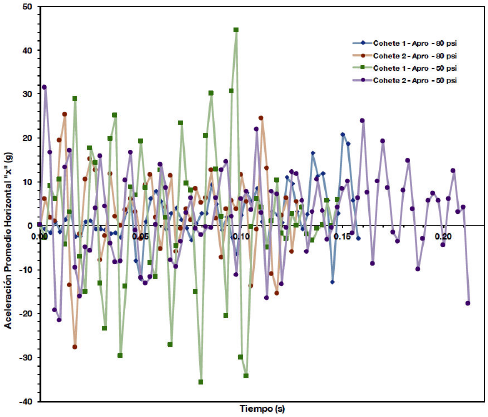
Figura 13. Aceleración promedio horizontal “x” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 80 psi y 50 psi.
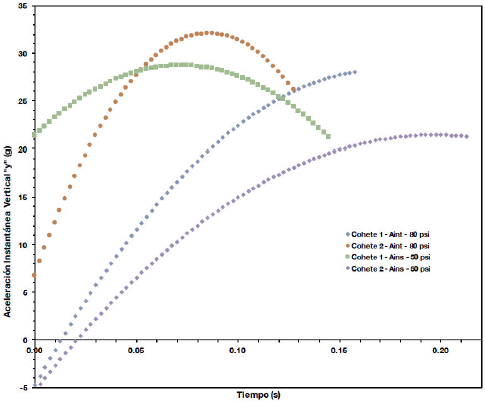
Figura 14. Aceleración instantánea vertical “y” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 80 psi y 50 psi.
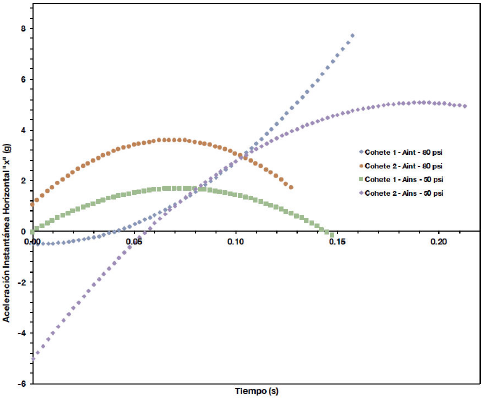
Figura 15. Aceleración instantánea horizontal “x” - tiempo, para el despegue de los cuatro cohetes hidráulicos a presiones de 80 psi y 50 psi.
Las Figs. 10 y 11 muestran que la velocidad incrementa a medida que el cohete expulsa todo su combustible líquido (agua). La aceleración instantánea obtenida por derivación del polinomio de ajuste, predice que el cohete acelera de forma continua y progresiva, mientras que la aceleración promedio obtenida por el método de Euler describe un comportamiento oscilatorio de la aceleración.
El flujo de agua expulsado por el cohete se realiza de forma continua, por lo cual la aceleración promedio obtenida por el este método no describe la realidad del sistema físico en un largo intervalo de tiempo, sin embargo, este método nos permite estudiar la aceleración promedio inicial en los primeros 2.5 ms para cada uno de los cohetes, las cuales están en el intervalo de 37.84 a 114.01 veces la aceleración de la gravedad
En la Fig. 16 del lado izquierdo se presentan los resultados obtenidos en este trabajo, para cohetes con alas, contrapeso, punta aerodinámica, de masa total sin liquido igual a 0.0823 kg, lanzados a presiones de 50 psi y 80 psi, con 0.7 litros de agua. La figura de la derecha presenta los resultados reportados por Kagan 29, para cohetes sin alas, sin contrapeso, de masa total sin liquido igual a 0.0484 kg y lanzados presiones de 50 psi y 100 psi, con 0.7 litros de agua. La discrepancia que se observa entre estos resultados radica en las distintas condiciones de lanzamiento y configuración de los cohetes. En el trabajo de Kagan, los cohetes son botellas de PET que no poseen masa de contrapeso, alas, ni punta aerodinámica, sus lanzamiento se realizaron de forma completamente vertical y con una cantidad de 0.7 litros de agua. En contraste, los cohetes empleado en nuestro experimento usan 0.7 litros de agua como combustible, si poseen un contrapeso que duplica la masa de una botella de PET vacía, tienen alas y punta aerodinámica, lo cual aumentan los efectos de la fricción, además, el hecho de que los lanzamientos no son completamente verticales no permiten al cohete lograr las mismas alturas para los mismos intervalos de tiempo.
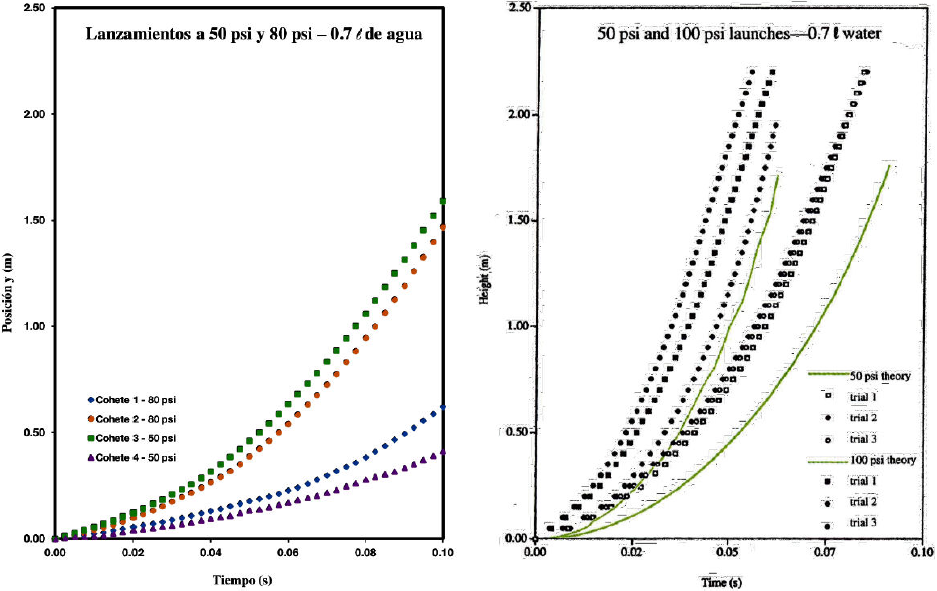
Figure 16. Posición vertical y vs tiempo, para el lanzamiento de cohetes hidráulicos. En la figura de la izquierda se presentan los resultados reportados en este trabajo. En la figura del lado derecho se presenta los resultados reportados por Kagan 29.
6. Conclusiones
El uso de una cámara fotográfica digital que graba video a 400 fps, permite obtener un máximo de 400 datos de posición por cada segundo de grabación. En este trabajo fue posible determinar la posición en función del tiempo para el vuelo de cuatro cohetes hidráulicos. A partir de estos datos, se determinan sus velocidades y aceleraciónes. En los cuatros experimentos, el número de datos mínimo y máximo obtenidos está en el rango de 54 a 88 puntos de posición y abarca una descripción que permite investigar el comportamiento físico de los cohetes hidráulicos en su primera etapa de propulsión. Un número de datos de posición como los obtenidos en este experimento garantiza una reducción en los errores adherentes al experimento y que sus efectos sean mínimos en la descrición física de estos sistemas. Se utilizó el método de mínimos cuadrados a un ajuste de un polinomio de cuarto grado y el método de Euler para determinar las velocidades y aceleraciones de cuatro cohetes hidráulicos.
La velocidad y aceleración instantáneas se obtienen a partir de la derivación del polinomio de ajuste para cada cohete. Las velocidades y aceleraciónes promedio de obtiene a través del método de Euler. Los valores de las aceleraciones promedio obtenidas por el método de Euler son fluctuantes, lo cual se debe a los errores inherentes al método mismo, ya que estas cantidades se obtienen de los valores de la velocidad promedio, lss cuales tambien fueron obtenidas por este método. En las Figs. 12 y 13 se observan estas fluctuaciones de aceleración. Físicamente, se espera que un cohete hidráulico posea aceleración, pero no fluctuante ni oscilatoria, por lo cual las Figs. 12 y 13 ofrecen un estimativo de la aceleración para ciertos intervalos de tiempo, pero con un alto grado de error. Un resultado relevante es el hecho que los cohetes al despegar presentan una alta aceleración promedio inicial, la cual está en el intervalo de 37.84
Considerar dentro del aula de clase experimentos en los cuales los sistemas presentan masa variable, ofrecen una reto educativo en la enseñanza de la física. En la gran mayoría de los libros de texto, este problema se aborda desde una perspectiva simplificada, reduciendo su descripción a un sistema con movimiento uniformemente acelerado, lo cual conceptualmente es incorrecto.
Al ser el cohete hidráulico un sistema de masa variable, los efectos en la descripción de su movimiento pueden ser perfectamente modelados a través de un polinomio de cuarto orden, en el cual se integran de forma implícita muchas características dinámica del sistema, que no son consideradas en los modelos reduccionista propuestos en los libros de texto introductorios de física.
A través del estudio de este sistema, con ayuda de tecnologías como la cámara fotográfica y videos a slow motion, el estudiante rompe un paradigma en el cual se le presentan experimentalmente unicamente sistemas con velocidades o aceleraciones constantes, pero nunca sistemas en los cuales la masa y la aceleración son variables. Con el uso de herramientas estadísticas como el método de mínimos cuadrados, es posible construir un modelo físico a partir de datos experimentales para este tipo de sistemas.
Un implementación experimental que dejamos como propuesta al lector, es sincronizar dos cámaras de video que permitan grabar el lanzamiento del cohete en dos planos perpendiculares, con lo cual se tendría información en los tres ejes espaciales y una completa descripción tridimensional del movimiento del cohete hidráulico.











 nueva página del texto (beta)
nueva página del texto (beta)