1. Introduction

One of the purposes of quantum mechanics is to find solutions for the time independent Schrödinger equation (TISE). This equation can be written as

and can be solved analytically only in a few particular cases. Undergraduate level courses focus on solving this equation for cases such as the free particle, the harmonic oscillator or the particle in a potential well. In those examples, due to the simplicity of the potential function, it is possible to find an analytical solution with a straightforward mathematical treatment. In many other much more realistic cases, the potential function is sufficiently complex to require a numerical instead analytical treatment.

The variational method is a very useful tool to compute the ground-state energy for an arbitrary system described by a complex potential function by taking advantage of the Rayleigh-Ritz variational principle ^1-3. The variational method employs a set of basis functions as trial functions, and its success relies on the selection of said trial functions. The variational method is also one of the most commonly numerical techniques to solve the TISE, therefore, in order to make the problem computer friendly, it is a good practice to study variationally the TISE using matrices.

Since numerical methods allow us to solve the TISE for arbitrary potential function, then, we can easily observe phenomena such as the tunnel effect in a potential barrier, the energy quantization of bound states and other interesting phenomena raising from periodic potential functions used to described solids.

The purpose of this paper is not only to show but also to explain an algorithm to solve the TISE in one dimension, for arbitrary, and in particular, for periodic potentials, employing the variational method and matrix mechanics at an introductory level.

We want to state that this kind of solution is already widely used in research ^4,5 and even commercial software, furthermore it is explained is scattered regions of the literature. However, we think that it is important for junior researchers to understand the power and limitations of the tools they are using. This is why this paper presents a comprehensive study of the formalism and implementation details of the variational method applied to solve the TISE and, to some extend, present some ideas of topics in computational science that can be solved with this method. We aim to encourage the undergraduate and graduate students to make a practical approach to computational quantum mechanics.

2. Formalism

Any wavefunction ψ (x) can be expanded as a superposition of energy eigenstates {ψ_n (x)} like:

where C_n is the coefficient of the ψ_n wavefunction. ψ (x) can be normalized with

It is interesting to appreciate that the space can be discretized into small intervals of size h. Therefore, if the wavefunction of a particle is described in the interval [0,a] and the space is discretized, then

The Eq. (1) can be seen as

where |ψ〉 ↔ ψ (x). The expansion (2) takes the form

Straightforward algebra induces to

where S_mn = 〈ψ_m|ψ_n 〉 is the overlap matrix and H_mn = 〈ψ_m|H^|ψ_n〉 is the component mn of the Hamiltonian matrix. To see the complete deduction, you can consult the Ref. 6. In the matrix way, the problem reduces to a generalized eigenvalue problem ⁷

where C_n is the eigenvector associated to the eigenvalue E_n, and the wavefunction for the state n is found from the trials functions and the coefficients C by

If the set of basis |ψ_n〉 is orthonormal, the element 〈ψ_m|ψ_n〉 is equal to the Kronecker delta, δ_nm, and the matrix S becomes the identity. Then the problem is reduced to a symmetric eigenvalue problem ⁸. If the bases are not normalized (〈ψ_n|ψ_n〉 6= 1), the elements H_mn and S_mn should be preciously divided by the inner product 〈ψ_m |ψ_n〉 to guarantee the normalized eigenstates.

In order to construct the Hamiltonian matrix, it is necessary evaluate the kinetic and potential energy matrices by means of

where T^ is the kinetic energy operator defined in reduced units (ℏ = m = 1), in one dimension, as

And V^ is the potential energy operator. So, the elements T_mn and V_mn are found using the following equations

Therefore, the value of H_mn can be evaluated by

At this point, we could solve the TISE for a potential function even thought the mathematical treatment for the differential equation is unfeasible. In such cases, the problem can be solved by means of variational method. The process starts by proposing a set of basis functions. In order to comply with the computational constraints the number of functions in this set have to be some how small. However, the accuracy of the solution grows with the number functions of the basis set. F. Marsiglio ⁴ solved the TISE through the variational method, using the solutions to the infinite potential well as elements of the basis set

where a the potential well width. He computed analytically the elements H_mn for the harmonic oscillator and various square wells. However, it is not always possible to evaluate the integrals (13) and (14). When this happens, numerical integration methods can be applied to come up with the H_mn matrix elements.

After obtaining the elements H_mn, and in some cases S_mn, it is possible to solve the generalized eigenvalue problem (8), which can be reduced to a diagonalization problem, as mentioned in ⁷.

In general, the aforementioned numerical integration methods require to narrow and apply discretization to the integration range, thus, in general, it is impossible to integrate over all space. A smart solution for that is to assume that the particle is enclosed in an infinite potential well, thus the potential function, that describes the system, lays between two infinite potential barriers. The position of said barriers can be used as limits for the integrals (13) and (14). This also ensures that all states are bounded. Some of these states are bounded to the original potential function and the rest are bounded to the combination of the infinite potential well and the original potential. The latter states are not useful for us, because they deviate from the solution of our initial problem. However, the amount of states bounded to the original potential function increases with the width of the infinite potential well. Furthermore, a good choice for the functions in the basis set is to choose them so that they should be able to form a root (zero amplitude) in both walls of the potential well.

The dispersion relation (E (K)) is a very important property of a material ⁹, and also, it is very useful in solid state physics. In a typical solid, the allowed energy bands are separated by band gaps, or forbidden energy bands. Such configurations along with the Fermi energy, define if a material is conductor, insulator or semiconductor. There are several models, which have analytical solutions, that reproduce these phenomena. One of the most studied examples is the one dimensional Kronig-Penney model. Such one dimensional solutions give an idea about the physics of quantum systems and serve as an overview of these phenomena in three dimensions.

The periodic potentials feature energy bands in their dispersion relations. To solve the TISE for a periodic potential using the variational method, a smart choice is to pick a set of periodic functions to conform the basis set. The trick of embedding the potential into the infinite potential well will not be necessary in these cases. R. L. Pavelich et al. ⁵ studied the Kronig-Penney model and arbitrary periodic potential by means of variational method employing one dimensional plane-wave basis set, which are defined as

where a should be a multiple of the period of the functions that we want to reproduce and K_n the wave number. However, they also computed analytically the elements H_mn too, so the possible potentials are special, in the sense, that the mathematical treatment is feasible. The allowed values for K_n are 2πn/a in order to keep the periodic boundary conditions. The plane-wave basis set is a good choice because it is closely related to Fourier expansions, thus, it might be able to reproduce any periodic function of periodicity a.

Imagine a metal that exhibits a crystalline structure. Such metal can be seen as an one dimensional lattice, where the ions are arranged in such a way that there is a periodicity a. Those ions can be modeled with a potential function of periodicity a such that

Therefore, the potential energy operator is invariant under displacements by α. The kinetic energy operator also remains invariant under the aforesaid displacements, because the second derivative operator keeps the periodicity of the functions it operates on. This implies that solutions to the TISE can be expressed in terms of the solution for a unit cell only corrected by a phase factor, thus

where K is the Bloch vector which, in our case, is a number because we are working in one dimension. All K values that differ by a multiple of 2π/a are equivalent due to phase factor periodicity. Therefore, the values for K can be restricted in the interval −π/a ≤ K ≤ π/a and refolded by means of a translation by 2πn/a, K → K + 2πn/a, where n is an integer. K is continuous because the potentials are repeated indefinitely. In this way, there is a solution for each K.

The Bloch’s theorem establish that ψ_K,n can be written as a product of a periodic function u_n of period α and a planewave function. That is

Thanks to Bloch’s theorem (19), it is only necessary to solve the TISE within a single unit cell (0 ≤ x ≤ a), for several values of K between −π/a and π/a, in order to generate the solution for any region ^1,10. Then, we only need to propose a basis set to described u_n.

3. Algorithm

To solve the TISE by means of the variational method, is to choose a set of basis. For non-periodic potential functions, we assumed that the particle is bound to an infinite potential well of width a. For periodic potential functions, there is a periodicity and the problem is reduced to an interval [0,a]. In order to use computational differentiation and integration methods, this range is divided into sub-intervals of size h.

In order to find the element T_mn, we can change the limits of (13)

Using the finite differences method, the second derivative of a basis function will be ¹¹

where h is the distance between two consecutive points, x_i and x_i+1. In order to compute the second derivative at x = 0 and x = a, we employ the finite differences method forward and backward respectively, then

and

We use the composite Simpson’s rule to calculate the definite integrals required to evaluate both T_mn and V_mn. This method can be summarized as

Because the discretization of the range, the functions can be seen as numerical arrays

and the integrands become

Then, the integration is computed by means of (25) as

where f can be the integrand for T_mn or V_mn.

At this point, the matrix H_mn is known. The next step is to determine C_n and E_n in the eigenvalue problem (8). If the basis set is orthonormal, and therefore, the overlap matrix S is the identity matrix, then, the problem is solved directly. Otherwise, it is necessary to find a transformation to turn the problem into a symmetric eigenvalue problem. The Givens-Householder QP decomposition is a known procedure to make that happen ^6,7. Using this method, the overlap matrix S should be transformed into an unit matrix by means of a matrix V such that

The extend explication can be consulted in ⁷. It is advisable to use a numerical library to compute the eigenvalues and eigenvectors of both H and S because the programming is difficult and confusing. We use scipy’s linal.eig function ¹², which solves an ordinary or generalized eigenvalue problem of a square matrix using routines from LAPACK. The aforementioned routine takes in as arguments the matrix H and optionally the overlaping matrix S, in case of a generalized eigenvalue problem, and returns a vector E with the eigenenergies and a matrix C with the eigenvectors. The eigenvector matrix C is layed out in such a way that its nth is the eigenvector corresponding to the nth element in the eigenenergy vector E. However, any another routine can be used to solve the eigenvalue problem.

At this point, we know both E_n and C_n. Therefore, we can compute the wavefunction for the state n, using the elements of the previously calculated matrix C as coefficients of the basis functions, by means of (9) and, from this, the probability density function ρ can be evaluated

If the potential is periodic, the above steps are followed using a periodic basis set, like the plane-waves (20), repeating the process for several values of K and calculating the values for E_n as a function of K to get the band structure, which is the uttermost property of periodic potentials.

4. Non-periodic potential examples

The algorithm explained in Sec. 3. is used to compute the eigenenergies and probability densities for the harmonic oscillator potential and the barrier potential, both embedded in the infinite square well

For the harmonic oscillator potential, it is possible to compare both the eigenenergies and the eigenvectors with the theoretical values available in standard quantum mechanics books.

4.1. Harmonic oscillator potential

The form of the harmonic oscillator potential is

Vx=12mω2x-a220<x<a (33)

where m is the particle mass, ω is the angular frequency related to the particle and, in this case, the potential is centered around a/2. The analytical solution of (1) for this potential function is ¹

En=n+12ℏω  n=0,1,2,… (34)

for eigenenergies and

ψnx=mωπℏ1/412nn!exp-mωℏx-a22×𝓗nmωℏx-a2 (35)

for eigenvectors, where H_n are the Hermite polynomials defined

𝓗nx=-1nexpx2dndxnexp-x2 (36)

We picked two different basis sets. The infinite square well solutions (16) were chosen as basis set 1. Another basis set with the form

ψn=xx-asinnπxa (37)

was chosen as basis set 2, which is neither normalized nor orthogonal. For this reason, the basis set 2 must be normalized before solving the generalized eigenvalue problem. The well width was set at a = 1.0 and the angular frequency at ω = 50. The number of divisions was set at 10000 such that h is 0.0001.

The number of basis N was set at 30, for both basis set, yielded a good approximation while keeping a reasonable run time.

Figure (1) shows a plot of the probability density function for the ground state and the first three excited states in the harmonic oscillator potential, comparing them with the analytical solutions.

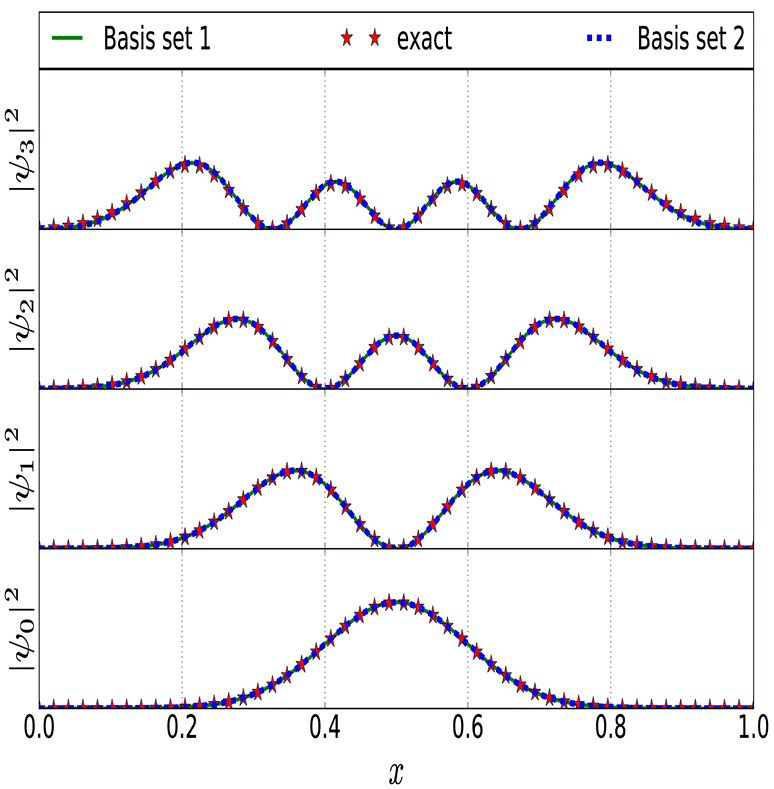
Figure 1 Probability density function |ψ_n|² for different energy levels n for the harmonic oscillator potential. The probability densities for the basis set 1 and 2 overlap, that is why only one function shows up in the figure (color online). 

Table I shows the eigenenergy values obtained by the variational method both basis set and comparing them with the theoretical values from (34). Results show that the error increases when n increases, which is expected because the variational method guarantees an accurate solution only for the ground state (n = 0). However, the basis set 1 is a better choice that basis set 2 because it can reproduce accurately the exact solution. This was expected because the basis set 1, being solution to the infinite well potential, can adjust easily to any function embedded in this potential. However, the basis set 2 returns a good approximation because it presents nodes in the walls and has behavior similar as the basis set 1. The error for the ground state with the basis set 1 is around 0.004%. When the state’s energy reaches the maximum value of potential, then the states stop belonging to harmonic oscillator potential and become close to the solutions for a particle confined in an infinite square well with a harmonic oscillator potential. This can be readily observed in the Table I and in the Fig. 2. The maximum value of the potential, when ω = 50, is 312.5 and the energy for states n = 6 and n = 7 exceeds that limit thus the error for those levels is notably larger than the error for lower values of n.

Table I Eigenenergy values for the harmonic oscillator. 

n	En (Basis 1)	En (Basis 2)	En theoretical	%ε (Basis 1)	%ε (Basis 2)
0	25.001	25.001	25.0	0.004	0.004
1	75.016	75.022	75.0	0.021	0.029
2	125.164	125.208	125.0	0.131	0.1664
3	175.989	176.203	175.0	0.565	0.687
4	228.973	229.721	225.0	1.766	2.098
5	286.558	288.232	275.0	4.203	4.812
6	351.277	354.566	325.0	8.086	9.097
7	424.839	429.873	375.0	13.290	14.633

Figure 2 Schematic representation of the harmonic oscillator potential “embedded” in an infinite square well of width a = 1, for the basis set 1. 

In order to reach more energy levels, the width a should be increased, so that the maximum value of potential increases accordingly. This requires to increase the number of divisions and the number of functions in the basis set to preserve the accuracy. Accordingly, the width of the well was increased to 1.5 and to preserve the value for the size interval h, the amount of divisions was increased to 15000. Figure 3 shows that, as it was expected, the eigenenergies are accurate even for the state n = 10, above which the method begins to fail.

Figure 3 Schematic representation of the harmonic oscillator potential “embedded” in an infinite square well of width a = 1.5, for the basis set 1. 

4.2. Rectangular potential barrier

The rectangular potential barrier function is one of the simplest potentials that is employed for educational reasons to illustrate some non-classical effects like quantum tunneling. This phenomenon occurs when a particle travels towards a barrier potential and there is a probability for the particle to cross the barrier, even if the energy of the particle is lower than the height of the barrier. The barrier potential has the form

Vx=V0Θx-dlΘx+dr0≤x≤a (38)

where Θ is the Heaviside step function, V₀ is the barrier height and d_l and d_r are the position for the left and right walls, respectively, such that the barrier center is in d_l + d_r/2 with a width of d_r − d_l, being d_r> d_l.

To solve this potential, the trick aforementioned in Sec. 3 is used again. Therefore, the potential barrier is embedded in an infinite potential well. This problem can be solved analytically and compared with the numerical solution. The scheme for this problem can be visualized in the Fig. 4. The mathematician treatment is feasible for this case, which is useful to compare with the numerical solutions. You can consult the Appendix for the deduction. To compute the allowed energies (bound energies), it is necessary to solve the transcendental equation arising from the mathematician deduction

exp⁡(-4αb)[α-κcot⁡(κ(a2-b))]2=[α+κcot⁡(κ(a2-b))]2 (39)

where α=2mVo-E/ℏ and κ=2mE/ℏ. A good technique to solve the above equation is the graphical method, which consists in plotting the left and right sides of the Eq. (39) as a function of κ. The crosspoints of the two functions return the allowed values for κ and, subsequently, the allowed values for E. Figure 5a shows the graphical solution for V_o = 50, a = 1.0 and b = 0.1. For this specific case, there are two bound states; hence, there must be two intercepts. The two values for κ were 5.81325 and 6.58358, which correspond to values for the energy E of 16.897 and 21.672, respectively. For applying the variational method, the interval size h was set at 0.0001 and the amount of basis N was set at 30. Figure 5b shows the two levels of interest, with energies 16.899 and 21.673. The relative errors for those levels are 0.012% and 0.005% respectively, which implies that the variational method is very accurate to the analytical solution.

Figure 4 Schema of the rectangular potential barrier embedded in an infinite potential well. 

Figure 5 Analytical solution (a) and variational solution (b) for the potential barrier embedded in an infinite potential well with reduced units (~ = m = 1), V₀ = 50, b = 0.1 and a = 1.0. The graphical method is employed for the analytical solution (39). 

On the other hand, if the barrier is centered at a/2 and the barrier height is huge, the energy levels becomes two-folded degenerate, because there is some kind of arbitrariness due to symmetry, and the energy is the same when the particle travels from left to right or from right to left. Figure 6 shows the first four states for the potential mentioned above and it is possible to visualize that the wavefunctions for the states n = 0 and n = 1 are different although their energies are the same. Same happens for the state n = 2 and n = 3. This is an evidence that the levels for the bound energies are twofolded degenerated. The last simulations were carried out for V_o = 1000, a = 1.0 and b = 0.1.

Figure 6 Different states of the potential barrier showing degeneration. The scheme for the potential is a guide to the eye. 

Similar results were finding by V. Jelic et al. ¹³ for a double-well potential embedded in an infinite potential well, where again appears the degeneracy as a result of symmetry and a barrier height sufficiently large.

Other important phenomenon is the quantum tunneling, which is possible to visualize if the probability density function in the opposite side of the potential is greater than zero. In this case, we simulate an asymmetric potential barrier, recurring to Eq. (38), and set d_l = 0.5, d_r = 0.6, a = 1.0 and V₀ = 500. Figure 7 shows that in the right side the probability density function is greater than zero. For this case, it is thought that the particle travels from left to right and it crosses the barrier allowing appreciate the tunnel effect, although the particle energy (E₇ = 275.980) is lower that the barrier height.

Figure 7 Probability density function for the state n = 7 for a particle in an asymmetric potential barrier embedded in the infinite potential well. 

This problem could be more realistic in the nature, because the particles in the devices are thought as confined and can be seen like a infinite potential well.

5. Periodic potentials

Besides, the algorithm explained in Sec. 3. is also used to compute the energy bands for the Kronig-Penney model and for a more realistic potential, named “pseudo-Coulomb” potential.

5.1. Kronig-Penney model

The Kronig-Penney model consists in an infinite periodic array of rectangular potential barrier functions. This model illustrates a perfect one dimensional crystal and its solutions resemble important features of the quantum behavior of electrons in periodic lattices ¹¹.

The potential of the Kronig-Penney model has the form for a unit cell, where a is the unit cell width, b < a and V₀ are the potential barrier width and height, respectively. Figure 8 shows a scheme of the Kronig-Penney model’s potential.

V0<x<a=00<x<a-b2V0a-b2≤x≤a+b20a+b2<x<a (40)

Figure 8 Kronig-Penney model. 

The analytical solution is studied in detail in Ref. 14. The final expression for the dispersion relation is

cosKa=-α2+β22αβsinαa-bsinβb+cosαa-bcosβb (41)

where α=2mE/ℏ and β=2mE-V0/ℏ. This relation will be useful to estimate the error in the numerical solution.

In order to solve the TISE for this potential, the planewave basis set was chosen. Therefore, the values for K are varied from −π/a to π/a. This interval was divided at 100 equal parts, and for any part, the algorithm explained in 3. is used to find a set of energies for each value of K. This set of energies returns the dispersion relation. Besides, the amount of basis N was set to 15 that corresponds to 31 plane-waves because n, for this case, runs from −N to N including zero. Moreover, the interval from 0 to a was divided into 10000 parts. These quantities were fixed to ensure an accurate solution. For the simulation, the unit cell width a is set to 1.0, the barrier width b is varied and the barrier height V₀ is fixed to 50. Again, the constants are reduced, so that ℏ = 1 and m = 1.

Figure 9 shows the numerical (solid lines) and analytical solutions (squares) for different values of b. The potential barriers (vertical textured regions) are plotted to improve the visualization. The horizontal shaded regions are known as band gaps or forbidden energy bands, since it is not possible for the particle to have energies in those regions. As the potential barrier b increases, the band gaps width also increase, up until b arrives to 0.5a, where the band gaps width starts decreasing as the potential barrier b increases. That is because for b = 0.0a, the model reduces to the free particle model, similarly for b = 1.0a, the model reduces to the free particle model plus a constant and uniform potential or gauge.

Figure 9 Numerical solutions to the dispersion relation for the Kronig-Penney model, for b = 0.0a, 0.25a, 0.5a, 0.75a and a, respectively. 

5.2. Pseudo-Coulomb potential

The pseudo-Coulomb potential, or soft-Coulomb potential, is a more realistic model for electrons traveling through periodic lattices, where the interaction between the electrons and the ions in the lattice is approximated to the Coulomb potential between charged particles. This potential can be written as

Vx=Keq1q2x-a2 (42)

where K_e is the Coulomb’s constant and q₁ and q₂ are the particles charges. The potential is centered around a/2. However, the potential diverges when x = a/2. In order to avoid such divergence, a softening parameter b is added, and Eq. (42) takes the form

Vx=Ab-Ax-a22+b2 (43)

where A is a positive number that represents the product K_eq₁q₂ and it is called strength, and b is a positive and small softening parameter introduced to prevent singularities ⁵. We introduce the potential gauge A/b to keep the potential values greater than zero.

The pseudo-Coulomb potential falls into the category of interesting and realistic potentials where the mathematical treatment is so hard that, until now, it has been impossible to arrive to an analytical solution. The pseudo-Coulomb potential has been used to study auto-ionized states ¹⁵.

Again, the plane-wave basis set is chosen for this potential. The values were fixed at A = 50, b = 0.3a and a = 1.0. Figure 10 shows the numerical solution for the relation dispersion in this potential. The thick line represents the potential for visualization issues, while the thin lines, the dispersion relation (E (K)). The dispersion relation for pseudoCoulomb potential also features band gaps, (shaded regions in the plot), as expected for periodic potentials.

Figure 10 Numerical solution to the dispersion relation for the pseudo-Coulomb potential, with A = 50 and b = 0.3a. 

6. Summary

The intended audience of this work are students starting in the field of computational quantum mechanics. We explain a sequence of steps to solve the stationary Schrödinger equation for arbitrary potentials, which can be non-periodic or periodic. For the periodic potentials employing the Bloch’s theorem. Moreover, we explain the fundamentals of the variational method and matrix mechanics. A student, with the help of this paper, should be able for implementing a code to solve the TISE, in his preferred programming language. However, the results and plots were obtained with a program implemented in python3 and can be consulted in the link https://gitlab.com/jdalzatec/TISE. The graphical interface was implemented by means of PYTHON-GTK. Although this paper is geared in a basic way, the student has the freedom to practice with any other potential function, using his program or ours, and compares his results with theoretical ones, whenever is possible to get an analytical solution.