PACS: 42.81.-i; 41.20.Jb; 42.25.Gy; 02.70.Bf
1. Introducción
Existen diferentes fenómenos ópticos que ocurren a frecuencias imperceptibles a la vista humana, por lo que se requiere mayor exactitud y comprensión de los mismos, las herramientas del electromagnetismo computacional sirven para poder modelar estos fenómenos. En el presente trabajo se utiliza el Método de Diferencias Finitas en el Dominio del Tiempo (FDTD) para resolver las ecuaciones de Maxwell y para analizar el comportamiento de los campos electromagnéticos en el interior de una fibra óptica.
Para entender la comunicación por este medio se considera la luz como una onda electromagnética de la misma naturaleza que las ondas de radio, con la diferencia de que la longitud de onda se considera del orden de micrómetros en lugar de metros, como se usa en comunicaciones de radio 1.
La fibra óptica está compuesta de un material dieléctrico consistente en un núcleo y el revestimiento, que mediante la reflexión interna total, permite la propagación a lo largo y en el interior de la fibra. El núcleo, que es la parte interna de la fibra propaga la luz de un extremo a otro, es fabricado de silicio o de cuarzo fundido dopado con otro material, su diámetro se encuentra en el rango de micras 2. La propagación de la señal en el interior de la fibra se logra cuando el índice de reflexión n1 del núcleo es mayor que el índice de refracción n2 del revestimiento.
En el presente trabajo se muestra el comportamiento multimodal al propagarse la señal por distintos modos o caminos para llegar al otro extremo de la fibra óptica; se presentan también los cálculos para el requerimiento de cómputo mínimo que se necesita para la implementación del método FDTD, el cual se logra mediante la implementación de una región de cálculo formada por celdas cuadradas, con tamaño de 80 nm en cada uno de sus lados, se consideran 62500 celdas para el eje X y 62500 celdas para el eje Y, obteniendo un mallado total de 3 906 250 000 celdas.
Haciendo un poco de historia, es importante señalar que hubo una intensa discusión acerca de la naturaleza de la luz entre los seguidores de Descartes y de Newton que en la actualidad es poco recordada. El debate posterior entre los seguidores de Newton y de Huygens notablemente opaca al primero en interés científico e histórico. Brevemente, en el primero se cuestionaba si la luz es un fluido compuesto por minúsculos torbellinos o si está formada por partículas, esta era una discusión con un alto contenido especulativo en donde argumentos físicos, metafísicos y teológicos frecuentemente se mezclaban complicando enormemente el razonamiento 3.
Los científicos de aquella época aceptaron la teoría corpuscular de la luz de Newton. Sin embargo, en 1678 Christian Huygens, demostró que la teoría ondulatoria de la luz podía explicar también los fenómenos de reflexión y refracción que se mostraron con la teoría corpuscular, sin embargo, la teoría ondulatoria no fue aceptada de inmediato. Asimismo se argumentaba que si la luz era alguna forma de onda, debería rodear obstáculos; este fenómeno es conocido como difracción. Francesco Grimaldi proporcionó pruebas experimentales para la difracción, pero fue hasta 1801 cuando Thomas Young, demostró que en condiciones apropiadas, los rayos luminosos interfieren entre sí. Agustín Fresnel, realizó varios experimentos relacionados con la interferencia y la difracción y en 1850 Jean Foucault demostró que la rapidez de la luz en líquidos es menor que en el aire, cabe mencionar que de acuerdo con el modelo corpuscular, la rapidez de la luz sería más alta en líquidos que en el aire 4.
Poco a poco la teoría ondulatoria fue cobrando credibilidad, en 1873 Maxwell, afirmó que la luz era una forma de onda electromagnética de alta frecuencia, Hertz proporcionó la confirmación experimental de la teoría de Maxwell en 1887 al producir y detectar ondas electromagnéticas, Hertz y otros investigadores demostraron que estas ondas experimentaban reflexión y refracción y presentaban todas las otras propiedades características de las ondas.
Aunque el modelo ondulatorio y la teoría clásica de electromagnetismo pudieron explicar la mayor parte de las propiedades conocidas de la luz, el efecto fotoeléctrico, descubierto también por Hertz, expone que cuando la luz incide sobre una superficie metálica, algunas veces los electrones son arrancados de la superficie. Una explicación del efecto fotoeléctrico fue propuesta por Einstein en 1905 en una teoría que empleó el concepto de cuantización desarrollado por Max Plank en 1900.
Los fenómenos implícitos en la propagación electromagnética son un tanto difíciles de explicar desde el punto de vista didáctico, por lo que en este artículo se presenta el modelado de una fibra óptica de índice escalonado y se aprecia la propagación multimodal, con la finalidad de que los estudiantes puedan comprender mucho mejor lo concerniente a este tipo de propagación.
2. Método de Diferencias Finitas en el Dominio del Tiempo
La implementación del método de Diferencias Finitas en el Dominio del Tiempo (FDTD) transforma las ecuaciones de Maxwell en forma diferencial a ecuaciones de diferencia finita, para este caso, se estudia un sistema en modo transversal eléctrico (TE) bidimensional.
En la Ec. (1) se determina la componente de campo eléctrico Ez y en las Ecs. (2) y (3) las componentes de campo magnético Hy y Hx respectivamente, correspondientes a las ecuaciones de Maxwell expresadas en diferencias finitas 5.
Donde Ez (V/m) es la componente de Campo Eléctrico en el eje Z, Hx y Hy representan las componentes de campo magnético (A/m) en el eje X y en el eje Y respectivamente, μ es la permeabilidad del espacio libre (H/m), ϵ es la permitividad del espacio libre (F/m), σ es la conductividad eléctrica (S/m) y σ* es la pérdida magnética.
3. Método de Capas Perfectamente Acopladas (PML)
Existen varias técnicas para la implementación de las condiciones de frontera de absorción en el método FDTD, como son: el esquema de diferencias finitas de Taflove 6, el modelo propuesto por Mur 7, el modelo de Capas Perfectamente Acopladas (PML) de Berenger 8, el PML en su versión reducida propuesto por Benavides 9, éste último es el utilizado en el este trabajo por presentar menor reflexión en la periferia de la región de cálculo.
La condición de frontera de absorción de Capas Perfectamente Acopladas (PML), es la condición de frontera absorbente más empleada por su versatilidad y su eficiencia, es una técnica optimizada para la implementación del modelo mediante un conjunto reducido de ecuaciones. La formulación del método PML, está basada en la representación física del medio, lo que se logra mediante sus características eléctricas y magnéticas.
Las ventajas de utilizar la técnica propuesta PML se resumen a continuación:
Para representar toda la región de cálculo, se requiere solamente un conjunto de doce ecuaciones en el caso tridimensional, mientras que en el caso bidimensional sólo se requiere un conjunto de cuatro ecuaciones.
Se facilita una transición natural de la región de análisis a la región PML, ya que no es necesario utilizar condiciones de conexión en la interfaz de la región de interés con la región PML.
Es posible utilizar un perfil de conductividad polinomial o geométrico que mejora la capacidad de absorción de la capa PML.
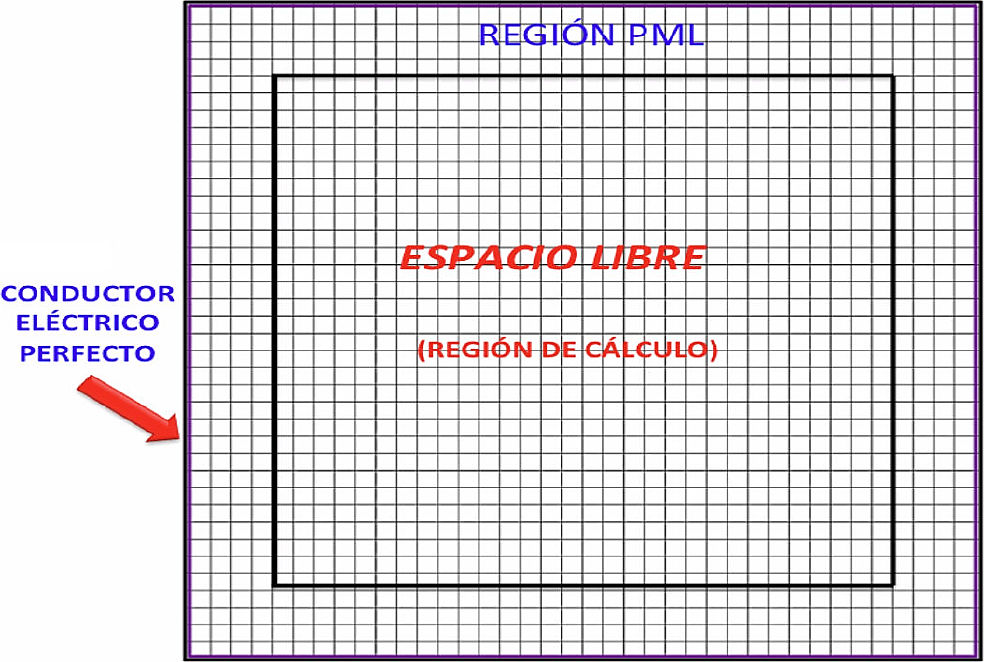
En la Fig. 1 se muestra las regiones para el PML: a) el espacio libre o vacío, b) la región PML o medio absorbente, modelando la periferia de la región de cálculo con un conductor eléctrico perfecto.
Los medios para el método PML son definidos detalladamente en 10, mediante un conjunto de ecuaciones en las que las conductividades (σ) y las pérdidas magnéticas (σ*) son relacionadas tal y como se muestran en la Tabla I.
Para la correcta implementación del Conductor Eléctrico Perfecto (PEC), se debe cumplir con las condiciones correspondientes a su comportamiento al incidir una onda electromagnética sobre él. Si bien es cierto que la región absorbente forma una región de atenuación de la señal, hasta que es prácticamente absorbida, el PEC permite truncar la propagación de la señal hacia el exterior de la región de cálculo y debe cumplir con las condiciones de frontera de espesor nulo, así como que los campos eléctricos tangenciales y los campos magnéticos normales a su superficie deben ser igual a cero 11.
Para la implementación de las ecuaciones, se considera un artificio matemático propio del método PML 12, en donde la componente de campo eléctrico Ez = Ezx + Ezy, cabe señalar que no debe confundirse con la descomposición en componentes físicas; es decir, es sólo una conveniencia matemática y parte del método 12, por lo que se sustituye en las Ecs. (1) a (3), quedando el conjunto de Ecs. (4) a (7) expresadas en diferencias finitas, tal como se indica a continuación:
4. Fuente de Excitación
El algoritmo FDTD es la solución a un problema de valor inicial y requiere un esquema de excitación para iniciar la simulación. La región de cálculo se divide en dos secciones, la región de campo total y la región de cálculo reflejado. El plano incidente es la separación de estos dos planos, en la región de campo total se considera la onda incidente y la onda dispersa; en la región de campo reflejado solo hay reflexión desde la región de campo total. Debido a que no existen discontinuidades en ésta región estas señales no se reflejarán de nuevo hacia la región del campo total. Ahora bien, éste método puede generar la propagación de ondas parásitas o espurias, que son señales indeseables que pueden afectar la precisión de la solución 12.
Para reducir el número de ondas parásitas al usar el método FDTD se consideró que las componentes de campo eléctrico y magnético variarán en el espacio temporal (superíndice de las componentes de las Ecs. (1) a (7)) y en el espacial (subíndice de las componentes de las Ecs. (1) a (7)), programándolos en el código computacional. La resta del campo incidente al plano incidente es necesario para reducir la suma de ondas parásitas o espurias en el comportamiento del esquema FDTD.
donde, Is y Js son las coordenadas en donde se localiza la fuente de excitación, frad es la frecuencia central de operación en radianes, dt es el escalón temporal y n es el numero de iteraciones.
5. Modelado de la Fibra óptica
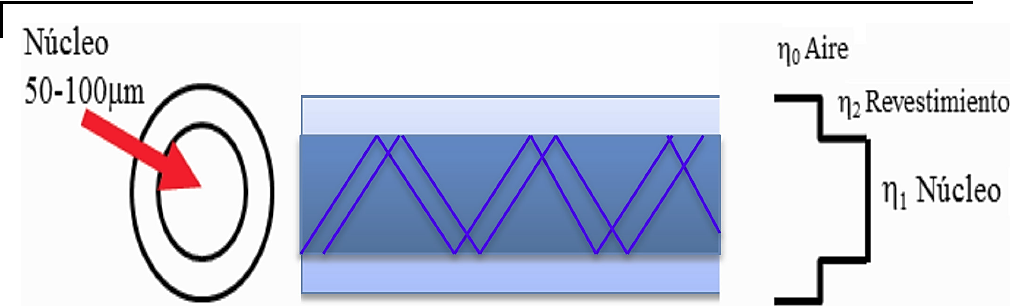
Se analiza una fibra óptica de índice escalonado, en la Fig. 2 se representa una fibra con el núcleo y un recubrimiento solamente.
Para simular la fibra óptica multimodal, se realizó un algoritmo en el software Matlab, utilizándose también éste como interfaz gráfica. Se considera que:
Donde c es la velocidad de la luz en el espacio libre (m/s), λ es la Longitud de onda (m) y f es la frecuencia (Hz).
Si λ = 1600 nm, entonces:
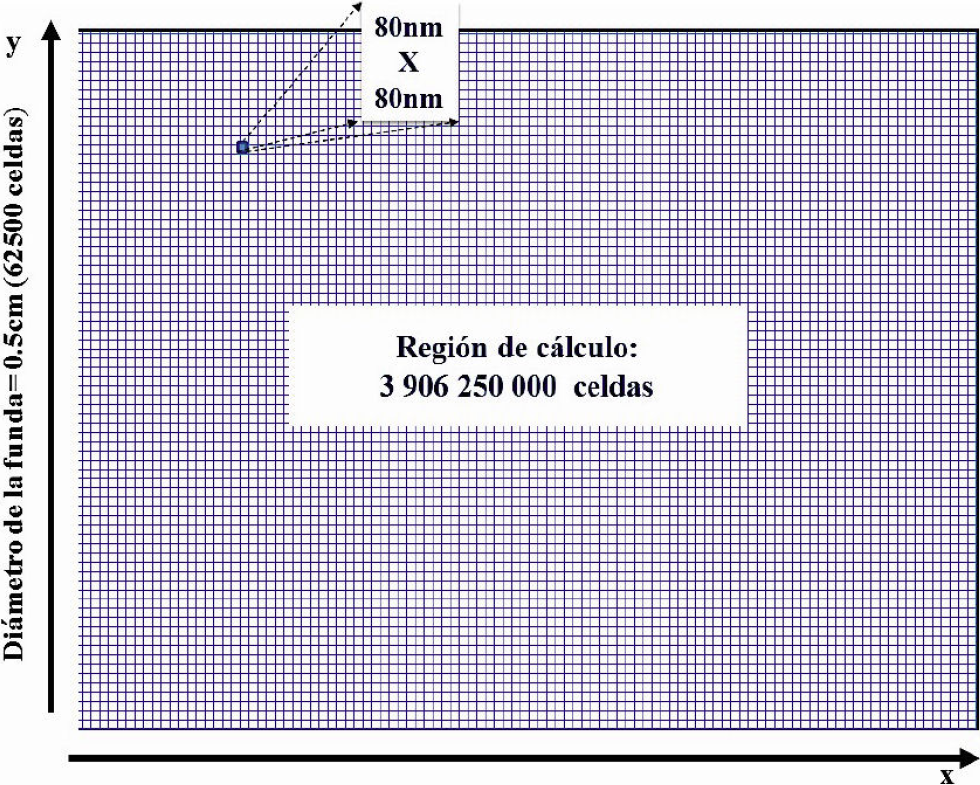
Una vez conocida la frecuencia, se calcula el tamaño de la celda de la región de cálculo (Δ) , entre mayor sea el número de celdas aumenta el recurso de memoria computacional para llevar a cabo la serie de cálculos; en este caso se considera 20 celdas por cada longitud de onda, tal y como se muestra en la Fig. 3, de acuerdo a la Ec. (12):
El índice escalonado de una fibra óptica 14, significa que se establecen diferentes valores de capas o revestimientos al núcleo de la fibra óptica hasta llegar a la funda. Estos recubrimientos tienen valores de índices de refracción diferentes para que la onda se vaya atenuando.
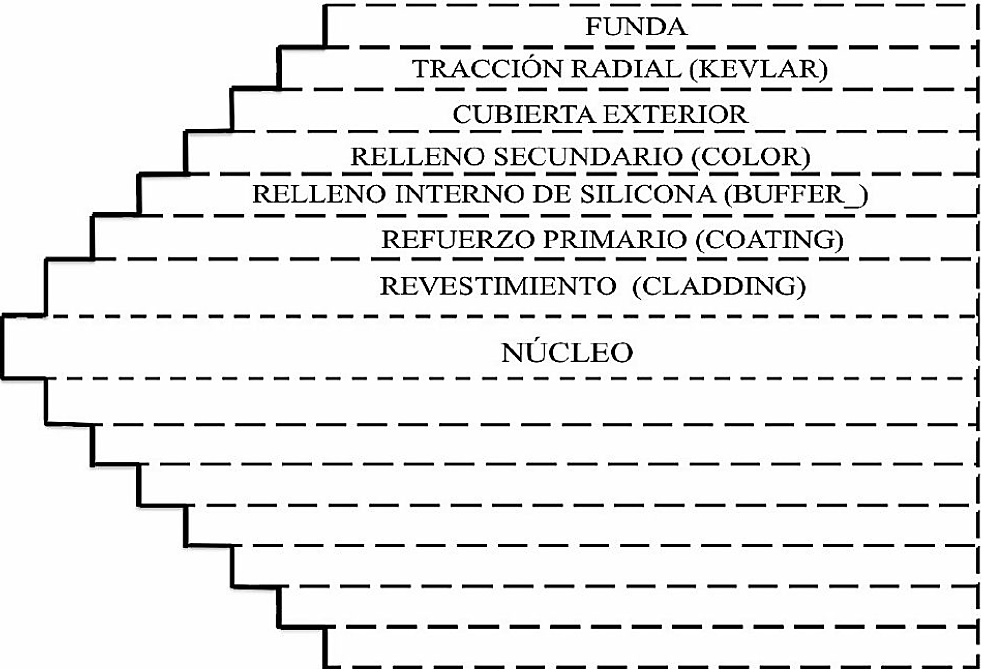
Se modelan los revestimientos alrededor del núcleo, cada uno de ellos con diferentes índices de refracción, de allí el nombre de fibra óptica de índice escalonado. En la Fig. 4 se puede observar el número de celdas que ocupa el núcleo y cada uno de los revestimientos de la fibra óptica, así también se presenta los valores en número de celdas en donde se ubican el núcleo y los revestimientos dentro de la región de cálculo que se implementó.
En la Tabla II se muestran los índices de refracción tanto del núcleo como de cada una de las siete capas que conforman la fibra óptica. Se muestra a detalle el nombre de cada capa y el material del que está fabricado.
Cabe mencionar que las dimensiones de la fibra óptica a simular es en base a la norma: Fibra multimodo 62.5/125 EIA-492: ISO/IEC 793. A continuación se muestran los cálculos necesarios para el núcleo y para cada uno de los revestimientos 13.
6. Requerimientos de cómputo del sistema
Para poder realizar la simulación de forma exitosa, se debe garantizar los recursos de cómputo necesarios para los requerimientos del algoritmo, tal y como se muestra a continuación:
Calculando la cantidad de memoria requerida dada la cantidad de celdas del espacio problema resulta:
Haciendo la conversión a GB nos queda:
Se calculó el número de operaciones del espacio problema, es decir, de la región de cálculo total.
Dado que N = 3906250000, entonces
Por lo tanto, el número de operaciones que debe realizar la computadora es de más de 35 millones, por esto es posible realizar este tipo de simulaciones en la actualidad, ya que la capacidad de las computadoras actualmente permite lograr esta cantidad de operaciones.
7. Resultados
Se obtienen como resultados numéricos la propagación del haz de luz en el interior de una fibra óptica para diferente número de iteraciones, primeramente se presentan las componentes de campo magnético Hx y Hy, ya que en el código fuente fue posible calcular de forma independiente, así como su suma vectorial para obtener el campo magnético total Ht. Se utiliza la interfaz gráfica de Matlab para mostrar las figuras, es importante resaltar que el algoritmo implementado es resultado de la investigación desarrollada por Calderón, Benavides, y Alamilla 5, 10, 14 y se ha enriquecido con la experiencia docente. Resulta un ejercicio interesante pedirle a los estudiantes que modifiquen cada parte de la fibra, desde el núcleo, los revestimientos, etc., posteriormente que modifiquen también la región de cálculo, en función del recurso de cómputo, dado que si construyen una región grande, el tiempo de obtención de resultados también aumenta considerablemente.
En la Fig. 5, se muestra la propagación del campo magnético Hx, logrando apreciarse cómo viaja la onda electromagnética en el interior de la fibra óptica, donde el núcleo no se modeló totalmente simétrico, de tal forma que la sección inferior del revestimiento no es exactamente igual a la parte superior. Aquí lo importante es mostrarle al estudiante que el aprendizaje no solo conlleva realizar el programa y manipularlo, sino que al observar los resultados obtenidos, corrobore que exista simetría y congruencia en la propagación electromagnética y de existir algún error pueda ser detectado de inmediato. Cada caso, implica un código nuevo, o por lo menos modificado y esto permite que los estudiantes logren un aprendizaje significativo.
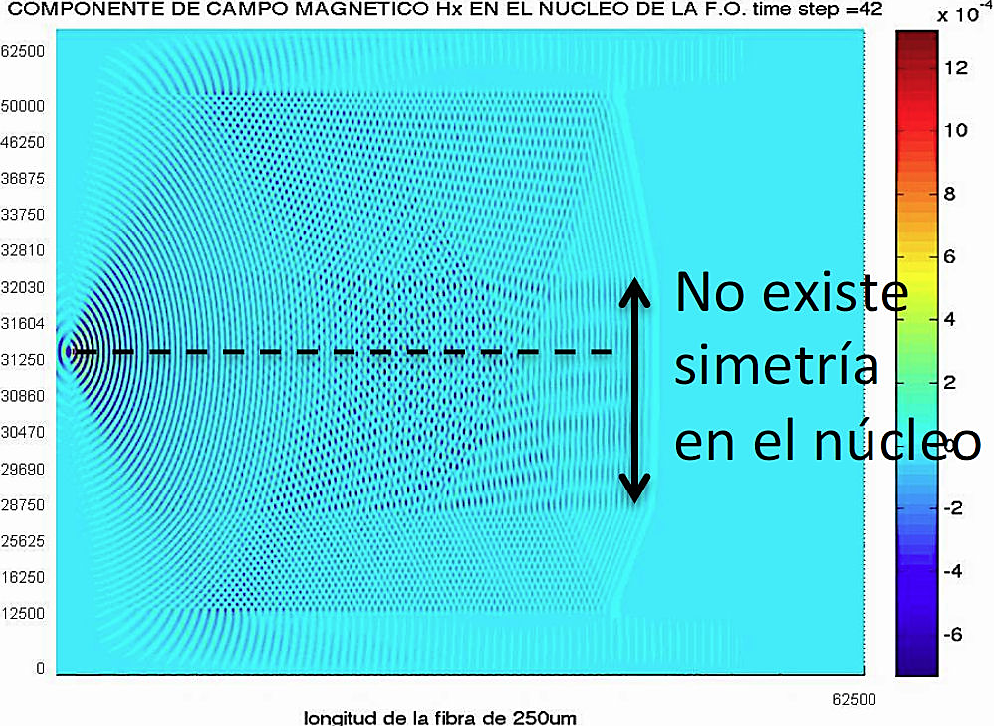
Figura 5 Ejemplo didáctico de un error al definir las capas de la fibra óptica, no existe simetría total en ellas.
En la Fig. 6, se muestra la componente de campo magnético Hx, Hy y Ht en el interior de la fibra, en la iteración número 950. Donde Ht es la suma vectorial de las componentes de campo Hx y Hy; en la Fig. 6a se observa la componente de campo magnético Hx, en la Fig. 6b la componente de campo Hy y en la Fig. 6c la componente de campo Ht, aquí también se distinguen de forma clara la fuente de alimentación y el núcleo. La región de cálculo se ha reducido a 1000 celdas en el eje X y 1000 celdas en el eje Y, debido al recurso de cómputo requerido, ya que el tiempo que destinan los estudiantes para este laboratorio, es limitado.
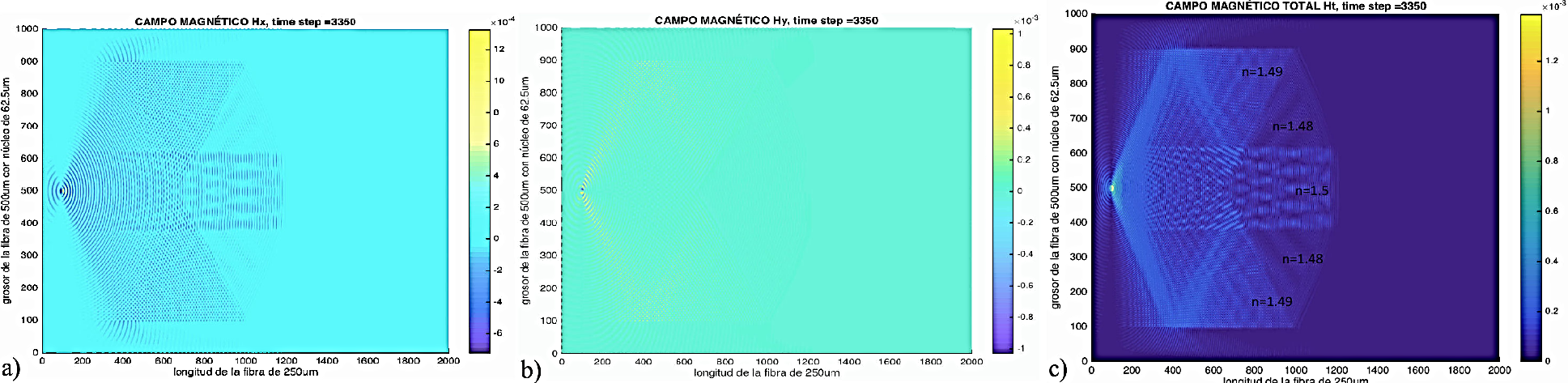
En la Fig. 7, se presenta el avance de la propagación, ahora en la iteración número 3350, en donde se puede apreciar la contribución de cada uno de los campos magnéticos, notándose el avance de la onda electromagnética, propagándose en el interior de la fibra óptica.
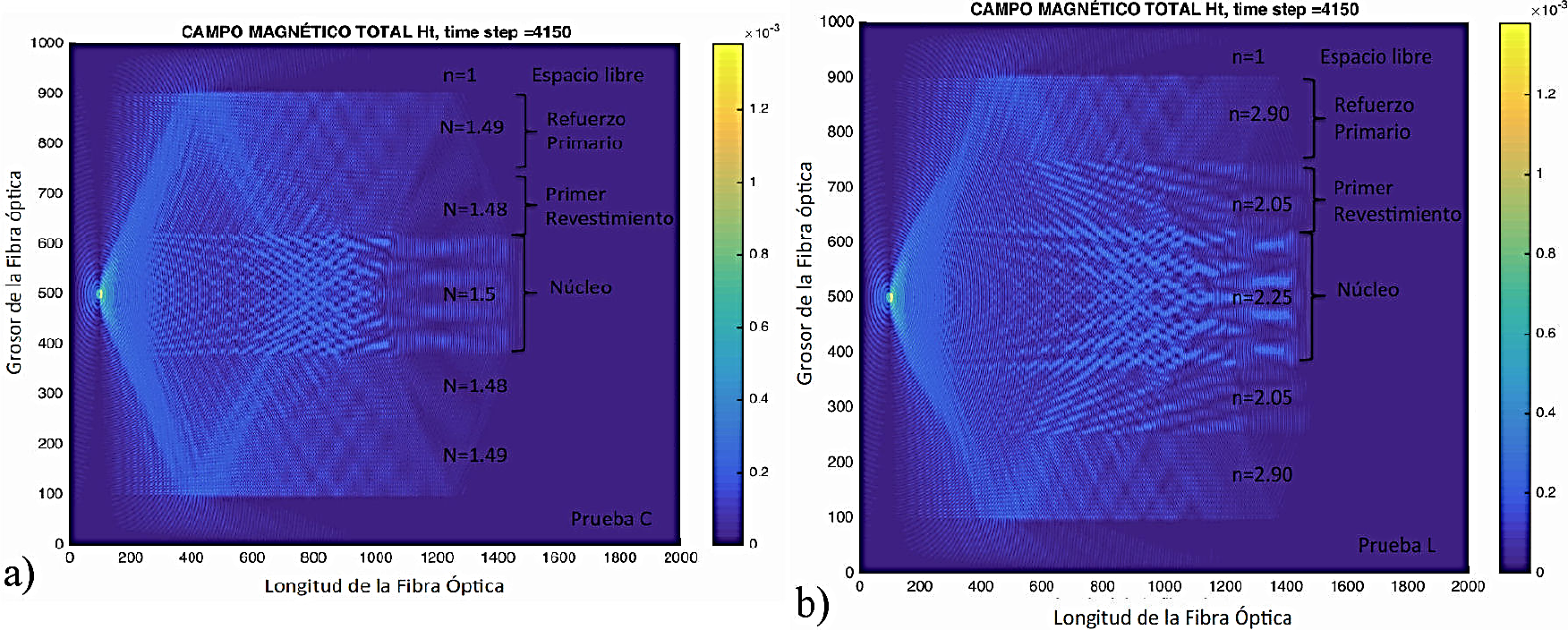
En la Fig. 8, en los incisos a, b, c, d, e, f, y g, se muestra la propagación de la onda electromagnética a lo largo de la fibra óptica, correspondiente a Ht, en 350, 1750, 2750, 3350, 5350 y 5950 iteraciones. En el inciso c, se definen cada una de las zonas que se modelan para este caso siendo éstas, el núcleo, el revestimiento, el refuerzo primario y el espacio libre de la región de cálculo. Cada una de estas zonas, con el índice de refracción, especificado en la Tabla I.
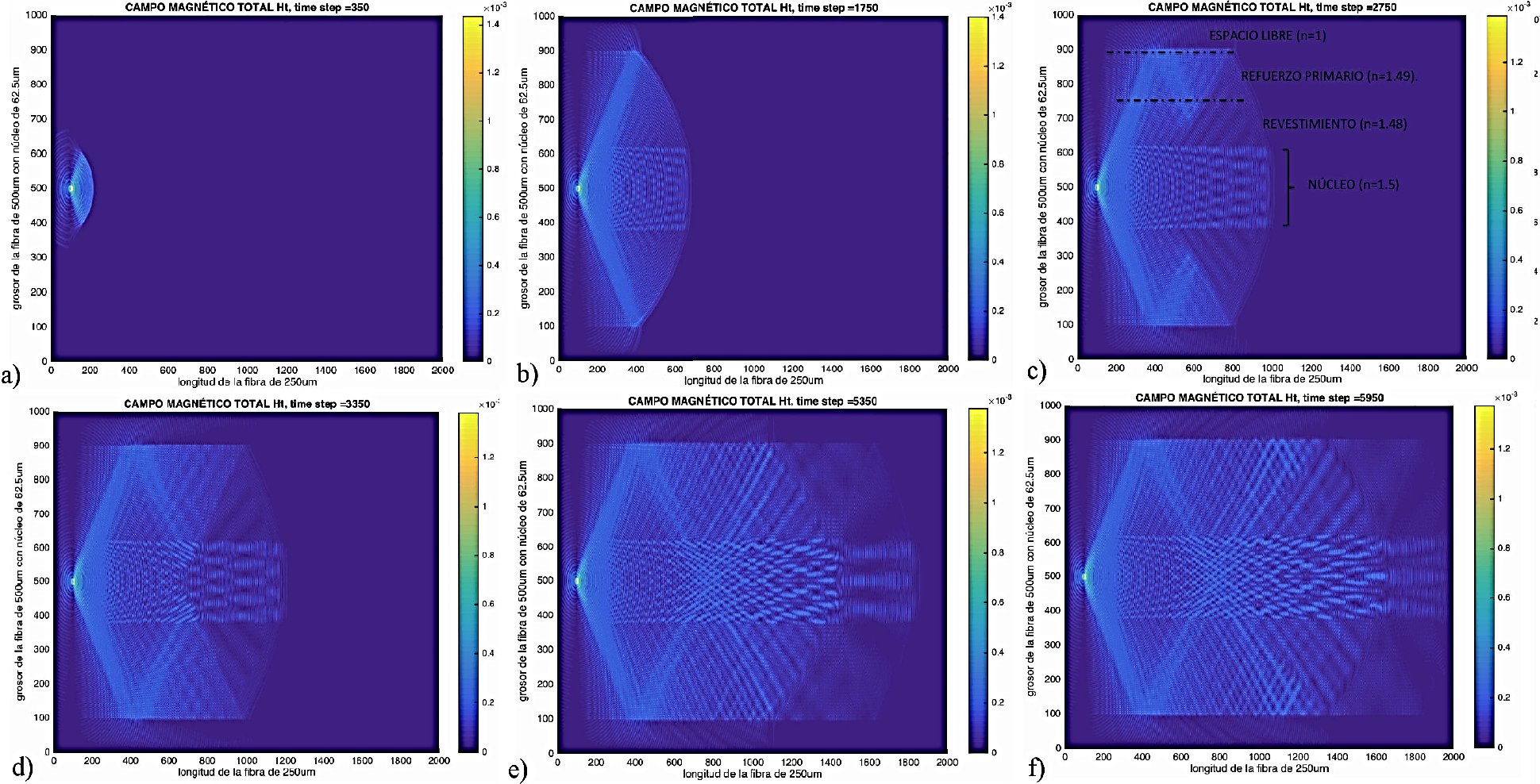
Figura 8 Propagación del campo magnético total Ht en el interior del núcleo de la fibra óptica a diferentes iteraciones.
Para fines didácticos, se presenta otra fibra óptica con las mismas características en cuanto a la región de cálculo, es decir, de 2000 celdas en el eje X y 1000 celdas en el eje Y, misma fuente de alimentación ubicada en las coordenadas, 99 en el eje X y 500 en el eje Y respectivamente. La diferencia radica en los índices de refracción para cada una de las capas de la fibra. En el Fig. 9 se presentan dos fibras ópticas, en el inciso a se considera la fibra que se ha estado documentando en el desarrollo del presente trabajo al cual se le ha llamado Prueba A; en el inciso b, se muestra los índices de refracción para la segunda fibra llamada Prueba B, de tal forma que se puede comparar el comportamiento de la señal electromagnética en el interior de cada una de ellas. Se puede apreciar que la capa del primer revestimiento con índice de refracción en la fibra Prueba B, es más visible que en el caso de la Prueba A. Como se sabe, los fenómenos de reflexión y refracción, dependen del paso de un medio a otro y de los valores de los índices de refracción de cada uno de ellos.
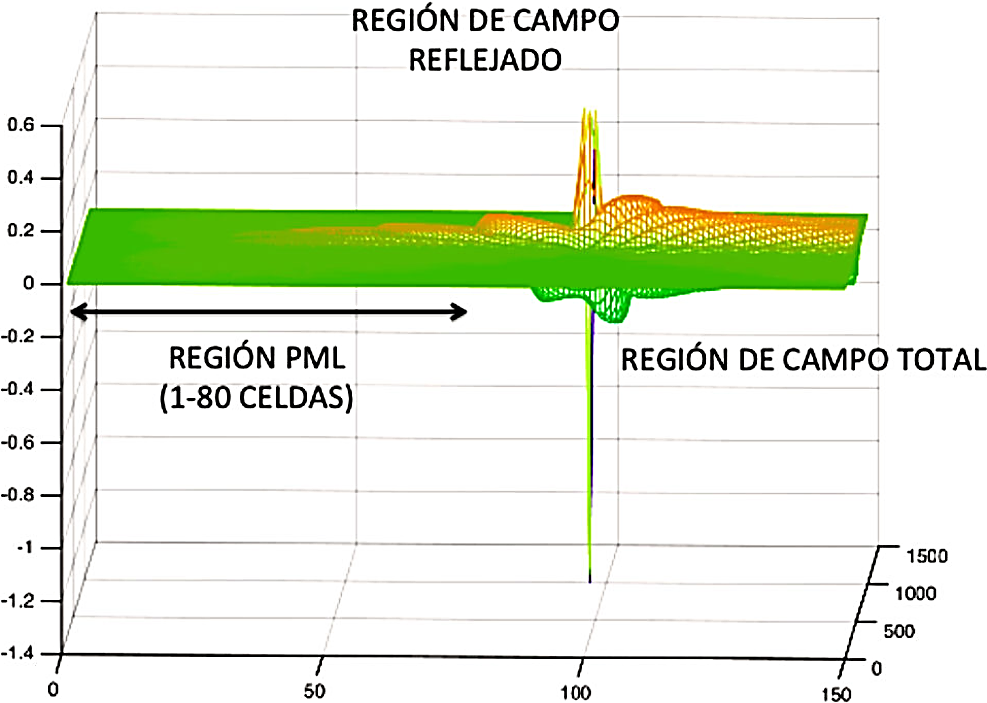
Por último, en la Fig. 10 se presenta la fuente de alimentación, vista desde la celda 0 hasta la celda 150, la ubicación de la fuente es en la celda (99, 500), es relevante señalar, que no existen señales espurias que afectan la precisión de las lecturas, ya que es claramente visible como en la región de campo reflejado (de la fuente hacia la izquierda) la señal se va atenuando hasta hacerse prácticamente cero, sin presentar reflexiones que hacia la región de campo total.
8. Conclusiones
Se ha realizado la simulación computacional de una fibra óptica multimodo con índice escalonado, obteniendo como resultados los parámetros electromagnéticos del sistema Hx, Hy y Ht. Desde el punto de vista didáctico, se ha realizado el modelado de una fibra formada solamente por el núcleo, el revestimiento y el recubrimiento, cada uno con su índice de refracción definido de acuerdo a las características de la fibra óptica descrita. La frecuencia de operación es de 187 THz y la longitud de onda es de 1600 nm. Con los resultados obtenidos es posible visualizar el fenómeno de propagación de un haz de luz dentro de la fibra óptica, de acuerdo a la reflexión y refracción que se presenta en función del índice de refracción de cada una de las capas de la fibra. El algoritmo de cómputo es robusto ya que permite modelar la propagación electromagnética en el interior de la fibra óptica, con índices de refracción variable en cada revestimiento, que el alumno puede variar para fines didácticos. La fibra óptica es alimentada mediante una función senoidal, aplicando en el código los requerimientos del método campo total- campo reflejado, el cual permite eliminar la propagación de señales espurias o parásitas que puedan afectar la precisión de la solución. Se presentan como resultados de la propagación de la señal electromagnética las componentes de campo magnético, Hx, Hy y Ht, a diferentes iteraciones, las cuales presentan un comportamiento de reflexión o refracción dependiendo del índice de refracción correspondiente a cada una de las capas que cubren la fibra óptica. Se muestra además la comparación de dos fibras ópticas, con diferentes índices de refracción en cada una de las capas que las forman, con la finalidad de que los estudiantes analicen el comportamiento de cada una de ellas. Por último se obtiene el comportamiento de la fuente de alimentación desde su punto de ubicación hacia la región PML, comprobando que no existen señales espurias que pueden afectar el comportamiento de la fibra óptica modelada dentro de la región de cálculo.
Al utilizar las herramientas del electromagnetismo computacional FDTD y PML, el estudiante logra un aprendizaje significativo, a partir de cambiar los parámetros del sistema y visualizar su efecto en la propagación de la señal en el interior de la fibra óptica, concluyendo que estos métodos son una opción viable para modelar este tipo de fenómenos.











 nueva página del texto (beta)
nueva página del texto (beta)