PACS: 02.30.Em; 12.39.Pn; 34.20.G
1. Introducción
Desde tiempos muy antiguos el hombre ha observado la belleza en las simetrías que existen en la naturaleza, preguntándose si hay alguna forma de imitarlas o al menos entenderlas con precisión, pero ¿Qué es la simetría? En física la simetría de un objeto se puede describir en términos del efecto de una operación (la cual puede ser continua o discreta), si el objeto (o el medio en el que éste se encuentra) se mantiene sin cambios después de ser aplicada la operación, se dice que hay una simetría involucrada. Más estrictamente hablando, la simetría tiene que ver con el efecto de la aplicación de operadores sobre un sistema y dependiendo de la respuesta obtenida se determina si hay o no una simetría, al haber o no un cambio en el sistema.
En el presente trabajo consideramos la siguiente simetría
en donde
i.e. el operador de paridad conmuta con el operador de Hamilton. Si las eigenfunciones del Hamiltoniano
2. Dos potenciales y más
2.1. Pozo doble de potencial finito
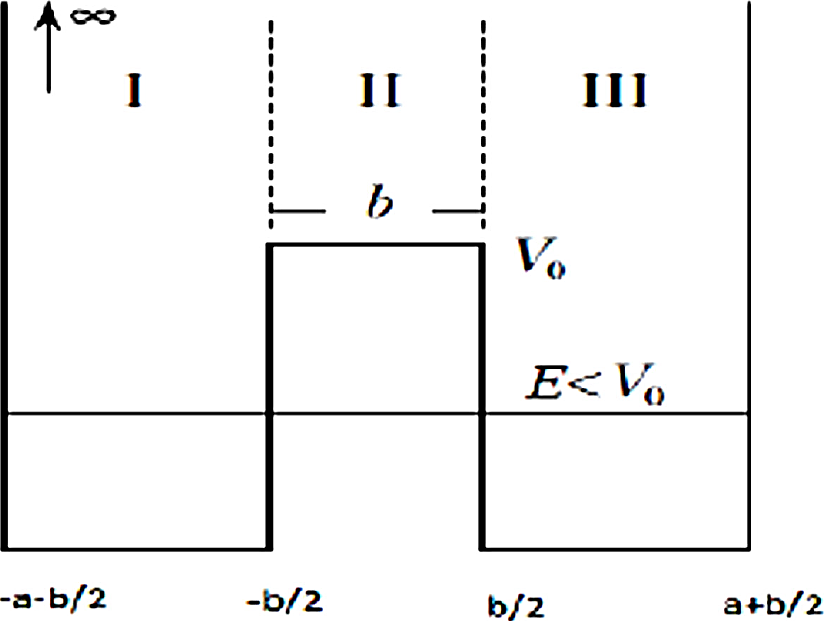
Consideremos una partícula de masa μ sometida a un potencial unidimensional V0(x), simétrico respecto al origen, como se muestra en la Fig. 1
La ecuación estacionaria de Schrödinger para las regiones I y III es
con k2 = (2μ/ℏ2)E, así las soluciones en estas regiones están dadas por:
región I (-l < x < -b/2)
región III (b/2 < x < l)
en donde l = a + (b/2).
Para la región II (-b/2 < x < b/2) la ecuación de Schrödinger está dada como sigue
donde, q2 =(-2μ/ℏ2)(E - V0(x)) con q > 0 puesto que E < V0(x) según se observa en la Fig. 1, y la solución para esta región es
Por otro lado, como el problema satisface la condición (1), estas soluciones deben tener una paridad bien definida, por lo tanto tendremos dos tipos de soluciones: la solución simétrica y la solución antisimétrica. Aún más, éstas estarán determinadas por las relaciones entre los coeficientes, respetando la continuidad de la función de onda y de sus derivadas.
SOLUCIÓN SIMÉTRICA
Así
La relación entre los coeficientes en la Ec. (2) se encuentra al aplicar las condiciones de continuidad en los puntos |x| = b/2.
Ahora bien, de la continuidad de ψs(x) y la continuidad de la (dψs(x)/dx), se obtienen las siguientes ecuaciones; en x = -b/2:
Continuidad de ψs(x)
De la continuidad de la dψs(x)/dx,
Al igualar (2b) & (2d) se obtiene la ecuación de cuantización para los estados simétricos:
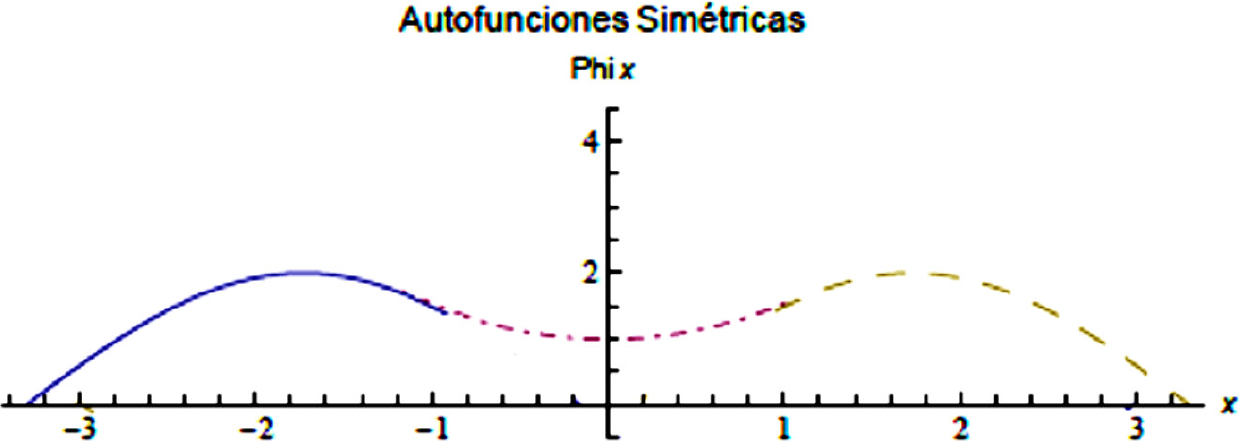
Figura 2 Representación gráfica de los estados simétricos. Línea rígida: región I, línea guion-punto: región II, Línea guion: región III.
Esta condición se encuentra representada en la Fig. 3 en términos del número de onda k. La solución de esta ecuación está determinada por la intersección de las curvas.

Figura 3 Los puntos de intersección determinan el valor permitido para la energía del estado simétrico. Línea punteada f(k) = −(1/(1 − k2)1/2) coth((1 − k2)1/2/2). Línea solida f(k) = (1/k) tan k. a = b = 1, (2µ/ℏ2)V0(x) = 1.
SOLUCIÓN ANTISIMÉTRICA
Así
De manera análoga a los estados simétricos, consideramos la condición de continuidad para la función de onda y su derivada en x = -b/2 (es importante destacar que el resultado es el mismo al considerar el punto x = b/2).
Continuidad de ψa(x)
Continuidad de la derivada de ψaintersección determinan los valores permitidos para las (x)
así que
Al igualar (3b) & (3d)
se encuentra la condición de cuantización para los estados antisimétricos la cual se ilustra en la Fig. 5.
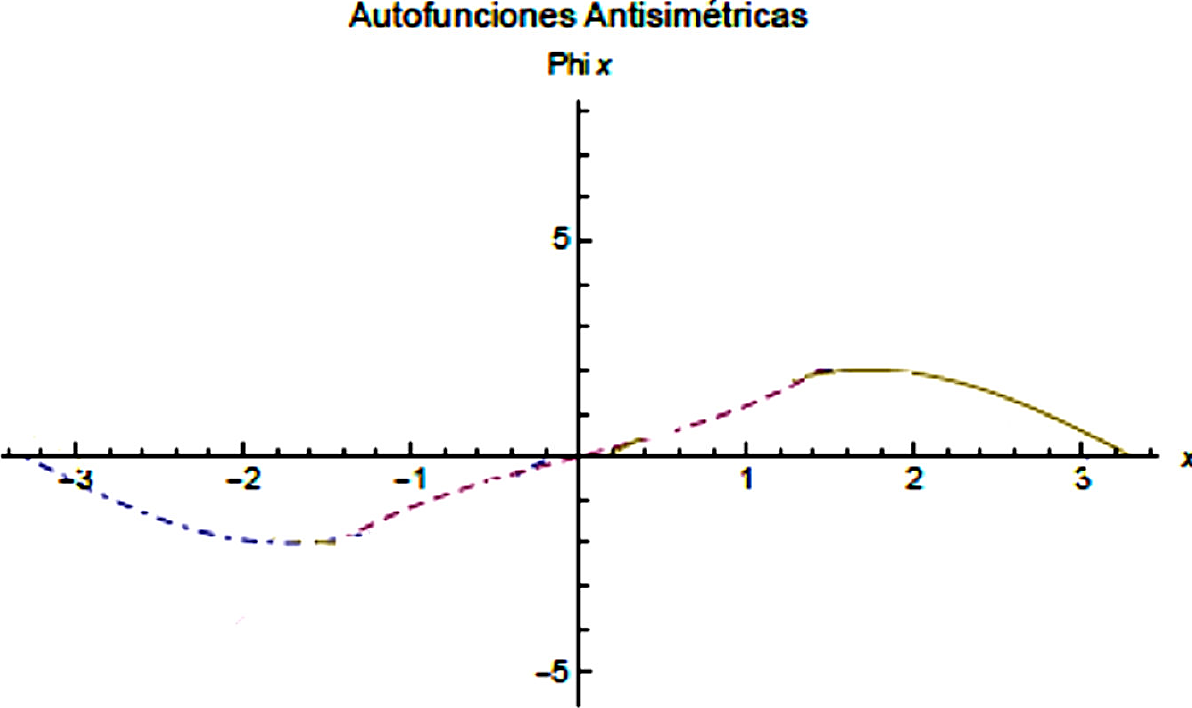
Figura 4 Representación gráfica de los estados antisimétricos. Punto-guion: región I, Guion: región II, Solido: región III.
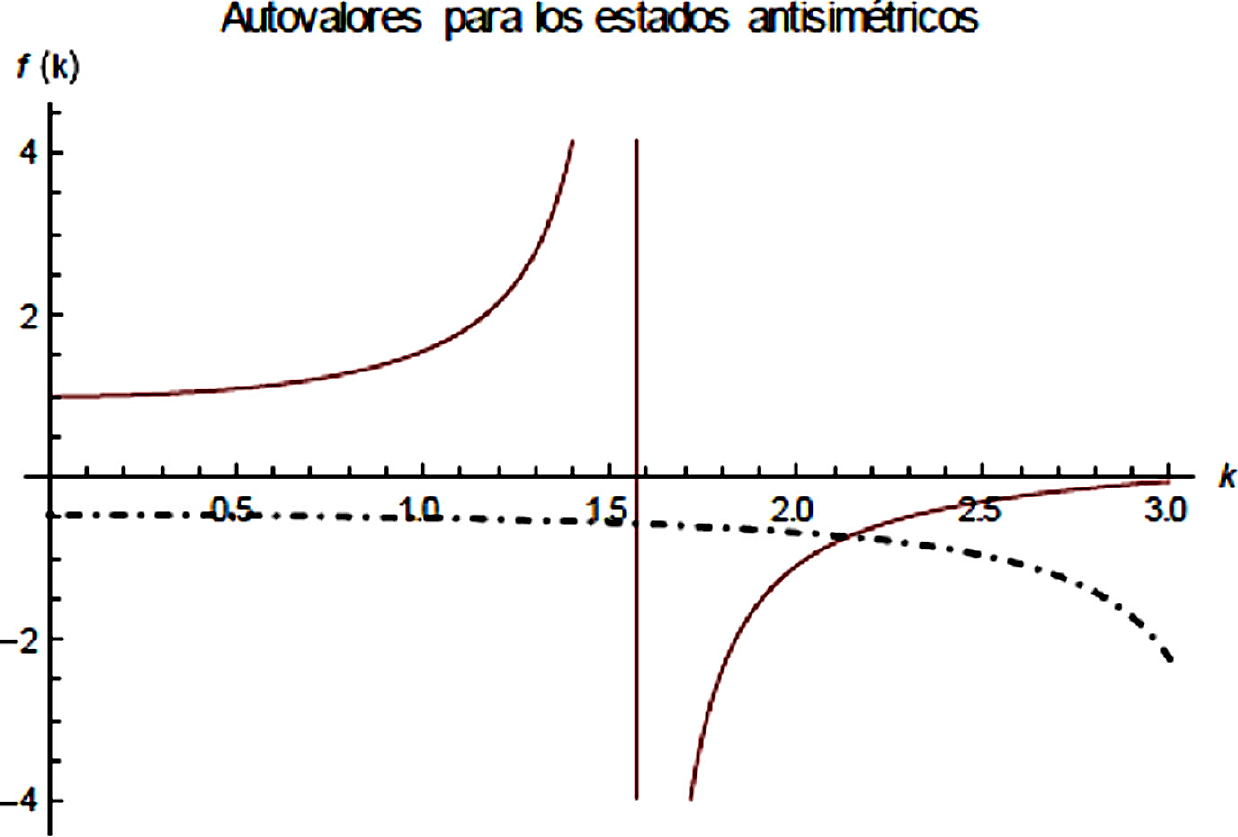
Figura 5 Los puntos de intersección corresponden al valor permitido para la energía del estado antisimétrico. Línea guion-punto f(k) = −(1/(1 − k2)1/2) tanh((1 − k2)1/2/2). Línea solida f(k) = (1/k) tan k. a = b = 1, (2µ/ℏ2)V0(x) = 1.
En las Figs. 6 mostramos, para su comparación, los valores de las energías permitidas Es y Ea , a través de k, para dos valores diferentes de potencial.
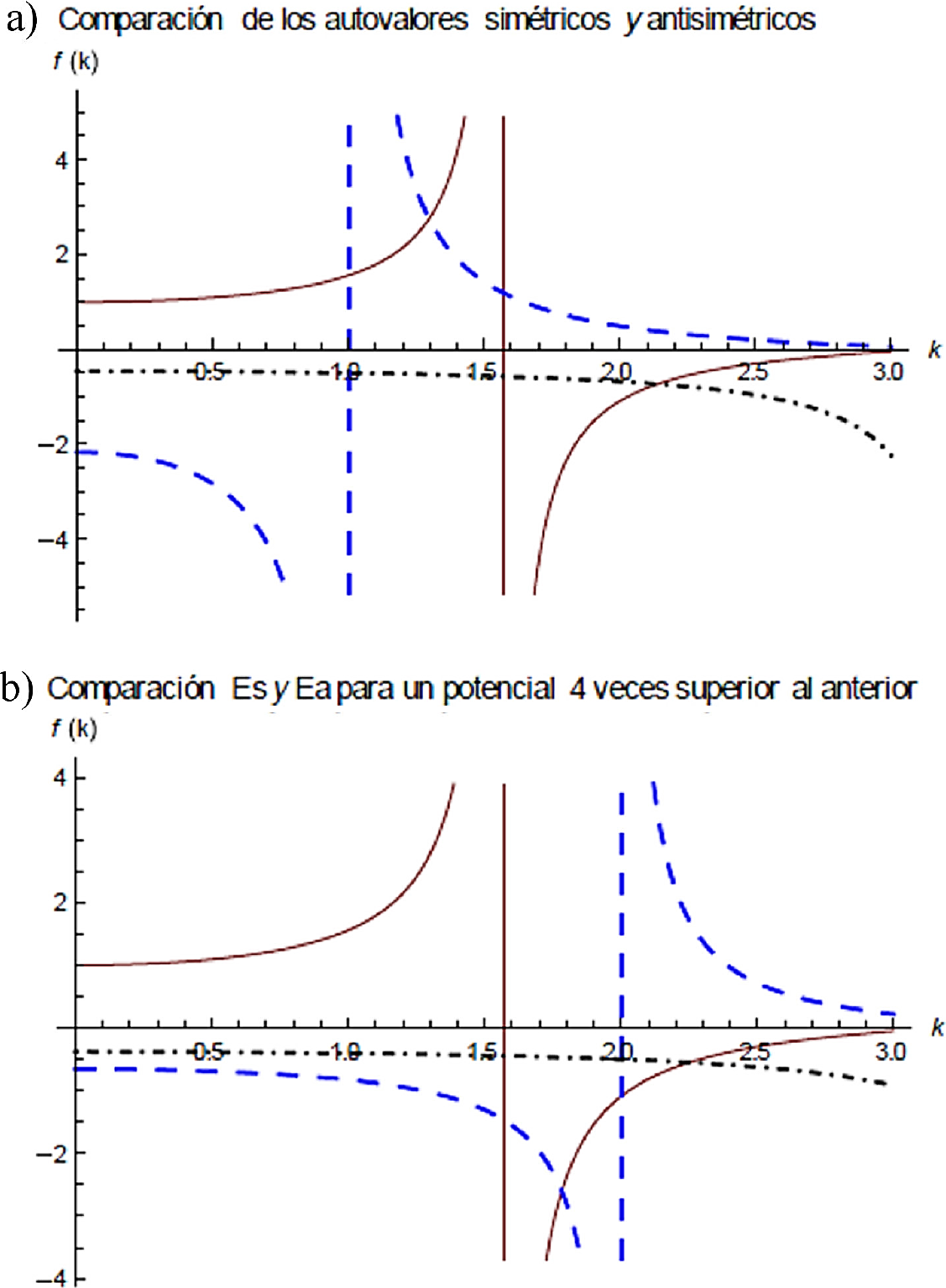
Figura 6 Los puntos de intersección determinan los valores permitidos para las energías asociadas a los estados simétricos y antisimétricos en términos de k. Línea solida f(k) = (1/k) tan k, a) línea punteada f(k) = −(1/(1 − k2)1/2) coth((1 − k2)1/2/2), línea punto-guion f(k) =−(1/(1 −k2)1/2) tanh((1 − k2)1/2/2). a = b = 1, (2µ/ℏ2)V0(x) = 1. b) línea punteada f(k) =−(1/(4 − k2)1/2) coth((4 − k2)1/2/2), línea punto-guion f(k) =−(1/(4 − k2)1/2) tanh((4 − k2)1/2/2). a = b = 1, (2µ/ ℏ2)V0(x) = 4.
Al comparar las Figs. 6a y 6b, se puede apreciar que hay un corrimiento en los valores de la energía. Más adelante ilustraremos gráficamente, el comportamiento de las energías Es y Ea en términos de la evolución de las condiciones de cuantización, en relación al potencial.
Por el momento, nos ocupamos de las condiciones de cuantización dadas en las Ecs. (2e) y (3e), con el propósito de analizar, analíticamente, las circunstancias en las que se presenta la degeneración cuántica, es decir Ea = Es .
La Ec. (2e) equivale a
y la (3e)
Ellas difieren en los signos, pero se las puede escribir de manera simultánea como sigue
A cada simetría le corresponde un signo. El signo superior (inferior) es para el caso simétrico (antisimétrico). Desarrollando la parte derecha de la ecuación anterior
obtenemos
Ahora bien, si: (2μ/ℏ2)V0 ≫ k2 y q2 ≫ k2 pues q2 = -k2 + (2μ/ℏ2)V0 ⇒ q2 ≃ (2μ/ℏ2)V0, entonces en este límite
Por lo tanto, cuando el potencial es grande comparado con la energía
En el límite V0 → ∞
Por lo tanto a medida que crece el potencial, las energías se van acercando mucho una a la otra, llevando al fenómeno de degeneración o equivalentemente ka ≃ nπ2 como en el caso del potencial infinito.
Si comparamos las condiciones de cuantización obtenidas en el caso simétrico (2e) y antisimétrico (3e) (el lado derecho de estas ecuaciones), se observa en la Fig. 7, que aparece un acercamiento entre los valores de las funciones que determinan la cuantización de la energía a medida que q y por ende el potencial V0(x) crecen, hasta el límite en el que éstas coinciden, presentándose la degeneración cuántica. Es importante destacar que en el límite en el que el potencial es infinito, la naturaleza del problema cambia radicalmente, ya no se presenta el efecto túnel, es decir, los pozos son incapaces de comunicarse, por lo tanto, el problema se transforma en el de dos pozos completamente independientes, y debido al aislamiento no se manifiesta una degeneración.
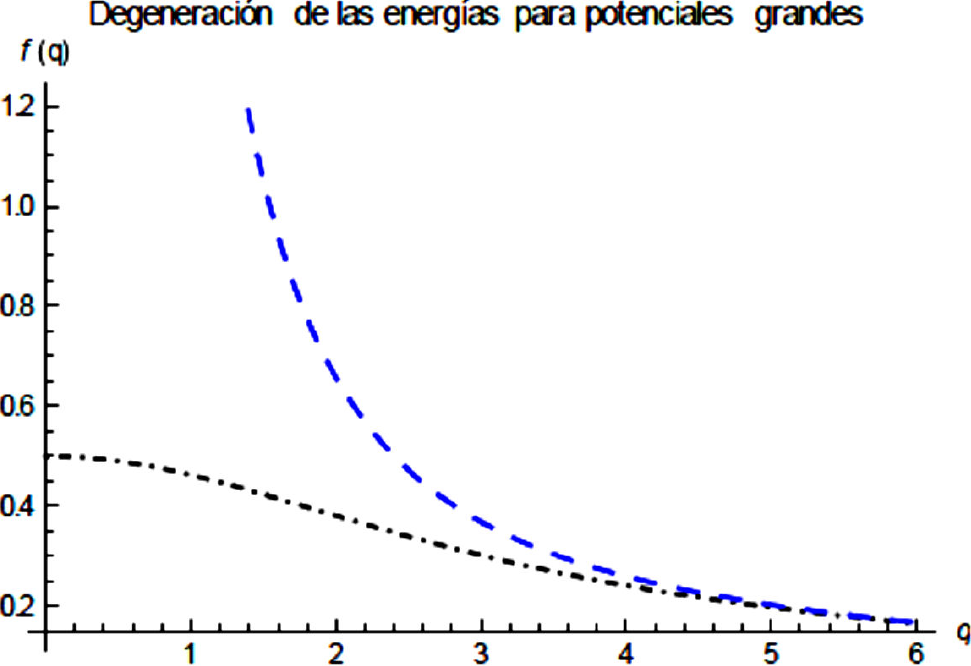
Figura 7 Comparación de las funciones que determinan la energía para los estados simétricos y antisimétricos. Línea punteada f(q) = (1/q) coth(q/2), Ec. (2e). Línea punto-guion f(q) = (1/q) tanh(q/2) Ec. (3e). b = 1.
SUPERPOSICIÓN DE ESTADOS
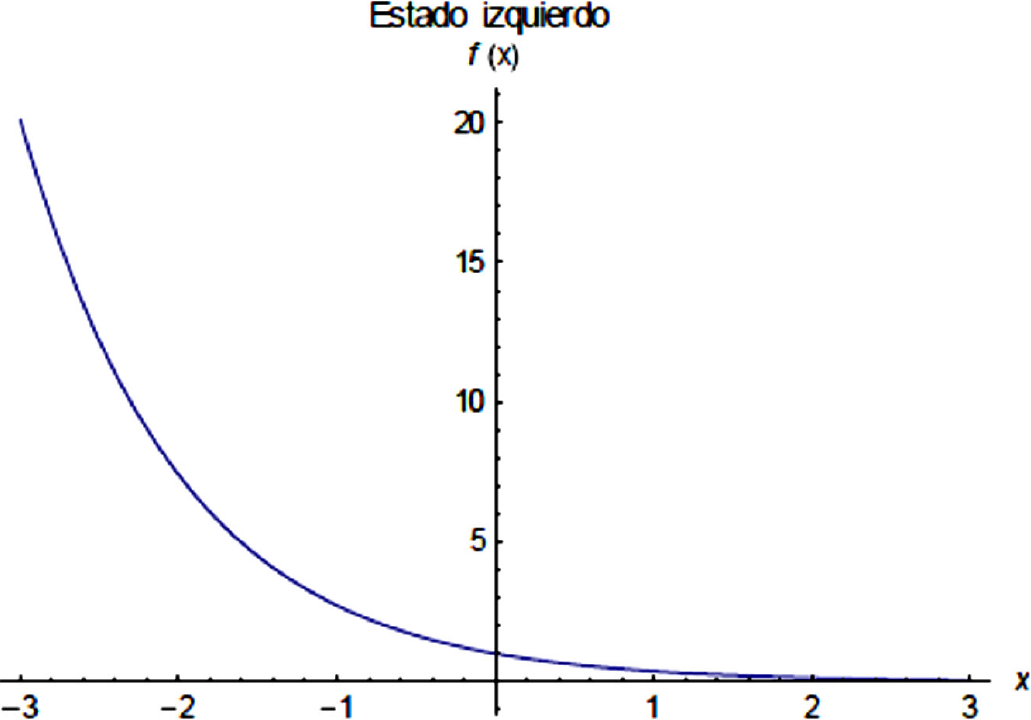
Consideremos ahora que el sistema se encuentra en los estados: ψs (x) + ψa (x) y ψs (x) - ψa (x), que por sus características los denotaremos como ψL (x) y ψR (x) respectivamente, dado que en estos nuevos estados la partícula se encuentra del lado izquierdo -l < x < -b/2 (zona I), o del lado derecho b/2 < x < l (zona III) de la Fig. 1, de acuerdo a, a).
Sustituyendo los valores de los coeficientes Bs y Ba , (2b) y (3b), en términos de As tenemos
Graficando la solución de la zona II de la Fig. 1, es decir, la parte central de esta ecuación, podemos observar que el comportamiento corresponde a una acumulación del sistema en el lado izquierdo.
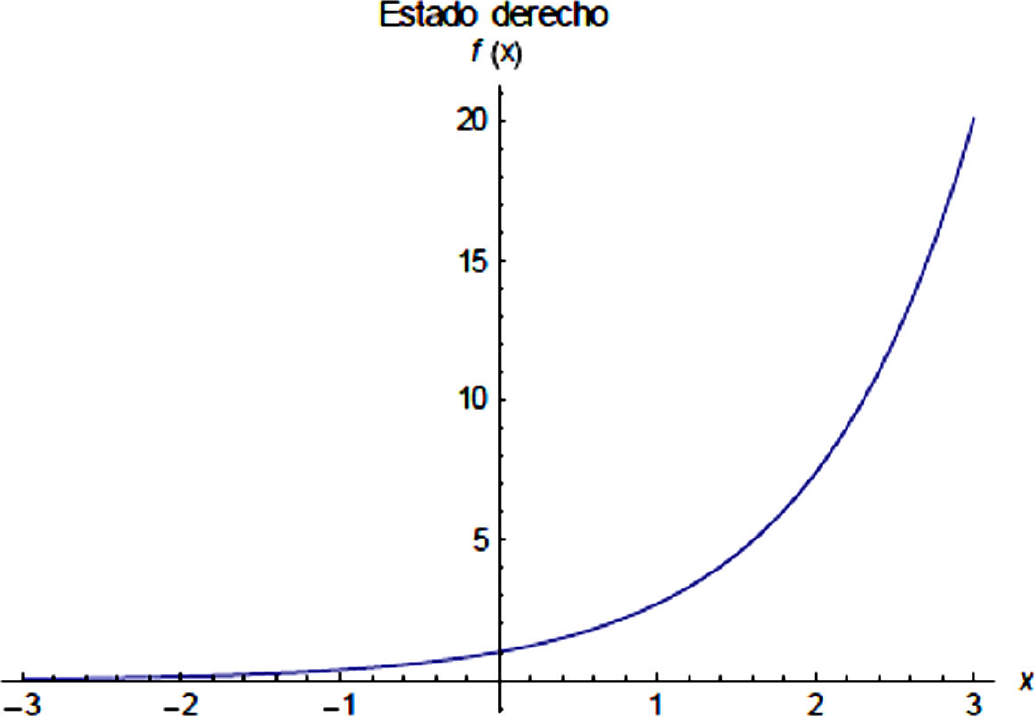
y al sustituir los coeficientes Bs y Ba ,
Se ve que la acumulación se da en el lado derecho, y la solución en la zona II se ilustra en la Fig. 9.
Ahora resulta que estos nuevos estados no son eigenestados del operador de paridad, de hecho al aplicar el operador de paridad a los estados ψL(x) y ψR(x), estos son intercambiados, y estos estados tampoco son eigenestados de la energía.
Vamos a asumir que al tiempo t=0 el sistema se encuentra en el estado ψL(x,T = 0). Si queremos saber cómo ha evolucionado este estado temporalmente, utilizamos el operador de evolución temporal
Notamos que el sistema oscila con una frecuencia
Cuando transcurre un lapso de tiempo igual a la mitad del periodo T = 2πℏ/(EA - ES) el sistema sufre una transición y se encuentra en un estado puro derecho ψR y al tiempo T regresa al estado ψL , así el sistema se encuentra oscilando, entre ψR y ψL indefinidamente 1. Debido a la naturaleza cuántica del problema, la partícula puede atravesar la región clásicamente prohibida y cambiar de un estado a otro.
Ahora nos preguntamos ¿Qué sucede si la barrera de potencial finita V0(x) se torna casi infinita? Cuando esto sucede, como analizamos anteriormente, a los estados ψs(x) y ψa(x) les corresponde la misma energía, son estados degenerados, y aunque sean eigenestados de la energía, ya dejan de serlo para la paridad y ya no hay posibilidad de tunelaje a través de la barrera. Una vez que el sistema se encuentre en el lado derecho o izquierdo ahí permanecerá para siempre. Se ha roto la simetría.
2.2. Pozo doble tipo delta de Dirac
Vamos a enfocar ahora nuestra atención en un problema análogo al estudiado anteriormente.
Consideramos el estudio del comportamiento cuántico de una partícula de masa μ sujeta a un potencial unidimensional del tipo:
Donde P es una constante adimensional positiva que representa a la profundidad de los pozos de potencial, δ(x) es la función delta de Dirac y a es una longitud constante. Ver Apéndice y Fig. 10.
El propósito es entender con detalle el problema, y al igual que en el problema anterior, formular las soluciones analíticas (estados ligados) en función de P. Este problema además de interesante, es útil por sus importantes aplicaciones prácticas y posible entendimiento de la presencia de algunos materiales asimétricos (moléculas orgánicas e isómeros ópticos) que existen en la naturaleza.
Las soluciones explícitas de la ecuación de Schrödinger
La Solución Simétrica ψS(x), tal que
Aquí k2 = -2μE/ℏ2, para estados ligados E < 0.
Esta solución (ver Fig. 11), debe satisfacer la condición de continuidad en x = ± - a, por lo que BS = (1/2)AS (exp(-ka)/cosh(ka)).
La condición de cuantización para la energía ES , en este caso, surge al considerar la discontinuidad de las derivadas (nótese que en esta condición el problema difiere del anterior) en los puntos x = ±a, debido a las características de la función delta de Dirac (Ver Apéndice). La condición de cuantización ahora resulta
La Solución Antisimétrica ψA(x), tal que
Esta solución, satisface la condición de continuidad en x = ± a, por lo tanto BA = -(1/2)AS (exp(-ka)/sinh(ka)). (Ver Fig. 12).
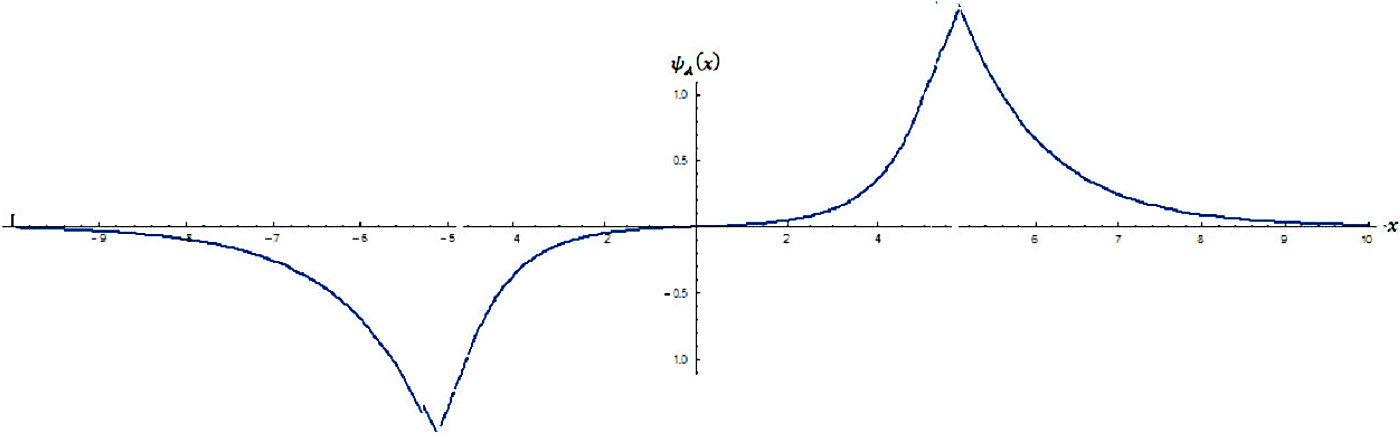
Figura 12 Representación gráfica de los estados antisimétricos para un potencial del tipo (8), para AS < 0.
La condición de cuantización asociada a EA también surge al considerar la discontinuidad de las derivadas en x = ±a y resulta (Ver Apéndice)
Es interesante analizar la solución gráfica simultánea de las condiciones de cuantización para las Ecs. (10) y (12) (Fig. 13), asociadas a los estados ψS(x) y ψA(x). En esta figura, el eje vertical corresponde al valor de P. Se nota que las energías asociadas al estado ψA(x) y al estado ψS(x), satisfacen la relación EA > ES y se van acercando a medida que la profundidad del potencial P va aumentando. Es decir, para cierta profundidad existe una degeneración en la energía EA → ES . Esto tiene una repercusión importante asociada a los autoestados de la simetría de paridad.
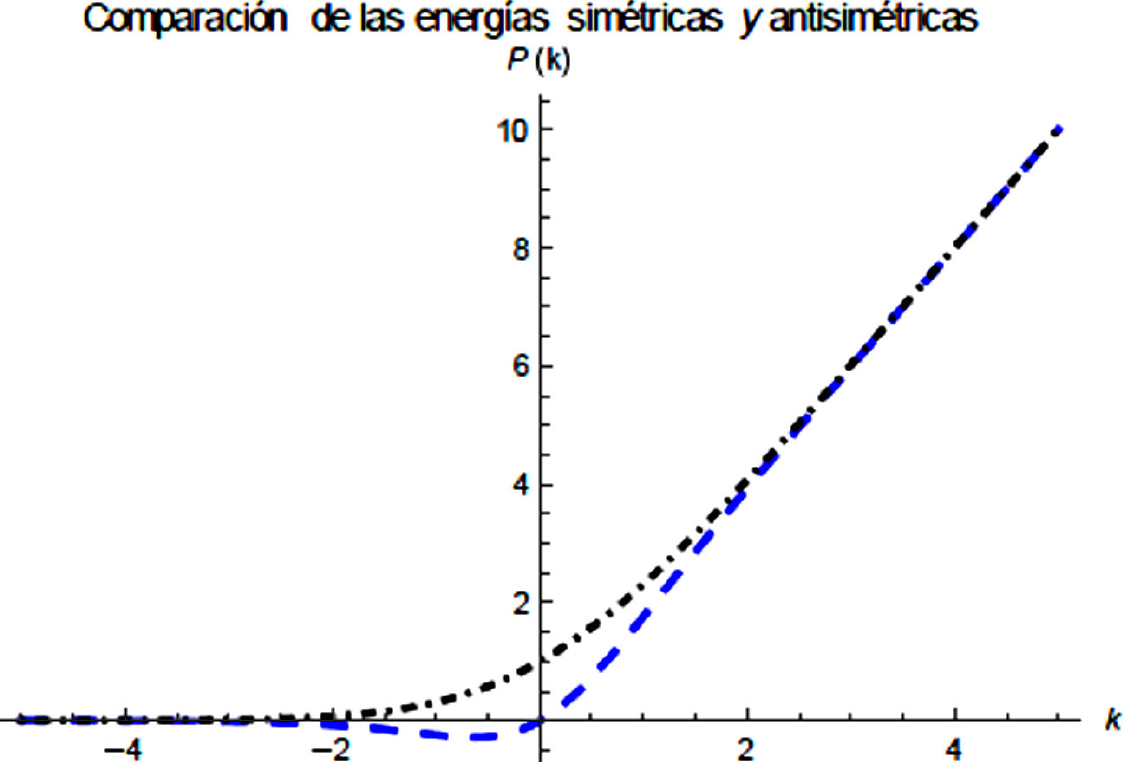
Figura 13 Gráfica simultánea de las condiciones de cuantización para los estados simétrico, línea punteada Ec. (10) y antisimétrico, línea punto-guion, Ec. (12). P corresponde a la profundidad del potencial.
Consideremos en este momento que el sistema se encuentra en un estado relacionado con la suma de las soluciones Simétrica y Antisimétrica,
Sustituyendo los valores
Ahora, para ψR (x) = [ψs (x) - ψa (x)] se obtiene
la cual se reduce a
Las funciones ψR(x) y ψL(x) satisfacen correctamente las condiciones de continuidad en x = ±a.
Estos nuevos estados ψR(x) y ψL(x) se concentran en el lado derecho e izquierdo respectivamente, más aún, la parte central de ψR (x) y ψL(x), tiene exactamente el mismo comportamiento que el del problema del pozo doble finito de potencial simétrico, con lo que podemos afirmar que el comportamiento en los dos problemas es análogo en general, por lo tanto, estos estados tampoco son autoestados del operador de paridad y ante el operador de paridad se transforman uno en el otro, y por lo tanto, estos nuevos estados no estacionarios, estarán oscilando con una frecuencia ω = (EA - ES /ℏ) (las energías ES y EA están dadas a través de las Ecs. (10) y (12) respectivamente).
Como se trató anteriormente, a medida que la profundidad de los pozos aumenta las energías se
acercan una a la otra y el sistema se “degenera” EA
= ES
desapareciendo la oscilación. En este caso, tanto
ψL(x,t)
como ψR(x,t) son
autoestados de la energía, a pesar de que siguen sin ser autoestados de la
Paridad. Estos estados permanecerán un tiempo infinito sin cambiar. La asimetría
subsiste eternamente. Nuevamente la simetría de paridad ha sido rota. Lo
anterior es posible a pesar de la simetría del Hamiltoniano y de que los
operadores de energía y paridad conmuten entre si
Teorema Suponga que
Entonces ψn es también un eigenestado de la paridad.
Sin embargo, cuando hay degeneración se rompe la simetría de paridad.
Las consecuencias prácticas del comportamiento de las funciones de onda, para los potenciales estudiados, se manifiestan en algunas moléculas orgánicas, en particular nos enfocamos en la molécula de amoniaco NH3, la cual está compuesta por un átomo de nitrógeno y tres átomos de hidrógeno formando una pirámide.
La interacción entre el átomo de nitrógeno y los de hidrógeno de esta molécula puede modelarse mediante un doble potencial de oscilador (similar a los aquí tratados) como se muestra en la Fig. 14 4. En las soluciones que hemos presentado, detallamos el comportamiento de los sistemas en las zonas clásicamente prohibidas, es decir, zonas en las cuales la energía total es inferior al valor del potencial E < V y mostramos que sí existe una probabilidad de ocupar o atravesar esa zona por efecto túnel, puramente cuántico.
Como se mostró en los casos anteriores, los estados, dada la simetría del potencial (en este
caso, relativa al plano formado por los átomos de hidrógeno), son autoestados
simultáneos del Hamiltoniano
En ambos casos, las probabilidades |ψ(s,a)(x)|2 máximas para localizar al átomo de Nitrógeno N se encuentran en x = ±a como lo sugieren las Figs. 2 y 4.
En la naturaleza, la molécula de amoniaco en equilibrio, se encuentra en dos configuraciones diferentes como lo muestra la Fig. 14. En una de ellas N se encuentra en x = -a y en la otra en x = a es decir, abajo o arriba del plano de simetría. En otras palabras, el sistema se encuentra en los estados ψL(x) ó ψR(x). Por efecto túnel el nitrógeno atraviesa la barrera de potencial una y otra vez pasando, al transcurrir el tiempo, de una configuración a la otra con una frecuencia determinada en (7) proporcional a la diferencia de energías entre la del estado base Es y la del primer estado excitado Ea, que corresponde a una frecuencia de oscilación de 24,000 MHz 1 que se encuentra en la región de microondas. En un gas de estas moléculas se encuentran, en igual proporción, estados en ambas configuraciones y es mediante un campo eléctrico no uniforme que es posible separar los átomos en estado base de los que se encuentran en el estado excitado. Así se produce una gran concentración de moléculas excitadas, las necesarias para que al des-excitarse de manera espontánea, se induzca en cascada, la emisión de radiación coherente (fotones de igual frecuencia) 5.
A la fuente de radiación coherente en forma de microondas se la conoce como “máser” (siglas de amplificación de microondas mediante la emisión estimulada de radiación). El máser, en efecto, produce una emisión coherente de microondas; esto es, radiación altamente concentrada, de una única longitud de onda.
Aparte de la utilidad cotidiana del máser, las microondas se encuentran presentes en importantes experimentos científicos, en particular, en una primera prueba exitosa de un dispositivo para fusión realizada en el Instituto Max Planck en Greifswald, Alemania 6. Este experimento podría ser un inicio para la generación de energía nuclear renovable, barata, limpia y segura, a través de la fusión nuclear. En este experimento fueron usados un equivalente a 6000 hornos de microondas para fusionar átomos de hidrógeno y producir un plasma que sería la fuente de producción de energía nuclear. Es importante señalar también que el efecto túnel, es esencial para la operación de muchos dispositivos modernos que influyen en nuestro mundo, en una escala desde la atómica hasta escalas de proporciones galácticas. En este trabajo hemos mostrado, particularmente, el papel que juega este efecto en la operación de máser de amoniaco.
3. Conclusiones
Al comparar las Figs. 2 y 11, asociadas a los estados simétricos del pozo doble finito y del pozo doble delta de Dirac, respectivamente, observamos que el comportamiento ante ambos potenciales es en esencia el mismo, sin embargo, como se aprecia en las figuras, la diferencia radica en la suavidad de las curvas para el primer caso y en los picos asociados a la discontinuidad de la derivada del segundo caso; este mismo razonamiento se sigue para los estados antisimétricos y para el tercer caso relacionado con el NH3.
Es importante señalar que al comparar las Figs. (7) y (13), se observa que expresan el mismo comportamiento, esto es, las energías asociadas a los estados simétricos y antisimétricos se acercan conforme la profundidad del pozo crece, es decir, aparece degeneración para potenciales muy grandes (sin considerar el caso límite en el infinito, pues si esto ocurre, como ya se mencionó antes, los pozos se vuelven independientes).
Mostramos que cuando se superponen los estados simétricos y antisimétricos obtenidos, se rompe la simetría, lo cual en un principio podría causar cierta conmoción, sin embargo, como se ha mostrado en el desarrollo de los estados derecho e izquierdo, es gracias a la formación de estos estados que se puede dar origen a ciertos fenómenos físicos, o más bien, a la correcta descripción de fenómenos que observamos comúnmente en la naturaleza. Así la simetría debe romperse para dar lugar a cosas nuevas, y de aquí, ya no resulta tan extraño suponer por qué el azúcar que endulza nuestro café por las mañanas tiene orientación izquierda, o que nuestro corazón se encuentre del lado izquierdo de nuestro cuerpo. Finalmente, este trabajo intenta por un lado, mostrar la importancia de la simetría y su rompimiento, y por otro lado destacar la importancia del efecto túnel, para con ambas herramientas, dar una explicación a esos pequeños detalles, que día a día están presentes en nuestro entorno, que pocas veces cuestionamos pues ya los damos por hecho, pero que es con base en estas sutilezas que el mundo funciona tal como lo conocemos.











 nueva página del texto (beta)
nueva página del texto (beta)