PACS: 03.65.Ud
1. Introducción
Cualquiera que sea la posición que uno tome en la discusión, la teoría cuántica es ciertamente sorprendente en su quiebre radical con respecto a otros campos de la física. No sólo exhibe indeterminaciones, sino que la teoría conlleva a una negación esencial de la objetividad, un abandono del realismo. Este último punto nace del hecho de que la teoría cuántica ofrece una descripción ínfima de los sistemas físicos aparte de lo que sucede durante procesos de medición 1. Con todo esto, se vuelve claro que la búsqueda por una teoría realista de los fenómenos cuánticos es un tema que atrae gran interés. Mientras esa posibilidad surge, un tema que viene a la mente son los llamados “teoremas de no variables ocultas”, que generalmente se pueden ver como argumentos que muestran evidencias en contra del realismo. Las enigmáticas desigualdades de Bell 2 son un caso de estos teoremas y han sido probadas experimentalmente en repetidas ocasiones 3-13, incluso han sido llamadas por algunos como uno de los logros más impresionantes de la ciencia.
Las desigualdades de Bell son un conjunto de desigualdades que ayudan a marcar una diferencia entre las predicciones que se tienen entre teorías de variables ocultas locales y la mecánica cuántica. Al derivar las desigualdades de Bell las suposiciones más importantes que se hacen son:
Los parámetros tienen realidad independientemente de si son medidos o no, i.e. existe una realidad separada de su observación.
Localidad, la información no puede viajar más rápido que la velocidad de la luz.
La violación de la desigualdad de Bell implicaría que al menos una de las dos suposiciones anteriores es falsa. Pasarían 17 años a partir de la publicación del artículo de Bell2 y la primer confirmación experimental de su teorema. Entre 1981 y 1982 Alain Aspect junto con su grupo de estudiantes en Orsay 14-16. demostraría que la desigualdad de Bell se viola, terminando así el legado de 46 años de la paradoja de EPR 17 y comenzando la búsqueda de experimentos libres de huecos (loopholes) que confirmaran los resultados de Aspect.
Este tema es con frecuencia omitido en los cursos de mecánica cuántica a nivel licenciatura. Es con el fin de presentar a los estudiantes estas ideas, así como acercarlos a la mecánica cuántica experimental que se propone el experimento detallado en este artículo, dicho experimento se basa en pares de fotones con polarizaciones entrelazadas tal y como se crean en Ref. 18. Una discusión más educativa se puede encontrar en Ref. 19. El hecho de que la alineación y ejecución del experimento tomen tan solo un par de horas es ideal para una primera aproximación a la mecánica cuántica experimental por parte de los estudiantes, que al final pueden comprobar con un análisis muy simple la veracidad del teorema de Bell. Así como exponerlos por primera vez a los estados enredados, utilizados en la teleportación cuántica, codificación superdensa, criptografía cuántica…, entre otros efectos notables.
En el presente experimento se utilizó la desigualdad de CHSH 20 para probar el teorema de Bell
en donde E es el valor esperado de la correlación cuántica y se calcula de la siguiente forma
siendo N el número de coincidencias obtenidas para dicha configuración. El parámetro de Bell S no tiene un significado físico claro, sino que se refiere a correlaciones entre mediciones separadas, lo cual, al final puede relacionarse con el número de eventos observados. Sin embargo su importancia recae en el hecho de que, para una teoría de variables ocultas locales, su rango se encuentra restringido entre -2 y 2, dicho de otra forma, una teoría de este tipo tendría correlaciones de tal manera que en todo momento se cumpla |S| ≤ 2.
2. Creación del estado enredado
Como ya se comentó anteriormente, en nuestro experimento se utilizaron pares entrelazados de fotones, en donde el entrelazamiento venía dado por polarizaciones horizontales o verticales de los mismos. Para lograr el entrelazamiento se utilizaron cristales no lineales tipo BBO-II (beta barium borate) que muestran conversión espontánea paramétrica descendente tipo II.
La conversión espontánea paramétrica descendente (SPDC por sus siglas en inglés) es un fenómeno óptico de segundo orden en donde la polarización dipolar depende cuadráticamente del campo eléctrico y fotones incidentes en un cristal no lineal pueden ser “convertidos” en dos fotones 21. Es un efecto importante en óptica cuántica, usado especialmente para producir pares entrelazados de fotones. Un fotón incidente es conocido en SPDC como el “bombeo” mientras que los fotones resultantes son conocidos como “señal” y “testigo”. Se dice que la SPDC es “espontánea” debido a que no hay señal de entrada o campo para estimular el proceso; sino que el par de fotones es generado espontáneamente dentro del cristal. El proceso es “paramétrico” porque depende de los campos eléctricos (y no sólo sus intensidades), implicando que existe una relación de fase entre los campos de entrada y salida. “Conversión descendente” hace referencia al hecho de que los campos señal y testigo siempre tienen frecuencias menores que el bombeo. SPDC puede ser implementada en dos variedades diferentes, caracterizadas por las polarizaciones de la señal y el testigo. Si ambos fotones salientes son polarizados ordinariamente (perpendicular al eje óptico) se le llama conversión de tipo I. Si uno de los fotones es polarizado extraordinariamente (en la dirección del eje óptico) mientras que el otro es ordinario, es llamada de tipo II. En este experimento se explota la birrefringencia del cristal, en este contexto los nombres ordinario y extraordinario se refieren al hecho de que uno de estos rayos cumple con las predicciones de la ley de Snell, mientras que el otro no, como si se tuvieran dos índices de refracción dentro del cristal. Los posibles caminos de los fotones salientes se muestran en la Fig. 1.
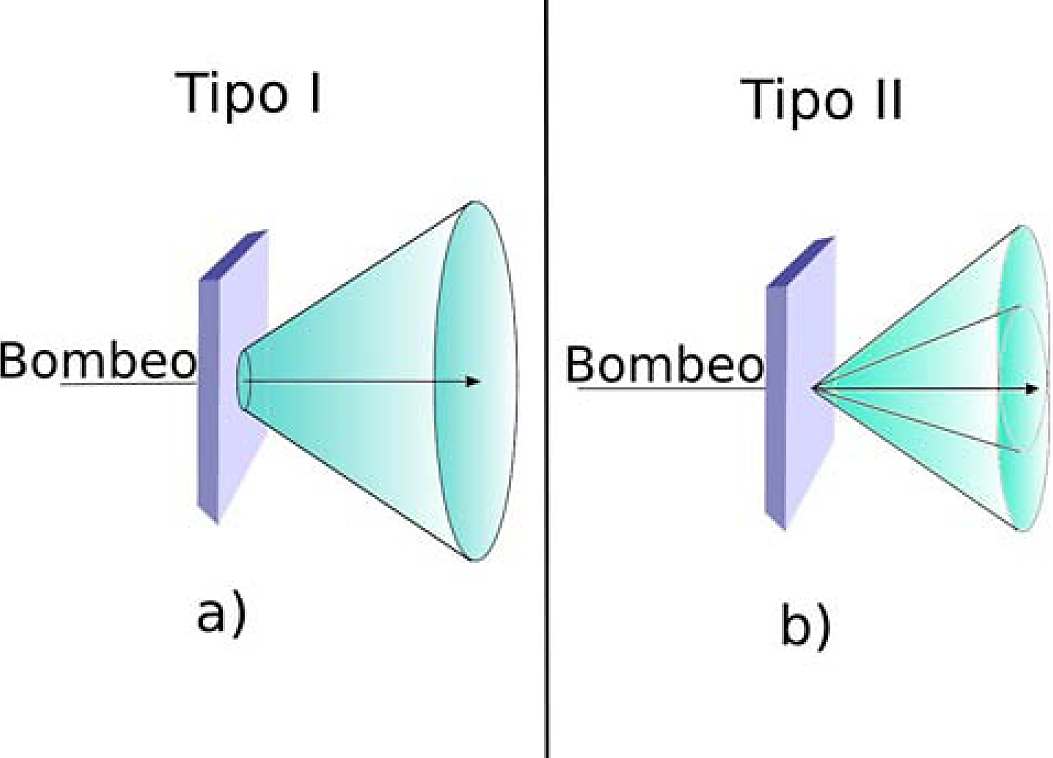
Figura 1 Los dos tipos de conversión paramétrica descendente en un cristal de segundo orden. a) Conversión de tipo I, en donde el haz de bombeo es convertido en dos haces con caminos restringidos a un cono con vértice en el bombeo. b) Conversión de tipo II, en donde el haz de bombeo es convertido en dos haces en lados opuestos del bombeo. Uno de los fotones salientes tendrá polarización ordinaria, mientras que el otro tendrá polarización extraordinaria
En el experimento se utiliza el estado de Bell de la Ec. 3
sin embargo, como se verá en la siguiente sección, con el método que se detalla es posible obtener cualquiera de los cuatro estados de Bell.
3. Montaje experimental
El montaje realizado para crear el par enredado de fotones es similar al utilizado por Kwiat et al. en su artículo de 199518, este se puede ver en la Fig. 2. Además el experimento se basa en el trabajo de Dehlinger y Mitchell de 200219.

Figura 2 Montaje experimental. Láser) diodo láser de 405 nm y 120 mW de potencia. C) cristal no lineal BBO-II, marca Newlight Photonics de 5 × 5 × 2 nm3. C2) cristales compensadores no lineales BBO-II, marca Newlight Photonics de 5 × 5 × 1 nm3. D) diafragmas. P) Polarizadores. APD) Fotodiodos de avalancha, marca Excelitas, con una eficiencia cuántica de 60% para 810 nm.
Se coloca un diodo láser de 405 nm y 120 mW alineado con un cristal no lineal BBO-II marca Newlight Photonics de 5 × 5 × 2 nm3, dentro del cristal se genera un par de fotones, uno de ellos con polarización vertical y el otro horizontal, dado que el par se puede generar en cualquier momento mientras se viaja dentro del cristal se trabaja la suposición de que el número de generaciones como función de la profundidad de rayo en el cristal tiene un perfil gaussiano con su máximo ubicado a mitad del camino entre las dos caras de mayor área del cristal, i.e. se generan pares más frecuentemente a mitad del camino dentro del cristal que en las orillas.
Para lograr el enredamiento es vital que en el lugar de medición puedan existir ambos tipos de polarización. Una conclusión inmediata es que en las intersecciones entre los dos conos es posible que esto ocurra. A lo largo de estas dos direcciones, en donde los conos se traslapan, la luz puede ser descrita esencialmente por el estado entrelazado de la Ec. (4).
en donde H y V indican polarización horizontal (extraordinaria) y vertical (ordinaria), respectivamente. El par de fotones generado dentro del cristal sale en direcciones de ±5 con respecto a la dirección del haz de bombeo. Debido a que es un cristal birrefringente una de las dos componentes de polarización habría tardado más en salir del cristal que la otra, lo cual da como resultado la fase relativa φ.
Para llegar al estado de Bell es necesario eliminar la fase relativa. Usando cristales birrefringentes adicionales es posible modificar el valor de φ a voluntad, en especial en valores de 0 y π, en nuestro caso colocando cristales BBO-II de 5 × 5 × 1 nm3 en el camino de los haces resultantes, haciendo que φ = 0. De la misma forma, una placa retardadora de media onda puede ser utilizada para cambiar una polarización horizontal por vertical y viceversa. De esta manera, uno puede producir fácilmente cualquiera de los cuatro estados de Bell,
En la Fig. 3 se pueden apreciar los dos conos producto de la SPDC. Al salir de los cristales de corrección se cuenta ya con el estado enredado en la zona de traslape de los dos conos. Con el fin de aislar estos rayos se colocan un par de diafragmas que permitan seleccionar tan solo esta zona y depurar lo demás.
El haz que sale del diafragma es entonces mandando a un detector en cada lado, los detectores son fotodiodos de avalancha marca Excelitas con una eficiencia cuántica de 60% para 810 nm, los fotodiodos a su vez se encuentran conectados a una computadora que con ayuda del Software Sistema de coincidencias FCE_BUAP, labVIEW Instrument permite hacer el conteo de coincidencias de forma eficaz y ordenada.
4. Predicciones de teorías de variables ocultas
En una teoría realista de variables ocultas, cada fotón cuanta con una ángulo de polarización λ bien definido, es decir, cuando un fotón pase por un polarizador colocado en un ángulo γ, siempre será registrado como Vγ si λ es más cercano a γ que a γ + π/2, es decir
En cada par generado dentro del cristal el fotón señal y el testigo tienen la misma polarización. A medida que se producen pares de fotones , λ cambia de una manera impredecible que cubre uniformemente el rango de polarizaciones posibles. En este caso λ es una variable oculta, información ausente en la mecánica cuántica. Suponemos que la teoría es local, i.e. los resultados de las mediciones están determinados por características de objetos presentes en el lugar de la medición. Suponemos además una teoría realista en donde todas las cantidades medibles tienen valores definidos, independientemente de nuestro conocimiento o desconocimiento de ellas. Por último, no es necesario que λ varíe de manera aleatoria, sino que puede cambiar en cierta forma determinista que no se ha descubierto. Una teoría con estas características predice que la probabilidad de coincidencia es 19
mientras que la mecánica cuántica predice una probabilidad de coincidencias de 19
en donde los subíndices VV indican el resultado al medir la polarización en α y β respectivamente, en este caso diría que ambos fotones se encuentran verticales con respecto a sus respectivos polarizadores.
La comparación entre estas dos predicciones se puede ver en la Fig. 4

Figura 4 Comparación entre las predicciones para la probabilidad de coincidencias como función del ángulo relativo.
La desigualdad de Bell, en nuestro caso, restringe el grado de correlación entre polarizaciones al medir con distintos ángulos de polarización. Se toman en cuenta dos medidas de correlación, la primera
La medida E(α,β) varía entre 1 y -1, adquiriendo el primer valor cuando la polarización siempre coincide y el segundo cuando pasa lo contrario. La segunda medida es
La importancia del factor S, reside en el hecho de que para cualquier teoría de variables ocultas sus valores se encuentran constreñidos por |S| ≤ 2.. Mientras que utilizando la mecánica cuántica existen ciertas configuraciones que violan dicha desigualdad. Un ejemplo de esto es
para una teoría de variables ocultas, utilizando las Ecs. (6), (8) y (9) se obtiene un valor de S = 2, mientras que utilizando las Ec. (7) en lugar de (6) se predice
5. Resultados y análisis
Las coincidencias obtenidas para cada combinación de ángulos son mostradas en la Tabla I, como se comentó en la sección anterior sólo es necesario medir en ciertas configuraciones para determinar si se viola o no la desigualdad de CHSH, en este caso se utilizaron 16 direcciones notables.
A partir de estos datos se encuentra que
La incertidumbre asociada al parámetro de Bell S se calcula según la Ec. (11),
en donde Ni es la i-ésima medición de cada una de nuestras 16 combinaciones de ángulos.
El hecho de que en este caso se obtenga una S con valor negativo podría entrar en contradicción con uno de los artículos en que este experimento se basa 19, donde se obtiene un valor positivo, sin embargo es vital recordar el hecho de que el estado que se genera en nuestro experimento es
mientras que el usado en el experimento de Dehlinger es
lo cual resuelve nuestro aparente problema en el signo de S.
6. Conclusiones
Se concluye que el teorema de Bell es cierto, dado que se viola la desigualdad de CHSH por un margen amplio. Se obtiene un parámetro con valor absoluto mayor al reportado en el artículo de Dehlinger 19. Se concluye que los estados enredados creados tenían una fidelidad aceptable para fines del presente trabajo, ya que reproducen los valores teóricos predichos. Como resultado de la violación de la desigualdad CHSH es posible concluir que la mecánica cuántica no puede ser una teoría de variables ocultas locales. Concluir que la interpretación ortodoxa es la adecuada, o que los postulados de la realidad y localidad son falsos cae en el terreno de la especulación y es una pregunta más filosófica que científica; sin embargo, hasta el día de hoy, parece ser la interpretación más exitosa de la mecánica cuántica y predice correctamente las correlaciones que se observan experimentalmente, por lo que si bien no se concluye que es cierta la interpretación ortodoxa de la mecánica cuántica sí se puede decir que es altamente confiable. Discusiones al respecto pueden encontrarse en Ref. 1, y 22 a la 24 entre otros. En este experimento se tiene el problema de asumir el muestreo justo, sin embargo se ha reportado en la literatura un experimento que cubre exitosamente los huecos en los experimentos diseñados para violar las desigualdades de Bell 25, concluyendo lo mismo que en este y muchos otros trabajos. Por último se muestra una manera sencilla de crear cualquiera de los cuatro estados de Bell para su utilización en otros experimentos con tecnología al alcance de un laboratorio destinado a estudiantes de licenciatura.











 nueva página del texto (beta)
nueva página del texto (beta)




