PACS: 78.67.Bf; 73.20.Mf; 63.20.Pw; 78.67.-n; 42.25.Bs
1. Introducción
Las nanoestructuras y las nanopartículas se utilizan en la fabricación de sensores biológicos y químicos, en la nanolitografía, en el monitoreo ambiental, en filtros ópticos, en guías de onda y en la medicina. Se han creado nanopartículas con distintas morfologías como anillos, cubos, pirámides y esferas. Recientemente se han usado esferas para realizar componentes nano-ópticos en dos dimensiones.
Para comprender las propiedades ópticas asociada a una partícula de forma esférica y estructuras más complicadas debemos remontarnos al inicio del siglo XX. En aquellos años, G. Mie 1 estudia la difracción de una onda plana electromagnética monocromática por una esfera y encuentra una solución exacta a este problema, en el mismo trabajo aplica la solución al estudio óptico de coloides formado por partículas metálicas. Este trabajo es la base para el entendimiento de la respuesta óptica de las nanopartículas. En el mismo año, P. Debye resolvió un problema similar con el objetivo de encontrar la presión de la luz sobre una esfera e introdujo los llamados potenciales de Debye 2. Anteriormente, J.C. Maxwell-Garnett 3 explicó los colores de vidrios y de coloides metálicos, cuando las partículas metálicas suspendidas son muy pequeñas, usando la teoría de medios inhomogéneos de Lorenz 4.
Posteriormente Stratton 5 en 1941 resume los trabajos más importantes que se habían realizado antes de ese año. Existen dos libros especializados dedicados a la difracción asociada a partículas pequeñas, uno por van de Hults 6 publicado en 1957 (versión mejorada en 1981) y otro de Bohren y Huffman 7 en 1983, que tratan el temas de difracción de luz por esferas, también con otras formas. Otros dos excelentes libros en el tema de “clusters” metálicos son el de Kreibig and Vollmer 8 en 1995 y otro editado por Mishchenko et al.9 en el 2000.
También, en las áreas de la nano-óptica y de las pinzas ópticas se ha estudiado el problema de la difracción de luz por nano y micro-esferas, así como nano-objetos con otras formas. En el campo de la nano-óptica el estudio está dirigido a calcular y/o medir la distribución de campo a distancia de orden de la longitud de onda del objeto difractor. Algunos libros que abordan este problema en la temática del campo cercano son el de Paesler y Moyer 10 publicado en 1996, Ohtsu 11 en 1998, Courjon 12 en 2003, y Novotny y Hetcht 13 en 2006.
Mientras que el campo de las pinza ópticas está centrado en el atrapamiento y manipulación de átomos, moléculas, nano y micro partículas dieléctricas y metálicas, células vivas, así como en la transferencia de momento lineal o momento angular entre un campo electromagnético altamente confinado y las partículas. Así por ejemplo, además de poder atrapar una partícula se ha hecho girar micro partículas esféricas cuando se usa un haz de luz polarizados circularmente. Un muy buen libro sobre este tema es el editado por Ashkin 14 y publicado en 2006.
En síntesis, estudios de nano y micro partículas han sido importantes en áreas como la espectroscopia de coloides, de campo cercano y de fuerzas producidos por campos electromagnéticos. La forma esférica ha sido la piedra angular de esos estudios, ya que se pueden realizar cálculos exactos.
En 1977 Ashkin y Dziedzic 15 observaron resonancias en esferas dieléctricas, atrapadas o levitadas usando láseres, las cuales son llamadas modos de galería susurrantes (Whishpering Gallery Modes WGM por sus siglas en Ingles) y se deben al campo evanescente producido por la reflexión total interna del campo incidente producido en el interior de la esfera.
Un año después, Chýlek et al., al estudiar el mismo sistema, encuentran que a cada resonancia es posible asociarle un coeficiente del desarrollo multipolar del campo esparcido de la solución de Mie, son las llamadas ondas parciales 16.
La búsqueda de resonancias en esferas es amplia, Ruppin en 1970 17 calcula los modos para el caso no-retardado. Englman y Ruppin así como Fuchs y Kliewer, de forma independiente, en 1968 encuentran los modos de una esfera para el caso retardado y aplicados a esferas de materiales iónicos 18,19. Experimentos de absorción en pequeños cristales iónicos (MgO de 0.1 μm) fueron realizados por Genzel and Martin en 1972 20.
Es bien sabido que las frecuencias asociadas a los modos (WGM y PS) dependen del tamaño, la forma, y composición de la partícula, así como del medio en que se encuentra. El símbolo PS usado en el párrafo anterior se refiere a modos denominados plasmones de superficie que son soportados en esferas metálicas. Además, no es necesario usar algún medio de acoplamiento para excitarlos 21. En 1999 usando la teoría FDTD (siglas en Ingles de Diferencias Finitas en el Dominio del tiempo), Shinya y Fukui estudian la interacción de ondas evanescentes con micro esferas dieléctricas y excitan un WGM 22. Napóles et al estudiaron, con el mismo método, los WGM en cilindros 23.
Los nanojets (nano scale photonic structure) son regiones volumétricas de sub-longitud de onda de alta concentración de energía que aparecen a distancias del orden de la longitud de onda de la superficie de micro-esferas dieléctricas. La difracción de haces Gaussianos altamente convergentes difractado por micro esferas dieléctricas fue estudiado recientemente por Devilez et al., 24. Los nanojets producidos por micro esferas a su vez están siendo usados para agrandar la fluorescencia de moléculas individuales colocadas dentro de estas regiones 25.
El desarrollo de este trabajo está hecho de la siguiente manera. En la Sec. 2 se introducen los armónicos esféricos para resolver la ecuación de la onda esférica escalar, se resuelven las ecuaciones de Maxwell mediante un desarrollo multipolar donde se usan los armónicos esféricos vectoriales, comenzando con el desarrollo de una onda plana, para posteriormente estudiar el problema del esparcimiento de la esfera. Se toma la notación del texto Classical Electrodynamics por D. Jackson 26, ya que en el capítulo 10 menciona de forma breve el problema de Mie. Los armónicos esféricos vectoriales son la piedra angular de la expansión multipolar de un campo electromagnético.
Por último, en la Sec. 3 se presentan los resultados numéricos, criterio de convergencia, el campo cercano, la sección de extinción de una esfera dieléctrica. En la Sec. 3.1 se estudia la difracción por esferas dieléctricas, en 3.2 los nanojets y en 3.3 se excita un WGM para las polarizaciones TE y TM. Se puede discutir el caso de las esferas metálicas y la excitación de plasmones de superficie, pero será tema de otro trabajo posterior.
2. Difracción de Ondas Electromagnéticas por esferas
En esta sección se calcula el campo electromagnético de una onda plana difractada por una esfera dieléctrica o metálica, de radio a, suspendida dentro de un medio no absorbente. Para resolver las ecuaciones de Maxwell se utiliza un desarrollo multipolar para representar a los campos, y se divide el espacio en dos regiones, fuera (medio 1) y dentro (medio 2) de la esfera. Los medios se consideran lineales, isotrópicos, no-magnético, y homogéneos. La esfera puede ser dispersiva.
Si se asume que la dependencia temporal de los campos es armónica, es decir,
y
La representación multipolar de los campos está dada por,
donde ε es la constante dieléctrica y μ es la
susceptibilidad magnética,
Donde
2.1. Desarrollo Multipolar de una Onda Plana
En esta parte vamos a delinear como se transforma una onda plana en su representación cartesiana a su representación multipolar.
El campo magnético de la onda electromagnética plana incidente que está oscilando linealmente en la dirección x y que viaja en la dirección z es,
Usando la Ec. 10.45 de la Ref. 26 para el desarrollo en serie de la exponencial, además escribiendo en coordenadas esféricas, el campo magnético (4) puede escribir como
Aplicando el rotacional a (5) y de las ecuaciones de Maxwell se tiene que
dónde Z1 es la impedancia del medio 1 (el medio incidente).
Ahora igualando (1) con (5), multiplicando por
Usando el resultado dado por (A1) y resolviendo la integral se encuentran los coeficientes
Realizando un procedimiento análogo para el campo eléctrico, Ecs. (2), obtenemos
Si ahora sustituimos el campo eléctrico de la Ec. (6) en la Ec. (9), y empleamos el resultado dado por (A2) se encuentran los coeficientes
Finalmente, el desarrollo multipolar del campo incidente es de la forma:
Como se puede observar solo dos coeficientes con m = +1 y m = -1 son distintos de cero, este resultado permite simplificar bastante el problema como se muestra a continuación.
2.2. Teoría de Mie
En esta sección daremos un bosquejo de la denominada teoría de Mie, que es la solución al problema de la difracción de una onda plana por una esfera.
Consideremos una onda electromagnética plana monocromática, cuyo campo eléctrico presenta polarización lineal a lo largo del eje y con dirección de propagación

Figura 1 Una onda plana monocromática linealmente polarizada en la dirección y viajando en la dirección z en un medio con constante dieléctrica ε1 e incidiendo sobre una esfera de radio a de constante dieléctrica ε2. Δ es el plano de esparcimiento que contiene el vector de la onda incidente
En el sistema a estudiar tenemos un campo dentro de la esfera, y fuera de ella se tienen el campo incidente y el es- parcido. Cada uno de los campos debe de cumplir la física del problema: dentro de la esfera los campos no divergen, entonces la función fl (qr) = jl (q2r) es una función Bessel esférica de primera clase de orden l. El campo esparcido se debe comportar como una onda viajera, por lo tanto fl (qr) = hl 1(q1r) debe de ser una función Hankel esférica. A continuación mostramos la forma de los campos para las ondas electromagnéticas en cuestión; los campos dentro de la esfera
Y fuera de la esfera
Debido a la simetría del problema derivado del resultado de la expansión multipolar de la onda plana, se escriben los campos de acuerdo a dicho resultado, es decir se simplifica la dependencia en m.
Las condiciones de frontera que se aplican en la superficie de esfera en r = a, son:
Hay que notar que en esta geometría, las componentes tangenciales de los campos están relacionadas con
Sustituyendo los campos eléctricos (11), (13) y (15) en (17a), realizando el producto escalar con
Sustituyendo los campos magnéticos (12), (14) y (16) en (17b) y realizando el producto escalar con
Al despejar
Donde Ke y K1 son las permitividades magnéticas relativas de la esfera y del medio que la rodea respectivamente.
Sustituyendo los campos magnéticos (12), (14) y (16) en (17b) y realizando el producto escalar del resultado con
Sustituyendo los campos eléctricos (12), (14) y (16) en (18a) y realizando el producto escalar con
Al despejar
Los coeficientes dentro de la esfera son:
Una vez que se han calculado los coeficientes a(s), b(s) y a(e), b(e) se pueden calcular todas la cantidades física deseadas, como el vector de Poynting, el campo cercano etc.
2.3. Secciones Eficaces Total, Esparcida y Absorbida
La sección eficaz de esparcimiento (SEE) total de la esfera6,7, es:
La sección eficaz de absorción es
La sección eficaz de extinción es la suma de las secciones eficaces de esparcimiento y de la absorción
Como lo hemos mencionado anteriormente existen modos que pueden ser WGM o PS para el caso de la esfera, esto se manifiesta en un máximo o máximos en la sección eficaz de esparcimiento. Cuando no hay absorción en la esfera, la sección eficaz de extinción es igual a la sección eficaz de esparcimiento.
3. Resultados Numéricos
En esta sección presentamos resultados numéricos de la difracción de ondas electromagnéticas por esferas dieléctricas débilmente absorbentes y no dispersivas (Sec. 3.1). Los radios fueron variados desde 10 nm hasta 2000 nm.
Cabe aclarar que el libro de Bohren y Huffman 7 tiene un apéndice con un código en FORTRAN, para el caso de una esfera, con el que se puede calcular la sección eficaz de extinción, de esparcimiento, así como la intensidad en la aproximación de campo lejano, pero no se puede calcular el campo cercano.
3.1. Esparcimiento electromagnético en esferas dieléctricas
En esta sección se estudiará el esparcimiento de ondas electromagnéticas por esferas dieléctricas no dispersivas y algunas veces débilmente absorbentes. También se analizará la condición para la excitación del llamado modo susurrante de galería o WGM.
Convergencia de la expansión multipolar
En la Sec. 1 se mostró que el campo eléctrico (magnético) se puede expresar en forma multipolar, donde el índice l puede tomar los valores de 1, 2, hasta infinito, mientras que m varia de -l hasta +l en general. Desde el punto de vista del cálculo, la expansión multipolar es cortada hasta un cierto valor L. Así que la pregunta lógica es ¿cuántos términos necesitamos para que la diferencia entre las mismas cantidades físicas calculadas con L y L + 1 no sea más grande que 1%? Cuando se ha alcanzado este criterio se dice que la solución converge para el valor L. La respuesta a esta pregunta no tiene una respuesta universal, si no que depende fuertemente del radio de la esfera y de la longitud de onda, pero también depende del índice de refracción de la esfera y del medio que la rodea. Una regla gruesa es que radios grandes implican L grandes.
Para ejemplificar lo expuesto sobre la convergencia, estudiaremos la difracción de luz, longitud de onda de 633 nm, por una esfera con un índice de refracción de 1.5, radio 10 nm y rodeada por aire cuyo índice de refracción se puede aproximar a 1.0.
En la Fig. 2 se muestra el campo cercano (el módulo cuadrado de campo eléctrico cerca de la esfera) para cuatro distintos valores de L. a) L = 1, L = 2, b) L = 2, c) L = 3, d) L = 4.

Figura 2 El campo cercano, el modulo cuadrado del campo eléctrico, calculado en el plano z - y para una esfera de 10 nm de radio y de Índice de refacción 1.5 en aire n = 1 a A = 633 nm; para diferentes valores de L: a) L = 1, b) L = 2,c) L = 3 d) L = 4. La onda incidente esta linealmente polarizada y se propaga en la direccion z, mientras que el campo electrico oscila en la direccion y.
De las cuatro imágenes se concluye que la convergencia se alcanza cuando L = 4. Hay otras cantidades físicas que convergen para L menores, por ejemplo la sección eficaz de extinción con L = 1 es suficiente para que la curva converja.
De las imágenes se puede observar una aparente discontinuidad entre el campo eléctrico dentro y fuera de la esfera, pero esto se explica por la sencilla razón de que el módulo cuadrado del campo no es continuo, las cantidades que son continuas son la componente normal de desplazamiento y las componentes tangenciales del campo eléctrico.
El tamaño de la esfera es tan pequeño comparado con la longitud de onda que casi no produce difracción, ya que el color asociado a 1 corresponde al módulo cuadrado de la onda incidente. El campo solo se distorsiona muy cerca de la nano-esfera dieléctrica. Cerca de la esfera el campo tiene un comportamiento dipolar, típico de esfera con radios pequeños.
3.2. Nanojets
Una de las características importante, por su reciente aplicación, de la difracción de luz por esferas dieléctricas de tamaños micrométricos, cuando no existe acoplamiento de modos, es que las esferas actúan como lentes gruesas y pueden enfocar la luz en regiones tridimensionales del orden sub-longitud de onda 23. A este efecto se le llama nanojets (nanoscale photonic jet). En esta parte estudiaremos los nanojets como función del radio de la esfera.
Gracias a este fenómeno se ha tenido un gran avance en formar imágenes a escala de nanómetros (nano-litografía) y en espectroscopia Raman para someter moléculas a intensos campos electromagnéticos 24.
En las Fig. 3 se muestra el campo cercano calculado en el plano z - y para una esfera de 1.5 μm y 2 μm de radio en a) y b) respectivamente; con índice de refracción n2 = 1.5 rodeada de aire n1 = 1.0 a λ = 633nm. Se observa que la esfera confina parte de la luz incidente en una región del espacio muy pequeña y muy cerca de su superficie, es decir, se comporta como una lente gruesa.

Figura 3 Campo cercano calculado en el plano z - y para una esfera de a) 1.5 μm y b) 2.0 μm; con un ´ındice de refracci´on n2 = 1:5 rodeada de aire n1 = 1 a ¸ λ = 633 nm. La convergencia se alcanza en a) y en b) con L = 36.
El máximo de intensidad se encuentra en el eje z, esto se debe a que la onda incidente tiene dirección de propagación z. A medida que aumenta el radio de la esfera la región de máxima intensidad se extiende a lo largo del eje z de 0.32λ en (a) y 0.40λ en (b), a su vez el ancho de la región (eje y) se hace más angosta (de 0.60λ a 0.50λ), aproximadamente.
En el interior de la esfera, se puede apreciar como ésta actúa como un lente divergente en hemisferio inferior y luego como una lente convergente en su parte superior.
En el exterior, se puede apreciar la interferencia entre la onda incidente y la esparcida por la esfera en dirección contraria a la onda incidente. De las gráficas se midieron las distancias entre dos máximos consecutivos y la diferencia entre ellas es del orden de λ/2, pero no es exacto como se debería de esperar, quizás sea debido a la cercanía de la esfera.
En la Fig. 4 se muestra la variación del foco f, que es la distancia del máximo de intensidad, medido desde la superficie de la esfera, como función de a, para λ = 633 nm. Podemos distinguir tres regiones; la primera está debajo de los 1200 nm de radio y se caracteriza porque el máximo está sobre la superficie de la esfera, la segunda región está entre 1300 y 1900 nm, la cual presenta máximo y mínimos, los mínimos aparecen cuando se excita un WGM. La tercera región, para radios mayores que 1900 nm, el foco se empieza a alejar de la superficie de la esfera de manera uniforme.
3.3. Modos de galería susurrantes
Otro característica muy importante es que las esferas dieléctricas pueden soportar modos electromagnéticos de superficie, llamados modos de galería susurrantes (WGM), es decir en este caso la luz queda atrapada cerca de la superficie interior de la esfera, debido al campo cercano producido por la reflexión total interna, provocando que la intensidad del campo electromagnético en la vecindad de la superficie aumente 17.
Los WGM que se acoplan a una onda electromagnética incidente se pueden identificar mediante los máximos que aparecen en la sección eficaz de extinción. Estos modos pueden ser tipo TE o TM, y a éstos se les puede asociar una onda parcial (coeficientes en el desarrollo multipolar). Los modos tipo TE están asociados con las ondas parciales al , a su vez los modos tipo TM están relacionados con las ondas parciales bl.
En la Fig. 5 se muestra la sección eficaz de extinción (SEE) versus la longitud de onda para una esfera dieléctrica de 2 μm de radio, un índice de refracción de 1.5 suspendida en el aire n = 1. Para poder asociar los máximos de la SEE a las ondas parciales se buscan los mínimos del denominador de los coeficientes variando la longitud de onda entre los límites deseados.

Figura 5 La seccion eficaz de extincion con respecto a la longitud de onda, de una esfera 2 μm de radio con índice de refraccion ne = 1.5 en el aire n1 = 1. La longitud de onda de mayor valor encima de uno de los picos corresponde a un modo TE, mientras que la mas pequena a uno TM.
Cuando no hay acoplamiento de modos el campo cercano se comporta como los mostrados en las Figs. 2, ¿Cómo será el comportamiento del campo cercano cuando existe acoplamiento entre la luz y un WGM?
En las Figs. 6 se muestra el campo cercano calculado en los planos a) z - y y b) z - x para una esfera de radio 2μm con índice de refracción de 1.5 en aire n = 1 para a λ = 633.4376. El modo resonante es TE y corresponde al orden (25,1).
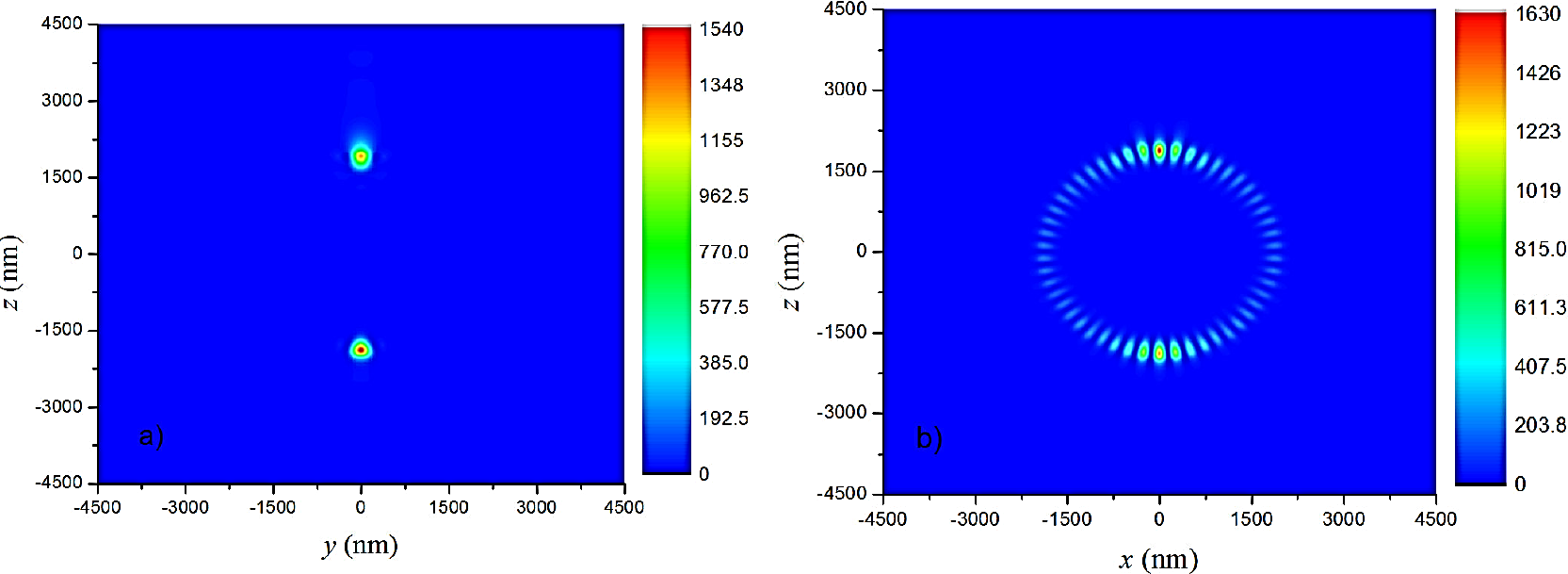
Figura 6 El campo cercano calculado en los planos a) z - y y b) z - x para una esfera de radio 2 μm con índice de refracci´on de 1.5 en aire n1 = 1 para a ¸ λ = 633:4376. El modo es TE y corresponde al onda parcial (25,1). La convergencia se alcanza para L = 36.
En la Fig. 6a) hay dos máximos simétricos con respecto el eje-y y el inferior de mayor intensidad, esto se debe a que el modo oscila en el plano perpendicular a este. En la Fig. 6b) se observan máximos y mínimos de intensidad cerca de la superficie interior de la esfera, lo cual se puede explicar cualitativamente de la siguiente manera, existen dos ondas superficiales en el interior de la esfera una viajando en sentido de las manecillas del reloj y la otra en sentido opuesto, esas dos ondas interfieren provocando el patrón de interferencia descrito.
En las Figs. 7 se muestra el campo cercano calculado en los planos a) z - y y b) z - x para una esfera de radio 2μm con índice de refracción de 1.5 en aire n = 1 para a λ = 619.744. El modo resonante es TM y corresponde al orden (25,1). Se puede apreciar claramente que el fenómeno anterior se invierte, es decir ahora el modo TM oscila en el plano z - y y dentro de la esfera.
4. Conclusiones
En este trabajo estudiamos teóricamente la excitación de modos electromagnéticos en esferas dieléctricas, se observa que existe una región volumétrica, sublongitud de onda, de alta intensidad de campo conocida como nanojet. El foco, que es la distancia a la que se encuentra el máximo de intensidad del nanojet medida desde la superficie de la esfera, presenta valores de orden de la longitud de onda y está a lo largo de la dirección de propagación de la onda incidente. Para una longitud de onda fija se encontró que el foco se aleja de la esfera a medida que aumenta su tamaño a partir de un cierto radio de la esfera.
Por otra parte, se logró excitar los modos WGM TM y TE. En la campo cercano esto modos se propagan a lo largo de la circunferencia y dentro de la esfera, pero confinados en el interior de la misma. El WGM-TM se manifiesta en la plano z - y, mientras que el TE en el plano z - x y el número de oscilaciones que presenta es el doble de la onda parcial asociada.
Cuando se excita un WGM el campo cercano sufre un aumento en intensidad que es 10 veces mayor para el caso TE y TM estudiados, ambos comparado con la intensidad calculada en casos no resonantes.
Las perspectivas a futuro es el estudio de una esfera cerca de una interfaz plana que divide a dos medios semi-infinitos.
El material aquí presentado puede ser útil para estudiantes y/o profesores de nivel universitario avanzado en Licenciaturas de Física o afines o en los inicios de estudios de posgrado en Física, Ingeniera eléctrica, óptica o afines.











 nova página do texto(beta)
nova página do texto(beta)




