Introducción
Entender los patrones de distribución de las especies es uno de los tópicos más importantes de la ecología (Sagarin, Gaines y Gaylord, 2006; VanDerWal, Shoo, Johnson y Williams, 2009). Los patrones de distribución están determinados por factores ecológicos, evolutivos y geográficos, que hacen que el estudio de la distribución de las especies sea un problema complejo (Cain, 1994; Gaston, 2003; Udvary, 1969). Desde el trabajo clásico de Grinnell (1917), se ha considerado que las preferencias ambientales de una especie, denominadas «nicho ecológico», determinan, a través de los parámetros demográficos de cada población, las posibilidades de que una especie colonice exitosamente una localidad. En conjunto con el nicho, parámetros demográficos como la reproducción, la mortalidad y la dispersión, determinan la dinámica metapoblacional y por ende la abundancia y la distribución a diferentes escalas espaciales (Guisan y Thuiller, 2005; Lira-Noriega, Soberón y Milller, 2013; Marion et al., 2012; Schurr et al., 2007; Thuiller et al., 2008).
La forma en la que se relaciona el nicho ecológico con la abundancia es un tema que ha llamado la atención (Siqueira, Bini, Cianciaruso, Oliveira y Trivinho-Strixino, 2009; VanDerWal et al., 2009). En términos generales, se espera que la reproducción y la sobrevivencia sean altas en localidades ubicadas al interior del nicho de una especie y por ende, se alcancen abundancias poblacionales relativamente altas, y lo contrario en localidades periféricas (de Moraes y Viveiros, 2012; Maguire, 1973; Martínez-Meyer, Díaz-Porras, Townsend y Yáñez-Arenas, 2013; Siqueira et al., 2009; VanDerWal et al., 2009). Esta idea fue sugerida por Hutchinson (1957), quien expresa la posibilidad de que exista una región «óptima» dentro del nicho, es decir, con condiciones óptimas para la sobrevivencia de la especie, y regiones con condiciones menos favorables en la periferia. Maguire (1973) es el primero en proponer explícitamente la idea de que diferentes regiones del espacio de nicho corresponden a diferentes valores de la tasa intrínseca de crecimiento y de la abundancia poblacional. Una idea derivada de lo anterior es la hipótesis del «centroide del nicho», la cual plantea que las mayores abundancias se alcanzan en el centro del nicho y conforme una población esté más alejada de este, tenderá a presentar menores abundancias (Martínez-Meyer et al., 2013).
Se ha empezado a acumular evidencia empírica de que la posición de una población en el espacio de nicho determina su abundancia (de Moraes y Viveiros, 2012; Escalante y Martínez-Meyer, 2013; Martínez-Meyer et al., 2013; Siqueira et al., 2009; Torres et al., 2012; VanDerWal, 2009; Yáñez-Arenas, Martínez-Meyer, Mandujano y Rojas-Soto, 2012; Yáñez-Arenas, Guevara, Martínez-Meyer, Mandujano y Lobo, 2014). En estos trabajos se utilizan algoritmos de estimación de nichos para obtener una aproximación al nicho fundamental (medido como «idoneidad de hábitat»), y luego se establece una correlación entre la idoneidad de hábitat con datos de abundancia tomados en campo o de la literatura. Otra forma en la que se ha analizado la relación entre el nicho y la abundancia es identificando el centroide del nicho, calculado a partir de los valores promedio de distintas variables climáticas, y estableciendo una correlación entre la idoneidad de hábitat y la distancia a ese centroide. En ninguno de estos dos casos se incluyen explícitamente procesos poblacionales como natalidad, mortalidad o migración, etc. Por tal motivo, si bien estos procedimientos pueden revelar la existencia de una relación entre abundancia y posición en el espacio de nicho, los resultados son correlaciones que no permiten profundizar en el entendimiento de los mecanismos que determinan esta relación (Dormann, 2009; Pagel y Schurr, 2012).
Se han propuesto diversos métodos para integrar aspectos demográficos en el análisis de los patrones de distribución y abundancia. Los modelos espacio-temporales, por ejemplo, combinan medidas del nicho con parámetros demográficos como la dispersión y el crecimiento poblacional. Se les denomina modelos acoplados o híbridos y pueden dar estimaciones de abundancia en un espacio geográficamente explícito (Catterall, Cook, Marion, Butler y Hulme, 2012; Nenzén, Swab, Keith y Araújo, 2012; Pagel y Schurr, 2012). Estos modelos se han utilizado frecuentemente para estimar la distribución de las especies en escenarios de cambio climático (i.e., Franklin, 2010), y para estudiar la relación entre demografía y la dinámica del área de distribución de algunas especies invasoras (Franklin, 2010; Gallien, Münkemüller, Albert, Boulangeat y Thuiller, 2010; Jongejans et al., 2008; Marion et al., 2012; Pagel y Schurr, 2012; Thuiller et al., 2008).
Trabajos como el de Jongejans et al. (2008) utilizan un modelo híbrido que incluye mecanismos poblacionales y dispersión para estimar la dispersión de una planta, pero sin referencia alguna al concepto de nicho. A su vez, Kearny y Porter (2009) explican cómo los modelos mecanísticos basados en procesos biofísicos ecofisiológicos, se pueden utilizar para estimar la distribución de una especie, pero no muestran cómo relacionarlos con los procesos demográficos y de dispersión. Buckley et al. (2010) proponen un modelo híbrido en el cual la tasa de crecimiento es función del ambiente, sin incluir al proceso de dispersión. La relación entre abundancia y nicho se menciona en un par de líneas, pero no se analiza, y finalmente, Pagel y Schurr (2012) utilizan un modelo híbrido sin estructura de edades para analizar cómo la tasa de crecimiento, la capacidad de carga y la densidad poblacional se relacionan con la probabilidad de presencia de una especie.
El objetivo de este trabajo es analizar la relación entre la abundancia y la posición en el espacio de nicho utilizando un modelo híbrido, que incorpora la estructura de edades de la población y que integra algunos parámetros poblacionales básicos, así como el proceso de dispersión. Con esta aproximación novedosa se pretende contribuir a la teoría que estudia la relación entre abundancia poblacional y la posición en el espacio del nicho, de tal forma que permita profundizar en el entendimiento de los mecanismos que determinan esta relación.
Materiales y métodos
Para estudiar la relación entre la idoneidad del hábitat y las abundancias poblacionales bajo diferentes escenarios de dispersión se utilizó una especie virtual. Se asumió que el nicho fundamental de la especie se mide en términos de la idoneidad del hábitat, la cual está definida por una función f(x, y) donde x y y son las variables ambientales que definen las condiciones donde la especie puede sobrevivir. Se considera que la tasa óptima de reproducción de la especie se obtiene en un cierto punto
En este trabajo se utilizó como función
donde ρ es la correlación entre la variable x y la variable y; μx y μy son las medias de cada una de las variables independientes; σx y σy son las varianzas de ambas. Este método es equivalente a utilizar un método envolvente tipo distancia de Mahalanobis (Farber y Kadmon, 2003).
La función de la ecuación 1 es una función de densidad de probabilidad y por lo tanto esta se reescaló para que sus valores se encuentren en el intervalo cerrado [0,1]. La función de reescalamiento está dada por la expresión:
Dicha función de reescalamiento (ecuación 2) representa la denominada idoneidad del hábitat (Nenzén et al., 2012; Helaouet, Beaugrand y Edwards, 2013), en la que el valor de S(x, y) = 1 ocurre en los niveles de las variables ambientales donde se alcanza la tasa máxima de crecimiento poblacional.
Modelado de la dinámica espacial de crecimiento de la especie
Para analizar la relación entre abundancia poblacional y posición en el espacio de nicho bajo diferentes escenarios de dispersión, se utilizó un modelo híbrido de dinámica discreta de la forma dada por:
donde Nt
+1 es el vector que contiene las abundancias de la población en cada uno de los estadios en las coordenadas (lon,lat) al tiempo t + 1. La matriz M = (ai,j
) es la matriz de proyección poblacional de tipo Lefkovich (Caswell, 2000) y contiene: 1), las proporciones que pasan de un estadio a otro (elementos ai
,
j
con i ≠ j); 2), la proporción de individuos que se mantiene en el mismo estadio (elementos de la diagonal principal) y 3), las fertilidades de los estadios (primer renglón de la matriz). Cada elemento ai
,
j
es una variable aleatoria con una distribución normal N(μi,j,σ). El vector Δ representa el flujo neto de inmigrantes de cada estadio al parche con coordenadas (lon,lat). Con
S(x, y) es una matriz diagonal de n × n dimensiones con las idoneidades de cada estadio (ecuación 5). Las variables x, y dependen de la posición (lon, lat), por lo tanto,
De la estructura del modelo (ecuación 3) se sigue que hay un valor umbral mínimo de idoneidad S 0 por debajo del cual la supervivencia de la especie es nula; es decir, en ausencia de dispersión, si Si (x, y) ≤ S 0 para todo i = 1, ..., n entonces la población en (x, y) tiende a extinguirse debido a que su tasa intrínseca de crecimiento λ será menor a 1. El valor S 0 se calcula como el inverso de la tasa máxima intrínseca de crecimiento
Nótese que el valor máximo de la tasa intrínseca de crecimiento λmax
se alcanza en el valor de idoneidad
Parametrización del modelo híbrido
La matriz M que se utilizará en las simulaciones es la correspondiente a la especie Astragalus scaphoides (tabla 1) tomada de la base de datos demográficos COMPADRE (COMPADRE Plant Matrix Database, 2015). Los estadios son latente, pequeña, grande y reproductiva. Para la dispersión se considerarán dos kernels de dispersión que indican el flujo neto de inmigrantes (esto corresponde al término Δ de las ecuaciones 3 y 4). El primer kernel se refiere a una dispersión a celdas cercanas (kernel SDD) y el segundo a la dispersión a celdas lejanas (kernel LDD). El porcentaje de la población de un parche que se dispersa a los parches contiguos SDD, lo denotamos con α y la que se dispersa a los más lejanos LDD, lo denotamos con β. Se considera que la dispersión ocurre solo en el estadio de semilla. El kernel SDD se da entre las 8 celdas contiguas a cada parche, con una proporción de 0.2α colonizadores hacia cada una de las 4 celdas laterales y una proporción de 0.05α hacia cada celda diagonal (fig. 1a). La dispersión a celdas no contiguas está determinada por un kernel (LDD) de dispersión exponencial del tipo siguiente:
donde Dmax es la distancia máxima a la que puede viajar un individuo y P(d) es la fracción de migrantes que viajan a una distancia d. La proporción máxima de la población que se desplaza está determinada por a. La razón entre c y b define que tan grande es la proporción de individuos que se desplazan a una distancia d. Los valores de los parámetros elegidos fueron a = 0.8, b = 0.8, c = 0.1 y D = 2. La distribución del kernel dados estos parámetros se muestra en la figura 1.
Tabla 1 Matriz de proyección poblacional de Astragalus scaphoides (NR=no reproductiva).
| Latente | Pequeña (NR) | Grande (NR) | Reproductiva | |
|---|---|---|---|---|
| Latente | 0.50 | 0.03 | 0.04 | 5.00 |
| Pequeña (NR) | 0.40 | 0.45 | 0.04 | 0.00 |
| Grande (NR) | 0.00 | 0.24 | 0.37 | 0.16 |
| Reproductiva | 0.10 | 0.06 | 0.52 | 0.80 |

Figura 1 Kerneles de dispersión. Imagen izquierda, dispersión a las celdas contiguas (SDD). Imagen derecha, dispersión a celdas distantes (LDD) como función de la distancia d al parche inicial S.
Para definir el nicho fundamental de la especie virtual, se eligieron como variables ambientales la temperatura media anual y la precipitación en el mes más húmedo, por ser las más importantes para el desarrollo y supervivencia de varias especies (Bartlein, Prentice y Webb III, 1986; Woodward, 1987). Para analizar el proceso de dispersión se eligió como «espacio geográfico» una zona al noroeste de México. En este espacio la especie virtual inicia el proceso de dispersión, y se definió tomando como base el nicho de la especie, es decir los sitios del espacio geográfico donde la especie puede subsistir. Los valores de temperatura media anual (bio1) y de precipitación en el mes más húmedo (bio13) fueron obtenidos de la página de Worldclim (Hijmans, Cameron, Parra, Jones y Jarvis, 2005) a una resolución de 30 segundos de arco. Aquí suponemos que la tasa óptima de reproducción de la especie virtual se alcanza en las medias (μx , μy ) de bio1 y bio13 en el espacio geográfico, los cuales fueron 24.2 °C y 260 mm (este es el centroide del nicho). La correlación de las variables nichos fue de ρ = −0.77 con una desviación de σt = 3.89 para la bio1 y σP = 9.85 para bio13. El valor de la tasa máxima intríseca de crecimiento (λmax ) de la matriz M en condiciones de idoneidad máxima S(μx,μy )=1 es de λmax = 1.6
Utilizando la función rasterToPoints del paquete «raster» de R (Hijmans, 2015), se extrajeron los valores de bio1 y bio13 para el espacio geográfico en cuestión, y se aplicaron las ecuaciones (1) y (2) para obtener la idoneidad S(x, y) en cada una de las celdas (fig. 2). Se eligieron aleatoriamente 10 celdas cuya idoneidad del hábitat fuera mayor al valor de S 0 (en este caso S 0 = 0.625). En estas celdas se colocaron las poblaciones iniciales de la especie virtual y constituyeron el área inicial de distribución (puntos negros en el espacio geográfico, fig. 3).
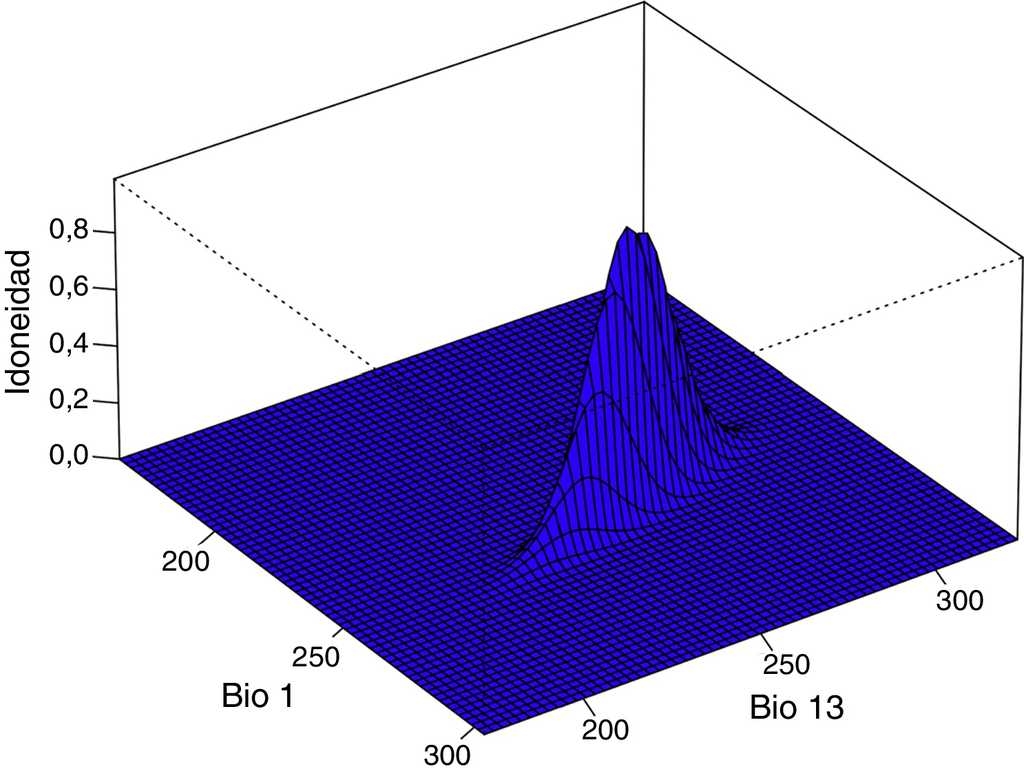
Figura 2 Nicho fundamental de la especie virtual. La función de distribución f(x, y) que se utilizó para definir al nicho fundamental de la especie virtual, fue la función multinormal bivariada; se eligió como variable x a la temperatura media anual (bio1) y como variable y a la precipitación en el mes más húmedo (bio13).

Figura 3 Mapa de idoneidad del hábitat. Los puntos negros muestran los sitios donde se colocaron a las 10 poblaciones iniciales de la especie virtual.
Los escenarios
Se puso a prueba la hipótesis del centroide del nicho (la mayor abundancia se encuentran más cercanos al centroide del nicho) bajo distintos escenarios de dispersión: a) sin dispersión de la especie, i.e. α = 0 = β; b) con dispersión; se simularon un total de 36 escenarios de dispersión, los cuales son resultado de combinar diferentes proporciones de α y β. Los valores posibles de α y β son [0.01, 0.04, 0.06, 0.8, 0.11, 0.14]. Para realizar las simulaciones se utilizó el paquete demoniche de R (Nenzén et al., 2012).
Se realizaron regresiones lineales entre el índice de idoneidad y la abundancia poblacional, usando los coeficientes de determinación. La comparación de las r 2 permitió comparar los resultados entre los diferentes escenarios de dispersión.
Resultados
Modelo sin dispersión
Las mayores abundancias se encontraron en los valores de idoneidad de hábitat S cercanos al óptimo de la especie (i.e. centroide del nicho). La correlación r fue positiva y la r 2 fue de 0.95 (fig. 4). La variación no explicada se debe a la estocasticidad introducida en los parámetros demográficos del modelo.
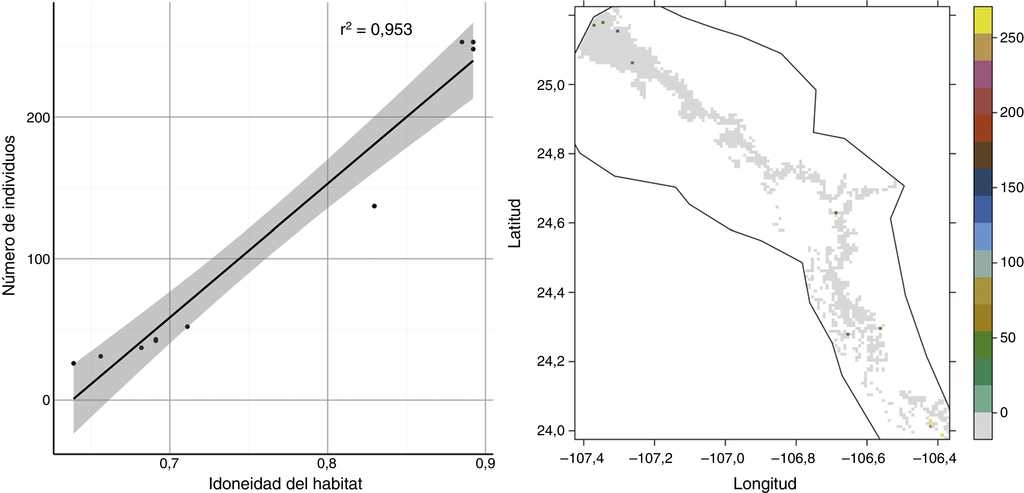
Figura 4 Relación entre idoneidad del hábitat y la abundancia para el escenario donde no hay dispersión. Imagen izquierda, la correlación entre estas variables fue de r2 =0.95, la banda alrededor de la línea de tendencia representa el intervalo de confianza de la estimación a un nivel de confianza del 95%. Imagen derecha, proyección de las abundancias en el espacio geográfico.
Modelo con dispersión
En general, los valores que tomó la abundancia fueron más altos conforme la proporción de individuos con dispersión a celdas cercanas SDD fue mayor. Por ejemplo, el número máximo de individuos que alcanzó un parche en el escenario LDD = 0.01 SDD = 0.01 fue de 3,500 individuos, mientras que en el escenario de mayor dispersión (LDD = 0.01 SDD = 0.08 fue de 120,000 individuos (fig. 5).
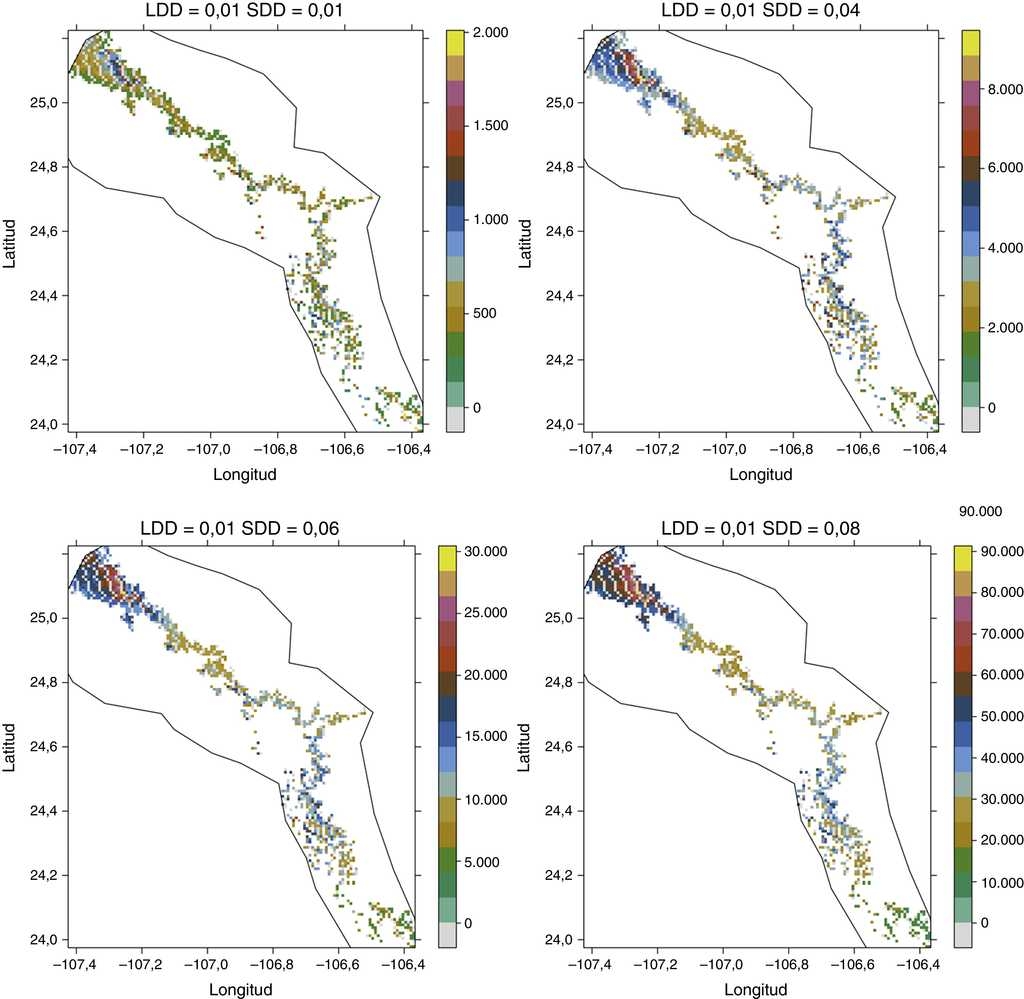
Figura 5 Proyección al espacio geográfico de las abundancias poblacionales para diferentes escenarios de dispersión a cortas distancias SDD (0.01≤α≤0.08) y valores de dispersión a largas distancias LDD fijos (β=0.01).
La relación idoneidad del hábitat S y abundancia fue positiva para todos los escenarios. Sin embargo, se observó que conforme incrementó la proporción de α individuos que viajaban a distancias cortas (SDD), los coeficientes de determinación r 2 resultaron considerablemente más bajos (fig. 6). En estos escenarios, conforme incrementó la dispersión, la relación entre abundancia e idoneidad se hace más débil, por lo tanto fue posible encontrar abundancias altas en sitios con idoneidad baja (fig. 6).
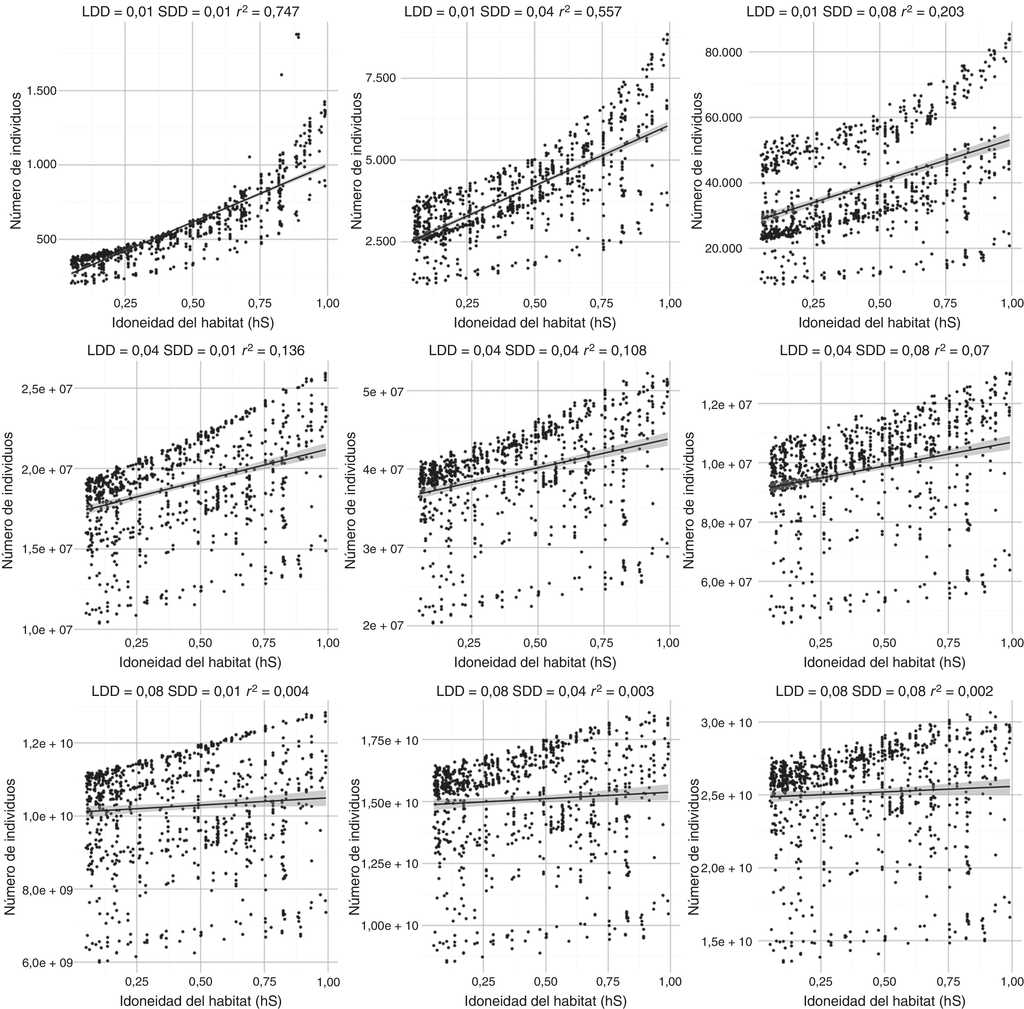
Figura 6 Correlaciones entre idoneidad del hábitat y las abundancias poblacionales para diferentes escenarios de dispersión a cortas distancias SDD y a largas distancias LDD. La banda alrededor de las líneas de tendencia representa el intervalo de confianza de la estimación a un nivel de confianza del 95%.
Las relaciones que se encontraron entre la idoneidad del hábitat y la abundancia poblacional para el escenario donde la proporción de individuos susceptibles a dispersarse a las largas distancias es de 0.01 ≤ β = 0.06, con proporciones de 0.01 ≤ α ≤ 0.14 individuos susceptibles dispersarse a cortas distancias, muestran una correlación r positiva en todos los casos, sin embargo también muestran que tanto r como r 2 disminuyen al incrementar las proporciones α y β (fig. 6).
En términos generales las r 2 obtenidas en las simulaciones para todos los escenarios de dispersión disminuyeron conforme se incrementaron las proporciones de individuos con dispersión a celdas cercanas SDD (α) y de individuos dispersión a celdas no contiguas LDD (β) (fig. 7).
Discusión
En este trabajo analizamos la relación entre la abundancia de una especie virtual y su posición en el espacio de nicho, utilizando un modelo «híbrido» con estructura de edades que integra procesos demográficos y de dispersión. A pesar de que en la literatura hay trabajos en los que se utilizan modelos híbridos y mecanicistas para estudiar la distribución y abundancia de las especies, la diferencia principal radica en que el nuestro integra diferentes escenarios de dispersión.
El principal resultado que encontramos es que existe una correlación positiva entre abundancia poblacional y la idoneidad de hábitat, es decir, se confirma la hipótesis del centroide del nicho. Otro resultado fundamental es que esta correlación está regulada por la relación que guardan los parámetros demográficos respecto a los de la dispersión.
Los resultados obtenidos muestran que la intensidad de la correlación positiva entre abundancia e idoneidad del hábitat depende de la capacidad de dispersión de la especie en cuestión: la correlación entre abundancia e idoneidad del hábitat es casi perfecta en un escenario de no dispersión; sin embargo, cuando se incluye el factor dispersión, la correlación declina abruptamente pudiéndose encontrar poblaciones con abundancias mayores en sitios donde la calidad del hábitat es baja. Este resultado concuerda con lo señalado por Pulliam (2000), quien afirmó que las especies frecuentemente se encuentran en sitios donde su tasa de crecimiento es negativa (Pulliam, 2000; Schurr et al., 2012). A este fenómeno se le ha denominado dinámica fuente-sumidero (Pagel y Schurr, 2012; Pulliam, 1988, 2000; Schurr et al., 2012) y depende en gran medida de si las respuestas densodependientes afectan la dinámica de dispersión de la especie.
Nuestros resultados refuerzan las predicciones teóricas informales derivadas de la teoría del nicho de Hutchinson (Maguire, 1973; Schurr et al., 2012) y da elementos teóricos a los resultados empíricos como los de VanDerWal et al. (2009), Escalante y Martínez-Meyer (2013) y Martínez-Meyer et al. (2013), ya que dan una explicación plausible en términos poblacionales a las correlaciones que se obtienen entre abundancia y distancia en el espacio de nicho. Además, sugieren algunas hipótesis acerca de las condiciones en las que los procesos demográficos y de dispersión pueden hacer que la correlación entre abundancia y distancia al centroide del nicho sea baja, por ejemplo, se espera que las especies cuyas tasas de migración son altas, muestren una correlación baja entre su abundancia y su nicho.
Asimismo, nuestro trabajo complementa estudios como el de Holt, Lawton, Gaston y Blanchette (1997) en el que se analiza la relación entre la abundancia y el rango de distribución de la especie. A diferencia del enfoque de Holt et al., que se basa en la idea de que el proceso de dispersión de la especie ha concluido y no consideran el efecto de la migración-inmigración sobre las abundancias locales, nosotros mostramos cómo el proceso de dispersión y el nicho pueden determinar la abundancia de las poblaciones en el rango geográfico.
Finalmente, si bien el enfoque de los modelos híbridos es prometedor, existe una limitante práctica para incluir el término de dispersión de estos modelos, ya que la estimación de los kernels de dispersión es difícil, los datos son escasos y kerneles con colas largas son matemáticamente difíciles de manejar (Barve et al., 2011). A pesar de que en este trabajo se enfatizó el papel de la dispersión en la relación entre abundancia y posición en el espacio de nicho, otra limitante importante para la comprensión de esta relación son las interacciones, de manera que la ecuación de abundancia de una especie en un espacio geográficamente explícito debe ser una función de su nicho fundamental, su capacidad de dispersión y las interacciones que tenga con las demás especies (Soberón, 2010). El trabajo que presentamos aquí pretende ser una base teórica sobre la cual avanzar incluyendo este otro tipo de factores, lo cual permitirá entender mejor la compleja red de factores que determinan la geometría y la estructura interna del área de distribución de una especie.











 nova página do texto(beta)
nova página do texto(beta)



