Introduction
Based on the usefulness of internuclear energy potential function that describes the
molecular structure, there has been a radical interest devoted to the determination
of energy spectrum of diatomic molecules. The potential function involves usually
consists of three spectroscopic parameters. Using the spectroscopic parameters,
several authors have studied different molecules under different energy potential
models in terms of vibration transitional frequency and validated their results by
comparing it with the experimental data [1-8]. Depending on the potential
function and the molecule to be studied, some calculated results fairly agreed with
the experimental values while others are in good agreement with the experimental
values. In ref. [1], the authors obtained the
average absolute deviation of Morse potential function for
where
Simplifying the above equation along with potential (1) gives
Following the value of the screening parameter above, the potential parameters are
given as
Bound State Solutions
The Schrὅdinger equation for a quantum system with a non-relativistic energy E and an interacting potential V(r,θ,φ) coupled with a reduced mass μ is given by
Where
where v is the vibrational quantum number and j is the rotational quantum number. In order to obtain the analytical solutions of Eq. (5) for any arbitrary j - state, one must approximate the centrifugal term when α<<1 Several approximation schemes were developed to deal with the centrifugal term [9, 10]. In this study, we employ an improved Greene-Aldrich approximation scheme [11] to get rid of the centrifugal term.
The constant in Eq. (6) is a dimensionless constant with numerical value as 1/12 that is obtained using the following power series
If the constant
where we have used the following for mathematical simplicity
Having obtained Eq. (8), we now employ
the basic concept and formalism of the supersymmetric approach to solve the
Schrὅdinger-like equation given in Eq.
(8). On the basis of the formalism of supersymmetric approach, the ground
state wave function
where
For compatibility of the property of both the left hand side and the right hand side of Eq. (11), the superpotential function can be put forward in the following form
where
Using the formalism of supersymmetric approach, the construction of the partner
potentials is significant as these give the choice of mapping function for the
derivation of recurrence relations. Hence, using Eq. (12), it becomes very easy to construct a pair of
supersymmetric partner potentials
Eq. (16) and Eq. (17) are connected via a simple
formula/relation that satisfied the partner potentials
where
The integral limits are two turning points that are determined by the equation. Following the concept and formalism of supersymmetric approach and the standard WKB method [17, 18], the exact energy spectra of the shape invariance potential can be determined. Considering Eq. (12) and Eq. (13), the supersymmetric WKB quantization condition shown in Eq. (19) can now be written as
Defining a transformation of the form
The turning points in Eq. (21) are given by
Solving Eq. (21), the term
where we have used integral of the form
for evaluation. Using Eq. (8) and Eq. (17), we have the following equation
Plugging Eq. (24) into Eq. (26), the ro-vibrational energy equation for a system interacting with a molecular attractive potential is obtained as
If we consider
The Radial Wave Function
To obtain the radial wave function, we define
Analyzing the asymptotic behaviour of Eq.
(30) at origin and at infinity, it can be tested that when
Consider a trial wave function of the form
Eq. (35) is a differential equation satisfied by hypergeometric function. Hence, its solution is obtain via
Replacing the function
Discussion
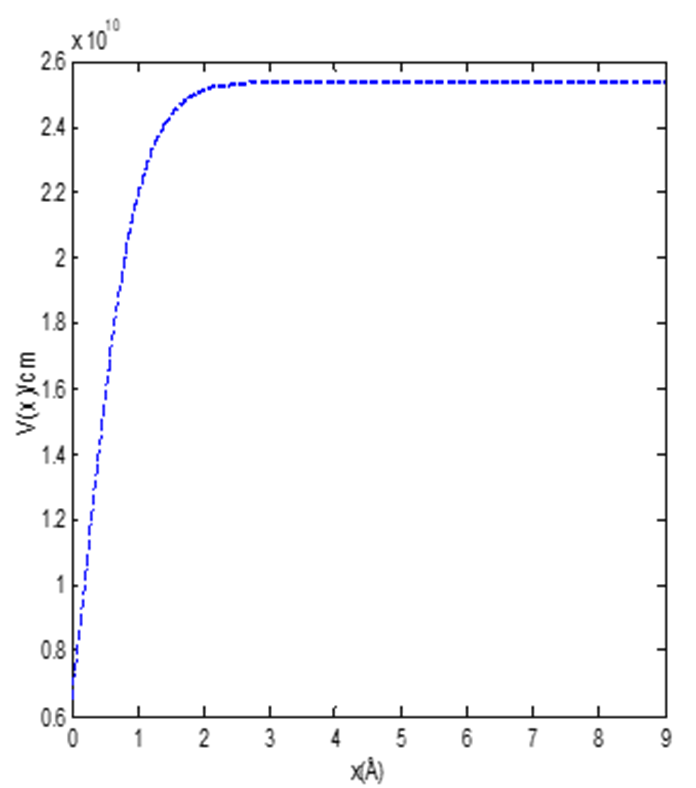
The shape of the molecular attractive potential for chlorine molecule is shown in Fig. 1. The effect of the screening parameter on the energy of the attractive potential is shown in Fig. 2. The energy varies directly with the screening parameter. However, as the screening parameter increases above 2, the energy of the system has turning point starting from the energy of the highest quantum state. In Fig. 3, we examined the effect of the dissociation energy on the energy of the molecular attractive potential. The energy of the system increases monotonically as the dissociation energy increases gradually for all the quantum states. Figures 2 and 3 are plotted using Eq. (29)
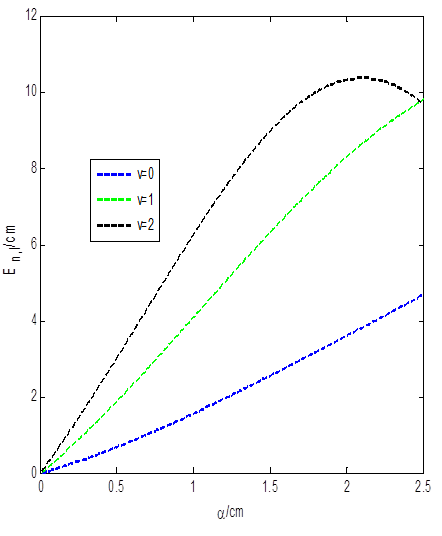
Fig. 2 Variation of energy against the screening parameter for molecular
attractive potential with
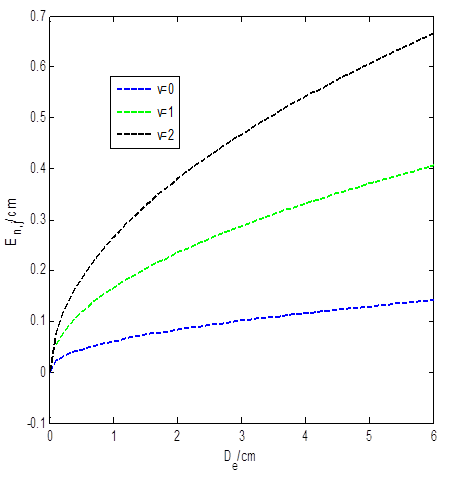
Fig. 3 Variation of energy against the screening parameter for molecular
attractive potential (a) and improved Rosen-Morse potential (b) with
The comparison of the present results and the previous results for attractive
molecular potential are presented in Table 1.
The present results and the previous results agreed with one another. Imputing the
experimental data
Table 1 Comparison of the energy of the attractive molecular potential for
various quantum states and angular quantum states with
| n |
|
|
|
|---|---|---|---|
| 0 | 0 | 3.977598260 3.977598297 | 6.798286894 6.798287056 |
| 1 | 0 1 |
4.809523564 4.792524933 4.940728412 4.955213995 |
9.108667476 9.075571808 9.543813181 9.592230252 |
| 2 | 0 1 2 |
4.976039762 4.967085778 5.003831145 4.999752546 5.012890620 4.980612046 |
9.723414912 9.696564702 9.872914437 9.882375036 9.966101890 9.981247750 |
| 3 | 0 1 2 3 |
4.998604183 4.999955612 4.988391768 4.980876842 4.973213572 4.926380148 4.962051470 4.844354168 |
9.936060172 9.920455196 9.987095855 9.984079176 10.01504929 9.998356127 10.02737409 9.962890521 |
| 4 | 0 1 2 3 4 |
4.963711498 4.975269344 4.931818281 4.926609948 4.899233943 4.847057320 4.874254153 4.744069524 4.858672822 4.620971626 |
9.997844943 9.993868287 10.00275060 9.997542268 9.994948650 9.962692496 9.982639903 9.891525886 9.972505733 9.791084240 |
Table 2 Comparison of the observed values and calculated values of the Chlorine molecule (Cl2)
| v | RKR (cm-1) [19] | calculated results | |
|---|---|---|---|
| j=0 | j=1 | ||
| 0 1 2 3 4 5 6 7 8 9 10 |
279.15 833.43 1382.33 1925.79 2463.80 2996.28 3523.40 4044.80 4560.50 5070.50 5574.70 |
272.0144 815.8936 1359.5343 1902.9364 2446.0997 2989.0242 3531.7099 4074.1566 4616.3643 5158.3328 5700.0622 |
272.4928 816.3721 1360.0128 1903.4150 2446.5783 2989.5029 3532.1887 4074.6354 4616.8432 5158.8118 5700.5412 |
where,
Conclusion
The solution of the radial Schrödinger equation was obtained under the attractive molecular potential model. It was observed that two different energy equations can be obtained under this potential. Then, one of the energy equations obtained was used to generate numerical values for chlorine molecule which perfectly agreed with the experimental values. The deviation of the calculated values from the experimental values is approximately 0.0589 % for j = 0 and 0.0603 % for j = 1 Thus, the attractive molecular potential perfectly fits the computation for Chlorine molecule.











 nueva página del texto (beta)
nueva página del texto (beta)