Article

 

Substituent and Solvent Effects on the Electronic and Structural Properties of Silacyclopropylidenoids

 

Cem Burak Yildiz,^1,2 and Akin Azizoglu^1,*

 

¹ Laboratory of Computational Chemistry, Department of Chemistry, Faculty of Arts and Sciences, University of Balikesir, Balikesir, Turkey. azizoglu@balikesir.edu.tr

² Department of Chemistry, Faculty of Arts and Sciences, University of Aksaray, Aksaray, Turkey.

 

Received December 19^th, 2013
Accepted September 30^th, 2014

 

Abstract

The isomeric structures, energies, and properties of the substituted silacyclopropylidenoids, SiC₂H₃RLiBr (R = -H, -CH₃, -SiH₃, -CN, -OH, -NH₂), were studied by ab initio calculations at the MP2/6-311+G(d,p) level of theory. The calculations indicate that each of SiC₂H₃RLiBrs has three stationary structures: silacyclopropylidenoid (S), tetrahedral (T1 or T2), and inverted (I). The conductor-like polarizable continuum model (CPCM) using various solvents (dimethyl sulfoxide, acetone, tetrahydrofuran, and diethyl ether) has been applied to compute single point energies for title molecules. In addition, the molecular electrostatic potential maps, natural bond orbitals, and the frontier molecular orbitals of substituted silacyclopropylidenoids were calculated.

Key words: Silacyclopropylidene; ab initio; MP2; Reactive Intermediate.

 

Resumen

Las estructuras isoméricas, energías y propiedades de los silaciclopropilidenoides, SiC₂H₃RLiBr (R = -H, -CH₃, -SiH₃, -CN, -OH, NH₂), fueron estudiados mediante cálculos ab initio al nivel MP2/6-311+G(d,p). Los cálculos indican que cada uno de los SiC2H3RLiBrs posee tres estructuras estacionarias: silaciclopropilidenoide (S), tetraédrica (T1 o T2), e invertida (I). El modelo continuo polarizable similar a conductor usando varios disolventes (DMSO, acetona, tetrahidrofurano y éter dimetílico) fue aplicado para calcular las energías de un solo punto para las moléculas. Además, se calcularon los mapas del potencial electrostático molecular, los orbitales de unión natural, y los orbitales moleculares frontera de los silaciclopropilidenoides substituidos.

Palabras clave: Silaciclopropilideno; ab initio; MP2; reactivo intermedio.

 

Introduction

Silylenoids (R₂SiXM, X = halogen, M = alkali metal), are important intermediates in organic and silicon chemistry [1-4]. In few decades, the synthesis and chemistry of silylenoids have attracted considerable attention from the viewpoints of both applied and theoretical chemistry. In principle, once formed silylenoids can react by dimerization, insertion, and cycloaddition and otherwise just as silylene would do, and the preparation of silylenoid is difficult [2-4]. Clark et al. [5] have carried out the first theoretical study on the simplest silylenoid H₂SiLiF, and then many different types of silylenoids have been systematically investigated [6-8]. The unsaturated silylenoids have also been studied well [9,10].

The silacyclopropylidenoids, silicon analogue of cyclopropylidenoids, are compounds in which Li and Br are bound to the same silicon atom, and have been predicted to be active intermediates in organosilicon reactions [11,12]. Contrast to extensive experimental and computational works on cyclopropylidenoids [13-16], only a few scientific studies on silacyclopropylidenoids have been reported so far [17-19]. More recently, the ab initio calculations at the Hartree-Fock and MP2 levels for SiC₂H₄MX (X = F, Cl, Br, and M = Li, Na) have been carried out to investigate several properties of silacyclopropylidenoids, silylenoidal (S), inverted (I), and tetrahedral (T) (Scheme 1). It is concluded that LiF and NaF units for silacyclopropylidenoids increase the configurational stability of the T and I forms, respectively. However, the S form has lower energy than the I and T forms for LiCl, LiBr, NaCl, and NaBr. Computed energy differences between S, I, and T forms range from 0.70 to 8.70 kcal/mol at the MP2/6311+G(d,p) level [19].

To our knowledge, there have been no other theoretical calculations for the solvent and substituent effects on the isomeric structures of silacyclopropylidenoids. Hence we wish to investigate the isomeric structures, energies, and the properties of substituted silacyclopropylidenoids, SiC₂H₃RLiBr (where R = -H, -CH₃, -SiH₃, -CN, -OH, -NH₂) in both gas and solvent phases. The substituents have been located at appropriate position to enhance the stability of the isomeric structures. To determine the influence of solvent on the stability of studied molecules, we have also performed single point energy calculations with the help of CPCM method in dimethyl sulfoxide, acetone, diethyl ether, and tetrahydrofurane. The calculated highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), and the molecular electrostatic potential maps (MEP) of title compounds also describe the molecular electronic properties in detail.

 

Computational details

The geometry optimization and vibrational frequencies of the silacyclopropylidenoids for each forms (S, I, and T (T1 or T2)) were achieved in the gas phase using Møller-Plesset perturbation theory (MP2) with the 6-311+G(d,p) basis set [20]. The harmonic vibrational frequency computations were used to confirm that the optimized structures were minima, as characterized by the positive vibrational frequencies. The corresponding harmonic vibrational frequencies were calculated with the help of Gaussian03 package program [21]. The optimized geometries at the MP2/6-311+G(d,p) were used to calculate the single point energies in dimethyl sulfoxide (ε = 46.7), acetone (ε = 21.0), tetrahydrofurane (ε = 7.5), and diethyl ether (4.3) solvents at the same level by employing CPCM method [22-24]. The frontier molecular orbitals (FMOs) and molecular electrostatic potential maps (MEPs) were also calculated at the MP2/6-311+G(d,p) level of theory. The optimized structures were visualized with the help of GaussView 3.0 program [25]. In our previous study silacyclopropylidene, SiC₂H₄, was considered as singlet because its singlet-triplet gap was calculated to be 42.9 kcal/mol at the B3LYP/6-31G(d) level [17]. The singlet and triplet forms of substituted silacyclopropylidenoids are also examined in this study.

 

Results and Discussion

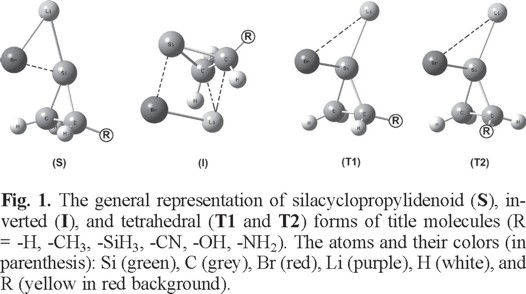
At first the singlet and triplet states of silacyclopropylidenes, SiC₂H₃R (where R = -H, -CH₃, -SiH₃, -OH, -NH₂, and -CN) were analyzed at the MP2/6-311+G(d,p) level of theory. However, triplet state of SiC₂H₃R (R = -NH₂) could not be optimized on its potential energy surface. For other substituents, the singlet states are calculated to be of lower energy than the triplet ones by 42.2 kcal/mol (for -H), 40.6 kcal/mol (for -CH₃), 44.2 kcal/mol (for -SiH₃), 40.4 kcal/mol (for -OH), and 46.0 kcal/mol (for -CN) (Table S26). Like silacyclopropylidenes [17], the singlet is also determined to be the ground-state for substituted silacyclopropylidenoids. Then, we have examined the possible geometries of substituted (R = -H, -CH₃, -SiH₃, -CN, -OH, -NH₂) silacyclopropylidenoids, which can be regarded as a complex formed by free silacyclopropylidene and LiBr. The position of substituent has been considered in two different sides: the substituent may locate either on the same side of the Br atom or opposite side of the Br atom. In both cases, the position of substituent determines the stability of structures. The substituent is placed on the opposite side of Br atom for of silylenoidal (S), inverted (I), and tetrahedral (T1) isomers to form most stable configuration (Fig. 1). Especially, tetrahedral (T1) forms with the -OH, -CN, and -NH₂ substituents could not be optimized at the MP2/6-311+G(d,p) level. For this reason, we calculated the T2 isomer for the substituents (-OH, -CN, and -NH2) which are positioned on the same side of the Br atom (Fig. 1). In the inverted geometry, the Li atom is positioned between the C₁ and C₂ atoms. The Li atom of the I form interacts strongly with the C₁ and C₂ atoms (Fig. 1). Moreover, the Br atom shows only non-bonding interactions with the Si atom in silacyclopropylidene units. However, the Li and Br atoms interact with the Si atom in the silylenoidal (S) and tetrahedral (T1)/(T2) forms (Fig. 1).

Tables S1-S3, presented in Supplementary material, give us a chance to compare bond lengths of title molecules with the reference bond lengths of H₃Si-Br (2.229 Å), H₃Si-Li (2.479 Å), and Li-Br (2.187 Å), H₃C-SiH₃ (1.876 Å) at MP2/6-311+G(d,p) level of theory. It is clear from the results that the most elongated Si-C₂ bond is appeared in the I form of -CN with 2.003 Å as compared to reference bond length of H₃Si-CH₃ (1.876 Å) at MP2/6-311+G(d,p) theory (Table S1). The Si-C₂ bond length of the I form for -CN is significantly higher than that of S, I, and T1/T2 forms, in the range of 0.034-0.111 Å. The theoretical results also indicate that the bond distance of Li-Br raises with the increase of LiSiBr bond angle in the T1 and T2 isomers (Table S2). For the -NH₂ substituted structures, the Li-Br bond of the I form increases slightly as compared to reference Li-Br bond (2.187 Å). In contrast, the most strongly elongated LiBr bond distance is determined to be in the -SiH₃ substituted T1 geometry. Moreover, the Si-Li bond length is shortened in the S, T1 and T2 isomers. However, the bond length alternation is increased in the I forms, especially for -CN with 3.120 Å.

Moreover, the calculated C₁SiC₂ bond angle of the T1(-H, -CH₃, -SiH₃)/T2(-OH) forms is higher than that of I and S forms (Tables S1-S3). When compared to the C₁SiC₂ bond angle of title compounds, the smallest one is found to be the I form (-NH₂) with 44.2^°. On the other hand, the largest one is determined to be the S form with the substituent of -SiH₃ at the MP2/6-311+G(d,p) level of theory. When compared to the SiLiBr bond angles of S geometries, the smallest one is found to be 62.5^° for the -CN, whereas the largest one is determined to be 64.4^° for -NH₂ at the MP2/6-311+G(d,p) level of theory (Table S3).

The direct bonding interaction between neighboring atoms, provided by the Wiberg bond orders (WBO) as well, is generally associated with the electron density between two relevant atoms [26-28]. The WBO values of title molecules at the MP2/6311+G(d,p) level of theory are tabulated in Tables S4-S6. A WBO value is directly proportional to the strength of covalent bonding interactions between neighboring atoms. For instance, a large WBO value reflects a strong covalent bonding interaction between two relevant nuclei. The results depict that the Si-Li bond of the I form for each substituent has an ionic rather than covalent nature due to the estimated WBO values which are in the range of 0.016 and 0.021 (Table S4). In contrast, the Si-Br bond of the I, S, and T1/T2 forms has a substantial covalent character because of the high WBO values (in the range of 0.468-0.848, Tables S4-S6). Furthermore, the C₁-C₂ and C₂-R bonds have strong covalent bond interactions within the studied structures due to the high bond order values (in the range of 0.756 and 1.088). However, it seems almost certain that there is no covalent bond interaction between the Li and Br atoms in the T1 and T2 forms because of extremely low WBO values (in the range of 0.019 - 0.021, Table S5).

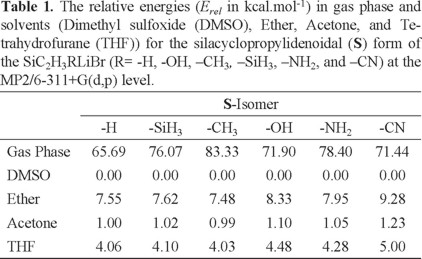
In addition, we have performed conductor-like polarizable continuum model (CPCM) calculations [22-24] to examine the solvent effect on the stability of substituted silacyclopropylidenoids by using dimethyl sulfoxide (DMSO), diethyl ether, acetone, and tetrahydrofurane (THF) as a solvent. The single point energy calculations in selected solvents at the MP2/6-311+G(d,p) level were then performed for all optimized structures in gas phase. The obtained energy results are presented at Tables S7-S9 in the supplementary material. The S forms of SiC₂H₃RLiBr (R = -H, -OH, -CH₃, -SiH₃, -NH₂, and -CN) are energetically more stable than the I and T1/T2 forms in gas phase. On the other hand, the T1 isomers with -H, -CH₃, -SiH₃ and T2 with -OH, -NH₂, -CN substituents are energetically less stable than the corresponding I ones by 7.66 kcal/mol, 7.40 kcal/mol, 6.49 kcal/mol, and 9.85 kcal/mol, 9.46 kcal/mol, 5.64 kcal/mol in gas phase, respectively. The relative energies (E_rel) in gas phase and solvents for S, I, and T1/T2 forms of the SiC₂H₃RLiBr (R = -H, -OH, -CH₃, -SiH₃, -NH₂, and -CN) are also computed and summarized at Tables 1, 2, and 3. It can easily be seen that the solvation stabilizes all the studied species. The stability of the S, I, and T1/T2 forms is increased by increasing the dielectric constant (ε) of solvent. In other words, title structures are more strongly stabilized in DMSO than in others. From the calculated energy values, the S form of R = -CH₃ in DMSO is more stable, by 1.0 kcal/mol, 4.03 kcal/mol, and 7.48 kcal/mol than in acetone, THF, and diethyl ether, respectively (Table 1). The S form (R = -H) is determined to be higher energy than the T1 form (R = -H) by 3.87 kcal/mol, 3.46 kcal/mol, 2.21 kcal/mol, and 0.78 kcal/mol in DMSO, acetone, THF, and diethyl ether, respectively (Tablas 1-3)(2).

NBO (Natural Bond Orbital) analyses have an appealing aspect of highlighting the individual bonds and lone-pairs energy that play an important role in the chemical processes [27,28]. A useful feature of the NBO method is that it describes interactions in both filled and virtual orbital spaces that could enhance the analysis of intra- and inter-molecular interactions. In NBO analysis, large stabilization energy value, called as E(2), shows the intensive interaction between electron-donors and electron-acceptors, and greater the extent of conjugation of the whole system. The large stabilization energy value, called as E(2), is calculated as described previously, using the equation,

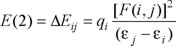
where q_i is the donor orbital occupancy, ε_i and ε_j are diagonal elements (orbital energies) and F(i,j) is the off-diagonal NBO Fock matrix element.

The intra-molecular interactions are mainly formed by the orbital overlap between bonding (BD)Si-Li and anti-bonding (BD*)Si-Br bond orbitals in the T1 and T2 forms. These interactions result in intra-molecular charge transfer causing stabilization of the systems by 19.40 kcal/mol, 22.24 kcal/mol, 24.00 kcal/mol, 24.26 kcal/mol, 24.33 kcal/mol, and 24.85 kcal/mol for R = -CN, -SiH₃, -OH, -NH₂, -CH₃, and -H, respectively. The interaction of bonding (BD)C₁-C₂→ anti-lone pair (LP*)Li is the most important factor contributing to stability of the I forms with 10.50 kcal/mol, 9.07 kcal/mol, and 9.36 kcal/mol for R = -H, -CH₃, and -SiH₃, respectively. On the other hand, the NBO analysis clearly manifests the evidence of the intra-molecular charge transfer from (BD)C₂-Si, (LP)N, and (LP)O to anti-bonding orbitals of C₂-H, and C₂-H in the I forms for -CN, -NH₂, and -OH, respectively. These interactions stabilize the I forms of -CN, -NH₂, and -OH substituents by 21.97 kcal/mol, 13.82 kcal/mol, and 12.20 kcal/mol, respectively. Furthermore, the strongest delocalization of the S form involves the interaction of the lone pair (LP)Br with the anti-lone pair (LP*)Li except for -CN substituent. From the NBO calculations of the S forms, the (LP)Br → (LP*)Li interactions are stabilized by the energies of 60.09 kcal/mol, 60.59 kcal/mol, 60.98 kcal/mol, 61.20 kcal/mol, 55.31 kcal/mol, and 61.41 kcal/mol for -OH, -SiH₃, -CH₃, -CN, -NH₂, and -H, respectively (see supplementary material, Table S10-S25, available online).

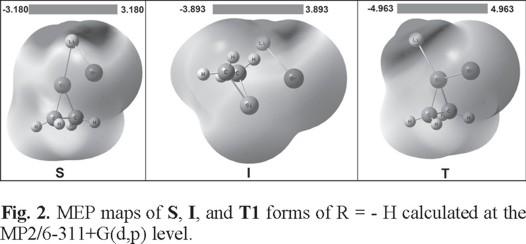
The MEP is used widely as an index of the charge distribution within a molecule. Visualization of MEP is a good way for understanding molecular reactivity, intermolecular interactions, molecular recognition, electrophilic reactions, and a variety of chemical phenomena [29-33]. The 3D plots of MEPs of title compounds calculated from MP2/6-311+G(d,p) level for the S, I and T1 forms of unsubstituted structure (R = -H, Fig. 2). The Fig. 2 describes the electrostatic potentials at the surfaces which are represented by different colors for the mentioned compounds. The negative (red and yellow) and the positive (blue) regions in the MEP were related to the electrophilic and nucleophilic reactivity, respectively. As can be seen in Fig. 2, the negative region of title structures is localized on the Si and Br atoms, whereas the positive region is observed around the Li atoms for the silylenoidal (S), inverted (I), and tetrahedral (T1) forms for R = -H. These sites give information concerning the region from where the compound may have metallic bonding and intermolecular interactions.

Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO) are very effective parameters to describe structural properties [34-40]. Surfaces for the frontier orbitals were drawn to understand the bonding scheme of structures. The energy of the HOMO is directly related to the ionization potential, and that of LUMO is directly related to the electron affinity. The HOMO-LUMO energy gaps also give us a chance to determine chemical reactivity and kinetic stability of molecules. Having a small frontier orbital gap, a molecule is more polarizable and generally associated with a high chemical reactivity, low kinetic stability and also called as soft molecule. The plots of FMOs can be seen in Fig. 3. In the HOMO, the charge density is mainly accumulated on the SiC₂H₃R ring of the S, I, and T1/T2 isomers, whereas in the case of the LUMO, more charge density moves to the Li atom. In consequence, SiC₂H₃R part of title structures, considered as a free silylene, show nucleophilic character.

The I form of -CN substituent has the highest HOMO-LUMO energy gap with 0.319 eV. However, the lowest one is determined as 0.263 eV in the T2 form of -OH substituent. The small energy gap means low excitation energies for many of the excited states and low chemical hardness for T2 form of -OH. Quantitative data also indicate that SiC₂H₃R parts of studied molecules have largest contribution to HOMO and hence the effect of electron donating/withdrawing groups in silacyclopropylidenoids affect significant changes in the HOMO level.

 

Conclusions

The structural and electronic properties of the substituted silacyclopropylidenoids have been studied in detail. Counter ion (Li⁺) attacks to the Si of the silacyclopropylidene unit in different positions to form the S, I, and T1/T2 as local minima on their PES. The S, I, and T1 T2 isomers of silacyclopropylidenoids were calculated at the MP2/6-311+G(d,p) level. All substituents stated on the opposite side of the Br atom to optimize most stable structures except for the T2 forms for -CN, -NH₂, and -OH. In the T2 forms, the substituents located on the same side of Br atoms. Theoretical WBO values indicate that the Li-Br bond of the I, S, T1/T2 forms have ionic character rather than covalent nature due to the calculated low WBO values which are in the range of 0.012 and 0.307. Furthermore, the C₂-R bond of the I, S, and T1/T2 forms is the strongest bond having a substantial covalent character with the WBO value between 1.088 and 1.089. The theoretical results prove that the S forms are energetically the most stable ones in the gas phase. For the present analysis, Conductor-like polarizable continuum model (CPCM) was used to gauge the stability of title compounds in different solvents (Dimethyl sulfoxide, Acetone, Diethyl ether, and Tetrahydrofurane). From CPCM results, the T1 and T2 forms are found to be most stable ones in DMSO. It can be concluded from NBO analysis that the strongest delocalization in the silylenoidal (S) forms involves the interaction of the lone pair (LP)Br with the anti-lone pair (LP*)Li for all the calculated molecules at the MP2/6-311+G(d,p) level.

 

Acknowledgements

The authors would like to acknowledge the financial support from the Scientific and Technological Research Council of Turkey (TUBITAK KBAG-212T049). Furthermore, we are grateful to the referees for their helpful suggestions.

 

References

1. Tamao, K.; Kawachi, A. Angew. Chem. Int. Ed. Engl. 1995, 34, 818-820.         [ Links ]

2. Pietschnig, R. J. Chem. Soc. Chem. Commun. 2004, 2004, 546-547.         [ Links ]

3. Molev, G.; Zhivotovskii, D. B.; Karni, M.; Tumanskii, B.; Botoshansky, M.; Apeloig, Y. J. Am. Chem. Soc. 2006, 128, 2784-2785.         [ Links ]

4. Cho, H. M.; Lim, Y. M.; Lee, B. W.; Park, S. J.; Lee, M. E. J. Organomet. Chem. 2011, 696, 2665-2668.         [ Links ]

5. Clark, T.; Schleyer, P. v. R. J. Organomet. Chem. 1980, 191, 347-353.         [ Links ]

6. Feng, S.; Feng, D.; Deng, C. Chem. Phys. Lett. 1993, 214, 97-102.         [ Links ]

7. Flock, M.; Marschner, C. Chem. Eur. J. 2005, 11, 4635-4642.         [ Links ]

8. Qi, Y.; Chen, Z.; Li, P. Comput. Theory Chem. 2012, 969, 61-65.         [ Links ]

9. Feng, S.; Feng, D.; Li, M.; Bu, Y. Chem. Phys. Lett. 2001, 339, 103-109.         [ Links ]

10. Feng, S. Y.; Feng, D. C.; Li, M. J. Int. J. Quant. Chem. 2002, 87, 360-365.         [ Links ]

11. Sigal, N.; Apeloig, Y. J. Organomet. Chem. 2001, 636, 148-156.         [ Links ]

12. Escudie, J.; Ranaivonjatovo, H.; Bouslikhane, M.; Harouch, Y. E.; Baiget, L.; Nemes, G.C. Russ. Chem. Bull. Int. Ed. 2004, 53, 1020-1033.         [ Links ]

13. Fedorynski, M. Chem. Rev. 2003, 103, 1099-1132.         [ Links ]

14. Azizoglu, A.; Ozen, R.; Hokelek, T.; Balci, M. J. Org. Chem. 2004, 69, 1202-1206.         [ Links ]

15. Azizoglu, A.; Balci, M.; Mieusset, J-L.; Brinker, U. H. J. Org. Chem. 2008, 73, 8182-8188.         [ Links ]

16. Kilbas, B.; Azizoglu, A.; Balci, M. J. Org. Chem. 2009, 74, 7075-7083.         [ Links ]

17. Azizoglu, A.; Yildiz, C. B. Organometallics 2010, 29, 6739-6743.         [ Links ]

18. Azizoglu, A.; Yildiz, C. B. J. Organomet. Chem. 2012, 715, 19-25.         [ Links ]

19. Yildiz, C. B.; Azizoglu, A. Struct. Chem. 2012, 33, 1777-1784.         [ Links ]

20. Hehre, W. J.; Radom, L.; Schleyer, P. v. R.; Pople, J. A. Ab Initio Molecular Orbital Theory; John Wiley & Sons: New York, 1986.         [ Links ]

21. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J. A.; Jr.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A. Gaussian 03. Revision C02 ed.; Gaussian, Inc., Pittsburgh PA, 2003.         [ Links ]

22. Barone, V.; Cossi, M. J. Phys. Chem. A. 1998, 102, 1995-2001.         [ Links ]

23. Cossi, M.; Barone, V. J. Chem. Phys. 2001, 115, 4708-4717        [ Links ]

24. Barone, V.; Cossi, M.; Rega, N.; Scalmani, G. J. Comput. Chem. 2003, 24, 669-681.         [ Links ]

25. Dennington, R.; Keith, T.; Millam, J.; Eppinnett, K.; Hovell, W. L.; Gilliland, R. GaussView. Version 3.0; Semichem, Inc., Shawnee Mission, KS, 2003.         [ Links ]

26. Wiberg, K. B. Tetrahedron 1968, 24, 1083-1096.         [ Links ]

27. Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Rev. 1988, 88, 899-926.         [ Links ]

28. Reed, A. E.; Schleyer, P. v. R. J. Am. Chem. Soc. 1990, 112, 1434-1445.         [ Links ]

29. Politzer, P.; Abrahmsen, L.; Sjoberg, P. J. Am. Chem. Soc. 1984, 106, 855-860.         [ Links ]

30. Jovanovski, G.; Cahil, A.; Grupce, O.; Pejov, L. J. Mol. Struct. 2006, 784, 7-17.         [ Links ]

31. Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Comput. Theory Chem. 2012, 991, 124-133.         [ Links ]

32. Yildiz, C. B.; Azizoglu, A. Comput. Theory Chem. 2013, 1023, 24-28.         [ Links ]

33. Kassaee, M. Z.; Najafi, Z.; Shakib, F. A.; Momeni, M. R. J. Organomet. Chem. 2011, 696, 2059-2064.         [ Links ]

34. Fleming, I. Frontier Orbitals and Organic Chemical Reactions; John Wiley & Sons: London, 1976.         [ Links ]

35. Cabrera-Trujillo, J.M.; Robles, J. Phys. Rev. B, 2001, 64, 165408.         [ Links ]

36. Azizoglu, A. Struct. Chem. 2003, 14, 575-580.         [ Links ]

37. Ugras, H. I.; Cakir, U.; Azizoglu, A.; Kılıc, T.; Erk, C. J. Incl. Phenom. Macrocycl. Chem. 2006, 55, 159-165.         [ Links ]

38. Aparicio, F.; Garza, J.; Galván, M. J. Mex. Chem. Soc. 2012, 56, 338-345.         [ Links ]

39. Mendoza-Huizar, L.M.; Rodríguez, D.E.G.; Rios-Reyes, C.H.; Alatorre-Ordaz, A. J. Mex. Chem. Soc. 2012, 56, 302-310.         [ Links ]

40. Ghiasi, R.; Boshak, A. J. Mex. Chem. Soc. 2013, 57, 8-15.         [ Links ]