Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Journal of the Mexican Chemical Society
versión impresa ISSN 1870-249X
J. Mex. Chem. Soc vol.58 no.4 Ciudad de México oct./dic. 2014
Article
A Theoretical Study of Chemical Reactivity of Tartrazine Through DFT Reactivity Descriptors
Luis Humberto Mendoza-Huizar
Universidad Autónoma del Estado de Hidalgo. Área Académica de Química. Carretera Pachuca-Tulancingo km. 4.5 Mineral de la Reforma, Hidalgo, México. hhuizar@uaeh.edu.mx
Received April 8th, 2014
Accepted June 17th, 2014.
Abstract
In this work we have calculated global and local DFT reactivity descriptors for tartrazine at B3LYP/6-311++G (2d,2p) level. Global reactivity descriptors such as ionization energy, molecular hardness, electrophilicity, and total energies were calculated to evaluate the tartrazine reactivity in aqueous and gas conditions. Local reactivity was evaluated through the Fukui function. The influence of the solvent was taken into account with the PCM model. The results indicate that the solvation process modifies the reactivity descriptors values. From our results, it was found that an electrophilic attack allows a direct cleavage of the N=N bond. If a nucleophilic attack is considered as initial attack, it is necessary a second attack by free radicals or electrophiles to cleave the N=N bond. In the case of an initial attack by free radicals, tartrazine requires a subsequent nucleophilic attack to cleave the N=N bond.
Keywords: tartrazine, reactivity, Fukui, B3LYP, PCM.
Resumen
En este trabajo se han calculado descriptores globales y locales de reactividad TFD para la tartrazina en el nivel B3LYP/6-311++G (2d,2p). Los descriptores globales de reactividad tales como energía de ionización, dureza, electrofilicidad y energías totales se calcularon para evaluar la reac-tividad de la tartrazina en medio gaseoso y acuoso. La reactividad a nivel local se evalúo a través de la Función Fukui. La influencia del solvente se tomó en cuenta mediante el modelo PCM. Los resultados indican que el proceso de solvatación modifica los valores de los descriptores de reactividad. A partir de nuestros resultados, se encontró que un ataque electrofílico permite una ruptura directa del enlace N=N. Si se considera inicialmente un ataque nucleofílico, entonces es necesario un segundo ataque mediante radicales libres o electrofilos para romper el enlace N=N. En el caso de un ataque inicial por radicales libres, se requiere un subsecuente ataque nucleofílico para lograr la ruptura del enlace N=N.
Palabras clave: tartrazina, reactividad, Fukui, B3LYP, PCM.
Introduction
Azo compounds (ACs) are intensely colored substances because azo bond (N=N) allows the conjugation of two aromatic rings forming an extensive delocalized system of alpha electrons; causing absorption of light in the visible region (intense yellow, orange, red, blue and even green) [1]. These ACs have been used in large amounts as dyes because they may be obtained from relatively inexpensive methods. In these ACs, it is well known that polar functional groups as -SO3Na, -OH, -COOH and NH2 allow the adhesion of the molecule on the surface of polar fibers [1].
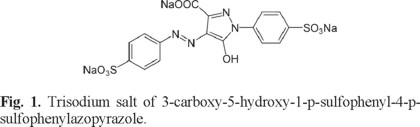
Trisodium salt of 3-carboxy-5-hydroxy-1-p-sulfophenyl-4-p-sulfophenylazopyrazole or tartrazine, see Figure 1, is one of the alimentary synthetic azo dyes most used in the world because it is cheaper than beta carotene [2-5]. Also, tartrazine has been used industrially in the fabrication of drugs, especially shells of medicinal capsules, syrups and cosmetics [6]. This fact and its water soluble nature have caused that tartrazine is considered as a persistent contaminant in industrial effluents [6]. Here, it is important to mention that the presence of dyes as tartrazine in wastewaters reduces the photosynthetic activity causing ecological problems to aquatic ecosystems [7, 8]. Moreover, tartrazine has been associated with allergic reactions [3, 4], hyperactivity [10], behavioral problems [11, asthma [12, 13], migraines, thyroid cancer, among other ills [14]. Therefore, a number of techniques to remove tartrazine from wastewaters are being developed. Physicochemical methods include adsorption [15], electrocoagulation [16, 17], photocatalysis [18, 19], chemical oxidation and reduction [20], electrochemical treatment [21], ion pair extraction [22] while biological methods involve aerobic microorganisms. [23]. Physicochemical methods have several shortcomings such as high cost, limited applicability and/or generation of chemical sludge that presents a disposal problem. Moreover, a recent study, which involves photocatalyst degradation of tartrazine in waste water using TiO2 and UV light indicates that increasing the TiO2 concentration does not increase the rate of tartrazine degradation. Also, a very minor effect has been noted in its degradation process due to the temperature variation [19]. In the case of water-soluble azo reactive dyes, they are resistant to biodegradation and hence conventional aerobic treatment methods cannot be employed [24]. Last results suggest that some methods focused to degrade tartrazine must be improved in order to be applied at industrial level. In this sense, an evaluation of the reactivity exhibited by tartrazine at the molecular level may become fundamental to develop new and better methods to degrade tartrazine in aqueous conditions. Thus, a good knowledge about the reactivity exhibited for tartrazine should be worth in order to develop new degradation methods specifically for this food color dye. Nowadays, the analysis of the reactivity at the molecular level is complicated because the experimental complexity and cost involved. However, the accepted theories of the quantum chemistry provide advantages to analyze the reactivity of molecules. These studies have shown to be reliable and coincident with the experimental behavior [25]. Tartrazine has been scarcely studied from a theoretical point of view [26, 27]. Peica et al studied tartrazine from both experimental and theoretical point of views [26]. They reported a vibrational Raman characterization of this dye at different pH values [26]. On the other hand, Shahir et al analyzed the interaction of tartrazine with some cationic conventional and gemini surfactants [27]. However, to our knowledge, a determination of the global and local reactivity descriptors of tartrazine is still missing. We consider that this kind of study will contribute to get a better understanding about the chemical behavior of this emergent water contaminant.
Theory
Within the framework of the Density Functional Theory, it is possible to define global reactivity parameters which give information about the general behavior of a molecule. These are the electronic chemical potential (μ), the electronegativity (χ), hardness (η) and softness (S) which are defined as [28-30]:
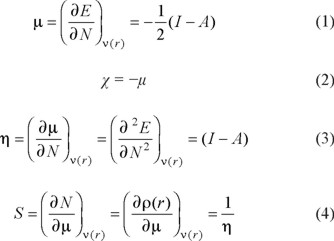
In these equations, E, N, and ν(r) are the energy, number of electrons and the external potential of the system, respectively. It is important to mention that each one of these parameters has a physical meaning. Thus, the chemical potential measures the escaping tendency of an electron and is minus the Mulliken electronegativity [31], while η is related to the polarizability [32, 33]. Additional to µ, χ, η and S, the global electrophilicity index ω was introduced by Parr [34] and it can be calculated by using μ and η:

According to this definition ω measures the susceptibility of chemical species to accept electrons. Thus, low values of ω suggest a good nucleophile while higher values indicate the presence of a good electrophile.
Also, it is important to mention that apart from the global reactivity parameters, it is possible to define local reactivity parameters which can be used to analyze the reactivity on different sites within a molecule. In this sense, the Hard and Soft Acids and Base principle (HSAB) has been useful to predict the reactivity of chemical systems [28, 35-41]. Thus, from HSAB principle and the Density Functional Theory, it has been possible to identify many useful and important reactivity concepts as the Fukui Function 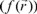 [ 42, 43]. The Fukui function can be written as [28]:
[ 42, 43]. The Fukui function can be written as [28]:
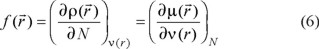
where 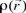 is the electronic density. Gázquez and Méndez demonstrated that sites in chemical species with the largest values of
is the electronic density. Gázquez and Méndez demonstrated that sites in chemical species with the largest values of 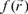 are those with higher reactivity [42, 43]. The condensed form of the Fukui function for an atom k in a molecule can be expressed as:
are those with higher reactivity [42, 43]. The condensed form of the Fukui function for an atom k in a molecule can be expressed as:
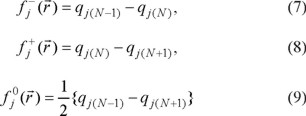
for an electrophilic 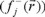 , nucleophilic
, nucleophilic 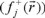 or free radical attack
or free radical attack 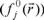 on the reference molecule, respectively. In these equations, qj is the atomic charge at the jth atomic site in the neutral (N), anionic (N+1) or cationic (N-1) chemical species.
on the reference molecule, respectively. In these equations, qj is the atomic charge at the jth atomic site in the neutral (N), anionic (N+1) or cationic (N-1) chemical species.
Results and Discussion
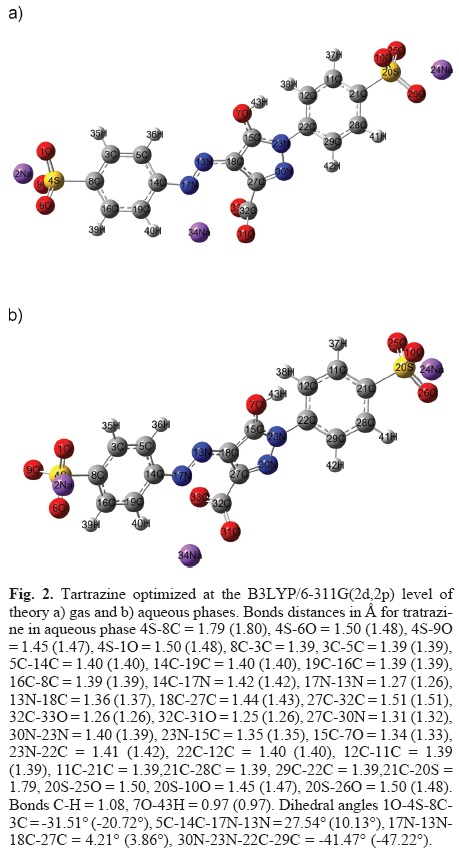
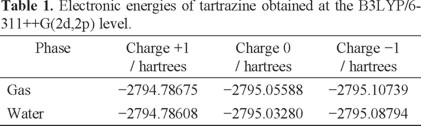
Figure 2a shows the optimized structure of tartrazine at B3LYP/6-311++G (2d,2p) level in the gas phase. The total energy calculated was -2795.05587778 hartrees. In order to analyze the effect of water on the electronic properties of tartrazine, the optimized structure in the gas phase was reoptimized at the B3LYP/6-311++G(2d,2p) level without any symmetry constraints employing the PCM solvation model. In this model, the solvent is treated as an unstructured continuum characterized only by its dielectric constant which is 78.5 for water at 25 °C. The optimized structure, in aqueous phase, is depicted in Figure 2b. The total energy for tartrazine calculated under this condition was -2795.03280003 hartrees. The energy difference between the gas phase and the structure in aqueous phase is 14.48 kcal mol-1 which corresponds to the solvation energy of tartrazine. It is important to mention that were not obtained significant differences, neither in distances nor angles, when the solvent effect was considered. Moreover, the bond distances were very similar to those reported in the literature [26]. A frequency analysis was applied to the optimized geometries to verify the stability criterion, in all cases the frequency values were positive and its values were coincident with those reported in the literature [26].
Global Reactivity Descriptors
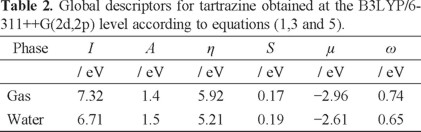
Global Reactivity descriptors were obtained at the level of theory B3LYP/6-311++G(2d,2p). Table 1 reports the values of the electronic energies calculated for tartrazine with the charges +1, 0 and -1, which correspond to the cationic, neutral and anionic species, respectively. The energy values of the ionic states of tartrazine, cation and anion, were calculated by using the geometry of the neutral system. From the values reported in this table, it was possible to calculate the energy value of the vertical electronic affinity as A = E(N) - E(N + 1) where E(N) and E(N + 1) are the total ground-state energies in the neutral N and singly charged (N + 1) configurations. In a similar way, the ionization potential was calculated as I = E(N - 1) - E(N). The values of μ, η, ω were calculated employing the equations 1, 3 and 5 respectively (see Table 2). From the results reported in Table 2, it may be observed that the global hardness of tartrazine decreases when solvent was taken into account. This result suggests that tartrazine stability diminishes in the aqueous phase. Also, note that μ is lower in the gas phase in comparison to the aqueous phase. This behavior indicates that tartrazine is more electronegative in the gas phase. Moreover, the value of ω is bigger in the gas phase in comparison to the aqueous phase, this fact would suggest that nucleophilic behavior increases on tartrazine in the presence of water. However, it is important to remember that the solvation may change the value of ω relative to gas phase. One of the reasons for this situation is that a polar solvent like water might stabilize charged species relative to the gas phase, and this would cause an increment in the value of ω without having a direct implication on tartrazine reactivity. Thus, it is necessary to highlight that an analysis of chemical reactivity of tartrazine based only on ω values is not definitive. Therefore, a combined analysis of global reactivity descriptors is necessary to identify changes on tartrazine reactivity in the aqueous phase.
Local reactivity descriptors
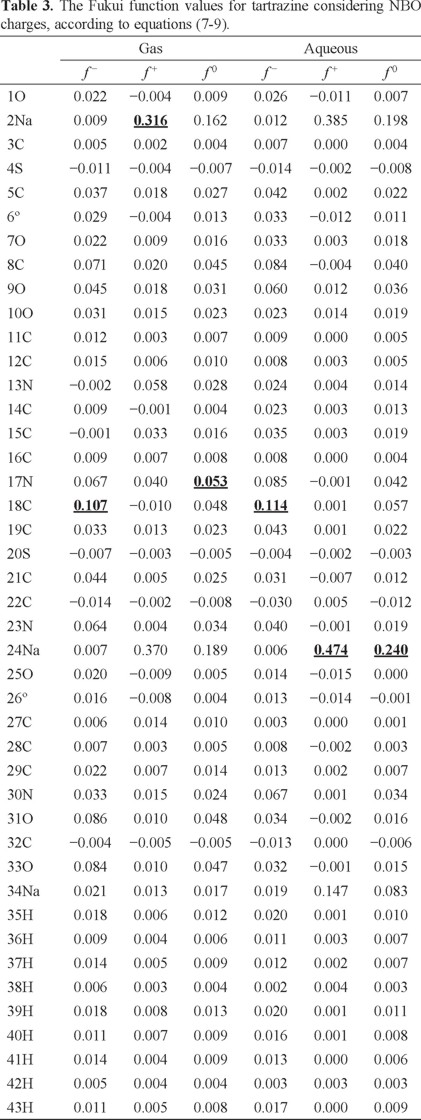
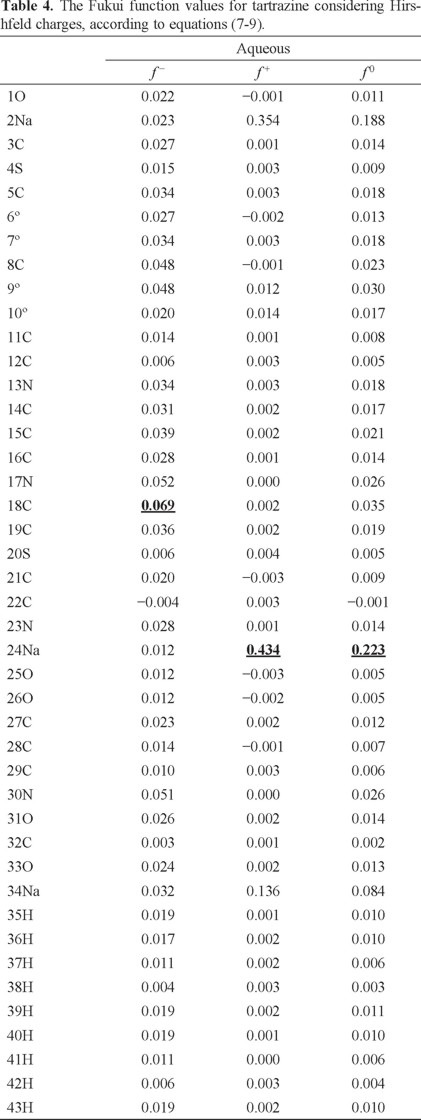
In order to evaluate the reactivity at atomic resolution, the Fukui Function was evaluated through equations (7-9). It is well known that the Fukui function allows determining the pin point distribution of the active sites on a molecule. However, the value of this function is completely dependent on the scheme of charges used. A variety of schemes to evaluate atomic charges has been reported. Most of them are based on some kind of population analysis. The arbitrariness in the way of choosing the charges has been one of the principal criticisms of the condensed Fukui function approximation [44]. Recently NBO charges have found good acceptation to calculate the condensed Fukui function and good agreement with the experimental results has been obtained comparable to those results obtained from electrostatic potentials and Hirshfeld charges [45-48]. Table 3 reports the values of the Fukui Function in terms of NBO charges. In the gas phase, the more reactive sites for an electrophilic, nucleophilic and free radical attacks were 18C, 2Na and 17N respectively. In the aqueous phase, the more reactive sites for an electrophilic, nucleophilic and free radical attacks were 18C, 24Na and 24Na respectively. In order to compare the reliability of the values of the Fukui function evaluated through NBO charges, the Fukui Function values were evaluated employing Hirshfeld charges. Table 4 reports the values of the Fukui Function for tartrazine in the aqueous phase employing Hirshfeld charges. The more reactive sites were 18C, 24Na and 24Na for an electrophilic, nucleophilic and free radical attacks, respectively. Note that the values of the Fukui Function obtained from NBO charges were totally coincident with the results obtained through Hirshfeld charges. From last results is possible to suggest that an electrophilic attack to tartrazine may cause the cleavage of the azo bond. However, a first attack on tartrazine by a nucleophile only would cause a nucleophilic substitution of Na atoms.
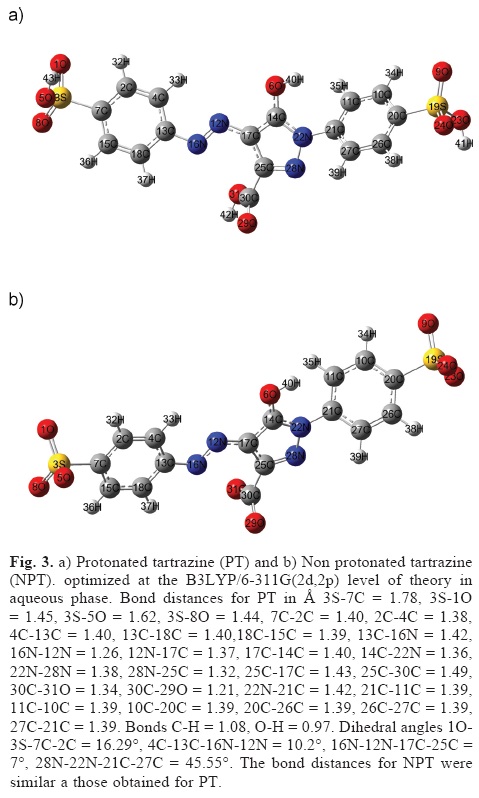
If we consider that the nucleophilic substitution on tartrazine is carried out in an aqueous system and at acid pH values. It is possible to suggest that the Na atoms are substituted by Hydrogens to form 3-carboxy-5-hydroxy-1-p-sulfophenyl-4-p-sulfophenylazopyrazole (protonated tartrazine), see Figure 3a. Note that a similar conclusion may be inferred, if tartrazine is attacked by a free radical. The global reactivity parameters for PT were I = 8.28 eV, A =1.86 eV, η = 6.42 eV, S = 0.16 eV, µ = -3.21 eV and ω = 0.80 eV. Note that PT is more stable and lesser electronegative than tartrazine because η and µ values are increasing. Also, PT is a better electrophile in comparison to tartrazine because its ω value is major in comparison to tartrazine.
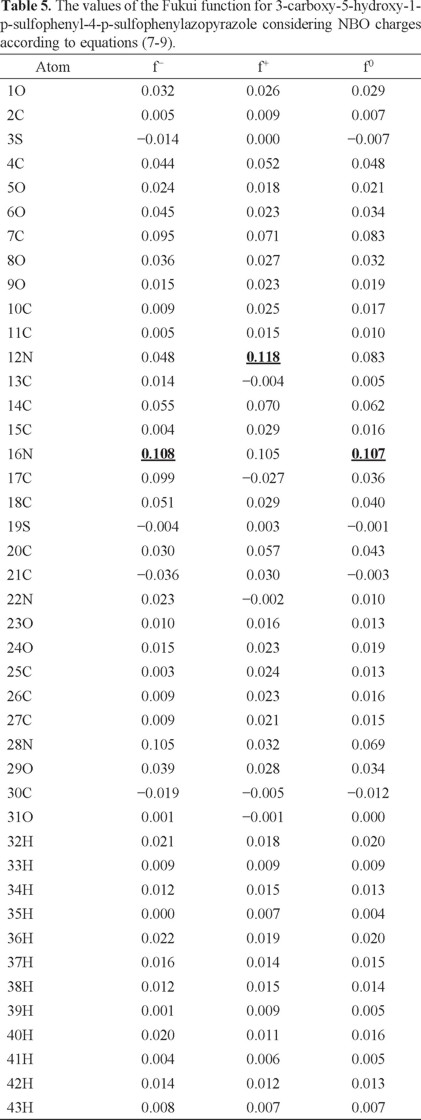
In order to analyze the local reactivity on PT, its Fukui Function values were calculated through equations (7-9), see Table 5. Note that the 16N atom is the most reactive site for both, electrophilic and free radical attacks. The most reactive site for a nucleophilic attack is located on the atom 12N. Last result suggests that the azo bond on PT is the most reactive zone of the molecule. Note that the azo bond is the most labile portion of an azo colourant according to available experimental reports which are coincident with the results obtained in the present work [49-58].
At basic pH, it is possible that tartrazine is non protonated (NPT) and its trianionic form is predominant, see Figure 3b. For NPT the global reactivity parameters calculated were I = 5.92 eV, A = 2.52 eV, η = 3.40 eV, S = 0.29 eV, µ = -1.70 eV and ω = 0.43 eV. Note that NPT is less stable and a better nucleophile than PT because its η and ω values diminish. According to the Fukuis function values (not shown), for NPT the more reactive sites were located on 16N, 12N and 16N for electrophilic, nucleophilic and free radical attacks respectively.
Figure 4 depicts a summary of our results through the schematization of possible pathways of the different attacks. If tartrazine is subject to an electrophilic attack, then a cleavage of the azo bond is expected, Figure 4a. A nucleophile attack on tartrazine would cause the substitution of Na atoms to produce either PT or NPT, depending of the pH value of the solution. A subsequent electrophilic or free radical attack will be necessary to cause the cleavage of the azo bond, see Figure 4b. Finally, if tartrazine is initially attacked by a free radical then, a subsequent attack by a nucleophile will be necessary to cleave the azo bond. It is important to mention that the proposed mechanisms are in agreement with the degradation products obtained by advanced catalytic oxidation [59] and electrochemical reduction processes [60]. Theoretical analyses of the better electrophiles, nucleophiles and free radicals to cleave the N=N bond are beyond of the scope of this paper; however they will be studied in future works.
Conclusions
In the present work DFT reactivity descriptors for tartrazine were calculated employing DFT theory in the gas and aqueous phases. The results suggested that the solvation modifies the values of the chemical reactivity descriptors. It was possible to observe that an electrophilic attack directly cleaves the azo bond, while nucleophilic or free radical attacks require additional attacks to cleave the same bond.
Methodology
A starting geometry was generated using the PM6 method [61] implemented in Mopac 2012 [62]. The optimal conformation was subjected to full geometry optimization in gas phase employing the hybrid functional B3LYP [63-65] and the basis set 6-311++G(2d,2p) [66, 67]. The optimized tartrazine in the gas phase was optimized at the B3LYP/6-311++G (2d,2p) level employing the PCM solvation model [68, 69]. The vibrational frequencies for all cases were computed to make sure that the stationary points were minima.
Computational resources
All the calculations reported here were performed with the package Gaussian 09 [70] and visualized with the GaussView V. 3.09 [71] packages.
Acknowledgments
L.H.M.H. gratefully acknowledges the financial support of the Universidad Autónoma del Estado de Hidalgo.
References
1. Alagirusamy, R.; Das, A. Technical Textile Yarns, 1st Edition, Woodhead Publishing, 2010. [ Links ]
2. Amin, K. A.; Hameid, H. A.; Elsttar, A. H. A. Food Chem. Toxicol. 2010, 48, 2994-2999. [ Links ]
3. Miller, K. Intolerance to food colours and other additives. In: K. Miller and S. Nicklin (Eds.), Immunology of the Gastrointestinal Tract, CRC Press Inc., Boca Raton, FL, 1987, 85594. [ Links ]
4. Lackey, S. D. Ann. Allergy 1977, 38, 206-214. [ Links ]
5. Özdemir, Y.; Akkan, A. A. Turk. J. Chem. 1999, 23, 221-229 [ Links ]
6. Wang, J.; Chen, G.; Zhu, T.; Gao, S.; Wei, B.; Bi, L. Chin. Opt. Lett. 2009, 7, 1058-1060. [ Links ]
7. Reddy, M. S.; Ahmed, M. S. M.; Aswini, C. Res. Rev. RRJET, 2013, 2(3), 218-228. [ Links ]
8. Mittal, A.; Kurup, L.; Mittal, J. J. Hazard. Mater. 2007, 146, 243-248). [ Links ]
9. Lackey, S. D. Ann. Allergy 1959, 17, 719-721. [ Links ]
10. Thuvander, A. 1995, 92(4), 296-298. [ Links ]
11. MacCara, M. E. Can. Med. Assoc. J. 1982, 126(8), 910-914. [ Links ]
12. Lockey, S. D. Ann. Allergy, 1977, 38(3), 206-210. [ Links ]
13. Stevenson, D. D.; Simon, R.A.; Lumry, W.R.; Mathison, D.A. J. Allergy Clin. Immunol. 1986 , 78, 182-191. [ Links ]
14. Borzelleca, J. F.; Hallagan, J.B. Food Chem. Toxicol. 1988, 26(3), 179-187. [ Links ]
15. Sushmita, B.; Chattopadhyaya, M.C. Arab. J. of Chem. 2013, In Press. [ Links ]
16. Ruiz, A. A. Producción + Limpia 2011, 6(2), 58-77. [ Links ]
17. Modirshahla N.; Behnajady M.S.; Kooshaiian, S. Dyes Pigm. 2007, 74, 249-257. [ Links ]
18. Gupta, V. K.; Jain, R.; Nayak, A.; Agarwal, S.; Shrivastava, M. Mater. Sci. Eng. C 2011, 31, 1062-1067. [ Links ]
19. Al-Dawery, S. K. J. Eng. Sci. Tech. 2013, 8(6), 683-691. [ Links ]
20. Salem, M. A.; Gemeay, A. H. Monatshefte für Chemie 2000, 131(2), 117-129. [ Links ]
21. Ghalwa, N. A.; Abu-Shawish, H. M.; Tamous, H. M.; Harazeen, H. A. Chemistry Journal 2013, 3(1), 1-6. [ Links ]
22. López-de-Alba, P. L.; López-Martinez, L.; Michelini-Rodriguez, L. I.; Wrobel, K.; Wrobel, K.; Amador-Hernández, J. Analyst 1997, 122, 1575-1579. [ Links ]
23. Sudha, M.; Saranya, A.; Selvakumar, G.; Sivakumar, N. Int. J. Curr. Microbiol. App. Sci. 2014, 3(2), 670-690. [ Links ]
24. Patel, R.; Suresh, S. J. Hazard. Mat. 2006, 137, 1729-1741. [ Links ]
25. Mendoza-Huizar, L.H.; Rios-Reyes, C.H. J. Mex. Chem. Soc. 2011, 55(3), 142-147. [ Links ]
26. Peica, N.; Pavel, I.; Pînzaru, S. C.; Rastogi, V. K.; Kiefer, W. J. Raman Spectrosc. 2005; 36, 657-666 [ Links ]
27. Shahir, A. A.; Javadian, S.; Razavizadeh, B. B. M.; Gharibi, H. J. Phys. Chem. B 2011; 115(49), 14435-14444. [ Links ]
28. Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules, Oxford University Press , New York, 1989. [ Links ]
29. Gázquez, J. L. J. Mex. Chem. Soc. 2008, 52(1), 3-10. [ Links ]
30. Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103, 1793-1874. [ Links ]
31. Parr, R. G.; Donnelly, R. A.; Levy, M.; Palke, W. E. J. Chem. Phys. 1978, 68, 3801-3807. [ Links ]
32. Parr, R. G.; Pearson, R. G. J. Am. Chem. Soc. 1983, 105, 7512-7516. [ Links ]
33. Pearson, R. G. J.Chem. Ed. 1987, 64, 561-562. [ Links ]
34. Parr, R.G.; Szentpaly, L.; Liu, S. J. Am. Chem. Soc. 1999, 121, 1922-1924. [ Links ]
35. Ayers, P.W.; Parr, R.G.; Pearson, R.G. J. Chem. Phys. 2006, 124, 194107-194121. [ Links ]
36. Ayers, P.W. Faraday Discuss. 2007, 135, 161-190. [ Links ]
37. Liu, S.B. in Chemical reactivity theory: A density functional view, edited by P.K. Chattaraj, Taylor and Francis, Boca Raton, 2009. [ Links ]
38. Parr, R.G.; Yang, W. J. Am. Chem. Soc. 1984, 106, 4048-4049. [ Links ]
39. Ayers, P. W.; Parr, R. G. J. Am. Chem. Soc. 2000, 122, 2010-2018. [ Links ]
40. Chattaraj, P. K.; Lee, H.; Parr, R.G. J. Am. Chem. Soc. 1991, 113, 1855-1856. [ Links ]
41. Ayers, P.W. J. Chem. Phys. 2005, 122, 141102-141104. [ Links ]
42. Gazquez, J. L.; Mendez, F. J. Phys. Chem. 1994, 98, 4591-4593. [ Links ]
43. Mendez, F., Gazquez, J. L. J. Am. Chem. Soc. 1994, 116, 9298-9301. [ Links ]
44. Fuentealba, P.; Florez, E.; Tiznado, W. J. Chem. Theory Comput. 2010, 6, 1470-1478. [ Links ]
45. Nazari, F.; Zali, F.R. J. Mol. Struct. (Theochem) 2007, 817, 11-18. [ Links ]
46. Daoud, I.; Mesmoudi, M.; Ghalem, S. Int. J. Chem. Anal. Sci. 2013, 4, 49-56. [ Links ]
47. López, J.M.; Ensuncho, A.; Robles, J. Inf. Tecnol. 2013, 24(3), 3. [ Links ]
48. Mendoza Huizar, L. H.; Rios-Reyes, C. H.; Olvera-Maturano, N. J.; Robles, J.; Rodriguez, J. A. Open Chem. 2015, 13, 52-60. [ Links ]
49. Weber E. J.; Adams R. L. Environ Sci Technol. 1995, 29(5), 1163-1170. [ Links ]
50. Shu, H. Y.; Huang C.R.; Chang, M.C. Chemosphere 1994, 29(12), 2597-2607. [ Links ]
51. Bartsch H. IARC Sci. Publ. 1981, 40,13-30. [ Links ]
52. Chung, K. T. Mutat. Res. 1983, 114, 269-281. [ Links ]
53. Chung, K. T. J Environ. Sci. Health C 2000, 18, 51-74. [ Links ]
54. Levine, W. G. Drug Metab. Rev. 1991, 23, 253-309. [ Links ]
55. Chung KT, Cerniglia CE. Mutat Res. 1992, 277, 201-220 [ Links ]
56. Xu, H.; Heinze, T. M.; Paine, D. D.; Cerniglia, C. E.; Chen, H. Anaerobe 2010, 16, 114-119. [ Links ]
57. Sperry, K. Am. J. Forensic Med. Pathol. 1992, 13(1), 7-17. [ Links ]
58. Engel, E.; Vasold, R.; Santarelli, F.; Maisch, T.; Gopee, N.V.; Howard, P.C.; Landthaler, M.; Baumler, W. Exp. Dermatol. 2010, 19, 54-60. [ Links ]
59. Beach, E. S.; Malecky, R. T.; Gil, R. R.; Horwitz, C. P.; Collins, T. J. Catal. Sci. Technol. 2011, 1, 437-443. [ Links ]
60. Jain, R.; Bhargava, M.; Sharma,. N. Ind. Eng. Chem. Res. 2003, 42, 243-247. [ Links ]
61. Stewart, J. J. P. J. Mol. Mod. 2007, 13, 1173-1213. [ Links ]
62. Mopac 2012, Stewart JJP (2012) MOPAC2012 Version 8.032 L. Stewart Computational Chemistry, Colorado Springs. [ Links ]
63. Becke, A. D. J. Chem. Phys. 1993, 98, 5648-5652. [ Links ]
64. Becke, A. D. Phys. Rev. A 1988, 38, 3098-3100. [ Links ]
65. Lee, C.; Yang, W.; Parr, R.G. Phys. Rev. B 1988, 37, 785-789. [ Links ]
66. Krishnan, R.; Binkley, J. S.; Seeger, R.; Pople, J. A. J. Chem. Phys. 1980, 72, 650-654. [ Links ]
67. McLean, A. D.; Chandler, G. S. J. Chem. Phys. 1980, 72, 5639-5648. [ Links ]
68. Miertus, S.; Tomasi, J. J. Chem. Phys. 1982, 65, 239-45. [ Links ]
69. Miertus, S.; Scrocco, E; Tomasi J. J. Chem. Phys. 1981, 55, 117-129. [ Links ]
70. Gaussian 09, Revision A.01, Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Mont-gomery, J. A., Jr.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, N. J.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, Ö.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. Gaussian, Inc., Wallingford CT, 2009. [ Links ]
71. Gaussview Rev. 3.09, Windows version. Gaussian Inc., Pittsburgh.














