Article

 

A Comparison of the Accuracy of Semi-empirical PM3, PDDG and PM6 methods in Predicting Heats of Formation for Organic Compounds

 

Yang-Yang Wu¹, Feng-Qi Zhao², and Xue-Hai Ju¹*

 

¹ Key Laboratory of Soft Chemistry and Functional Materials of MOE, School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing 210094, P. R. China. xhju@njust.edu.cn

² Laboratory of Science and Technology on Combustion and Explosion, Xi'an Modern Chemistry Research Institute, Xi'an 710065, P. R. China.

 

Received February 12^th, 2014
Accepted April 7^th, 2014

 

Abstract

Gas phase heats of formation (HOF) of 18 kinds of 390 organic compounds were calculated by quantum chemical calculation using semi-empirical PM3, PDDG and PM6 methods. The calculated HOFs were compared with the experimental data to illustrate the accuracy for different kinds of organics. Furthermore, the calculated values were linearly fitted with experimental values using the least square method, and were afterward substituted into the fitted regression equations to obtain the calibrated ones. The results show that, for 10 kinds of the selected organics, PM6 is more accurate, and PDDG is more accurate for 7 kinds of organics, while PM3 is only good for amino acid. As a whole, PM6 predicts the HOFs more accurately, with its weighted total mean average deviation (WTMAD) being 0.4 kJ/mol and 2.4 kJ/mol smaller than those of PM3 and PDDG, respectively. On the other hand, our results show that PDDG is the best to differentiate the isomers, with its mean average deviation (MAD) for isomerization energy being 7.8 kJ/mol and 11.0 kJ/mol smaller than PM6 and PM3, respectively. After the calibration, the values of MADs from the PM3, PDDG and PM6 results for most organics are reduced by 0.1 to 18.2 kJ/mol, with exceptions of the PM3 for amines, PDDG for carboxylic acids, and PM6 for ethers.

Key words: Heat of formation (HOF); semiempirical molecular orbital theory; PM3; PDDG; PM6; linear fitting.

 

Resumen

Se calcularon los calores de formación en fase gaseosa (HOF) de 390 compuestos orgánicos agrupados en 18 familias de compuestos con química cuántica, utilizando los métodos semiempíricos PM3, PDDG y PM6. Los valores calculados de HOFs fueron comparados con los valores experimentales correspondientes, con el fin de evaluar la precisión de los métodos para describir cada una de las diferentes familias de compuestos. Para esto, los valores calculados y experimentales de HOF fueron ajustados a una línea recta por el método de mínimos cuadrados, las ecuaciones de ajuste fueron utilizadas como curvas de calibración. Estas curvas muestran que para 10 familias de compuestos, el método PM6 es el mejor; mientras que el PDDG es mejor para 7 familias de compuestos orgánicos y, el PM3 es bueno sólo para los aminoácidos. De manera general, el método PM6 predice con mejor aproximación los valores de HOF con un desviación media promedio (WTMAD) de 0.4 kJ/mol, un valor 2.4 kJ/mol menor que el que presentan los métodos PM3 y PDDG. Por otra parte, se muestra que el PDDG es el mejor método para diferenciar los isómeros, con un desviación media promedio (MAD) más pequeña para la energía de isomerización en 7.8 kJ/mol y 11.0 kJ/mol, con respecto a PM3 and PDDG, respectivamente. A través de la calibración, los valores de MADs obtenidos para PM3, PDDG y PM6 para la mayoría de los compuestos estudiados disminuyeron de 0.1 a 18.2 kJ/mol, con excepción para el PM3 de las aminas, PDDG para los ácidos carboxílicos y el PM6 para los éteres.

Palabras clave: Calor de formación (HOF); teoría semiempírica de orbitales moleculares; PM3; PDDG; PM6; regresión lineal.

 

Introduction

Quantum chemical computations can direct researchers to design and tailor target molecules while reducing the costs associated with experiments, and it is especially useful to screen the high energy materials (HEM) [1] since the experimental conditions of HEM are quite rigorous. As one part of the computational chemistry, semi-empirical methods have played a significant role during the second half of the 20th century. Although the first-principles quantum chemical methods are overwhelmingly used nowadays due to their high accuracy as a whole, the semi-empirical methods still have some advantages. They employ a minimum valance basis set, parameters and integral approximations such as NDDO (Neglect of Diatomic Differential Overlap) [2]. Consequently, the semi-empirical methods are fast, making them widely used in the application for large molecules as reviewed in many reports [3-6]. In particular, they produce the heats of formation (HOFs) directly. The HOF is a quite important and useful thermodynamic parameter, which is always used to describe the stability of compounds. Also, it can be used to calculate the heats of reactions and changes of free energy to decide whether or not a reaction occurs spontaneously. In particular, the HOF is very useful in calculating thermodynamic properties of HEM, whose performances, such as detonation velocity and explosion heat, are closely related to the HOF [7]. Moreover, though the first principle methods should be more accurate than semi-empirical methods as a whole, it is reported that semiempirical methods predict the HOF even more accurately than some DFT methods [8]. As reviewed in many reports, the semi-empirical method includes CNDO/1, CNDO/2, MINDO/3 [9], AM1 [10], PM3 [11], PDDG/PM3 [12] and PM6 [13] etc. AM1 has included some hydrogen-bonded structures and energies in the parameterization, and the PM3 was further modified than AM1 by means of optimizing parameters. Thus PM3 is more accurate for HOFs and the hydrogen-bond geometries than AM1 [14]. Later on, based on the PM3 semi-empirical method, Repasky et al. introduced a single function, that is the Pairwise Distance Directed Gaussian (PDDG) function, to enhance the NDDO-based semiempirical method. This results a reduction in mean absolute error from 4.4 kcal/mol by PM3 to 3.3 kcal/mol by PDDG for the HOFs of 622 diverse molecules containing C, H, N, and O atoms. About five years later, the parameters in the PM6 were optimized further by Stewart et al, with specific emphasis on the biochemistry and transition metal systems also on the base of PM3. For a subset of 1373 compounds involving only the elements H, C, N, P, Cl, S, Br, O and F, PM6 yields a mean absolute error of 4.4 kcal/mol while PM3 yields 6.3 kcal/mol [12]. Though it is known now that PM6 and PDDG both perform better than PM3 in predicting the HOFs, no one has ever compared the precision between PM6 and PDDG. On the other hand, it is also very interesting to explore the comparison among the precision of PM3, PDDG and PM6 for different series of organic compounds, because the inner modification method in each semi-empirical method makes its accuracy different for different series of organic compounds. In this paper, we computed the HOFs of 18 series of 390 organic compounds to evaluate the accuracy of the PM3, PDDG and PM6 methods. Since the semi-empirical computational methods such as PM3, PDDG or PM6 have the inner systematic errors, we established the relationship between the computed results and the experimental values by the least square regression method.

 

Computational methods

All the computations were carried out using PM3, PDDG and PM6 methods as implemented within Gaussian 09 program [15]. The geometries of all compounds were fully optimized. The mean absolute deviations (MAD), mean signed deviations (MSD, calculated value minus experimental value), root mean square deviations (RMSD) and the weighted total MADs (WTMAD) were used for overall statistical analysis. The WTMAD is defined as below:

where n_i represents the number of each kind of organic compound. The relationship between the computed results and the experimental values was established by the least square method to obtain a fitted equation, which can be expressed as:

ΔH_{f, expt.} = a * ΔH_{f, calc.} + b     (2)

where ΔH_{f, expt.} and ΔH_{f, calc.} represent the experimental and the calculated HOFs [16], respectively. In return, this relationship was used to calibrate the calculated results with the systematic errors being checked.

 

Results and discussion

The HOFs by the PM3, PDDG and PM6 methods for 390 organic compounds belonging to 18 kinds have been calculated, and their respective MADs as well as those of their calibrated results with respect to the experimental values were listed in Table 1. As shown in Table 1, for 10 kinds of organic compounds in this paper, the MADs of the calculated results by PM6 are smaller than those by PM3 and PDDG, especially for aldehyde, for which the MADs from PM6 results are 14.6 kJ/mol and 9.4 kJ/mol smaller than (both nearly half of) those from PM3 and PDDG, respectively. On the contrary, PM6 yields larger MADs than PM3 and PDDG for alkane by 12.7 kJ/mol and 15.9 kJ/mol, respectively, for carboxylic acid by 9.0 kJ/mol and 11.1 kJ/mol, for amino acid by 3.8 kJ/mol and 2.3 kJ/mol, and for amine by 1.5 kJ/mol and 4.8 kJ/mol. On the other hand, PM3 produces the smallest MAD among these three methods only for amino acid, 1.5 kJ/mol and 4.8 kJ/mol smaller than PDDG and PM6, respectively. While for alkane, halogenated alkane, halogenated alkene, cycloalkene, carboxylic acid, amine and nitro compound, PDDG gives the smallest MAD among the three methods. However, for alkene, aromatic compounds, ketone and heterocyclic compounds, PDDG gives the largest MAD. MAD has been used widely to evaluate the accuracy of one method, such as in Ref. [11-13]. Thus from the viewpoint of MAD, PM6 is more accurate in predicting the HOF than PM3 and PDDG for 10 kinds of organic compounds, in which PM6 is obviously better than PM3 and PDDG for aldehyde. While PDDG is the best in reproducing the HOF for 7 kinds of organics, and PM3 is the most reliable only with respect to amino acid. Table 1 also lists the WTMADs of the three semi-empirical methods for the total 18 kinds of organics. We can see from Table 1 that the WTMADs of the three methods (namely PM3, PDDG and PM6), are 14.8 kJ/mol, 12.8 kJ/mol and 12.4 kJ/mol, respectively. This indicates that PM6 is more accurate than PM3 and PDDG in predicting the HOF for the selected 18 kinds of organics as a whole. It is worth noting that for the alkane, when the number of carbon atoms n ≤ 11, PM3 and PDDG are more reliable than PM6 as a whole. However, when n > 11, PM6 would be more accurate than PM3 and PDDG, while PDDG is slightly better than PM3. This may be due to the fact that the contribution of inner molecular interaction (such as core-core repulsion) in larger molecules would be more significant, and PM6 has done much modification on the core-core repulsion, while PDDG just only does a small modification on the base of PM3 [12,13]. Similar reasons can also explain that the absolute errors of the PM3 results reach 53.6 kJ/mol and 44.2 kJ/mol for 1,2-propanediol and 2,3-butanediol, respectively, since there are stronger intra-molecular repulsions, which PM3 fails to reproduce, between their two adjacent hydroxys in these two diols.

As for the case after the calibration using the fitted regression equations, we can also see in Table 1 that PM6 still yields the smallest MADs for 11 kinds of organics, and PDDG yields the smallest MADs for 5 kinds, leaving PM3 producing the smallest MAD for cycloalkene only. Calibrated PDDG produces the largest MADs for halogenated alkene (for which it produces the smallest MAD before the calibration) and aromatic compounds, while PM6 for amino acid only and PM3 for the rest 15 kinds. For the whole 18 kinds of organics, from the viewpoint of WTMAD, calibrated PM6 still gives the most accurate HOF with WTMAD of 8.0 kJ/mol, and PDDG is the second with WTMAD of 9.1 kJ/mol, PM3 being the last with WTMAD of 10.9 kJ/mol. Also, Table 1 lists the variation in MADs of PM3, PDDG and PM6 results after being calibrated by the fitted regression equations for each kind of organics. After the calibration by the fitted equations, for 15 kinds of the organics, the MADs of the calculated HOFs by all the three methods can be reduced more or less, which means that the calibration is effective to these organics. Moreover, calibrations on the calculated results for some organic compounds, such as alkane by PM6, cycloalkene, aldehyde and nitrile by PM3, aldehyde by PDDG, are quite effective. The values of MADs are reduced by 17.0, 13.0, 18.2, 13.2, and 14.1 for the above mentioned compounds, respectively. However, there are three exceptions. One is ether, for which the MAD of HOFs calculated by PM6 increases by 0.1 kJ/mol after the calibration. Another is amine, for which the MADs of HOFs by PM3 increases by 1.2 kJ/mol after calibrating, and the third one is carboxylic acid by PDDG with its MAD increased by 0.3 kJ/mol.

Table 2 lists the parameters of the fitted equations of each category for PM3, PDDG and PM6 methods, as well as the correlation coefficients and the standard deviations (SDs). Table 2 shows that the correlated coefficients of the fitted equations from the PDDG results are closer to 1.000 than those of PM3 and PM6, with three exceptions of ketone, nitrile and amine. For these three kinds of organics, the correlated coefficients of the fitted equations of PM6 are closer to 1.000. This suggests that PDDG is relatively more stable than PM3 and PM6. However, the SDs of the fitted equations of PM6 are smaller than those of PM3 and PDDG for 11 kinds of organics, and this demonstrates again that PM6 is more accurate than PM3 and PDDG as a whole.

As for why PDDG is more accurate than PM3 as a whole, it is mainly due to the novel addition of the Pairwise Distance Directed Gaussian (PDDG) function into the CRF (core repulsion function) [9]. As for the advantages of PM6 over PM3, the parameters in the PM6 has been specifically optimized for organic compounds containing only C, H, O, N, F, S, Cl, I, P and S based on PM3 [13]. In addition, PM6 used a larger training set for optimizing its parameters than PM3 [17]. The difference between the calculated HOFs by PM3 and PM6 for the same organic compounds is derived from two aspects: 1) modifications in the approximations; 2) optimizations of the atomic parameters. The parameters were determined by means of making the value of error function S smallest:

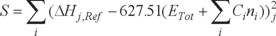
where the ΔH_j,Ref are the experimental HOFs of the compounds, the E_Tot are the calculated total energies, the C_i are constants for each atom of type i, and n_i are the number of atoms of that type. The error function S contains E_Tot which depends on the approximations in the calculation process, so the accuracy of parameters would be influenced by the adopted approximations. In addition, the number of reference data used in PM6 (about 9000 discrete species) is ten times more than that in PM3 (about 800 discrete species) [13]. The advancements in the optimizations of PDDG and PM6 enable their accuracy over PM3 for organic compounds as a whole, but it can not ensure that the two methods are more accurate than PM3 for each kind of organic compounds. Actually PDDG is worse than PM3 for alkene, aromatic compounds, ketone and heterocyclic compounds, and PM6 is worse than PM3 for alkane, carboxylic acid, amino acid and amine. On the other hand, though PM6 adopts a much larger reference data than PM3, the weight (individual number / total number) of each kind of organic compound in the reference data is different during the optimization of the parameters. This will more or less influence the final accuracy of the parameters of atoms, which is another reason why the accuracy of PM6 for different kinds of organic compounds is different. Moreover, it is worthy to note that the above results that PM3 is better than PM6 for amine, carboxylic acid and amino acid, indicating that PM6 is not better than PM3 when treating the groups of -COOH and -NH₂.

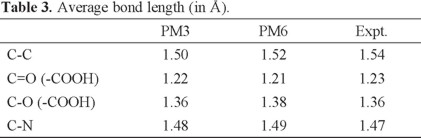
To further investigate why PM6 is not better than PM3 for alkane, carboxylic acid, amino acid and amine, we compared some bond lengths from the PM3 and PM6 methods. As can be seen in Table 3, the bond lengths of C-N and C-O (in -COOH) by PM6 are longer than experimental values, while the bond lengths by PM3 are shorter than experimental values. This can be explained by the fact that the modifications in PM6 make the core-core repulsion stronger. The bond length of C=O by PM6 is shorter than that by PM3, due to the variation of the corresponding atomic parameters. The bond lengths of C-N, C=O and C-O by PM3 are closer to the experimental values than PM6, which may explain partly why PM3 is better than PM6 for amine and carboxylic acid. Nevertheless for C-C, the bond length by PM6 is more accurate than that of PM3, which is opposite to the fact that the HOF of alkane by PM3 is more precise than that by PM6. The number of reference data in PM6 is much larger than that in PM3 as mentioned above, and this in return causes weight of alkane in the reference data in PM3 larger than that in PM6, and finally enables PM3 more accuracy for alkane after the optimization of the atomic parameters.

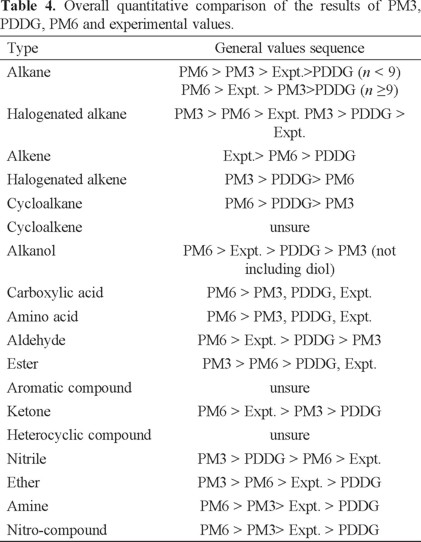
The selected 18 kinds of organic compounds are just parts of all the organic compounds, so we can not exclude the possibility that PM3 would be more accurate than PDDG and PM6 for some additional kind of organic compounds. We found that the quantitative sequence of the results computed by PM3, PM6 and the reported values varies for different kinds of organic compounds, as shown in Table 4. The results are all from the chain molecules to avoid the influence of the configuration of branch on the HOF, so that the contribution of functional groups is only taken into consideration.

The absolute error distributions of PM3, PDDG and PM6 results were depicted in bar diagrams (Fig. 1.), from which we can see that most of the absolute errors of the calibrated PM6 are less than 10 kJ/mol, which shows that the accuracy for HOF increases in the order of PM3 < PDDG < PM6 < calibrated PM3 < calibrated PDDG < calibrated PM6 as a whole.

In addition, it is reported that PDDG has a 43% improvement in calculating the isomerization energy than PM3 [12], then how about PM6 in differentiating isomers compared to the above two semi-empirical methods? Herein, we have also listed a number of isomerization energies by the three methods for a comparison in Table 5. As is shown in Table 5, before the calibration, from the viewpoint of MAD, PDDG can predict the isomerization energy best with the smallest MAD of 3.1 kJ/ mol, followed by PM6 with MAD of 10.9 kJ/mol, and PM3 is the worst. After the calibration, the MAD of PM6 is 0.2 kJ/mol less than that of PDDG, indicating that calibrated PM6 is slightly better in calculating the isomerization energy than calibrated PDDG, while calibrated PM3 still yields the largest MAD.

 

Conclusion

Our target of this paper is to evaluate the accuracy of HOFs from the PM6, PDDG as well as PM3 methods for different classes of organic compounds. The HOFs predicted by PM3 (maximum MAD is 25.4 kJ/mol, WTMAD is 14.8 kJ/mol), PDDG (maximum MAD is 20.6 kJ/mol, WTMAD is 12.8 kJ/mol) and PM6 (maximum MAD is 21.9 kJ/mol, WTMAD is 12.4 kJ/mol) are generally in good agreements with the reported experimental values, with PM6 being slightly better than PM3 and PDDG as a whole. The results also show that the linear relationship of PDDG results versus the experiment results is better than those of PM3 and PM6, which indicates that PDDG is more stable than PM3 and PM6 in predicting HOFs. At the same time, the use of fitted equation to calibrate the calculated results can more or less reduce the deviation as a whole, except for the HOF of amine by PM3, the HOF of carboxylic acid by PDDG and the HOF of ether by PM6. Moreover, PDDG performs the best in differentiating the isomers as a whole. Finally, our work shows that semi-empirical method of PM6 is an alternative choice for predicting the HOF, especially when the accuracy of HOF is not a great concern.

 

Acknowledgement

We gratefully acknowledge the funding provided by the Laboratory of Science and Technology on Combustion and Explosion (Grant No. 9140C3501021101) and the project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions for supporting this work.

 

Reference

1. Sikder, A. K.; Maddala, G.; Agrawal, J. P.; Singh, H. J. Hazard. Mater. A 2001, 84, 1-24.         [ Links ]

2. Pople, J. A.; Beveridge, D.L. Approximate Molecular Orbital Theory, McGraw-Hill, New York, 1970.         [ Links ]

3. Ellison, F. O. J. Phys. Chem. 1962, 66, 2294-2299.         [ Links ]

4. Jalali-Heravi, M.; McManus, S. P.; Zutaut, S. E.; McDonald, J. K. Chem. Mater. 1991, 3, 1024-1030.         [ Links ]

5. Feng, F.; Wang, H. Yu, J. G. J. Theor. Comput. Chem. 2009, 8, 691-712.         [ Links ]

6. Polaczek, J.; Szafrański, A. M.; Kazimirski, J. K.; Lisicki. Z. J. Chem. Thermodyn. 2001, 33, 565-579.         [ Links ]

7. Dorofeeva, O. V. J. Chem. Thermodyn. 2013, 58, 221-225.         [ Links ]

8. Stewart, J. J. P. J. Mol. Model. 2004, 10, 6-12.         [ Links ]

9. Bingham, R. C.; Dewar, M. J. S.; Lo, D. H. J. Am. Chem. Soc. 1975, 97, 1285-1293.         [ Links ]

10. Dewar, M. J. S.; Zoebisch, E. G.; Healy, E. F.; Stewart, J. J. P. J. Am. Chem. Soc. 1985, 107, 3902-3909.         [ Links ]

11. Stewart, J. J. P. J. Comput. Chem. 1989, 10, 209-220        [ Links ]

12. Repasky, M. P.; Chandrasekhar J.; Jorgensen W. L. J. Comput. Chem. 2002, 23, 1601-1622.         [ Links ]

13. Stewart, J. J. P. J. Mol. Model. 2007, 13, 1173-1213.         [ Links ]

14. Schröder, S.; Daggett, V.; Kollman, P. J. Am. Chem. Soc. 1991, 113, 8922-8925.         [ Links ]

15. Frisch M. J.; Trucks, G. W.; Schlegel, H. B. et al. GAUSSIAN 09; Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.         [ Links ]

16. D. R. Lide, CRC Handbook of Chemistry and Physics, 88th Edition, CRC Press, Taylor and Francis, Boca Raton, 2008.         [ Links ]

17. Stewart, J. J. P. J. Mol. Model. 2008, 14, 499-535.         [ Links ]