Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Journal of the Mexican Chemical Society
Print version ISSN 1870-249X
J. Mex. Chem. Soc vol.58 n.1 Ciudad de México Jan./Mar. 2014
Article
Kinetic Modeling of the Alkaline Decomposition and Cyanidation of Argentian Plumbojarosite
Francisco Patiño,1* Mizraim Uriel Flores,1 Iván Alejandro Reyes,1 Hernán Islas,1 Martín Reyes,1 and Guillermo Juárez2
1 Área Académica de Ciencias de la Tierra y Materiales, Universidad Autónoma del Estado de Hidalgo, Carretera Pachuca-Tulancingo km. 4.5, C.P. 42184, Mineral de la Reforma, Hidalgo, México. franpac@terra.com.mx
2 Centro de Investigaciones en Nuevos Materiales, Universidad Tecnológica de la Mixteca, Carretera a Acatlima, km 2.5, C.P. 69000, Huajuapan de León, Oaxaca, México.
Received April 16, 2013.
Accepted July 23, 2013.
Abstract
The used sample was a solid plumbojarosite-argentian jarosite-hydronium jarosite solution. The stoichiometry of the alkaline decomposition and cyanide reaction in alkaline medium were studied. Alkaline decomposition shows an induction period, as well as a conversion period. Results on the reaction order and activation energy are consistent with the spherical particle model with decreasing core and chemical control. Six partial models and three global models were developed in order to describe its basic behavior. In every case the models were validated and tested for a plumbojarosite conversion of X = 0.75
Key words: Plumbojarosite, stoichiometry, decomposition, alkaline, kinetics, models.
Resumen
La muestra utilizada es una solución sólida de plumboja-rosita-arjentojarosita-hidroniojarosita. Se estudió la estequiometría de la reacción de descomposición y la de cianuración en medio alcalino. La descomposición alcalina muestra un periodo de inducción y un periodo de conversión. Los resultados de orden de reacción y energía de activación son consistentes con el modelo de núcleo decreciente y control químico. Se desarrollaron seis modelos parciales y tres modelos globales para describir su comportamiento básico. En todos los casos los modelos fueron validados y probados para una conversión de plumbojarosita de X = 0.75.
Palabras clave: Plumbojarosita, estequiometría, descomposición, alcalina, cinética, modelos.
Introduction
All the known members of the jarosite family are represented by the general formula: M Fe3(SO4)2(OH)6, where M+ is H3O+, Na+, K+, Rb+, Ag+, NH4+, T1+, ½ Pb2+, ½ Hg2+ [1]. When one of these cations takes the place of M+, jarosite type compounds are formed. If the jarosite forms in nature, it receives a mineral name, while if it is obtained in the laboratory it receives a chemical name. When in nature ½ Pb2+ substitutes M+, the formed mineral is given the name plumbojarosite; when that substitution is done through a synthesis procedure, it receives the chemical name lead jarosite. Plumbojarosite is a mineral that forms in acid media rich in sulfates, including zones of sulfur-type ore deposits that have undergone erosion, as well as acid rock drainage or acid mine drainage, and it usually forms around galena [2]. Lead jarosite is formed in the leaching circuits of zinc, and in pressure oxidation leaching processes of lead sulfide concentrates with associated silver [3].
Studies on the characterization of lead jarosite synthesized at 97 oC have suggested that all of the products contain H3O+, Pb and Ag at different amounts according to the synthesis conditions. It is a solid ternary solution consisting of lead jarosite-hydronium jarosite-silver jarosite [3]. It is interesting to cite the lead jarosite structural model developed by Hendricks [4]: PbFe6 (SO4)4 (OH)12 with a = 7 Å and c = 34 A; where Pb2+ takes up only half of the sites that are normally taken by Ag+ cations. Therefore, part of the Pb2+ in the plumbojarosite can be replaced by 2 Ag+, but at some point the axis c = 34 Å breaks, resulting in axis c = 17 Å, which is typical of argentian jarosite.
The stability order of jarosites in function of iron precipitation degree is K > Ag > Rb > NH4 > Na> Pb [5, 6], while the stability order of jarosites in NaOH medium in function of their activation energy is Pb > Na > Rb> NH4 > K >Ag [7-12]. Jarosite residuals from the industry of lead and zinc usually contain silver, so through studies have been carried out on the alkaline cyanidation of these compounds [7-12]. It has also been found that these compounds incorporate arsenic in their lattice as AsO4 in a partial substitution of SO4, making jarosites appealing from an economic [3, 13] and environmental point of view [14, 15, 16]. Because of the importance of plumbojarosite as an effective silver collector, Dutrizac et al. [17, 18, 19] conducted through studies on the incorporation of silver in the lattice of jarosite type compounds, both in sulfate and chloride media, with the aim of preventing the loss of silver in those compounds during their precipitation in the hydrometallurgical circuits of zinc and lead.
Patiño et al. [20, 21] studied the kinetics of the alkaline decomposition and cyanidation of argentian plumbojarosite with the aim of establishing the stoichiometry of the reactions and the dependences on concentration of Ca(OH)2, NaOH and NaCN, as well as on temperature and particle size. However, those studies did not establish the partial and total kinetic expressions for the induction and progressive conversion periods. For this reason, this paper presents a comprehensive study on the kinetic modeling of the decomposition and cyanidation in alkaline media of argentian lead jarosite, validating each of the kinetic expressions established in this study.
Results and discussion
Nature of the reaction
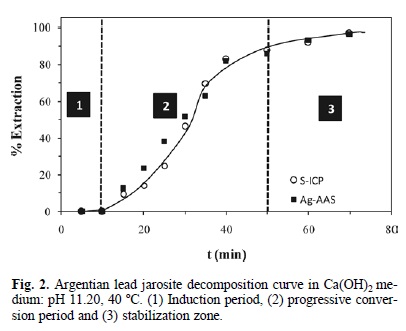
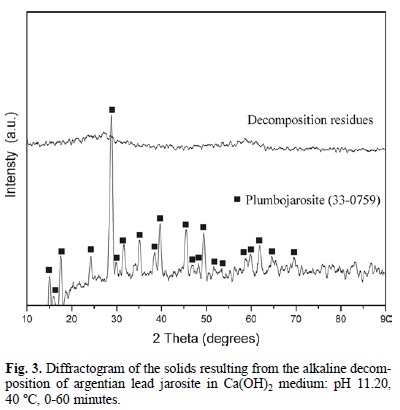
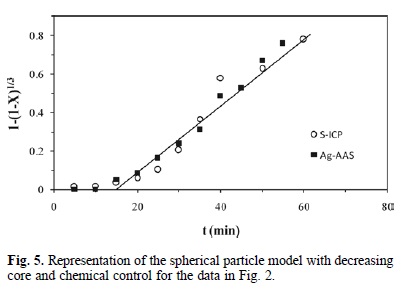
Fig. 2 shows that the alkaline decomposition and cyanidation of argentian lead jarosite presented an induction period (6), during which the yellow color of the jarosite showed no changes, and the concentration of sulfate and silver ions remained at trace levels in the solution. This generally indicates that the decomposition and cyanidation reaction have not started. The end of the induction period was recognizable for a change in the superficial color of the solid, which went from yellow to reddish. At the same time, the level of sulfate and silver ions in the solution increased progressively (Fig. 2) (as the reflection peaks of the argentian lead jarosite decreased until disappearing (Fig. 3). The stabilization of the concentration of sulfate and silver ions (Fig. 2) indicated that the decomposition and cyanidation reaction had finished. According to this, the alkaline decomposition process can be represented by:
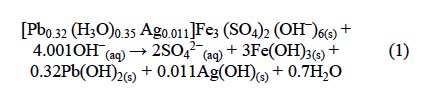

The solids resulting from the decomposition are made of a gel of amorphous iron, lead and silver hydroxides, as it occurs with the alkaline decomposition of other argentian jarosites, such as sodium jarosite, rubidium jarosite, potassium jarosite and ammonium jarosite [8, 9, 11, 23]. Silver in the decomposition gel was solubilized by the cyanide ion. Therefore, the alkaline decomposition and cyanidation of argentian lead jarosite can be described through two serial stages: first, a decomposition stage that controlled the overall process (Eq. 1), followed by a fast stage of complexation of Ag(OH)(s), as expressed by the following equation:
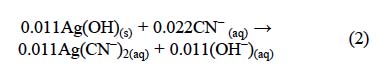
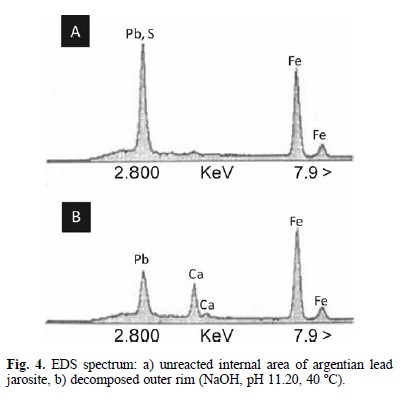
The SEM examination of polished thin sections of partially decomposed argentian lead jarosite proved to be difficult given the extremely small size of the jarosite crystals. However, EDS analysis (Fig. 4) is consistent with the formation of a reaction front. The spectrum of decomposed areas reveals the elimination of the sulfate ion, as well as the incorporation of the Calcium ion, which indicates that the decomposition products are porous enough to allow for the diffusion of ions in aqueous phase. Accordingly, the results of the alkaline decomposition and cyanidation of argentian lead jarosite are consistent with the spherical particle model with decreasing core and chemical control. This is confirmed in Fig. 5, where it can be noticed that the experimental data in Fig. 2 fairly match the mentioned model, which is expressed as [24, 25, 26]:
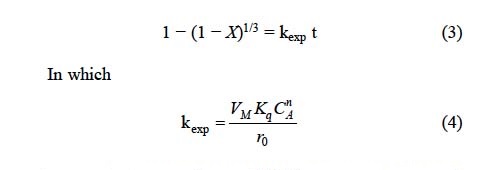
Where kexp = experimental rate constant; X = reacted mole fraction; VM = molar volume of the solid; Kq = chemical constant; CA = reactant concentration; r0 = initial radius and n = reaction order.
Modeling
Alkaline decomposition and cyanidation of argentian lead jarosite
Tables 1, 2 and 3 summarize the experimental results, in which the induction period (θ) and experimental rate constant (kexp) are present in a wide range of experimental conditions, such as NaOH, Ca(OH)2, NaCN, temperature and particle size. pH was constantly adjusted during the whole reaction, and the concentration of OH ions was calculated according to the ionization constant of water at the working temperature of each experiment, as previously mentioned in the experimental section [22].
Induction period
For the induction period of the decomposition of argentian lead jarosite in Ca(OH)2 medium with [OH-] > 3.39 x 10-4 mol L-1, a reaction order of n = 0.1 and an activation energy of Ea = 68.56 kJ mol-1 were obtained. In NaOH medium with [OH-] > 6.68 x 10-3 mol L-1, a reaction order of n = 1.19 and an activation energy of Ea = 66.38 kJ mol-1 were obtained. In the case of the cyanidation for [CN-] > 1.02 x 10-2 mol L-1, a reaction order of n = 0 and an activation energy of Ea = 167.78 kJ mol-1 were obtained. According to these results, the induction period for Ca(OH)2 is defined by the following expressions:
For [OH-] > 3.39 x 10-4 mol L-1
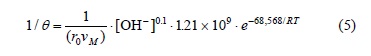
For the induction period in NA(OH) medium with [OH-] > 6.68 x 10-3, the following expression was obtained:
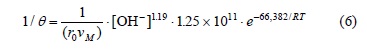
For the cyanidation with [CN-] > 1.02 x 10-2, the following expression was obtained:
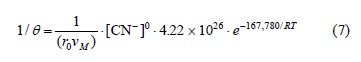
Progressive conversion period
Regarding the progressive conversion period of the argentian lead jarosite decomposition in Ca(OH)2 medium with [OH-] > 3.39 x10-4 mol L-1, a reaction order of n = 0.5 was obtained. The activation energy in Ca(OH)2 medium was of Ea = 45 kJ mol-1. Thus, the kinetic expression for the progressive conversion period in Ca(OH)2 medium is the following:
For [OH-] > 3.39 x 10-4 mol L-1
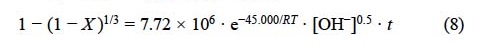
For the progressive conversion period corresponding to the decomposition of the argentian lead jarosite in NaOH media with [OH-] > 6.68 x10-3 mol L-1, a reaction order of n = 0.74 was obtained. The activation energy in NaOH was of Ea = 85.24 kJ mol-1. Therefore, the kinetic expression for the progressive conversion period in NaOH medium is:
For [OH-] > 6.68 x 10-3 mol L-1
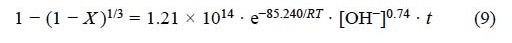
For the case of the argentian lead jarosite cyanidation with [CN-] > 1.02 x 10 2 mol L 1, a reaction order of n = 0 was obtained. The activation energy was Ea = 137.38 kJ mol-1. Thus, the kinetic expression for the cyanidation is the following:
For [CN-] > 1.02 x 10-2 mol L-1
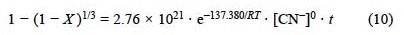
Fig. 6, 7 and 8 represent the model developed with equations 5, 6 and 7; they show the experimental induction period (θexp min) against the calculated induction period (θcalc min). Since the induction and progressive conversion periods have different magnitude orders, their values were plotted in a logarithmic fashion.
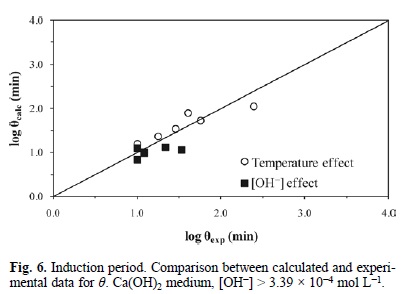
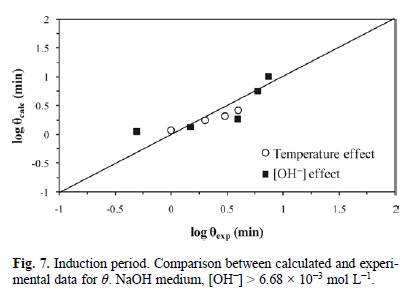
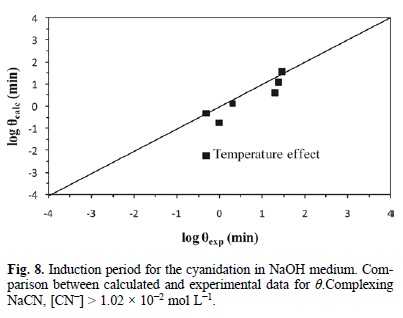
Fig. 9 represents the development of equation 8. It outlines the experimental rate constant against the calculated rate constant, i.e. kexp (min-1) Vs kcalc (min-1) in Ca(OH)2 medium. In the same way, Fig. 10 describes the development of equation 9, which represents the behavior of the progressive conversion period in NaOH medium. In the case of the cyanidation, Fig. 11 describes the development of equation 10, which corresponds to the behavior of the progressive conversion period in the cyanidation, with a constant concentration of OH ions.
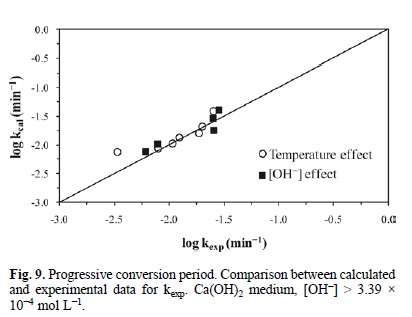
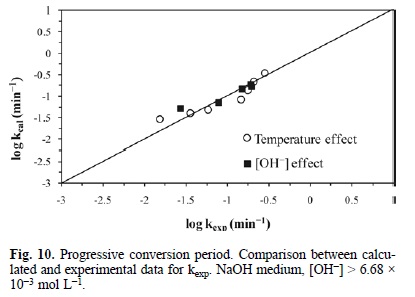
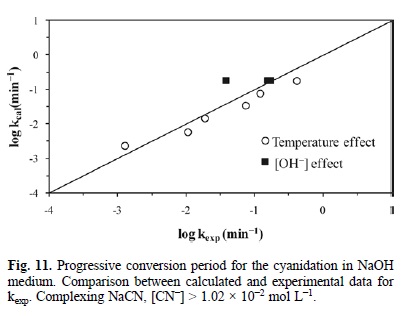
In all of the kinetic expressions VM = 169.02 cm3 mol-1, R = 8.3144 J mol-1 K, r0 in cm, T in Kelvin, [OH-] in mol L-1, [CN-] in mol L-1 and t in minutes.
From equations 5 and 8 corresponding to the alkaline decomposition in Ca(OH)2 medium with [OH-] > 3.39x10-4 mol L-1, a general expression can be established to determine the total reaction time necessary to obtain a complete conversion of the argentian lead jarosite. The kinetic model is the following:
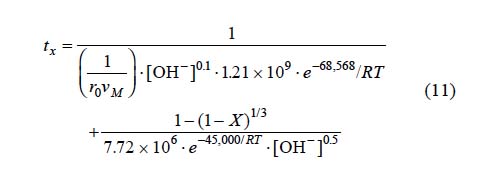
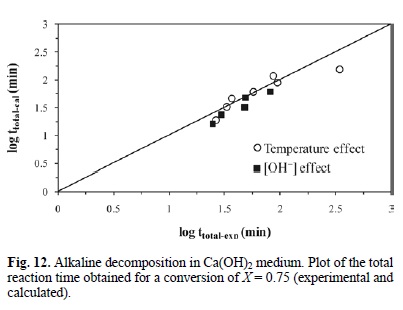
Fig. 12 shows the total reaction time necessary to obtain an argentian lead jarosite conversion of X = 0.75 (calculated according to equation 11) Vs the same parameter experimentally obtained. It can be concluded that equation 11 is consistent with the experimental results, because they do not differ considerably from the calculated data.
For equations 6 and 9 corresponding to the decomposition in NaOH with [OH-] > 3.39 x10-4 mol L-1, an expression was established to determine the total reaction time necessary to obtain a complete conversion of argentian lead jarosite. The kinetic model is the following:
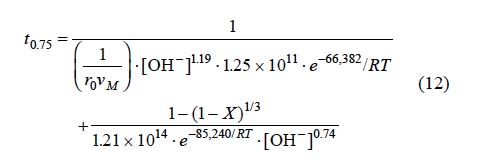
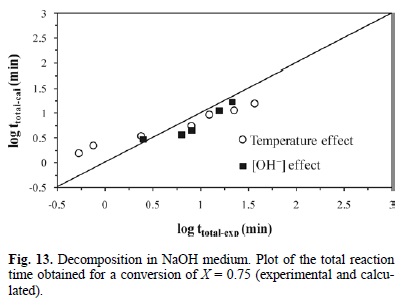
Fig. 13 shows the total reaction time necessary to obtain a conversion of X = 0.75 (calculated according to equation 12) Vs the same parameter (experimentally obtained). It can be concluded that equation 12 is consistent with the experimental results of the decomposition in NaOH medium.
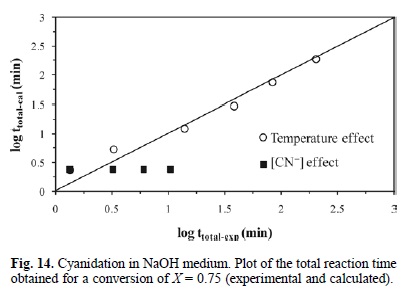
For equations 7 and 10 corresponding to the cyanidation in NaOH medium with [CN-] > 1.02 x10-2 mol L-1, an expression was established to determine the total reaction time necessary to obtain a complete conversion of argentian lead jarosite. The kinetic model is the following:
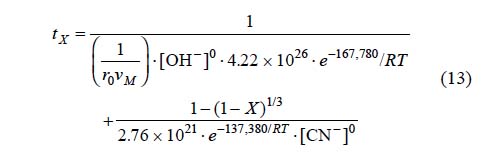
Fig. 14 shows the total reaction time necessary to obtain a silver dissolution of X = 0.75 (calculated according to expression 13) Vs the same parameter (experimentally obtained). According to the obtained data, we can conclude that expression 13 is consistent with the experimental results.
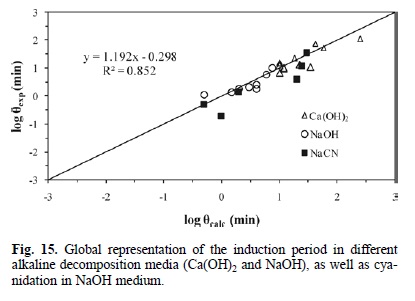
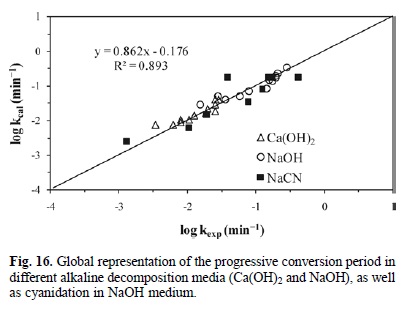
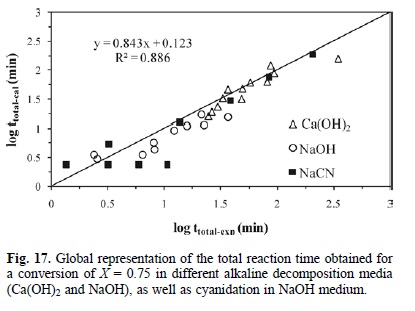
Fig. 15 outlines the calculated induction times Vs the experimental induction times in different media for alkaline decomposition (Ca(OH)2 and NaOH) and cyanidation in NaOH medium. It confirms that the experimental data are consistent with the kinetic models of equations 5, 6 and 1. Accordingly, Fig. 16 presents the calculated rate constants Vs the experimental rate constants for the progressive conversion period in different media for alkaline decomposition (Ca(OH)2 and NaOH) and cyanidation (NaCN), confirming that both experimental and calculated data are consistent with the kinetic models of Equations 8, 9 and 10. In a similar way, Fig. 17 shows the total reaction time necessary to obtain a conversion of X = 0.15 in different media for decomposition (Ca(OH)2 and NaOH) and cyanidation. It confirms that the experimental and calculated data are consistent with the global kinetic models of equations 11, 12 and 13.
Conclusions
The expressions of the global mathematical models for the alkaline decomposition of argentian lead jarosite regarding the induction period and progressive conversion period in Ca(OH)2 medium with [OH-] > 3.39x10-4 mol L-1 and in NaOH medium with [OH-] > 6.68 x 10-3 mol L-1, as well as for the cyanidation in NaOH medium with [CN-] > 1.02 x10-2 mol L-1, are the following:

Experimental
Materials
Argentian lead jarosite with a formula of (Pbo.32H3O35Ago.11) Fe3(SO4)2(OH)6 was used for this study. It was synthesized as described in previous works [3, 21]. The jarosite particles consist of rhombohedral crystal aggregates with a particle size of 7 pm and a density of 3170 kg m-3. Fig. 1 is an aggregate particle. Extensive characterization of argentian lead jarosite can be found in previous works by Patiño et al. [3].
Experimental procedure
The used experimental procedure was similar to that of previous works [6, 20]. For the decomposition in NaOH, 0.25 g of argentian lead jarosite were suspended in a volume of 500 mL. In Ca(OH)2 media, 0.50 g of argentian lead jarosite were used in an initial volume of 2 L to prevent CaSO4 saturation. The same conditions were used for the cyanidation study. OH- concentration was calculated by taking pH and ionization constant of water at working temperature as a base [22]. As in previous works [7, 10, 20], the progress of the decomposition reaction was followed by sulfur analysis with an Inductively Coupled Plasma (ICP) spectrometer. For the cyanidation, the reaction progress was followed by silver analysis with an Atomic Absorption Spectrophotometer (AAS). Solids obtained at different conversion values were characterized by X-ray Diffraction (XRD), Scanning Electron Microscopy (SEM) and Energy-dispersive X-ray spectroscopy (EDS). Induction time 6, experimental rate constant (kexp), reaction order n and activation energy Ea were determined in all the experiments. With the obtained information, we conducted the kinetic modeling of the alkaline decomposition and cyanidation of the argentian lead jarosite. Tables 1, 2 and 3 summarize the conditions and the data obtained experimentally, which were used for the kinetic modeling proposed in this paper.
References
1. Dutrizac, J. E.; Kaiman, S. Can. Mineral. 1976, 14, 151-158. [ Links ]
2. Smith, A. M. L.; Dubbin, W. E.; Wright, K.; Hudson-Edwards, K. A. Chem. Geol. 2006, 229, 344-361. [ Links ]
3. Patiño, F.; Ramírez, J. Rev. Soc. Quim. Mex. 1993, 37, 51-62. [ Links ]
4. Hendricks, S. B. Am. Mineral. 1973, 22, 773-784. [ Links ]
5. Dutrizac, J. E. Metall. Trans. 1983, B 14B, 531-539. [ Links ]
6. Patiño, F. PhD Thesis: “Cinetica de la cianuración de argento-jarosita y sus soluciones solidas con plumbojarosita”, Universitat de Barcelona, Facultat de Quimica, Espana, 1991. [ Links ]
7. Patiño, F.; Reyes, I.; Rivera I.; Reyes, M.; Hernández, J.; Pérez, M. J. Mex. Chem. Soc. 2011, 55, 208-213. [ Links ]
8. Patiño, F.; Salinas, E.; Cruells, M.; Roca, A.; Hydrometallurgy 1998, 49, 323-336. [ Links ]
9. Salinas, E.; Cerecedo, E.; Patiño, F.; Pérez, M. Metall. Trans. 2012, B H3B, 1027-1033. [ Links ]
10. Roca, A.; Cruells, M.; Patiño, F.; Rivera, I.; Plata, M. Hydrometallurgy 2006, 81, 15-23. [ Links ]
11. Cruells, M.; Roca, A.; Patiño, F.; Salinas, E.; Rivera, I. Hydrometallurgy 2000, 55, 153-163. [ Links ]
12. Patiño, F.; Roca, A.; Reyes, M.; Cruells, M.; Rivera, I. J. Mex. Chem. Soc. 2010 54, 216-222. [ Links ]
13. Patiño, F.; Yta, M.; Córdoba, D.A. Rev. Soc. Quim. Mex. 1996, 40,61-73. [ Links ]
14. Reyes, I.A.; Patiño, F.; Rivera, I.; Flores, M. U.; Reyes, M.; Hernandez, J. J. Braz. Chem. Soc. 2010, 22, 2260-2267. [ Links ]
15. Flores, M. U.; Patiño, F.; Reyes, I. A.; Rivera, I.; Reyes, M.; Juárez, J. C. J. Braz. Chem. Soc. 2012, 23, 1018-1023. [ Links ]
16. Russel, C.; Neel, C.; Bril, H. Sci. Total Environ. 2000, 263, 209-219. [ Links ]
17. Dutrizac, J. E.; Jambor, J. L. Formation and characterization of argentojarosite and plumbojarosite and their relevance to metallurgical processing. In: W.C. Park, D.M. Hausen and R.D. Hagni (Editors); Applied Mineralogy. AIME, Warrendale, Pa. 1984, 507-530. [ Links ]
18. Dutrizac, J. E. Jarosite-type compounds and their application in the metallurgical industry. In: K. Osseo-Asare and J.D. Miller (Editors), Hydrometallurgy, Research, Development and Plant Practice. TMS-AIME, Warrendale, Pa. 1982, 531-551. [ Links ]
19. Dutrizac, J. E.; Jambor, J. L. Trans. Inst. Min. Metall., 1987, C 96C, 206-218. [ Links ]
20. Patiño, F.; Vinals, J.; Roca, A.; Núnez, C. Hydrometallurgy 1994, 34, 279-291. [ Links ]
21. Canales, J. J. PhD Thesis: “Sintesis, descomposicion y cianuración de la jarosita de plomo argentífera en medio NaOH”, Universidad Autonoma del Estado de Hidalgo, A.A.C.T. y M., Mexico, 2009. [ Links ]
22. Lide, D. R. Handbook of chemistry and physics, Eds. CRC Press, Boston, 2009, 8-79. [ Links ]
23. Patiño, F.; Cruells, M.; Roca, A.; Salinas, E.; Pérez, M. Hydrometallurgy 2003, 70, 153-161. [ Links ]
24. Sohn, H. Y.; Wadsworth, M. E. Cinética de los procesos de la Metalurgia Extractiva, Ed. Trillas, México, 1986, 167-194. [ Links ]
25. Ballester, A.; Verdeja, L. F.; Sancho, J. Metalurgia Extractiva, Vol. 1. Fundamentos, Editorial Síntesis, Madrid, 2000, 182-189. [ Links ]
26. Levenspiel, O. Ingeniería de las Reacciones Químicas, Editorial Reverte, España, 2005, 393-448. [ Links ]