Artículo

 

The Electrodonating and Electroaccepting Powers in Atoms

 

Ángel Ulises Orozco-Valencia and Alberto Vela*

 

Departamento de Química, Cinvestav. Av. Instituto Politécnico Nacional 2508, Colonia San Pedro Zacatenco 07360, México D.F., México. avela@cinvestav.mx

 

Received February 02, 2012.
Accepted April 02, 2012.

 

Abstract

The derivations that lead to the introduction of the electro-philicity and of the electrodonating and electroaccepting powers are revisited. Special emphasis is given to the role played by the chemical potential of the bath in the definition of these global reactivity indexes. An alternative explanation to the increase of the energy when the system donates electrons is provided. It is also shown that the 2-parabolas model correctly predicts that there is no electron flow when the chemical potential of the bath, μ, is in the interval μ^- < μ < μ⁺, in almost complete consonance with the ensemble theorem at 0 K. The electrodonating and electroaccepting powers of neutral atoms in the Periodic Table are evaluated and used to explain how the values of these indexes will distribute in the electrodonating-electroaccepting powers plane.

Key words: Chemical Reactivity Theory, Conceptual DFT, Electro-philicity, Electroaccepting Power, Electrodonating Power, Periodic Behavior, Neutral Atoms.

 

Resumen

Se examinan las derivaciones que llevan a la introducción de la electrofilicidad y de los poderes electrodonadores y electro-aceptores. Se presta especial atención al papel que juega el potencial químico del baño en la definición de estos índices globales de reactividad. Se proporciona una explicación alternativa al incremento de la energía cuando el sistema dona electrones. También se muestra que el modelo de las dos parábolas predice correctamente que no hay flujo de electrones entre el sistema y el baño cuando el potencial químico del baño, μ, se encuentra en el intervalo μ^- < μ < μ⁺, en acuerdo casi completo con el teorema del ensamble a 0 K. Los poderes electrodonadores y electroaceptores de los átomos neutros en la tabla periódica se evaluaron y utilizaron para explicar cómo se distribuyen estos índices en el plano de poder electrodonador-poder electroaceptor.

Palabras clave: Teoría de reactividad química, teoría de funcionales de la densidad conceptual, electrofilicidad, poder electroceptor, poder electrodonador, comportamiento periódico, átomos neutros.

 

Introduction

The electrodonating and electroaccepting powers were introduced by Gazquez, Cedillo and Vela [1] to extend the definition of electrophilicity, a global reactivity coefficient, introduced by Parr, Von Szentpaly and Liu [2] which in turn was inspired on the work by Maynard et al. [3]. The electrophilicity has become an important chemical concept that has increased the number of tools available in Chemical Reactivity Theory (CRT)[4-6] to help explaining the vast world of chemical phenomena. The importance of electrophilicity can be appreciated by noting that despite its youth, it has already been reviewed several times [79]. Even though the appearance and usages of electrophilicity is not free of controversy [10, 11], in recent years electrophilicity and the electrodonating and electroaccepting powers have been used as descriptors of several and diverse chemical situations [12-27]. The definition of electrophilicity provided by Parr et al. [2] rests in the very well known and widely used model where the energy of a system is considered to be a continuous and differentiable function of the number of electrons [28]. In this model, that will be called the 1-parabola or the Parr-Pearson (PP) model, the differentiability assumption implies that the response of a chemical species to the processes of donating or accepting charge are the same. Even though the PP model is in conflict with the ensemble theorem [29], in its almost 30 years of existence it has proved to be extremely useful to explain and understand several chemical concepts and principles. In an effort to circumvent the differentiability issue, Gazquez, Cedillo and Vela [1] proposed a 2-parabolas model that led to the definition of the electrodonating and electroaccepting powers. This model will be called the GCV model. The GCV model incorporates the non-differentiability of the energy at an integer number of electrons by assuming that it has a quadratic behavior for fractional occupancies. This assumption does not fully comply with the ensemble theorem, but it captures an essential aspect of charge transfer of a species with an integer number of electrons, namely, that it depends on the direction of flow or, in more plain language, that receiving electrons is different from giving them away.

In this work, and for the sake of completeness, a brief review of the ensemble theorem and the 1-parabola (PP) model are presented first, followed by a more detailed presentation of the 2-parabolas (GCV) model, putting special emphasis in the important role played by the particle reservoir or electron bath in the definition of the electrodonating and electroaccepting powers. It will be shown that the GCV model recovers several consequences of the ensemble theorem that were not fully shown in the original derivation, and provides a better understanding of the physical meaning of these new global reactivity coefficients. The last contribution of this work is to present an analysis of the behavior of the electrodonating and electroaccepting powers in neutral atoms, addressing the issue of the relation between these indexes and the identification of the regions in the electroaccepting-electrodonating plane where one can locate species with different combinations of electronegativity and hardness.

 

The Ensemble Theorem

A fundamental theorem of electronic structure theory is the ensemble theorem [29-31] that states that at 0 K, the dependence of a size consistent property P with the number of electrons is given by the expression

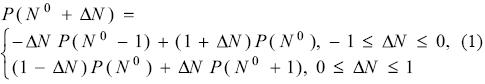
where N⁰ is a positive integer and ΔN is the change in the number of electrons. Eq. (1) simply tells that the function P(N) is a continuous function of the number of electrons and it is formed by a series of straight lines connecting the values of the property at the corresponding integer number of electrons. From Eq. (1), the derivative of this property with respect to the number of electrons is

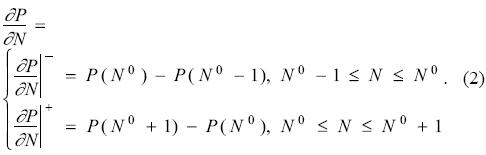
This expression establishes that, unless the property is a constant, the derivative of this quantity with respect to the number of electrons is discontinuous at all positive integers. For the case of the energy and when the number of electrons N⁰ corresponds to the electrically neutral system, the derivative is the chemical potential μ, and from Eq. (2) one has the very well known result

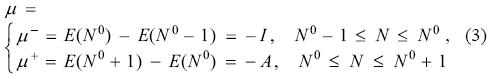
where I is the first vertical ionization potential and A is the vertical electron affinity. For the sake of clarity, even though the notation is self explanatory, the minus (-) superscript indicates the derivative taken from the left of N⁰ and the plus (+) for the right derivative. In physical terms, for a neutral system, the left derivative corresponds to the cationic branch while the right derivative to the anionic.

 

The 1-parabola (Parr-Pearson) model

In 1983, Parr and Pearson [28] introduced a model considering that the change of the energy of a system with respect to the change in the number of electrons ΔN is given by

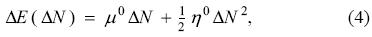
where

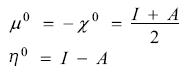
expression that is justified from the Taylor series expansion of the energy as a function of the number of electrons and a functional of the external potential, when the external potential is constant and one keeps terms up to second order; the quantities μ⁰, η⁰ and χ⁰ are the chemical potential, global hardness and electronegativity, respectively, of the reference system, and I and A have the same meaning as in the previous section. The model provided by Eq. (4) is the 1-parabola or the Parr-Pearson (PP) model. It must be noted that the definition of hardness used in this work does not include the factor of ½ originally used by Parr and Pearson. In Eq. (4) one is making a crucial assumption: the energy is a continuous and differentiable function of the number of electrons, assumption that is in contradiction with the ensemble theorem described in the previous section. Putting this very important fact aside, Parr and Pearson showed that Eq. (4) provides one way to prove the very well known chemical principle of electronegativity equalization and serves as the starting point to justify the principle of hard and soft acids and bases [32]. In brief, even with its evident flaw, the model proved to be an invaluable tool to understand and justify many well known but empirical facts of Chemistry. Under this model, consider a system that is in contact with a reservoir of electrons (bath) that has a chemical potential μ. On doing this, there will be a charge transfer process that is driven by the grand potential

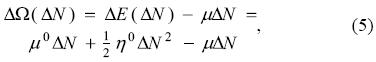
and, for a given chemical potential of the bath, the amount of electrons transferred is obtained by minimizing Eq. (5) with respect to ΔN. The solution of the equation ∂ΔΩ / ∂ΔN = 0, is

The change of energy associated with this charge transfer that minimized the grand potential is

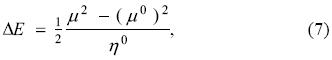
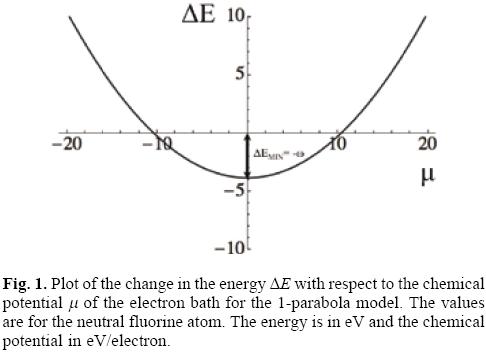
which is a concave upward parabola like the one depicted in Figure 1. Clearly, when the chemical potential of the bath is zero the energy change of the system is the most negative, i. e., it is a minimum, and from Eqs. (6) and (7), it corresponds to a change in the number of electrons and energy given by

and

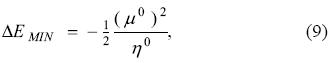
respectively. Note that these two quantities become independent of the properties of the surroundings (bath) and depend, solely, on characteristics of the system. Eq. (9) motivates the definition of the electrophilicity as

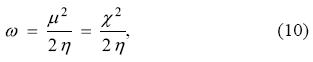
where χ is the electronegativity and where the superscript 0 has been dropped. Thus, electrophilicity can be interpreted as the negative of the minimum energy change that a chemical system attains when it is in contact with a reservoir of electrons and, as it was described above, this minimum is reached when the chemical potential of the bath is exactly zero, fact that was used by Parr, et al. [2] in the original derivation. According to this definition, the most electronegative and/or softer systems will become more stable by transferring charge from the bath of electrons than those that are less electronegative and/or harder.

 

The 2-parabolas (Gázquez-Cedillo-Vela) model

The model of the previous section assumes that the energy is a continuous and differentiable function of the number of electrons, which is in conflict with the ensemble theorem. This fact has a tremendous impact in any charge transfer process because it establishes that the amount of electrons transferred in a chemical event is not the same when the system is donating or receiving electrons. (s it was mentioned before, the incorporation of this fact was one of the motivations to introduce the 2-parabolas model. In this model, the change in the energy associated with a charge transfer event is written as

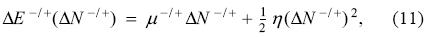
where the superscripts are used to distinguish the direction of charge transfer: minus (-) for the case of donation, and plus (+) for the acceptance of electrons; the chemical potentials μ^- and μ⁺ are introduced to discern between the left and right derivatives, respectively. This model does not comply completely with the ensemble theorem since the energy is not a set of straight lines but a set of parabolas. However, it captures one of its fundamental consequences, namely, that charge transfer distinguishes the direction of electron flow. Proceeding in a similar way as was done with the PP model, and considering that the system is in contact with an electron reservoir with chemical potential μ, then, the direction of charge flow is governed by the grand potential

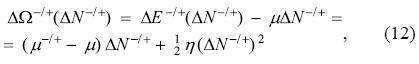
and the charge transferred between the system and the bath is obtained minimizing ΔΩ^-/+ with respect to the amount of transferred electrons ΔN^-/+. This minimization leads to

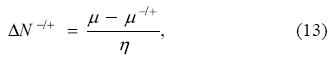
expression that reduces to the 1-parabola result when μ^- = μ⁺ = μ⁰, which simply corresponds to the assumption of differentiability of the energy with respect to the number of electrons. Note that to avoid a cumbersome notation, in this section the superscript 0 has been dropped in the expressions for μ^-, μ⁺, and η, but they correspond to the right and left first derivatives, and to the second derivative, respectively, when one approaches the corresponding integer number of electrons N⁰. Substituting Eq. (13) in Eqs. (11) and (12), one obtains that the change of the energy and grand potential are given by:

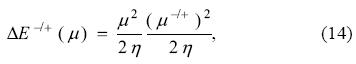
and

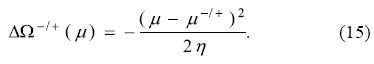
Analogously to the PP model, it is clear from Eq. (14) that the minimum attainable energy is obtained when the chemical potential of the bath is zero, and this minimum energy is

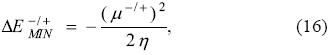
which justifies the introduction (definition) of the electrodonat ing (ω^-) and electroaccepting powers:

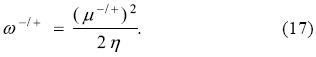
With these two global reactivity indexes the minimum energy attained by a system interacting with a bath of electrons can be simply expressed as

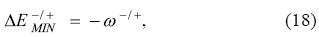
where it is clear that the change in energy is different for the two possible directions of electron flow. The physical interpretation of the electrodonating and electroaccepting powers goes parallel to that of the PP model: they are the lowest attainable energies of a system in contact with an electron reservoir when one distinguishes between the directions of electron transfer.

One last ingredient is necessary to complete this model and it is an assumption regarding the global hardness. From the ensemble theorem [see Eq. (3)] it is possible to write the first derivative of the energy with respect to the number of electrons, i.e., the chemical potential, as

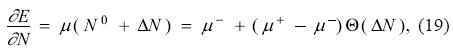
where Θ(x) is the Heaviside step function. Taking the derivative of Eq. (19) with respect to the number of electrons and using the fact that the derivative of the Heaviside function is a Dirac delta function δ(x), one is lead to

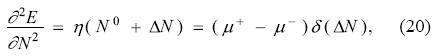
which establishes that the second derivative of the energy is zero, when the number of electrons is fractional, and diverges, for all integer numbers of electrons. One cannot use Eq. (20) in a continuous model, like GCV, but it can be used as a justification to suggest that the hardness of the model is related to the left- and right-derivatives by

which constitutes the last assumption of the GCV model.

Evaluating Eq. (11), for ΔN^- = -1 and ΔN⁺ = 1, which correspond to ΔE^- = I and ΔE⁺ = -A, respectively, and using Eq. (21), one obtains that the left- and right-chemical potentials in terms of the ionization potential and electron affinity are given by

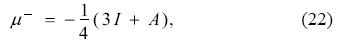
and

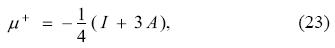
expressions originally derived in the GCV model. Substituting Eqs. (22) and (23) in Eqs. (17) and (21) lead to the expressions for the electrodonating and electroaccepting powers in terms of the ionization potential and the electron affinity [see Eqs. (12) and (13) of reference 1]. It is worth to underline that one important difference between the GCV model and the ensemble theorem rests, precisely, in Eqs. (22) and (23), which are different from those predicted by the ensemble theorem and given by Eqs. (3). In this vein, one could be tempted to use Eqs. (3) in the definitions of the electrodonating and electroaccepting powers, however, this is incorrect since the only way to recover the ensemble theorem results is abandoning the quadratic nature of the model.

One can gain a better understanding of the physical implications of the model by plotting the changes in the energy and the grand potential as functions of the chemical potential of the bath, as depicted in Figures 2 and 3, where a particular atom is used, fluorine in this case, but the results are general. A first feature to be noted from Figure 2 is that the change in the energy for the donating (-, red curve) process is more negative than that corresponding to the acceptance of electron charge (+, blue curve). This reflects the fact that more energy is required to extract an electron from a neutral system than from an anion, or that the successive ionization potentials have the order ··· < I_N+2 < I_N+1 < I_N < L. On can also note that there are intervals of the chemical potential of the bath where the charge flow helps to stabilize energetically the system. Thus, ΔE ^-/+ < 0 in the intervals -μ^-/+ < μ < μ^-/+ that correspond to the donation/acceptance (red/blue curve) of electrons to/from the particle bath. The most important feature related to the definition of the electrodonating and electroaccepting powers is that, independently of the direction of electron flow and from an energetic point of view, the situation where the system becomes more stable is when the chemical potential of the bath is null (μ = 0). These minimum energies are shown in Figure 2 and are used to emphasize their relation with the definition of the electrodonating and electroaccepting powers.

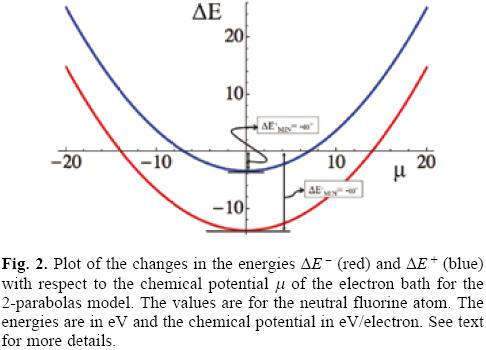
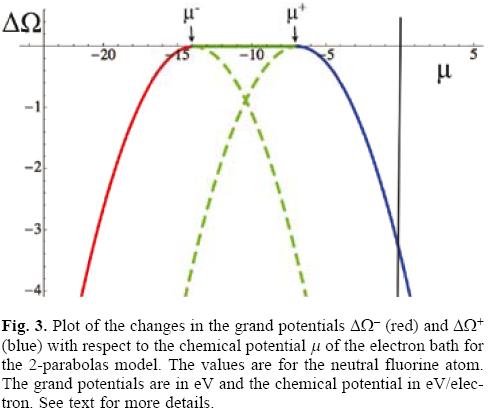
Figure 3 has several very interesting implications that, in the authors' opinion, were not fully exploited in the original GCV presentation of ω^-/+. The grand potentials of the GCV model corresponding to the donation and acceptance of electrons from the reservoir are depicted in Figure 3. The first aspect that must be appreciated is that both grand potentials are always negative, indicating that the transfer of electrons between the system (an open quantum system) and the reservoir is a process that always occurs spontaneously. The green dashed branches are situations where the electron flow violates its natural direction and, consequently, must be neglected from the model. To appreciate this more clearly one can plot the change in the number of electrons associated to each process as a function of the chemical potential of the bath, as depicted in Figure 4.

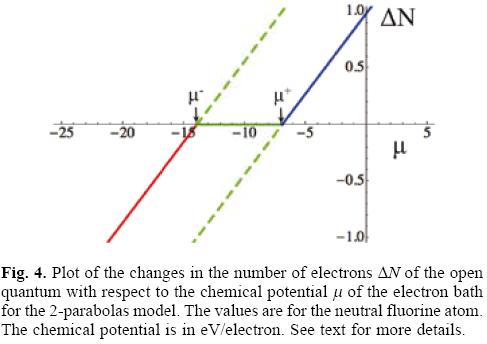
The straight lines shown in Figure 4 correspond to those obtained by Eq. (13), and they can also be derived by using the fact that the grand potential is the Legendre transform of the energy with respect to the chemical potential and, consequently, that ∂ΔΩ/∂μ = -ΔN, which together with Eq. (15) leads to Eq. (13). The slopes of both straight lines are the same (they are parallel) and equal to the softness of the system S = 1/η, and they cross the μ-axis at μ = μ^-/+, points marked by the small vertical arrows in figure 4. Considering these facts and assuming that the model satisfies the inequality μ^- < μ⁺, which follows from the satisfaction of I > A and Eq. (3), one can identify the line at the extreme left in figure 4 with the donation process and the right one with the acceptance of electrons. Focusing on the left line, it is evident that for μ < μ^- (the red line segment in Figure 4) the number of electrons transferred ΔN is negative but, for μ > μ^- (the dashed green segment, continuation of the red segment) ΔN is positive, result that is in conflict with the expected direction of electron flow. A similar analysis can be done with the accepting process except that in this case the conclusion is that the segment with physical reality is the solid blue segment that corresponds to the situation when the chemical potential of the bath satisfies that μ > μ⁺, and the dashed green segment has to be discarded. Thus, coming back to the grand potential depicted in Figure 3, the previous analysis allows one to discard the dashed green segments of the two parabolas and to establish that the change of the grand potential of the GCV model consists of the solid red, solid green and solid blue segments. Physically, the solid green horizontal line predicts that when the chemical potential of the bath is in the interval μ^- < μ < μ⁺ there is no flow of electrons between the open system and the electron reservoir. This fact is in partial agreement with the prediction from the ensemble theorem; partial, because the model assumes the existence of the second derivative of the energy with respect to the number of electrons which in turn implies that μ^- ≠ - I and μ⁺ ≠ - A, as was already noted above.

 

Relation between ω^- and ω⁺

As it was mentioned in the Introduction, the electrodonating and electroaccepting powers have been used to try to rationalize several aspects of chemical reactivity, especially as an aid to classify the behavior of several substances as potential antioxidants or radical scavengers [17, 19-22]. Some of these attempts have proposed the usage of plots of ω^- vs. ω⁺, and indeed it has been possible to identify families of substances that will behave in a similar fashion. In this section it is shown that some of the observed behavior can be explained by means of the results presented in the previous section and the intention is to provide guidelines for a better understanding of this kind of plots.

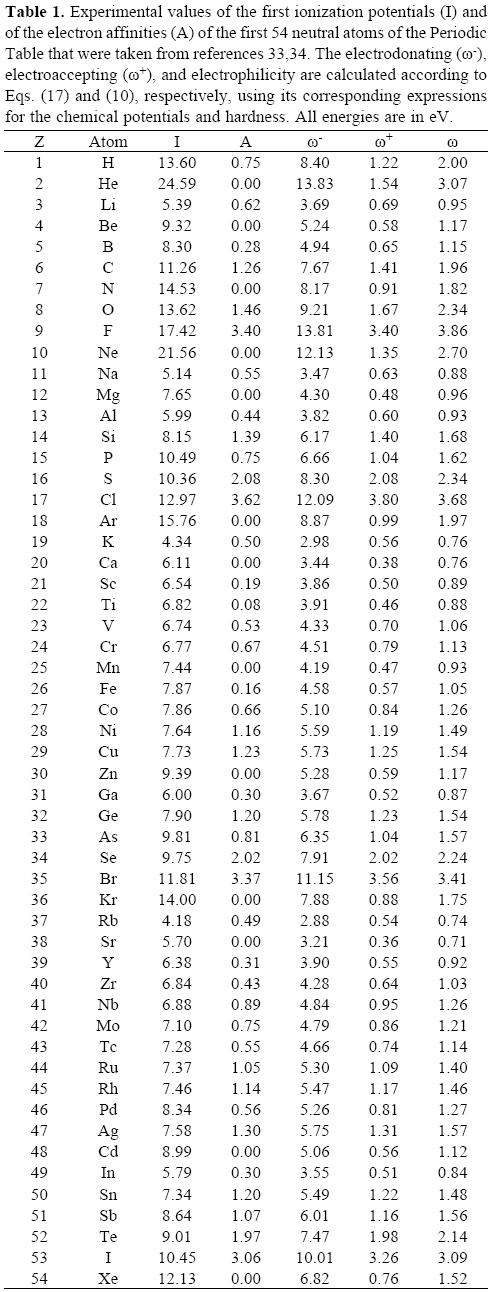
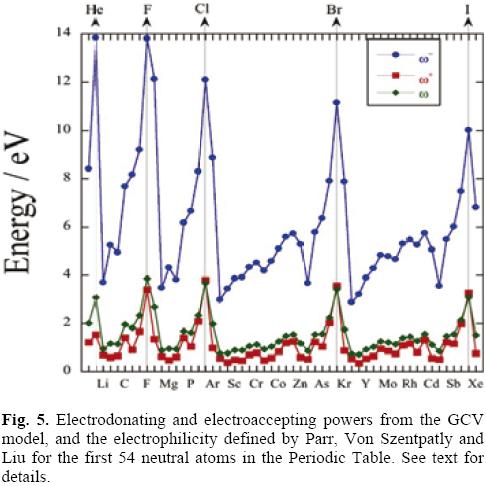
Since very reliable experimental information about the first ionization potentials and the electron affinities of neutral atoms is available in the literature [33, 34] the discussion herein presented is limited to these systems. The data used to obtain the plots of this section is presented in Table 1. Surprisingly, even though the electrophilicity, and the electrodonating and electroaccepting powers have been evaluated for atoms, to the authors' knowledge, the only attempt to discuss its periodic behavior is that of reference [35]. The behavior of the electrodonating and electroaccepting powers, together with the electrophilicity is depicted in Figure 5. The first feature to be noted is that, as it was predicted in the previous section, the electrodonating power of an atom is always larger than the electroaccepting power, difference that reflects the fact that the ionization potential is larger than the electron affinity. One can also see that the periodic behavior of the electroaccepting power is very similar to that of the electrophilicity. Within a row of the Periodic Table, the maximum value of these three global reactivity indexes is found for the halogens, with the addition of Helium. This observation allows one to establish that halogens are the neutral atoms that become more stable when they accept charge from the electron reservoir, and more unstable when they give away electrons to the bath. Contrasting with the maxima, the minima values within a row are different. The minima in the electrodonating power are found for the alkaline metals and in the alkaline-earth metals for the case of the electroaccepting power. This means that alkaline metals are not stabilized much when they receive electrons while the halogens become much more stable taking electrons from the bath, situation that agrees with the known behavior of these elements. Care should be taken in the interpretation of ω^- because, as it was explained in the previous section, this channel of charge transfer is not active until the chemical potential of the bath is less or equal than μ^-, and as Eq. (14) predicts all transfer of electrons from the open quantum system to the bath are energetically unfavorable. Thus, when one is seeking for systems with good electrodonating capabilities, one should look for systems with small ω^-. That is, the lower the electrodonating power the better its donation capabilities will be.

The foregoing discussion does not invalidate to try to establish a relation between ω^- and ω⁺. To this end, consider expressing these reactivity indexes in terms of the electronegativity, χ, and the hardness, η, namely,

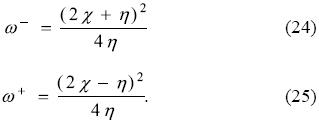
Since I > A, the electronegativity and the global hardness are positive and then, from Eqs. (24-25) one has that ω^- > ω⁺, as it has been mentioned several times before. These last equations also allow one to establish that the relation between the electrodonating and electroacepting powers is given by

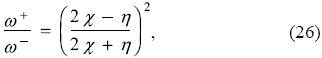
indicating that the plot of ω⁺ vs. ω^- is a line that crosses the origin with slopes given by Eq. (26). To identify regions where systems of a given class will be located in the ω⁺ - ω^- plane one can use Eq. (26) that suggests the existence of the following 4 classes:

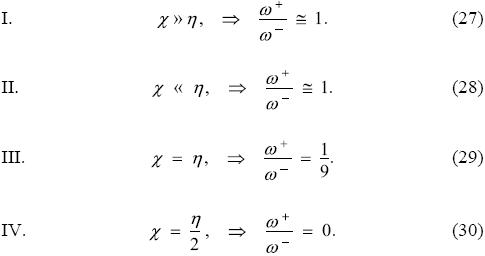
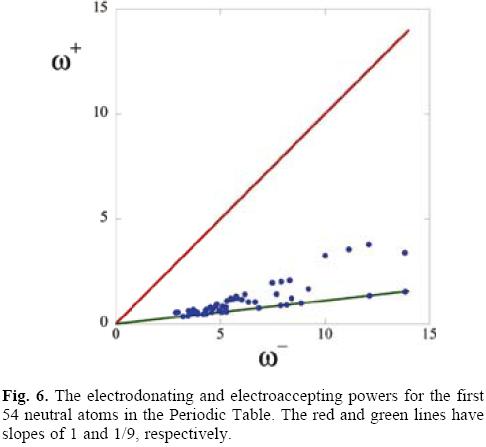
Classes I and II show that sets of systems that are much more electronegative than hard or that are much more harder than electronegative cannot be distinguished and will be located along the line with a slope of 45° in the ω⁺ - ω^- plane. Systems belonging to class III are those with very similar electronegativities and hardnesses; these systems lie along the line with a slope of approximately 6.3° and, from the relation between hardness and electronegativity with the first ionization potential and electron affinity, one can see that the systems belonging to this class are those with null electron affinities like the noble gases, closed shells and half-filled shells. Class IV determines the condition needed for systems to lie in the horizontal axis, and one does not expect to have systems lying in this line because the electron affinities corresponding to this line are negative. Finally, it is important to recall that the condition ω⁺ < ω^- implies that the only region of the ω⁺ - ω^- plane that will be occupied is the lower half triangle of the first quadrant. To support the preceding analysis, the electrodonating and electroaccepting powers of the neutral atoms in the Periodic Table in the ω⁺ - ω^- plane are depicted in Figure 6. In this Figure, the red line corresponds to systems belonging to cases I and II, described above, the green line to those of class III, and the horizontal (ω^-) axis to class IV. As expected, most of the neutral atoms cluster in the region between the red and green lines. There is no unique line correlating these two global indexes, fact that supports the idea that one should try to group systems having a common characteristic, like the conditions used in the classes described above, before attempting any correlation of these properties.

 

Conclusions

In this contribution we have revisited the derivations of the electrophilicity introduced by Parr, et al. [2] and of the electrodonating and electroaccepting powers introduced by Gázquez, et al. [1], focusing on a presentation where one considers the system under study as an open quantum system in contact, and in equilibrium, with a reservoir of electrons. As it was shown, there are no new results but, in the authors' opinion, this presentation clarifies some aspects of the original derivations of these reactivity indexes. The approach presented here has shown why, in both models, the definitions of these global reactivity coefficients appear naturally when the chemical potential of the bath is zero, and it also provides an explanation to the fact that in the 2-parabolas model the change in the energy of the system, when it is donating electrons to the bath, is always positive. It has also been realized that the GCV model accounts for the fact that at 0 K an open quantum system in equilibrium with a bath of electrons has no electron transfer when the chemical potential of the bath, μ, is in the interval μ^- < μ^- < μ⁺, in almost full agreement with the exact result. The quadratic nature of the model manifests itself with the fact that -μ^- and -μ⁺ are different from the ionization potential and electron affinity, respectively. To explore in more detail the nature of the electrodonating and electroaccepting powers, its behavior for the first 54 neutral atoms in the Periodic Table was analyzed and was used to rationalize the distribution of systems in the ω⁺ - ω^- plane. The authors hope that the results of this work will encourage more researchers to use these global reactivity coefficients in their attempts to correlate observed chemical behavior with molecular properties.

 

Acknowledgements

It is an honor and a pleasure to contribute to this special issue dedicated to Prof. José Luis Gàzquez. We celebrate the achievements of Prof. Gàzquez in Density Functional Theory, particularly in Chemical Reactivity Theory. And we also celebrate that we had the opportunity of being his students, colleagues, but most of all, his friends. AUOV thanks Conacyt for a doctoral fellowship. This works was partially funded by Conacyt project # 128369.

 

References

1. Gazquez, J. L.; Cedillo, A.; Vela, A. J. Phys. Chem. A 2007, 111, 1966.         [ Links ]

2. Parr, R. G.; von Szentpaly, L.; Liu, S. B. J. Am. Chem. Soc. 1999, 121, 1922.         [ Links ]

3. Maynard, A. T.; Huang, M.; Rice, W. G.; Covell, D. G. Proc. Natl. Acad. Sci. USA 1998, 95, 11578.         [ Links ]

4. Chermette, H. J. Comput. Chem. 1999, 20, 129.         [ Links ]

5. Gazquez, J. L. J. Mex. Chem. Soc. 2008, 52, 3.         [ Links ]

6. Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103, 1793.         [ Links ]

7. Chattaraj, P. K.; Sarkar, U.; Roy, D. R. Chem. Rev. 2006, 106, 2065.         [ Links ]

8. Chattaraj, P. K.; Roy, D. R. Chem. Rev. 2007, 107, PR46.         [ Links ]

9. Chattaraj, P. K.; Giri, S.; Duley, S. Chem. Rev. 2011, 111, PR43.         [ Links ]

10. Mayr, H.; Breugst, M.; Ofial, A. R. Angew. Chem. Int. Edit. 2011, 50, 6470.         [ Links ]

11. von Szentpaly, L. J. Phys. Chem. A 2011, 115, 8528.         [ Links ]

12. Chamorro, E.; Chattaraj, P. K.; Fuentealba, P. J. Phys. Chem. A 2003, 107, 7068.         [ Links ]

13. Elango, M.; Parthasarathi, R.; Narayanan, G. K.; Sabeelullah, A. M.; Sarkar, U.; Venkatasubramaniyan, N. S.; Supramanian, V.; Chattaraj, P. K. J. Chem. Sci. 2005, 117, 61.         [ Links ]

14. Roy, D. R.; Giri, S.; Chattaraj, P. K. Mol. Divers. 2009, 13, 551.         [ Links ]

15. Roy, D. R.; Parthasarathi, R.; Maiti, B.; Subramanian, V.; Chattaraj, P. K. Biorg. Med. Chem. 2005, 13, 3405.         [ Links ]

16. Roy, D. R.; Sarkar, U.; Chattaraj, P. K.; Mitra, A.; Padmanabhan, J.; Parthasarathi, R.; Subramanian, V.; Van Damme, S.; Bultinck, P. Mol. Divers. 2006, 10, 119.         [ Links ]

17. Martinez, A.; Rodriguez-Girones, M. A.; Barbosa, A.; Costas, M. J. Phys. Chem. A 2008, 112, 9037.         [ Links ]

18. Moens, J.; Jaque, P.; De Proft, F.; Geerlings, P. J. Phys. Chem. A 2008, 112, 6023.         [ Links ]

19. Martinez, A. J. Phys. Chem. B 2009, 113, 4915.         [ Links ]

20. Martinez, A. J. Phys. Chem. B 2009, 113, 3212.         [ Links ]

21. Martinez, A.; Rodriguez-Girones, M. A.; Barbosa, A. Ardeola 2009, 56, 287.         [ Links ]

22. Martinez, A.; Vargas, R.; Galano, A. J. Phys. Chem. B 2009, 113, 12113.         [ Links ]

23. Galano, A.; Narciso-Lopez, M.; Francisco-Márquez, M. J. Phys. Chem. A 2010, 114, 5796.         [ Links ]

24. Martinez, A. J. Phys. Chem. C 2010, 114, 21240.         [ Links ]

25. Martinez, A.; Alonso, J. C.; Sansores, L. E.; Salcedo, R. J. Phys. Chem. C 2010, 114, 12427.         [ Links ]

26. Ramirez-Ramirez, J. Z.; Vargas, R.; Garza, J.; Gazquez, J. L. J. Phys. Chem. A 2010, 114, 7945.         [ Links ]

27. Valdespino-Saenz, J.; Martinez, A. J. Mol. Struct.-Theochem 2010, 939, 34.         [ Links ]

28. Parr, R. G.; Pearson, R. G. J. Am. Chem. Soc. 1983, 105, 7512.         [ Links ]

29. Perdew, J. P.; Parr, R. G.; Levy, M.; Balduz, J. L. Phys. Rev. Lett. 1982, 49, 1691.         [ Links ]

30. Ayers, P. W. J. Math. Chem. 2008, 43, 285.         [ Links ]

31. Yang, W. T.; Zhang, Y. K.; Ayers, P. W. Phys. Rev. Lett. 2000, 84, 5172.         [ Links ]

32. Ayers, P. W. Faraday Discuss. 2007, 135, 161.         [ Links ]

33. Hotop, H.; Lineberger, W. C. J. Phys. Chem. Ref. Data 1985, 14, 731.         [ Links ]

34. Moore, C. E. Ionization potentials and ionization limits derived from the analyses of optical spectra, National Bureau of standars; NSRDS-NBS, 1970, 34, IV, 8.         [ Links ]

35. Islam, N.; Ghosh, D. C. Int. J. Quantum Chem. 2011, 111, 3556.         [ Links ]

 

Note

* The asterisk indicates the name of the author to whom inquires about the paper should be addressed.