Artículo

 

MCSCF-MRMP2 and DFT Exploratory Study on the Stability of Possible Intermediates in the Ru(H₂O)₆²⁺ + H₂O₂ Reaction: Importance of the Multiconfigurational Character in the Description of the Ru=O Moiety

 

Ana Elizabeth Torres,¹ Thangarasu Pandiyan,² and Fernando Colmenares¹*

 

¹ Departamento de Física y Química Teórica, Facultad de Química, Universidad Nacional Autónoma de México. Ciudad Universitaria, México, D.F. 04510. México. colmen@unam.mx

² Departamento de Química Inorgánica y Nuclear, Facultad de Química, Universidad Nacional Autónoma de México. Ciudad Universitaria, México, D.F. 04510. México.

 

Received December 06, 2011.
Accepted April 02, 2012.

 

Abstract

MCSCF-MRMP2 and DFT calculations were performed in order to analyze the stability and geometrical parameters of some possible intermediates for the reactions Ru²+ + H₂O₂ and Ru(H₂O)₆²⁺ + H₂O₂. At MCSCF-MRMP2 level of calculation, the stability predicted for the Ru^IVO(H₂O)₅²+ suggests an energetic preference of the reaction Ru(H₂O)₆²⁺ + H₂O₂ toward the products involving this high-valence intermediate, in agreement with the commonly accepted mechanism for this kind of reactions. Due to its multiconfigurational character, the DFT approaches used in this work exhibited some limitations for properly describing the RuO^IV(H₂O)₅²+ ion and therefore the energy gap between the possible investigated intermediates.

Key words: MRMP2, DFT, Ruthenium oxo Compounds, Electron Correlation, Ru^IVO.

 

Resumen

Se realizaron cálculos a nivel MCSCF-MRMP2 and DFT con la finalidad de analizar la estabilidad y los parámetros geométricos de algunos intermediarios posibles para las reacciones Ru²+ + H₂O₂ and Ru(H₂O)₆²+ + H₂O₂. La estabilidad predicha a nivel MCSCF-MRMP2 para el ion Ru^IVO(H₂O)₅²+ sugiere una preferencia energética de la reacción Ru(H₂O)₆²+ + H₂O₂ por los productos asociados con este intermediario de alta valencia, en acuerdo con el mecanismo usualmente aceptado para este tipo de reacciones. Debido a su naturaleza multiconfiguracional, las aproximaciones basadas en la teoría de funcionales de la densidad utilizadas en esta investigación exhibieron algunas limitaciones para describir adecuadamente el ion RuO^IV(H₂O)₅²+ y, por tanto, la diferencia de energía entre los posibles intermediarios investigados.

Palabras clave: MRMP2, DFT, compuestos oxo de rutenio, correlación electrónica, Ru^IVO.

 

Introduction

The study of the reactions of H₂O₂ with transition metal compounds to yield powerful oxidizing intermediates represents an important research field both, experimentally and theoretically, due mainly to its applications in organic chemistry and catalysis [1, 2].

The Fenton mixture, consisting of an acidic aqueous solution of Fe²⁺ ions and hydrogen peroxide, is by far the most known example of this kind of reactions [3-10]. The equivalent mixture formed with ruthenium and H2O2 has been used to oxidize different organic compounds, such as phenol and cyclohexene. For this oxidizing mixture, high-valence Ru^IVO species is thought to be produced [11-13] and a mechanism involving high-valence intermediates, instead of radical species, is generally accepted (nevertheless, not conclusive arguments have been achieved yet on this regard; for some of these reactions a mechanism involving radical species cannot be ruled out). It is thought that Ru^IVO species generated in-situ could be responsible of the oxidant potential exhibited by these mixtures [14-16].

Therefore, with the aim of gaining some insight on the inherent preferential formation of intermediate species i.e. the high-valence moiety Ru^IVO²⁺ or the Ru^IIIOH²⁺ ion relating to the formation of the hydroxyl radical from the reaction of Ru²⁺ + H2O2 the relative stability of these species was analyzed by the MCSCF-MRMP2 calculations. Similarly, for the Ru^IVO(H₂O)₅²+ and Ru^IIIOH(H₂O)₅²+ ions shown in Figure 1, which could be the corresponding intermediates for the model reaction Ru(H₂O)₆²⁺ + H₂O_2> the relative stability was determined at the same level of calculation.

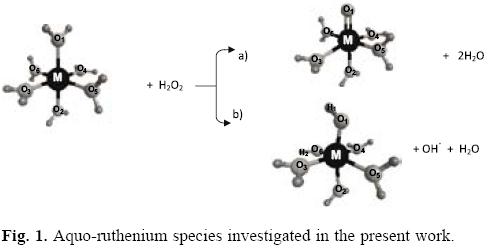
Recently, the performance of different combinations of exchange-correlation density functionals and basis sets for the calculation of geometrical parameters of some ruthenium complexes has been evaluated by Kulkarny and Truhlar [17]. Likewise, Zhao and Truhlar have analyzed comparatively the performance of different functionals in the description of systems of chemical interest, such as those involving multireference rearrangements, for which these authors recommend, among others, the use of the M06 functional instead of the widely used B3LYP [18]. Truhlar's group have also tested different functional and basis sets for the determination of the aqueous Ru³⁺/Ru²⁺ reduction potential [19]. In the present work, the energies of the singlet electronic states of the different aquo complexes are obtained by performing density functional theory calculations using the functional-basis set combinations B3LYP-LAN-L2DZ and M06-DEF2-TZVP and the results are compared with those emerging from the MCSCF-MRMP2 approach.

 

Results and Discussion

The Ru²⁺ + H₂O₂ reaction

In Figure 2 are shown the relative energies for the low-lying electronic states of the fragments Ru^IIIOH²⁺ + OH· and Ru^IVO²⁺ + H₂O. For both metallic moieties, Ru^IIIOH²⁺ and Ru^IVO²⁺, the energy of the highest spin electronic states lies below the ground state reference; furthermore, since the fragments associated with the Ru^IIIOH²⁺ ion are located at 18.7 kcal/mol below than that of the high-valence Ru^IVO²⁺ ion, thereby in this reaction the Ru^IIIOH²⁺ species could preferentially be formed. Yet, no conclusions can be attained in this sense, as the overall paths joining the reactants with these possible products (or intermediates) were not calculated in this work.

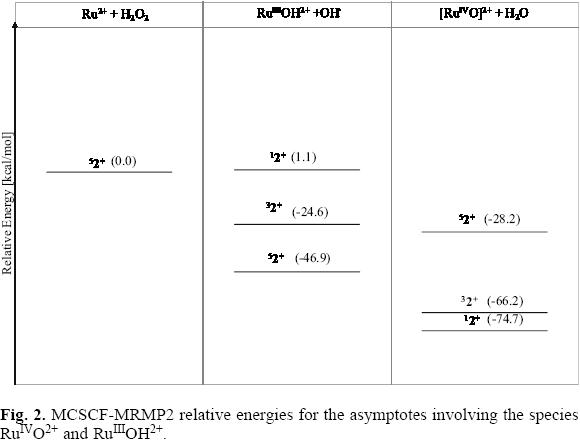
For the singlet fragments Ru^IIIOH²⁺ + OH, the calculated energy is above from the corresponding to the ground state of the reactants. However, for this multiplicity the energy of the species Ru^IVO²⁺ + H₂O is 74.7 kcal/mol below this reference; this value suggests a strong interaction between the oxygen and the metallic atom for the closed shell configuration of the Ru^IVO²⁺ ion. The Ru-O interaction at the lowest spin electronic state favors a shorter distance, 1.45 Å, than that detected for the high multiplicity state, 1.59 Å. The triplet state of the Ru^IVO²⁺ + H₂O exhibits a similar stability than the singlet one. Although also stable, the corresponding fragments Ru^IIIOH²⁺ + OH lie nearly 41 kcal/mol above the high valence intermediate asymptote.

Even though the singlet or triplet Ru^IVO²⁺ intermediates are not relevant when the reaction Ru²⁺ + H₂O₂ occurs following the quintuplet ground state, the great stability detected for the high-valence low multiplicity moieties could play an important role in the reaction of H₂O₂ with ruthenium compounds having a closed shell or a triplet ground state configuration.

 

Ru(H₂O)₆²⁺ + H₂O₂ reaction

MCSCF-MRMP2 energies for the singlet and quintuplet electronic states of the reactants Ru(H₂O)₆²⁺ + H₂O₂ as well as for the fragments involving the species Ru^IVO(H₂O)₅²⁺ and Ru^IIIOH(H₂O)₅²⁺ are shown in Figure 3. The triplet electronic states of these fragments were not considered in this study as the experimentally detected ground state for the reactants corresponds to the singlet multiplicity [20, 22]. Values for the DFT energies emerging from the B3LYP/LANL2DZ and M06/DEF2 calculations for the singlet structures of the aquo-complexes are provided in Figure 4. For comparison, in this figure are also included MCSCF-MRMP2/DEF2 energy values evolving from single-point calculations for the previously optimized singlet structures at the MCSCF level using the basis and pseudopotentials provided by LaJohn et al [25, 27, 28]. In Table 1 some relevant geometrical parameters for these ions are collected.

At MCSCF-MRMP2 level, the calculated energy difference between the singlet and quintuplet electronic states of the hexa-aquo ion is 18 kcal/mol (Figure 3), the low multiplicity state being more stable (in contrast to the detected energy order for these states in the bare ion Ru²⁺, as discussed before for the Ru²⁺ + H₂O₂ reaction). The greater stability found for the low spin complex is consistent with the experimental determinations made through UV-Visible spectroscopy on the hexa-aquo compound and it can be attributed to large ligand field effects [20, 22].

It is important to point out that inclusion of dynamical correlation plays a crucial role for obtaining a correct description of the electronic states of the haxa-aquo complex, as the energy value calculated for the low spin state at MCSCF level is higher than the corresponding to the quintuplet electronic state. Only after dynamic correlation was extensively included through MRMP2 single point calculations the energy values for these states were obtained consistently with the experimentally determined low-spin ground state.

The energy difference between these electronic states was previously reported by Åkesson et al. [23]. The value obtained by these authors through MRCI calculations (which included Davidson correction) for this energy gap is 3.4 kcal/mol, with the quintuplet state being more stable than the singlet one. To the best of our knowledge, this energy difference has not been reported by other authors.

The optimized geometry at MCSCF level (without symmetry restrictions) for the singlet ground state of the hexa-aquo molecule resembles nearly a structure corresponding to the D2h symmetry group. The calculated Ru-O bond distance (for the six equivalent metal-oxygen interactions), 2.14 Å, is in good agreement with the experimental value determined on dilute solutions through EXAFS experiments, 2.11 Å [21]. As shown in Table 1, for the high multiplicity electronic state slightly shorter equatorial than axial Ru-O bond distances were found (2.34 and 2.36 Á, respectively).

The DFT computed metal-oxygen bond lengths for the singlet ground state of the hexa-aquo ion are also in good agreement with the available experimental data with the best result obtained at M06-DEF2-TVZP level, 2.13 Å.

In accord to the energy values shown in the Figure 3, both the singlet and quintuplet electronic states of the fragments Ru^IIIOH(H₂O)₅²⁺ + H₂O + OH· (which correspond to the doublet and sextuplet electronic states of the ion Ru^IIIOH (H₂O)₅²⁺, respectively) are unstable. At MCSCF-MRMP2 level of theory the singlet state is found to be 14.9 kcal/mol above the ground state of the reactants, whereas the fragments corresponding to the high multiplicity state lie above the energy reference by near 70 kcal/mol. As it is seen in Figure 4, the energy values computed at B3LYP/LANL2DZ and M06/DEF2 levels for the low multiplicity state of these fragments are 24.3 and 11.6 kcal/mol, respectively. As it is also shown in this figure, the use of the basis set DEF2 does not have a significant effect on the calculated energy value at MCSCF-MRMP2 level for the hydroxo species (the energy difference is only 1.8 kcal/mol). However, it leads to a greater stabilization of the ruthenium oxo intermediate, as the calculated energy is nearly 9 kcal mol below the value provided in Figure 3 for this structure.

For the hydroxo complex the calculated Ru-O distances through the three levels of calculation were similar. The shorter value, 1.87 Å, is obtained from the M06/DEF2 calculation whereas the longer one, 1.89 Å, evolves from the remaining DFT-scheme calculation.

As depicted in Figure 4, a stable structure is predicted for the singlet electronic state of the fragments involving the high-valence oxo ion Ru^IVO(H2O)5²⁺ at MCSCF-MRMP2/DEF2 level. The energy value for this electronic state is 32.7 kcal/mol below the ground state of the reactants. The energy values in Figure 4 emerging from the DFT calculations for the singlet state of the fragments Ru^IVO(H₂O)₅²⁺ + 2H₂O are significantly higher than the MCSCF-MRMP2 value; the M06/DEF2 calculated energy lies below the ground state reference by 2.8 kcal/mol whereas the B3LYP/LANL2DZ value is 19.5 kcal/mol above the re-actants. Despite the variations in the calculated energy values for the penta-aquo oxo compound, a reasonable consistency is obtained for the predicted geometrical parameters for this high-valence ion at the three levels of theory. For instance, only minor differences were detected between the computed Ru=O bond lengths, the B3LYP/LANL2DZ distance, 1.74 Å, being slightly longer than those obtained at M06/DEF2 and MCSCF levels, 1.70 and 1.71 A, respectively. These values agree with the formal metal-oxygen double bond expected for this kind of high-valence ruthenium oxo compounds [24].

It is worth pointing out that the significant variations between the calculated energies of the high-valence species Ru^IVO(H₂O)₅²⁺ at the different theoretical approaches could have an important effect in the study of reaction profiles involving this oxo ion. For instance, at singlet electronic state, the MCSCF-MRMP2/DEF2 energy gap between the fragments involving the ions Ru^IIIOH(H₂O)₅²⁺ and Ru^IVO(H₂O)₅²⁺ is 45.8 kcal/mol (Figure 4). Although not conclusive, the significant difference in the stability predicted for these species suggests that the reaction Ru(H2O)6²⁺ with H2O2 could take place via the high-valence oxo intermediate Ru^IVO(H2O)5²⁺. This result is in agreement with the commonly accepted mechanism for this reaction [14-16]. According to Figure 4, values for this gap at B3LYP/LANL2DZ and M06/DEF2 levels are 4.8 and 14.5 kcal/mol, respectively.

The different stability predicted for the Ru^IVO(H2O)5²⁺ cation through the three levels of theory could be related to the multiconfigurational character exhibited by this oxo compound. The dominant contribution to the MCSCF expansion of the function describing the singlet ground state of the Ru^IVO(H2O)5²⁺ cation corresponds to the closed shell configuration (with a coefficient of 0.8). However, several contributions associated with open shell singlet electronic configurations (all of them involving interactions among the d-type orbitals of the metallic ion with the p orbitals of the oxygen involved in the RuO double bond) appear in this expansion with coefficients significantly greater than 0.1 (for instance, 0.26 and 0.48). Hence, a suitable description of the singlet electronic state of the metal oxo cation demands a multiconfigurational treatment which allows including these significant contributions (this character is not so important for the description of the Ru^IIIOH(H₂O)₅²⁺ ion, as the dominant configuration in the variational expansion corresponding to the doublet electronic state has a weight nearly to 0.97 and only two configurations have coefficients slightly greater than 0.1).

Mainly due to its monodeterminantal nature, DFT calculations could exhibit serious limitations for properly describing systems involving a multiconfigurational character. However, Zhao and Truhlar have proposed that the use of some functionals, such as the M06 functional, could allow attain a better description of these systems than the widely used B3LYP functional [18]. According to our results, for the ruthenium species investigated in this contribution there is agreement in the stability order predicted by the M06-DEF2-TZVP calculations and those obtained at MCSCF-MRMP2/DEF2 level, whereas important deviations were found for the relative energies calculated at the B3LYP-LANL2DZ level.

In our opinion, this can be addressed to the better performance of the M06 functional for describing the double bond type interaction between the ruthenium and the oxygen atom in the Ru^IVO(H₂O)₅²⁺ cation. However, it is important pointing out that the calculated energy value for the singlet electronic state of the penta-aquo oxo ruthenium complex using this exchange-correlation functional, is considerably higher (by roughly 30 kcal/mol) than the corresponding MCSCF-MRMP2/DEF2 value.

 

Conclusions

Results evolving from three levels of calculation, the MCSCF-MRMP2 approach and two DFT schemes, B3LYP-LANL2DZ and M06-DEF2-TZVP, have been used to calculate the geometrical parameters and the relative stability of some ruthenium compounds, mainly the Ru^IIIOH(H2O)5²⁺ and Ru^IVO(H2O)5²⁺ ions, which could be relevant in determining the preference of the reaction Ru(H₂O)₆²⁺ + H₂O₂ to yield radical species or high-valence oxo intermediates. Main differences between the results obtained through the different approaches used for describing the hydroxo and oxo ruthenium ions could arise from the multi-configurational character exhibited by the Ru^IVO(H₂O)₅²⁺ ion.

 

Computational details

For ruthenium, the Averaged Relativistic Effective Potential (AREP) and the triple-ζ quality Gaussian basis set (for the outer d and s shells) optimized for the corresponding atoms by LaJohn et al. were used [25]. A set of f-type polarization functions with exponent 1.235 was added to the basis set. The energy difference between the ⁵D ground state of Ru²⁺ and the first excited state ⁷S calculated by us using this basis and AREP is only 2.2 kcal/mol below the experimental difference (77.6 kcal/mol) obtained from the Moore's tables [26]. The oxygen atoms were described through the AREP and the triple-ζ basis for the 2s and 2p region provided by Pacios et al. [27, 28]. This basis set was augmented with a set of six-Cartesian d polarization functions with exponents 1.292. For the hydrogen atoms the standard 6-31++G** basis set was used [29-31].

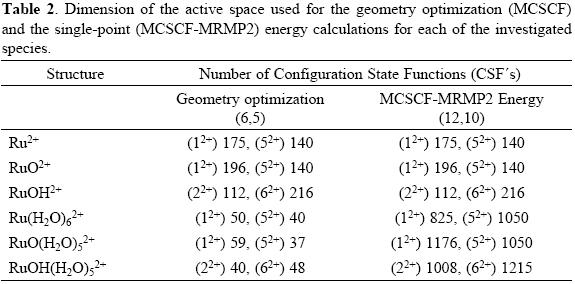
MCSCF geometry optimization calculations were performed for the singlet and quintuplet electronic states of each of the proposed intermediates without any symmetry restrictions (C₁). For these calculations the six d electrons were distributed in the five d orbitals, thus having an active space (6, 5). Each of the structures was characterized at the same level of calculation through normal-mode analysis. In order to improve the calculated values for the energy, single point calculations were carried out al MCSCF-MRMP2 level using an active space (12, 10) which included, besides the orbitals forming the active space (6, 5) used for geometry optimization calculations, the three orbitals lying below the d-shell and the two lowest lying unoccupied orbitals. For MRMP2 calculations the MCSCF active orbitals were used as the active space. In the Table 2 are collected the number of CSF's used for describing the electronic states of each of the different ruthenium species.

All these calculations were performed using the GAMESS quantum chemistry code [32].

Geometry optimization calculations for the electronic singlet state of the fragments involving the different aquo-com-plexes were also carried out using two DFT approaches, mainly the B3LYP and the M06 functionals. Calculations using the first functional (denoted as B3LYP-LANL2DZ throughout all the paper) were performed using the 6-31G* basis set for all light elements and the LANL2DZ basis set for ruthenium [33]. For the second level of theory, the M06 functional developed by Truhlar [34] combined with the DEF2- TZVP basis set [35] was used for describing all the atoms. The basis sets used for ruthenium in both type of DFT calculations implies the usage of effective core potentials to replace the 28-electron inner core [33, 36].

The geometry of each of the investigated cations was optimized at each of these levels of theory without symmetry restrictions. All the optimized structures were characterized as energy minima through normal-mode analysis. All the DFT calculations were carried out using Gaussian 09 package [37].

The analysis of the relative stability of the different ruthenium cations was made taken into account the stoichiometric relationship as determined by the reactants Ru(H₂O)₆²⁺ + H₂O₂ (or Ru²⁺ + H₂O₂).

 

Acknowledgements

This research was supported by the Universidad Nacional Autónoma de México (DGAPA-IN114512-2) and El Consejo Nacional de Ciencia y Tecnología (CONACYT-52309). A.E. Torres gratefully thanks to CONACYT for graduate scholarship (364788-245467).

 

References

1. Kirillova, M.V.; Kuznetsov, M.L.; Romakh, V.B. ; Shul'pina, L.S.; da Silva, J.J.R.F.; Pombeiro, A.J.L.; Shul'pin, G.B. J. Catal. 2009, 267, 140.         [ Links ]

2. Abbo, H.S.; Titinchi, S.J. J. Catal. 2010, 53, 254.         [ Links ]

3. Fenton, H.J.H. J. Chem. Soc. 1894, 65, 899.         [ Links ]

4. Neyens, E.; J. Baeyens, J. Journal of Hazardous Materials 2003, B98 33.         [ Links ]

5. Pestovsky, O.; Stoian, S. Bominaar, E.L.; Shan, X.; Münck, E.; Que, L. Jr.; Bakac, A. Angew. Chem. Int. Ed. 2005, 44, 6871.         [ Links ]

6. Bautz, J.; Bukowski, M.R.; Kerscher, M.; Stubna, A.; Comba, P.; Lienke, A.; Münck, E.; Que, L. Jr. Angew. Chem. Int. Ed. 2006, 45, 5681.         [ Links ]

7. Buda, F.; Ensing, B.; Gribnau, M.C.M.; Baerends, E. J. Chem. Eur. J. 2001, 7, 2775.         [ Links ]

8. Ensing, B.; Buda, F.; Blöchl, P.E.; Baerends, E.J. Phys. Chem. Chem. Phys. 2002, 4, 3619.         [ Links ]

9. Rachmilovich-Calis, S.; Masarwa, A.; Meyerstein, N.; Meyerstein, D.; Van Eldik, R.; Chem. Eur. J. 2009, 15, 8303.         [ Links ]

10. Kremer, M.L. J. Phys. Chem. A 2003, 107, 1734-1741.         [ Links ]

11. Wienhöfer, G.; Schröder, K.; Möller, K.; Junge, K.; Bellera, M. Adv. Synth. Catal. 2010, 352, 1615.         [ Links ]

12. Robbins, M.H.; Drago, R.S. J. Chem. Soc., Dalton Trans. 1996, 105.         [ Links ]

13. Goidstein, A.S.; Beer, R.H.; Drago, R.S. J. Am. Chem. Soc. 1994, 116, 2424.         [ Links ]

14. Tse, M.K.; Bhor, S.; Klawonn, M.; Anilkumar, G.; Jiao, H.; Spannenberg, A.; Döbler, C.; Mägerlein, W.; Hugl, H.; Beller, M. Chem. Eur. J. 2006, 12, 1875.         [ Links ]

15. Shi, F.; Tse, M.K.; Beller, M. Journal of Molecular Catalysis A: Chemical 2007, 270, 68.         [ Links ]

16. Chatterjee, D.; Mitra, A.; Van Eldik, R. Dalton Trans. 2007, 943.         [ Links ]

17. Kulkarni, A.D.; Truhlar, D.G. J. Chem. Theory Comput. 2011, 7, 2325.         [ Links ]

18. Zhao, Y.; Truhlar, D.G. Acc. Chem. Res. 2008, 41, 157.         [ Links ]

19. Jaque, P.; Marenich, A.; Cramer, C.; Truhlar, D. J., Phys. Chem. C, 2007, 111, 5783-5799.         [ Links ]

20. Bernhard, P.; Bürgi, H.-B.; Hauser, J.; Lehmann, H.; Ludi, A. Inorg. Chem. 1982, 21, 3936.         [ Links ]

21. Bernhard, P.; Ludi, A. Inorg. Chem. 1984, 23, 870.         [ Links ]

22. Brunschwig, B.S.; Creutz, C.; Macartney, D.H.; Sham, T.-K.; Sutin, N. Faraday Discuss. Chem. Soc., 1982, 74, 113.         [ Links ]

23. Åkesson, R.; Pettersson, L.G.M.; Sandström, M.; Wahlgren, U. J. Am. Chem. Soc. 1994, 116, 8691.         [ Links ]

24. Kojima, T.; Nakayama, K.; Ikemura, K.; Ogura, T.; Fukuzumi, S. J. Am. Chem. Soc. 2011, 133, 11692.         [ Links ]

25. LaJohn, L.A.; Christiansen, P.A.; Ross, R. B.; Atashroo, T.; Ermler, W.C. J. Chem. Phys., 1987, 87, 2812.         [ Links ]

26. Moore, C.E. Table of Atomic Energy Levels (National Bureau of Standards, 35/V Circular 467, Washington, D.C., 1971).         [ Links ]

27. Pacios, L. F.; Gómez, P. C. Int. J. Quantum Chem. 1994, 49, 817.         [ Links ]

28. Pacios, L. F.; Christiansen, P. A. J. Chem. Phys. 1985, 82, 2664.         [ Links ]

29. Hehre, W. J.; Ditchfield, R.; Pople, J. A. J. Chem. Phys. 1972, 56, 2257.         [ Links ]

30. Hariharan, P. C.; Pople, J. A. Theoret. Chimica Acta 1973, 28, 213.         [ Links ]

31. Clark, T.; Chandrasekhar, J.; Schleyer, P. V. R. J. Comp. Chem. 1983, 4, 294.         [ Links ]

32. Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.; Gordon, M. S.; Jensen, J. H.; Koseki, S.; Matsunaga, N.; Nguyen, K. A.; Su, S. J.; Windus, T. L.; Dupuis, M.; Montgomery, J. A. J. Comput. Chem. 1993, 14, 1347.         [ Links ]

33. Hay, P. J.; Wadt, W. R. J. Chem.Phys. 1985, 82, 299.         [ Links ]

34. Zhao, Y.; Truhlar, D.G. Theor. Chem. Acc. 2008, 120, 215.         [ Links ]

35. Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297.         [ Links ]

36. Andrae, D.; H€aussermann, U.; Dolg, M.; Stoll, H.; Preuss, H. Theor. Chem. Acc. 1990, 77, 123.         [ Links ]

37. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J. A., Jr.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, N. J.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, €O.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, 2009.         [ Links ]

 

Note

* The asterisk indicates the name of the author to whom inquires about the paper should be addressed.