Artículo

 

Noble Gases Encaged by the C₆₀ Increase Their Chemical Reactivity

 

Avelino Cortés-Santiago,^1,2 Rubicelia Vargas¹ and Jorge Garza^2,*

 

¹ Departamento de Química, División de Ciencias Básicas e Ingeniería. Universidad Autónoma Metropolitana-Iztapalapa. San Rafael Atlixco 186, Col. Vicentina. Iztapalapa. C. P. 09340. México D. F. México.

² Benemérita Universidad Autónoma de Puebla. Facultad de Ciencias Químicas. Av. San Claudio y 18 Sur. Puebla, Puebla, C.P. 72530. jgo@xanum.uam.mx

 

Received December 06, 2011.
Accepted March 26, 2012.

 

Abstract

In this work, we use a spherical shell with an attractive potential to simulate the C₆₀ and its effects on, He, Ne, Ar and Kr when each atom is in the center of the sphere. Within the Kohn-Sham model, two exchange-correlation functionals were used; the main difference between these two functionals is that one incorporates explicitly the self-interaction correction and the correct asymptotic behavior of the exchange-correlation potential, and the other one does not contain such corrections. We found that the considered atoms are softer inside of the cage than when they are free. By using several chemical reactivity predictors as the electrodonating and electroaccepting powers, defined by Professor Gázquez et al. (J. Phys. Chem. A 2007, 111, 1966), it is proved that the noble gases increase their chemical reactivity when they are immersed in the C₆₀. Naturally, this conjecture must be confirmed by more realistic models, but at first glance this is a very interesting conclusion and opens a new possibility to obtain reactions with encaged inert gases.

Keywords: Fullerene, Confined Atoms, DFT Chemical Predictors, Hardness and Softness.

 

Resumen

En este trabajo, usamos un cascarón esférico con un potencial atractivo para simular al C₆₀ y sus efectos sobre el He, Ne, Ar y Kr cuando cada átomo está en el centro de la esfera. Dentro del modelo de Kohn-Sham, dos funcionales de intercambio y correlación fueron usados; la principal diferencia entre estos dos funcionales es que uno incorpora explícitamente la corrección a la autointeracción y el comportamiento asintótico correcto, y el otro no contiene tales correcciones. Encontramos que los átomos considerados son más blandos dentro de la caja que cuando están libres. Usando varios predictores de reactividad química, como las potencias electrodonadoras y electroaceptoras, definidas por el profesor Gázquez y colaboradores (J. Phys. Chem. A 2007, 111, 1966), se prueba que los gases nobles incrementan sus reactividad química cuando están inmersos en el C60. Naturalmente, esta conjetura debe de ser confirmada por modelos más realistas, pero a primera vista esta es una conclusión muy interesante y abre una nueva posibilidad de obtener reacciones con gases inertes encajonados.

Palabras claves: Fulereno, átomos confinados, predictores químicos de la TFD, dureza y blandura.

 

Introduction

Recently, the study of confined systems has received attention of experimental and theoretical groups. Without doubt, the confinement exerted on quantum systems has given unexpected trends on chemical and physical properties of the matter. The confinement imposed by fullerenes or nanotubes is a hot topic nowadays since it opens possible technological applications [1-10]. One way to study the electronic structure of systems encaged by fullerenes is by solving the Kohn-Sham [11] or Hartree-Fock [12] equations for the whole system; the fullerene (host) plus the corresponding enclosed guest. Naturally, this strategy is used to study the fullerene effects on quantum systems enclosed by these cages. However, sometimes one is interested only on the electronic structure of the guest when it is confined, and the host-guest model does not provide this information because the host electrons are also presented. Thus, several confinement models have been used to study the guest response when it is enclosed by a confinement [13]. Recently, a model for the C₆₀ has been reported in order to see the effects exerted by this system on the hydrogen atom giving interesting results [14]. A natural extension of that model is its application on many-electron atoms. Accordingly, we present in this study a detailed discussion on the chemical reactivity predictors of noble gases enclosed by the C₆₀ model.

 

Theoretical framework

Modeling the C₆₀

From the study performed by Xu et al. for the C₆₀ modeling [15], there are many reports where the cage imposed by the fullerene has been useful to describe the effects on confined atomic systems [13, 16-23]. Such a model is based mainly on the following two assumptions: 1) The fullerene can be modeled by a spherical shell. 2) The spherical shell represents an attractive potential suggested by the experimental photoelectron spectroscopy. The first proposal to the C60 model is based on a step potential, U_S, which expression is [17]

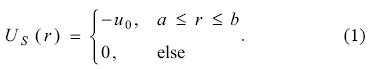
In equation (1), u₀, a and b represent a constant potential, the radius of the inner sphere and the radius of the external sphere of the shell, respectively. With this simple model it is possible to gain insight about the effects induced by the C₆₀ on atomic systems, many of them are related with optical properties. Recently, Nascimento et al. [14] have published an alternative potential to simulate the C₆₀, in this model the step potential is substituted by a gaussian function with the following mathematical expression

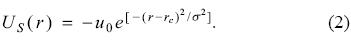
In this equation r_c represents the position where the gaussian function is centered, σ its width and u₀ has the same meaning than in equation (1). Evidently, the application of this model on many-electrons atoms is a natural step. The main concern of this work is related to the chemical reactivity of atoms, noble gases in particular, when these systems are within the shell defined by equation (2).

 

Chemical reactivity predictors

The concepts provided by the density functional theory have been used to rationalize the initial stages of chemical reactions [24-26]. Many of them are based on derivatives with respect to the number of electrons, as the electronegativity, χ, which is obtained from the chemical potential, μ, trough the equation [27]

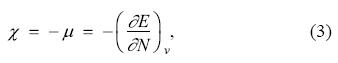
or the hardness, η [28],

In these equations the total energy is represented by E, the number of electrons by N and the external potential by υ. From these predictors, the electrophilicity, ω, is obtained by the expression [29]

By the nature of the electronic structure in atoms and molecules it is important the directionality on the derivatives evaluation with respect to the number of electrons [30]. Thus, the chemical potential must be evaluated as

where ± indicates if the system will gain (+) or lose (-) electrons. For neutral systems the hardness adopts the form [31]

By applying the directionality concept, the professor Gázquez and coworkers defined the electrodonating and electroaccepting powers as [32]

These definitions are important to elucidate the chemical behavior on systems involved in charge transfer processes. It is worth noting that the hardness used by the professor Gázquez was obtained by assuming that η = η⁺ = η^- with η given by equation (7), which is the same position assumed in this work. Evidently, we are just mentioning the necessary elements for our discussion; if the reader wants to know more details about the chemical predictors provided by the DFT, the reference [33] is quite recommendable due to it was published recently in this journal by the professor Gázquez.

 

Computational details

According to equation (8) to evaluate ω⁺ and ω^-, we can follow the following steps: a) Compute the energy derivatives with respect to the number of electrons, taking into account the directionality in order to obtain μ⁺ and μ^-. b) Compute the hardness for the neutral systems according to equation (7). c) Compute the electroaccepting and electrodonating powers by using equation (8). For this study we have used fractional occupancy, it means, we have computed the total energy for the neutral system and 8 additional points, four to the right and four to the left with increments of 0.01 electrons. By using the Lagrange interpolating polynomial we estimated the derivative from the right side (+) with five points, and the same procedure was applied for the left side (-), all derivatives were evaluated on the neutral system. Thus, in this work we have performed 9 calculations for each atom. These steps were applied on He, Ne, Ar and Kr atoms when they are confined by the C₆₀ and when they are free. The exchange contribution was that reported by Dirac (D) [34] and the correlation contribution was that reported by Perdew and Wang (PW92) [35]. It is well known that many exchange-correlation functionals do not cancel correctly the self-interaction energy[36], thus we applied a self-interaction correction (SIC) proposed by Perdew and Zunger [37]. Additionally, since the shell is not close to the nucleus it is important to apply a correction to the asymptotic behavior by using the optimized effective potential (OEP) [38, 39] in the context of the Krieger-Lee-Iafrate approximation [40, 41]. Details about this implementation can be found in references [42-44]. Thus, we report the results obtained with the DPW92 exchange-correlation functional and its correction DPW92-SIC-OEP, in this way we have performed 144 calculations for the four considered atoms with a modified version of the Herman-Skillman numerical code[45], thus the basis set functions effects are not present.

 

Results and discussion

We are reporting in Table 1 the total energies obtained for the noble gases, free and encaged, by using the DPW92 and DPW92-SIC-OEP exchange-correlation functionals, for several charge values. With this table we want to stress the difference between the total energy obtained when the SIC-OEP is applied or when the atom is confined by the fullerene, or by both effects. Clearly, the SIC-OEP approximation gives lower total energies than when this approximation is not applied, which has been discussed elsewhere [42, 44]. Thus, our discussion will be centered on the DPW92-SIC-OEP exchange-correlation functional since it gives the lowest energies and it was designed to obtain the correct asymptotic behavior on the corresponding potential. The first important trend observed from Table 1 is related with the small changes obtained on the total energy when the noble gases are free and they try to bind additional electrons. This trend is connected with the small electronegativity values observed on these systems. However, this trend is reverted when the atoms are confined by the shell of attractive potential, which represents the fullerene.

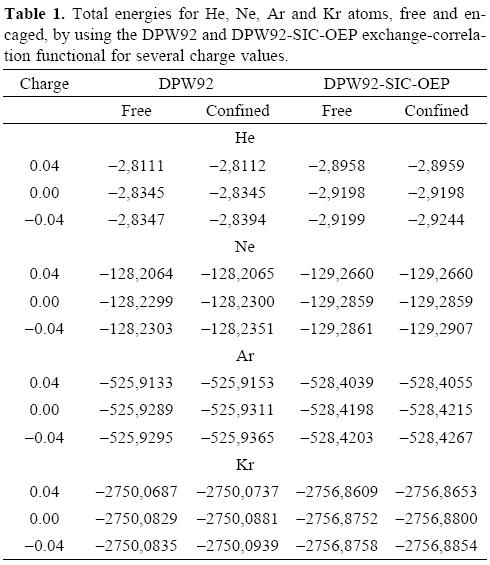
In order to see the total energy changes as a function of the number of electrons, in Figure 1 these changes are plotted for the four atoms considered in this work. In these plots we used the neutral atom as a reference, for this reason the energy of this system is zero. One important characteristic observed in all plots is the straight line obtained when the number of electrons is changed, which corresponds to the expected behavior for atoms where a new shell is opening and when the correct asymptotic behavior of the exchange-correlation potential is applied, as that associated to the DPW92-SIC-OEP approach. By analyzing these plots we can conclude that the slope related with the electron accepting process is increased when the noble gases are confined by the fullerene. Contrary to this behavior, the free or confined atom gives a similar behavior to each other when the atom tries to give electrons. Consequently, the chemical potentials μ⁺ will change since it represents the slope of the straight line when the considered atoms accept electrons. In Table 2 we are reporting the chemical potentials for the four atoms, when they are confined or free, and for the two exchange-correlation approximations. The value obtained for μ⁺ is the first important result obtained when numerical derivatives are computed on free noble gases atoms since this quantity is close to zero, which corresponds to the expected behavior for these systems. Then, according to our procedure, the μ⁺ predicts that the free noble gases will not accept additional electrons. This behavior is clearly changed when these atoms are inside of the C₆₀ because all of them increase in an important way this quantity. In conclusion, noble gases increase their chemical potential, to bind electrons, when they are encaged by the C₆₀. It is important to note the positive values predicted by the DPW92 exchange-correlation functional for He and Kr. This incorrect result could be a consequence of the numerical derivative or by an intrinsic problem of the exchange-correlation functional, we think this last possibility is the responsible of such a behavior since it is corrected by the SIC-OEP approximation.

It is interesting the behavior observed for μ^-, with regard to μ⁺, since whereas μ⁺ goes up μ^- goes down, in absolute value, for the encaged atom. Such a result is observed just when the SIC-OEP approach is applied. In fact, μ^- is almost the same for the free or the confined atom when this correction is used. Thus, the potential imposed by the gaussian function acts just for atoms accepting additional electrons.

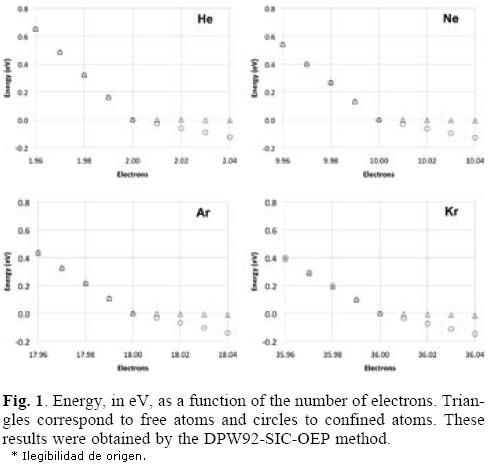
In the same table we are reporting in parenthesis the hardness, and it is observed another interesting trend; the hardness for noble gases is reduced with regard to the free system, in other words, the noble gases are softer within the fullerene than when they are free. Naturally, this result must be connected with the changes produced in the electron density. In Figure 2, we are presenting the difference between the orbital densities obtained for free and enclosed atoms, ρ^confined-ρ^free. In particular, we are reporting the behavior exhibited by some of the orbital densities for the Kr atom. Clearly, the most affected orbitals are those belonging to the valence shell in a region close to the gaussian potential. Furthermore, in this region ρ^confmed > ρ^free, suggesting that the polarizability will be increased, which must be confirmed in a future work.

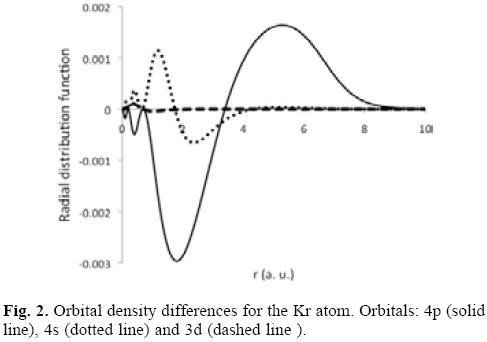
Finally, electrodonating and electroaccepting powers are reported in Table 3. Clearly, the electroaccepting power is zero when these atoms are free, however when these atoms are encaged by the fullerene their response is completely different, even for the confined He atom this quantity is not zero. Naturally, the Kr atom is the system that presents the biggest response. At this point one question arises: are the values found for the chemical predictors, big or small? We have evaluated the same chemical reactivity predictors in the free Mg atom, with the DPW92-SIC-OEP method. For this system we found that μ⁺ = -0.050, μ^- = -0.175, η = 0.126 , ω⁺ = 0.010 and ω^- = 0.122, (all of them in atomic units). Comparing these numbers with those reported in Tables 2 and 3, clearly Ne, Ar and Kr encaged by the C₆₀ show a bigger electrodonating power than the free Mg atom. From here, we are confident of say that the noble gases increase their chemical reactivity when they are encaged by the C₆₀. We used as reference the Mg atom, such a decision is totally arbitrary although this atom sometimes is considered to be studied inside of fullerenes. Naturally, it is necessary for a study of the whole periodic table under a confinement similar to that considered in this work. Evidently, we are currently performing such a study in our laboratory.

 

Conclusions

By using a simple model for the C₆₀, some global chemical reactivity predictors as the chemical potentials, hardness, electrodonating and electroaccepting powers were evaluated for He, Ne, Ar and Kr atoms. As important results found in this study, we can mention the reduction on the hardness, the increasing on μ⁺ and on ω⁺ when these atoms are confined by the fullerene compared with the free atoms. These results suggest an increment on the chemical reactivity of these systems; evidently, this prediction must be confirmed by more realistic models, where even the van der Waals interactions could be incorporated [46]. Currently, this topic is being developed in our group.

 

Acknowledgments

We thank the Laboratorio de Supercómputo y Visualización en Paralelo at the Universidad Autónoma Metropolitana-Iztapalapa for the access to its computer facilities. Financial support for A. C.-S. was partially provide by PROMEP, México. J. G. and R. V. thank CONACYT, México, for the financial support through the projects 155070 and 154784 respectively.

 

References

1. Bethune, D. S.; Johnson, R. D.; Salem, J. R.; Devries, M. S.; Yannoni, C. S. Nature 1993, 366, 123-128.         [ Links ]

2. Dillon, A. C.; Jones, K. M.; Bekkedahl, T. A.; Kiang, C. H.; Bethune, D. S.; Heben, M. J. Nature 1997, 386, 377-379.         [ Links ]

3. Estrada-Salas, R. E.; Valladares, A. A. J. Mol. Struct. Theochem 2008, 869, 1-5.         [ Links ]

4. Li, G.; Sabirianov, R. F.; Lu, J.; Zeng, X. C.; Mei, W. N. J. Chem. Phys. 2008, 128, 074304-074304(6).         [ Links ]

5. Sano, N.; Suzuki, T.; Hirano, K.; Akita, Y.; Tamon, H. Plasma Sources Sci. & Tech. 2011, 20, 034002-034002(8).         [ Links ]

6. Tellgmann, R.; Krawez, N.; Lin, S. H.; Hertel, I. V.; Campbell, E. E. B. Nature 1996, 382, 407-408.         [ Links ]

7. Wan, H. J.; Zhao, F. Q.; Zeng, B. Z. Coll. Surf. B-Biointerfaces 2011, 86, 247-250.         [ Links ]

8. Yang, S. Y.; Yoon, M.; Hicke, C.; Zhang, Z. Y.; Wang, E. Phys. Rev. B 2008, 78, 115435-115435(5).         [ Links ]

9. Zhang, M.; Harding, L. B.; Gray, S. K.; Rice, S. A. J. Phys. Chem. A 2008, 112, 5478-5485.         [ Links ]

10. Madjet, M. E.; Chakraborty, H. S.; Manson, S. T. Phys. Rev. Lett. 2007, 99, 243003-243003(4).         [ Links ]

11. Kohn, W.; Sham, L. J. Phys. Rev. 1965, 140, 1133-1138.         [ Links ]

12. Slater, J. C. The Calculation of Molecular Orbitals; John Wiley and Sons: New York, 1979.         [ Links ]

13. Dolmatov, V. K.; Baltenkov, A. S.; Connerade, J. P.; Manson, S. T. Rad. Phys. Chem. 2004, 70, 417-433.         [ Links ]

14. Nascimento, E. M.; Prudente, F. V.; Guimaraes, M. N.; Maniero, A. M. J. Phys. B 2011, 44, 015003 (7pp).         [ Links ]

15. Xu, Y. B.; Tan, M. Q.; Becker, U. Phys. Rev. Lett. 1996, 76, 35383541.         [ Links ]

16. Connerade, J. P.; Dolmatov, V. K.; Lakshmi, P. A. J. Phys. B 2000, 33, 251-264.         [ Links ]

17. Connerade, J. P.; Dolmatov, V. K.; Lakshmi, P. A.; Manson, S. T. J. Phys. B 1999, 32, L239-L245.         [ Links ]

18. Connerade, J. P.; Dolmatov, V. K.; Manson, S. T. J. Phys. B 1999, 32, L395-L403.         [ Links ]

19. Connerade, J. P.; Dolmatov, V. K.; Manson, S. T. J. Phys. B 2000, 33, 2279-2285.         [ Links ]

20. Dolmatov, V. K.; Brewer, P.; Manson, S. T. Phys. Rev. A 2008, 78, 013416-013416(7).         [ Links ]

21. Dolmatov, V. K.; Connerade, J. P.; Lakshmi, A. P.; Manson, S. T. Surf. Rev. Lett. 2002, 9, 39-43.         [ Links ]

22. Dolmatov, V. K.; Manson, S. T. J. Phys. B 2008, 41, 165001-165001(4).         [ Links ]

23. Baltenkov, A. S.; Becker, U.; Manson, S. T.; Msezane, A. Z. J. Phys. B 2010, 43, 115102-115102(9).         [ Links ]

24. Chattaraj, P. K.; Sarkar, U.; Roy, D. R. Chem. Rev. 2006, 106, 2065-2091.         [ Links ]

25. Chermette, H. J. Comput. Chem. 1999, 20, 129-154.         [ Links ]

26. Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103, 1793-1873.         [ Links ]

27. Parr, R. G.; Donnelly, R. A.; Levy, M.; Palke, W. E. J. Chem. Phys. 1978, 68, 3801-3807.         [ Links ]

28. Parr, R. G.; Pearson, R. G. J. Am. Chem. Soc. 1983, 105, 7512-7516.         [ Links ]

29. Parr, R. G.; Von Szentpaly, L.; Liu, S. B. J. Am. Chem. Soc. 1999, 121, 1922-1924.         [ Links ]

30. Ayers, P. W. J. Mathem. Chem. 2008, 43, 285-303.         [ Links ]

31. Ayers, P. W.; Parr, R. G. J. Am. Chem. Soc. 2000, 122, 2010-2018.         [ Links ]

32. Gázquez, J. L.; Cedillo, A.; Vela, A. J. Phys. Chem. A 2007, 111, 1966-1970.         [ Links ]

33. Gázquez, J. L. J. Mex. Chem. Soc. 2008, 52, 3-10.         [ Links ]

34. Dirac, P. A. M. Proc. Cambridge Phil. Soc. 1930, 26, 376-385.         [ Links ]

35. Perdew, J. P.; Wang, Y. Phys. Rev. B 1992, 45, 13244-13249.         [ Links ]

36. Kummel, S.; Kronik, L. Rev. Mod. Phys. 2008, 80, 3-60.         [ Links ]

37. Perdew, J. P.; Zunger, A. Phys. Rev. B 1981, 23, 5048-5079.         [ Links ]

38. Sharp, R. T.; Horton, G. K. Phys. Rev. 1953, 90, 317-317.         [ Links ]

39. Talman, J. D.; Shadwick, W. F. Phys. Rev. A 1976, 14, 36-40.         [ Links ]

40. Krieger, J. B.; Li, Y.; Iafrate, G. J. Phys. Rev. A 1992, 46, 5453-5458.         [ Links ]

41. Krieger, J. B.; Yan, L.; Iafrate, G. J. Phys. Rev. A 1992, 45, 101126.         [ Links ]

42. Garza, J.; Nichols, J. A.; Dixon, D. A. J. Chem. Phys. 2000, 112, 7880-7890.         [ Links ]

43. Garza, J.; Nichols, J. A.; Dixon, D. A. J. Chem. Phys. 2000, 112, 1150-1157.         [ Links ]

44. Garza, J.; Vargas, R.; Nichols, J. A.; Dixon, D. A. J. Chem. Phys. 2001, 114, 639-651.         [ Links ]

45. Herman, F.; Skillman, S. Atomic Structure Calculations; Prentice-Hall: New-Jersey, 1963.         [ Links ]

46. Tkatchenko, A.; Scheffler, M. Phys. Rev. Lett. 2009, 102, 073005-073005(4).         [ Links ]

 

Note

* The asterisk indicates the name of the author to whom inquires about the paper should be addressed.