Article

 

Drug Design Outlook by Calculation of Second Virial Coefficient as a Nano Study

 

M. Monajjemi,¹'* F. Naderi,² F. Mollaamin,³ and M. Khaleghian⁴

 

¹ Department of Chemistry, Science and Research Branch, Islamic Azad University, Tehran, Iran.

² Department of Chemistry, Shahr–e Qods Branch, Islamic Azad University, Tehran, Iran.

³ Department of Chemistry, Qom Branch, Islamic Azad University, Qom, Iran.

⁴ Department of Chemistry, Eslamshahr Branch, Islamic Azad University, Tehran, Iran. * m_monajjemi@yahoo.com

 

Received December 19, 2011.
Accepted March 1, 2012.

 

Abstract

Intermolecular potential energy surface for an interaction of drug with Na has been examined using HF level of theory with 6–31G* basis set. The name of drug is meso–tetrakis (p–sulphonatophenyl) porphyrin (here after abbreviated to TSPP) . The numbers of Na⁺ have a significant effect on the calculated potential energy curve (including position, depth, and width of the potential well). Counterpoise (CP) correction has been used to show the extent of the basis set superposition error (BSSE) on the potential energy curves obtained for TSPP–Na. The second virial coefficients are calculated by these data.

Key words: Drug, virial coefficient, potential energy surface.

 

Resumen

Se examina la superficie de energía potencial intermolecular para una interacción de un fármaco con Na usando el nivel de teoría HF con el conjunto de base 6–31G*. El nombre del fármaco es meso–tetrakis (p–fenilsulfonato) porfirina (subsecuentemente abreviado como TSPP). El número de Na⁺ tiene un efecto significativo en la curva de energía potencial calculada (incluyendo posición, profundidad, y ancho del pozo de potencial). Se utilizó la corrección de counterpoise (CP) para mostrar el tamaño del error de superposición de base (BSSE) en las curvas de energía potencial obtenidas para el TSPP–Na. Los segundos coeficientes viriales se calcularon a partir de estos datos.

Palabras clave: Fármaco, coeficiente virial, superficie de energía potencial.

 

Introduction

A way to obtain an intermolecular potential is made available by quantum chemistry. Using quantum chemical methods, detailed information about the interaction energy over a wide area of the potential surface can be derived.

A number of package codes, such as MOLPRO [1], COLUMBUS [2–4] are available. Unfortunately, these powerful tools do not currently solve all of the problems [5].

However, apart from the simplest systems, one has to use some level of approximation in quantum chemical calculations.

In quantum chemistry, the computation of the energy and wavefunction of an average–size molecule is a formidable task that is alleviated by the Born–Oppenheimer (BO) approximation, named after Max Born and J. Robert Oppenheimer. For instance the benzene molecule consists of 12 nuclei and 42 electrons. The time independent Schrödinger equation, which must be solved to obtain the energy and molecular wavefunc–tion of this molecule, is a partial differential eigenvalue equation in 162 variables —the spatial coordinates of the electrons and the nuclei. The BO approximation makes it possible to compute the wavefunction in two less complicated consecutive steps. This approximation was proposed in 1927, in the early period of quantum mechanics, by Born and Oppenheimer and is still indispensable in quantum chemistry.

Potential energy surfaces may be determined by ab initio electronic structure calculations. If one makes the Born–Oppenheimer approximation, the molecular wave function is written as:

Where Ψ_e is the electronic wave function, which depends on the electron coordinates r and nuclear coordinates R, and Ψ_n is the nuclear wave function.

With the Born–Oppenheimer separation, each electronic state of the chemical reactive system has a potential energy surface. Knowledge of the ion–ion interaction potential is a key ingredient in the analysis of nuclear reactions. By using the potential between nuclei, we can estimate the cross sections of different nuclear reactions. The ion–ion interaction potential related to the Coulomb repulsion force and the nuclear attraction force has, as a rule, the barrier and the capture potential well near a touching point. The Coulomb part of the ion–ion potential is well–known. In contrast, the nuclear part of the nucleus–nucleus potential is less defined.

This paper reports a study on interaction of TSPP (Scheme 1) with one, two, three and four Na⁺ respectively. Porphyrines represent an interesting family of compounds used now for the photodynamic therapy (PDT) of malignant tumors [6]. Porphyrines have attracted large attention because of their role in the human body, ability to accumulate in many kinds of cancer cells, as well as magnetic and optical properties. These features make them useful in cancer medicine and photody–namic therapy [7]. Porphyrins and metalloporphyrins provide a relatively unexplored class of compounds because of their large size, ease of synthesis, bioactivity, excellent thermal stability and the diversity of their coordination and catalytic chemistry. Furthermore, porphyrins provide an extremely versatile platform on which to build desired peripheral functionality with designed orientations. Functionalization of the porphyrin macro cycle has always received much attention, and considerable progress has been made over the past decades [8–11].

Theoretical back ground and computational method

Initially, structure of TSPP was fully optimized with the HF method and 6–31G* basis set in order to locate the stationary points on the potential surface. Our calculations were performed by using the program package Gaussian 98 [2].The interaction energy for each minimum was calculated by using the supermolecule method.

In ab initio calculations the basis set superposition error (BSSE) is of paramount importance. This error can be eliminated to some extent by using the counterpoise method (CP). In this method both the physicochemical compound A – B and the A and B components at r = ∞ are calculated by using the full basis set for the A – B, hence

Where

This study has been carried out just in vacuum because of limitation in software and computers which we have. We tried to make constant the angle and position between the average plan of TSPP and the vector TSPP–Na for 4 sides which Na approached.

Ab initio calculation of the interaction energy in the system

Using quantum chemical methods, detailed information about the interaction energy over a wide area of the potential surface can be derived. This approach can be used to extract detailed information of the potential energy surface, which is sometimes difficult or practically impossible by other methods. The basis set superposition error has a significant effect on the calculated interaction potential and therefore it should be corrected for [13].

The significant of the BSSE on the intermolecular interaction has been highlighted in a number of papers. The various points on the ab initio potential energy surface were used to obtain a fit to the Lennard–Jones and Morse and Morse modified potential energy function.

Virial Coefficients

The second virial coefficient as a pure two body interaction property has been calculated to give a first simple test of the quality of intermolecular interaction potential.

Assuming the known form for U(r), the hard sphere approximation leads to the following expression for the estimation of second virial coefficient [14, 15]:

where N_A is Avogadros number, k is the Boltzmann constant, T is the temperature. It was though for many years that the values for the second virial coefficient do not depend on the shape of the curve U(r) for the energy interaction but only on the integral that correspond to the area restricted by this curve.

 

Results and Discussion

We calculated the intermolecular interaction energies of the TSPP with one, two, three and four Na⁺ respectively.

The intermolecular potential energy interaction obtained at HF level of theory with the basis set 6–31G* that plotted in figure 1 as function of R; the distance between TSPP and Na. Calculated potential energy curves, including position, depth and width of potential well were shown in Fig. 1. The calculated potential energy surface can be compared based on the values of the position of the minimum point (r_e) of the potential curves. As is evident from this table, these quantities are very sensitive to the number of metal used in the computations. In ab initio calculations the basis set superposition error is of paramount importance. BSSE corrected TSPP–Na intermolecular potential energy curves corresponding to those calculated, are plotted against r in figure 1. In this figure the values of U (calculated by Gaussian) and UM (calculated by Morse modified function are fitted by Excel) are shown.

Most of the popular approximation such as, for instance, the Lennard–Jones potential and the exp–6 potential and Kihara potential yielded unsatisfactory results. Finally, we have chosen the six–parameter generalized Morse modified function [16].

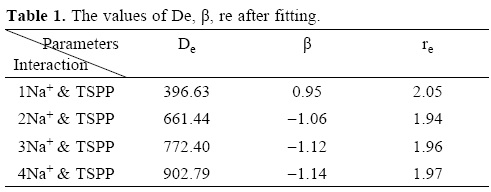
De, β Re are positive and usually chosen to fit the bond dissociation energy, the harmonic vobration frequency and the equilibrium bond length.

D_e,β_e,r_e and A, B, C parameters are fitted in the approximation procedure. The results of search are shown in Table 1.

The values of U (calculated by Gaussian program) and UM (calculated by Morse modified function) and r are shown in tables 2, 3, 4, 5.

The second virial coefficient as a pure two body interaction property has been calculated to give a first simple test of the quality of intermolecular interaction potential. The values of them are listed in tables 6, 7, 8, 9 and calculated results with using MATLAB and MAPLE software are plotted in figure 2.

 

Conclusion

After study of the interaction of drug with Na using Hartree–Fock method, it has been seen that the numbers of Na⁺ Cations have a important effect on the theoretical calculated potential energy curve. Also, Counterpoise (CP) correction has been calculated to investigate the extent of the basis set superposition error on the potential energy curves obtained for TSPP–Na and the second Virial coefficients are calculated by these data.

 

References

1. Werner, H. J.; Knowles, P. J.; Almof, J.; Amos, R. D.; Deegan, M. J. O.; Elbert, S. T.; Hample, C.; Meyer, W.; Peterson, K.; Pitzer, R.; Ston, A. J.; Taylor, P. R.; Lindh, R. University of Birmingham, Birmingham, 1996.         [ Links ]

2. Lischka, H.; Shepard, R.; Brown, F. B.; Shavitt, I. Int. J. Quantum Chem., Quantum Chem. Symp. 1981, 75, 91.         [ Links ]

3. Shepard, R.; Shavitt, I.; Pitzer, R. M.; Comeau, D. C.; Pepper, M.; Lischka, H.; Szalay, P. G.; Ahlrichs, R.; Brown, F. B.; Zhao, J. Int. J. Quantum Chem., Quantum Chem. Symp. 1988, 22, 149.         [ Links ]

4. Lischka, H.; Shepard, R.; Pitzer, R. M.; Shavitt, I.; Dallos, M.; Muller, T.; Szalay, P. G.; Seth, M.; Kedziora, G. S.; Yabushita, S.; Zhang, Z.; Phys. Chem. Chem. Phys. 2001, 3, 664.         [ Links ]

5. Naroznik, M.; J. Molecular Structure (Theochem), 2003, 624, 267–273.         [ Links ]

6. Lukyanets, E. A.; Russ, J. Chem. 1998, 42, 9–16.         [ Links ]

7. Gaiduk, M. I.; Grigryants, V. V.; Mirnov, A. F.; Rumyantsera, V. D.; Ghissov, V. I.; Sukhin, G. M. J. Photochem. Photobiol. B. Biol., 1990, 7, 15.         [ Links ]

8. Morgan B. and Dolphin D. (Eds.) Synthesis and Structure of Biomimetic Porphyrins, Springer Verlag: Berlin, 1987, 64, 115.         [ Links ]

9. Kim, R. M.; Fate, G. D.; Gonzales, J. E.; Lahiri, J.; Ungashe, S. B.; Groves, J. T. NATO ASI Ser., Ser. C. 1995, 459, 4956.         [ Links ]

10. Ogoshi, H.; Mizutani, T. Biomimetic Reactions Catalyzed by Metalloporphyrins; Murakami Y. (Ed.) Vol. 4, Elsevier: Oxford, U.K., 1996, 337–385.         [ Links ]

11. Kadish, K. M.; Smith, K. M.; Guilard, R. The Porphyrin Handbook (Eds.), Academic Press: San Diego, 2000–2003, 120.         [ Links ]

12. Frisch, M. J. et al. Gaussian 98, Revision A.9, Gaussian, Inc., Pittsburgh, PA, 1998.         [ Links ]

13. Boys, S. F.; Bernardi, F. Mol. Phys., 1970, 19, 553.         [ Links ]

14. Harold, C. "Molecular Schrödinger Equation. VIII. A New Method for the Evaluation of Multidimensional Integrals", Journal of Chemical Physics, 1967, 47, 5307.         [ Links ]

15. Kammerlingh Onnes, H. "Expression of the equation of state of gases and liquids by means of series", Communications from the Physical Laboratory of the University of Leiden 1901, 71, 3–25.         [ Links ]

16. Hase, W. L.; Mondro, S. L.; Duchovic, R. J.; Hirst, D. M. J. Am. Chem. Soc., 1987, 109, 2916.         [ Links ]