A la memoria de Manuel Márquez Cabrera (†), amigo cuya naturaleza fue
la honestidad y la rectitud. Te recordaremos siempre.
Introducción
En este ensayo entenderemos por “lógica” “a una ciencia formal que abarca tanto los problemas de formalización de los lenguajes naturales como de los métodos para determinar la validez de las inferencias” (Palau, 2014: 15). Es claro que esta definición marca una diferencia con la así llamada lógica natural o lógica folk.1 Ahora bien, la lógica, en tanto ciencia formal, trabaja con un lenguaje que podemos denominar “artificial” (distinto del lenguaje natural)2 que se expresa con una nomenclatura propia la cual facilita su comprensión y atención. Gracias al uso de los símbolos, la lógica puede “exhibir con mayor claridad las estructuras lógicas de argumentos cuya formulación puede quedar oscura en el lenguaje ordinario” (Copi, 2001:21). Siguiendo a este autor, “los trabajadores de las ciencias han desarrollado vocabularios técnicos especializados para evitar las dificultades periféricas ligadas al lenguaje ordinario” (2001:21),3 como la vaguedad, la ambigüedad y el engaño.4
Teniendo en cuenta lo anterior, los objetivos de este ensayo son exponer algunos apuntes relacionados con la naturaleza simbólica y diagramática del razonamiento lógico-formal; explicitar la importancia del razonamiento simbólico y diagramático en el uso de la lógica (i.e. comprender qué significa conocer por medio de diagramas y símbolos) y, finalmente, como caso concreto de estudio, presentar un estudio sobre los diagramas de Venn y su utilidad didáctica, como adenda a esta última parte se presentarán algunas notas sobre el esfuerzo de la enseñanza de la lógica en el Nivel Medio Superior y Superior.
Lógica y representación simbólica (sistemas simbólicos)
El conocimiento simbólico es un tipo de conocimiento que se obtiene mediante la utilización y apoyo de estructuras semióticas o signitivas. Por supuesto, estas son ajenas a las presentaciones intuitivas.5 Según esta última condición, este tipo de conocimiento se opone al conocimiento directo o “intuitivo”.6 Efectivamente, como su nombre lo indica, una representación simbólica es una representación a través de signos, mientras que una presentación intuitiva se da de manera directa, dicho de otra manera, una representación simbólica ocurre cuando un contenido no se da directamente a nosotros como lo que es, sino como lo que significa (a través de signos que lo caracterizan).
Asimismo, las representaciones simbólicas se dan de manera indirecta. Ellas aparecen a modo de un representante, de un sustituto que actúa como una señal indicativa para un objeto (y sólo para ese objeto o sistema de objetos). Lo verdaderamente importante en este punto es, justamente, el carácter “subrogatorio” del conocimiento simbólico: “De hecho, todo el conocimiento humano es simbólico en la medida en que conocer presupone la construcción de estructuras simbólicas. Esta idea de conocimiento simbólico puede aplicarse al análisis de los aspectos cognoscitivos de la construcción de los sistemas formales”. (Esquisabel y Legris, 2003: 233).
Básicamente son cuatro las características principales del conocimiento simbólico: (I) los símbolos pueden llegar a ser independientes de su significado y, por tanto, de la interpretación que se les asigne; (II) los símbolos tienen un fin instrumental; (III) los símbolos pueden recibir diferentes interpretaciones y (IV), quizás la más destacable, los símbolos abren paso al conocimiento de estructuras formales y de sus propiedades. Por ejemplo, en el caso de la aritmética, las operaciones del cálculo no siempre remiten a los materiales originales o a la actividad más básica que es la de contar; antes bien, presentan formas cada vez más complejas y abstractas que hacen de la aritmética entera un compendio de medios artificiales. Otro caso es el de las ciencias formales donde la presentación de una representación simbólica o signitiva puede sustituir a una representación auténtica o intuitiva.
Así, lo verdaderamente importante en estos ejemplos es que un símbolo no es el objeto presentado, sino un sustituto de aquello que no puede ser presentado realmente, actúa, repetimos, como una señal indicativa para ese objeto. Empero, no funciona su conversa: una representación auténtica nunca podría sustituir una representación simbólica de ningún objeto y, por tanto, nunca podría contar como una representación simbólica de él. En resumen, se habla de representación simbólica cuando: 1) se da un “objeto” por medio de señales o signos unívocos; 2) cuando existe relación de concordancia entre el objeto representado auténticamente y el objeto representado simbólicamente -esto significa que la identidad de un objeto no cambia cuando se da o bien simbólicamente o bien auténticamente, lo que cambia es su modo de presentación-; 3) todo lo que puede enunciarse como verdadero en un objeto auténticamente presentado es verdadero del objeto presentado simbólicamente, y 4) tanto las representaciones auténticas como las simbólicas se pueden utilizar en juicios válidos sobre un objeto.
Ahora bien, la construcción de un conjunto cerrado de representaciones simbólicas constituye un sistema simbólico. Los sistemas simbólicos pueden ser entendidos como sistemas técnicos y, por tanto, tener un fin instrumental (Legris, 2001-2002, 2003, 2005). En tanto sistemas técnicos, los sistemas simbólicos se construyen de acuerdo con ciertos fines y partir de otro sistema de signos. Este último rasgo es decisivo en la medida en que la construcción de un sistema simbólico permite que sus signos sean manipulados, corregidos y aumentados. En este último sentido, los símbolos no sólo representan objetos, sino que también los producen (Legris, 2001-2002, 2003, 2005).
La introducción del concepto de sistema simbólico ha producido un salto metodológico importante dentro de las ciencias formales, esto se debe a que el conocimiento por medio de la manipulación de símbolos ha adquirido un lugar especialmente destacado en la estructura cognoscitiva humana (Legris, 2001-2002, 2005, 2012). Dicho con otras palabras: el conocimiento de las propiedades formales, junto con la mecanización de los procedimientos inferenciales, en la medida en que se manipulan los símbolos entendidos como objetos, nos ponen delante de un tipo de lenguaje artificial de manera tal que la correcta utilización de dichos sistemas hace más eficaz la solución de problemas típicos de las ciencias formales.
Efectivamente, los sistemas simbólicos se crean para resolver problemas. Así, un sistema simbólico es una suerte de herramienta cognoscitiva que nos permite observar reconocer trabajar inferir con propiedades que en los lenguajes naturales se vuelve imposible. Por esta razón, un sistema simbólico usa lenguajes “artificiales-analíticos” que sirven como modelos que pueden ser interpretados de manera “exacta” (Esquisabel y Legris, 2003:233, 235).
Por ejemplo, la construcción de sistemas algebraicos puede recibir diferentes interpretaciones, ya sea numéricas, geométricas, lógicas, etc., en cualquier caso, se destaca uno de los aspectos más importantes del conocimiento simbólico: la traslación o traducción de las estructuras simbólicas a diferentes dominios. Esto último es posible gracias al isomorfismo de un sistema simbólico que le permite la aplicación de un dominio a otro dominio que tenga la misma estructura7 (2003: 235 y ss.).
Según lo antes dicho cabe preguntar ¿cómo es posible visualizar lo anterior en el caso de la lógica formal? ¿Cómo ocurre su vínculo con el conocimiento simbólico? En primer lugar, todo sistema formal (S1) tiene la finalidad de representar la estructura formal de los diferentes dominios de entidades (Sn). Esto es posible en virtud de la abstracción de las peculiaridades de esos sistemas naturales. Según lo anterior, los sistemas formales serían, por tanto, sistemas simbólicos (Esquisabel y Legris, 2003). En segundo lugar, todo sistema formal (S1) tiene una función de interpretación del lenguaje como una estructura artificial (en S2). En tercer lugar, la relación de traducción de un sistema formal (S1) a otro (S2) puede considerarse como una representación del primero en el segundo. Como se observa, la manipulación del sistema S1 permite la afirmación de ciertas propiedades relevantes del sistema S2 cumpliendo así una función subrogativa.
Lógica y razonamiento diagramático
Existen numerosos sistemas diagramáticos, por ejemplo, los diagramas de flujo, diagramas de circuitos, diagramas electrónicos, etc. La diversidad de diagramas refleja su amplia gama de usos, desde aquellos que son coadyuvantes en las pruebas matemáticas hasta los que describen los sistemas físicos o fisiológicos. Según la literatura consultada, la noción de diagrama tiene, al menos, dos maneras de definirse: una definición amplia y una definición restringida. Una concepción amplia señala que casi cualquier tipo de inscripción que hace uso del posicionamiento espacial en dos o tres dimensiones es un diagrama (p.ej. gráficos, matrices, grafos, mapas conceptuales, croquis y mapas). Una concepción más restringida designa como diagramas a todas aquellas representaciones que mantienen ciertas reglas sintácticas y semánticas, incluidas las fórmulas algebraicas.
La última acepción es, quizás, la más adecuada para nuestros fines. Así, entenderemos por “diagrama” a la parte del razonamiento que está conectada con imágenes, modelos e íconos. Dicho de otro modo, un diagrama será para nosotros un signo complejo que incluye iconos, índices y símbolos. Esta idea venida de C.S. Pierce,8 advierte, además, que un diagrama es un signo que representa en nuestras mentes objetos y relaciones que conforman nuestra hipótesis. Un diagrama es, pues, una representación geométrica de relaciones entre entidades. Estas relaciones son espaciales y tienen un carácter topológico implicando, por tanto, un concepto de espacio (Lemon y Pratt, 1997). Efectivamente, un diagrama es un conjunto de objetos en el plano que denotan objetos en una estructura, cuyas mutuas relaciones espaciales y gráficas denotan relaciones en aquella. Asimismo, la estructura de un diagrama puede tener una correspondencia estrecha con lo que representan. Como bien apunta Legris (2012b), esta semejanza estructural a veces se ha calificado como un isomorfismo entre el diagrama y aquello que representa, es decir, ambos comparten una misma estructura. En todo caso, con esta semejanza estructural se ponen de relieve las diferencias entre la representación diagramática y la lingüística.
En el caso particular de los diagramas lógicos, estos son figuras geométricas bidimensionales con relaciones espaciales que son isomorfas con la estructura de las declaraciones lógicas. Según Castro Manzano, interpretando a Larkin y Simon (1987), “la diferencia entre las representaciones diagramáticas y sentenciales es que, debido a esta característica espacial, las primeras conservan explícitamente información sobre las relaciones topológicas, mientras que las últimas no” (2017b:247).
Dicho lo anterior, cabe preguntar ¿cómo es posible visualizar el aspecto diagramático en el caso de la lógica? Es posible mediante una lógica diagramática. Esta busca describir la sintaxis, la semántica, las pruebas, etc., de un determinado sistema diagramático. Precisamente, se le denomina razonamiento diagramático a la construcción de uno o varios diagramas mediante un sistema de representación, los mismo que a la experimentación y observación de los resultados de lo diagramas. (Bakker y Hoffmann, 2005). Para Hoffmann (2011) la función principal del razonamiento diagramático es “facilitar los procesos de pensamiento, individuales o sociales, en situaciones que son demasiado complejas para ser afrontadas exclusivamente por medios cognitivos internos” (p. 192). Dicho de otro modo, el razonamiento diagramático trata de facilitar y/o reducir la carga cognitiva tanto en las resoluciones individuales como colaborativas de los procesos de pensamiento. (Hoffmann 2011: 193)
El caso de los diagramas de Venn
Tomando en cuenta todo lo antes dicho, es posible aplicar las funciones del conocimiento simbólico y diagramático dentro del terreno de los diagramas de Venn y con ello evidenciar que estos satisfacen las necesidades del conocimiento simbólico a la vez que permiten una mejor comprensión lógica gracias a su carácter diagramático.
Según Shin (1994), “Venn”9 es un sistema lógico diagramático sólido y completo que representa de manera perspicaz el silogístico. Por tanto, puede definirse a través de un vocabulario, sintaxis y semántica bien definidos (p. 48). Dicho brevemente, el vocabulario diagramático de “Venn” está determinado por los siguientes elementos: la curva cerrada, el rectángulo, el sombreado, la X y la línea10 (Shin, 1996). Con este vocabulario, un diagrama en “Venn” se define como una combinación o colección finita de elementos agrupados en un universo cerrado U. Por ejemplo, los círculos de los diagramas de Venn representan conjuntos y las combinaciones superpuestas de los círculos representan combinaciones entre conjuntos. Si se usan correctamente, se pueden hacer inferencias válidas con estos diagramas, y si se usan incorrectamente, pueden ser la fuente de inferencias inválidas.
En efecto, “para analizar tales estándares, se podría construir un sistema formal de diagramas de Venn donde la sintaxis, las reglas de inferencia y la noción de consecuencia lógica se hayan hecho precisas y explícitas, como se hace en el caso de la lógica de primer orden (Hammer y Danner, 1996:109). En cualquier caso, en el sistema de Venn se trata de encontrar el tipo de operación, con dichos diagramas, que refleje la información contenida en una o varias proposiciones. Previamente se determinar el número total de términos implicados. De acuerdo con este número, se escogerá el diagrama correspondiente. A continuación, se opera con dicho diagrama según la información que proporcionan las proposiciones iniciales, y de acuerdo con el “método de eliminación” que Venn propone, esto es, dada una proposición, se tratará de determinar qué “compartimento” o “clase” no contendrá ningún elemento a fin de realizar alguna marca identificativa en dicho compartimento del diagrama (el sombreado). Si hay más proposiciones que añaden información, entonces se buscan otros compartimentos con los cuales podamos tener la certeza de que son compartimentos o clases vacías (no contienen ningún elemento) (Casas Cañas 2012:104-105).
Los diagramas definidos a continuación consistirán en un rectángulo dibujado en un plano bidimensional en el que se dibujarán dos círculos junto con sus cuatro combinaciones que representan la intersección, las dos diferencias y el complemento de la unión.11 Dicho con otras palabras, este diagrama consta de cuatro regiones mínimas12 (Hammer, 2001:396) que se representan aquí:
Los sistemas diagramáticos, como los diagramas de Venn, también pueden presentarse a la manera de un cálculo formal, es decir, sobre la base de reglas sintácticas y semánticas. Así, por un lado, las reglas sintácticas determinarán cuando un diagrama es un “diagrama bien formado”, es decir, cuando un símbolo complejo es aceptado como un diagrama. Por otro lado, las reglas semánticas indicarán las entidades a las que se refieren los diagramas, y establecerán una relación de consecuencia lógica para el sistema lógico diagramático (Legris, 2012b). Todo lo anterior nos conduce a una definición de derivabilidad respecto de un sistema diagramático, a la vez que nos permite establecer la adecuación del sistema diagramático con una noción semántica de validez. Según lo anterior, los diagramas de Venn bien formados podrían resumirse mediante las siguientes cuatro construcciones:
Cualquier n círculos dibujados para superponerse (overlap) en todas las combinaciones como se describe en la sección anterior y etiquetada con n nombres es un diagrama de Venn bien formado.
Dado cualquier diagrama de Venn, el resultado de agregar un ‘o’ a cualquier región mínima que no contenga un ‘o’ da como resultado un diagrama de Venn bien formado.
Dado cualquier diagrama de Venn, el resultado de agregar una cadena ‘x’ a cualquier región que no tenga una cadena ‘x’ da como resultado un diagrama de Venn bien formado.
Nada más es un diagrama de Venn bien formado (Hammer, 2001: 400).
Tomando en cuenta lo anterior, podríamos decir que los diagramas de Venn cumplen con una función operativa. También es posible decir que algunas de las funciones epistemológicas del conocimiento simbólico se cumplen en la lógica de Venn. En especial, los diagramas permiten visualizar el significado de la noción epistemológica de extensión indefinida. Siendo esto así, pensemos en el diagrama que representa las proposiciones de la forma Todo A es B.
En este diagrama, “se simbolizan, a través del uso de sombreados, que no existen As que no son Bs; no obstante, en el mismo diagrama, representamos también que no sabemos si existen As que son Bs, así como también representamos que no sabemos si existe Bs que no son As” (Ramos Mendonça 2013:68). Las informaciones sobre lo que no sabemos acerca de la extensión de los términos involucrados son representadas por la ausencia de signos en áreas específicas del diagrama.
Ahora bien, todo lo anterior -esto ya forma parte del razonamiento diagramático- no es acerca de la figura dibujada, sino acerca de los conceptos así representados con las figuras en tanto signos. Esto significa que la utilización de los diagramas de Venn no es acerca de círculos, sino acerca de relaciones entre conceptos (subordinación, exclusión, relación, etc.) que tales círculos, mediante marcaciones, representan, incluidas las propiedades topológicas de formas circulares que se solapan13 (Lasalle Casanave, 2003).
De acuerdo con lo anterior, el razonamiento diagramático es un método de deducción que se define a partir de la operación con diagramas. Así, podemos decir que los diagramas de Venn son una representación externa de relaciones que se construyen de acuerdo con reglas y convenciones, y por medio de los elementos y relaciones disponibles, en un determinado sistema de representación. En tanto sistema de representación, los diagramas de Venn proporcionan los medios y posibilidades de construir y manipular representaciones espaciales de relaciones.
La función didáctica de los diagramas de Venn
No cabe duda que los esquemas facilitan la aprehensión de contenidos y sirven para establecer conexiones de sentido. Los esquemas son utilizados por los agentes educativos como un recurso, una técnica o una estrategia didáctica. Generalmente un docente solicita a sus estudiantes evidencias de lectura, pero el objetivo a seguir es la comprensión (psicológica o pragmática) del contenido. Una manera apropiada de hacerlo es solicitando esquemas a los estudiantes. No obstante, cada esquema responde a un propósito preciso. Por tal razón conviene que el docente conozca de primera mano la lectura que el estudiante ejecutará para demandarle un determinado tipo de esquema que corresponda lógicamente al contenido de la lectura.
Pedagógicamente hablando los esquemas son recursos de aprendizaje. Si estos obedecen a un plan que persigue un objetivo de aprendizaje se les denomina estrategia didáctica. El carácter visual de los esquemas los hace amable para los estudiantes porque sintetiza un proceso racional. Evidentemente existen muchos tipos de esquemas y cada cual responde a un objetivo; sin embargo, los esquemas comparten el criterio lógico. No hay esquema que no obedezca a una lógica específica. Por ejemplo, las redes semánticas establecen relaciones entre palabras y los mapas conceptuales visualizan relaciones entre las ideas y conceptos organizándolos jerárquicamente. Este último esquema guarda una estrecha relación de parentesco con el árbol de Porfirio. De hecho, podría decirse que los mapas conceptuales derivan del árbol de Porfirio.14
En el contexto educativo de la filosofía, en concreto, en la enseñanza de la lógica, el estudiante de filosofía aborda como tema de estudio en el pregrado los diagramas de Venn y el árbol de Porfirio. Así, por ejemplo, los diagramas de Venn forman parte de las etapas de la metodología anunciada por escrito en el programa de estudios. Esto significa que un primer paso para el estudiante consiste en aprender a elaborar argumentos y silogismos, un segundo paso estriba en la formalización de estos razonamientos. Para ello el estudiante aprende a reemplazar enunciados por símbolos que operan como alfabeto del lenguaje formal, facilitando una tarea que sin el recurso de la simbolización se tornaría complicada. Cuando los estudiantes aprenden estos menesteres, aplican estas estructuras lógicas por medio de diagramas de Venn. Mostremos un poco más cómo los diagramas de Venn obedecen a un proceso de enseñanza-aprendizaje cuando operan como un proceso de razonamiento lógico.
De entrada, en su función didáctica, los diagramas de Venn permiten a los estudiantes comprender relaciones, captar juicios y silogismos e incluso es un apropiado recurso mnemotécnico. Como es evidente, todas estas operaciones mentales son necesarias para la adquisición y desarrollo de aprendizajes. Son también evidencias de aprendizaje. En cuanto a su función lógica representativa, se observa que los diagramas de Venn pueden representar enunciados, es decir, esquematizan una proposición categórica, representando ya sea una proposición universal afirmativa, una proposición particular afirmativa o negativa. Incluso, dando un salto de nivel abstractivo, simbolizan enunciados.
En los diagramas de Venn se observan relaciones de inclusión y exclusión de clases, y, fundamentalmente, aquellos se tornan efectivos para hacer patente la validez o invalidez de un silogismo. Para ello se ha de considerar los términos del silogismo como expresiones de una clase. A fin de ejemplificar cómo los diagramas de Venn comprueban la validez o invalidez de un silogismo veamos la siguiente figura. El silogismo que sirve de ejemplo es el siguiente:
Todo reloj es un instrumento de tiempo
Todo “Casio” es un reloj
Por tanto, todo “Casio” es un instrumento de tiempo.
En este sentido, el silogismo de la primera figura, modo AAA, se representa simbólicamente con el siguiente diagrama.
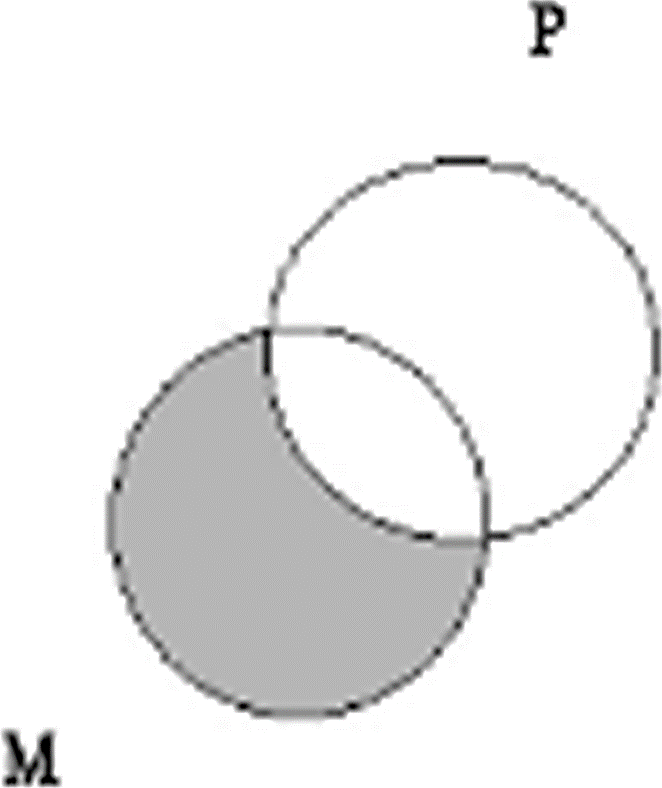
La representación de la conclusión ha de obtenerse a partir de la diagramación de las premisas, es decir, la conclusión ha de estar contenida en las premisas. De esta manera, se puede comprobar la validez del silogismo mediante los diagramas. Para observar el diagrama de cada término del silogismo, en la premisa mayor se sombrea como clase vacía todo M que no está contenido en P.
Como lo muestra el diagrama se indica que no hay M que no esté contenida en P.
En la premisa menor se sombrea como clase vacía S, que no está contenida en M, ya que solo hay S que son M.
Si el argumento es válido, la representación de la conclusión deberá estar implicada a partir de la esquematización de ambas premisas. Con lo anterior podemos afirmar que los diagramas de Venn cumplen una función didáctica que es inmanente a su función lógica, puesto que en su pretensión de establecer relaciones excluyentes e incluyentes y demostrar la validez o invalidez de un silogismo se muestra una pretensión didáctica: 1) captar la atención del estudiante mediante figuras y colores; 2) motivar el aprendizaje del educando al presentar un reto creativo de simbolización; 3) mostrar al alumno de manera asequible y entendible relaciones entre los conjuntos, a fin de que con ello se haga evidente el sentido del diagrama y del proceso de razonamiento, y 4) desarrollar en el estudiante el pensamiento crítico, es decir: “la capacidad y disposición de llegar a conclusiones y evaluarlas con base en las pruebas” (Eggen & Kauchak, 2012: 106-107).15
De manera análoga a la comprobación de las soluciones de las ecuaciones matemáticas los diagramas de Venn demuestran argumentos deductivos. Gracias al carácter visual de los diagramas de Venn los estudiantes pueden entender los procesos de razonamiento que se establecen en él mediante la visualización de las relaciones entre sus conjuntos, en especial se favorece el aprendizaje de los estudiantes en los que predomina el estilo visual, en la medida en que estos recuperan la información en forma de imagen.
Esta propiedad de los diagramas de Venn facilita la retención de la información y su comprensión entre los estudiantes, incluso los aprendizajes logrados por este medio adquieren un estatus de significatividad para los estudiantes, ya que es más fácil y rápido recordar una imagen de un argumento que un argumento desarrollado por escrito. A partir del componente visual de los diagramas de Venn los estudiantes pueden empezar a desplegar un argumento que fue previamente comprendido mediante esta estrategia didáctica. Finalmente, consideramos que en la enseñanza de la lógica se requieren más estrategias didácticas de este tipo. Esto se señala en parte en la siguiente sección.
Adenda. Los intereses de aprendizaje y los esfuerzos de enseñanza de la lógica en México
El primer contacto que tenemos con la lógica en un sentido académico generalmente ocurre en el Nivel Medio Superior. En el bachiller del Sistema Educativo Mexicano, se ofertan algunas asignaturas de corte filosófico, entre ellos “Ética”, “Doctrinas filosóficas”, “Filosofía” y “Lógica”. Naturalmente, el contenido alusivo a la lógica es el básico. Las antologías y libros utilizados en esta modalidad educativa tienen la estructura de un manual, pues ofrecen definiciones, ejemplos y ejercicios. Sabemos que los manuales pueden ser muy logrados, pero también pueden no serlo. Ha de tomarse en cuenta que para su elaboración se requiere de una cierta competencia pedagógica que los lógicos, por lo regular, no tienen. Raymundo Morado señala las limitaciones en el uso de las técnicas didácticas en la enseñanza de la lógica: “Algunos diagramas lógicos, algunos versos mnemónicos, algunas observaciones sobre la enseñanza de la Lógica al inicio de los tratados (que a menudo eran tanto artículos de investigación como libros de texto). Mucho trabajo importante, útil e interesante en la teoría de la Lógica y no mucho sobre su didáctica” (2011:103).
Se trata del uso de técnicas muy limitadas para la enseñanza de la lógica, pues no alcanzan a erigirse como estrategias de aprendizaje de una cierta actividad pensante y razonada (no se cuestiona aquí el procedimiento de un ejercicio lógico, sino las técnicas didácticas que acompañan a esos ejercicios), su carácter es memorístico. De esto se colige que el aprendizaje de la lógica no se obtiene o desarrolla siguiendo una receta de cocina que se ha denominado manual de lógica, esto genera “planes de estudios anticuados, profesores frustrados y alumnos vacunados contra la lógica” (Morado, 2011:103). Así también sucede en el Nivel Superior en donde se trabajan con estas limitadas técnicas a través de un manual, salvo casos donde algunos profesores implementan un contenido más especializado en lógica, mas no especializado en la didáctica de la lógica. Eso falta por abonar y es una preocupación latente del Taller de Didáctica de la Lógica desde 1996 y de la Academia Mexicana de Lógica desde 2003 (Morado, 2011).
Por otro lado, siguiendo a Morado (2005), en las carreras universitarias como sistemas computacionales, matemáticas y filosofía por situar algunos casos, trabajan un cierto tipo de lógica que responde a sus respectivos intereses: “En ciencias de la computación utilizas lógicas polivalentes” (Morado, 2005:11), porque representan múltiples valores; no son valores de verdad en el sentido de la lógica clásica.
En la licenciatura en Filosofía, al menos en el contexto mexicano, se trabaja con distintos manuales de lógica, los cuales responden a distintas lógicas, ya sean clásicas o no clásicas o de otro tipo, preferentemente la mayoría de los lógicos se forman en lógica clásica. En esta disciplina y dependiendo de la tradición o trayectoria de sus académicos o de modas, se enfatiza la enseñanza de un cierto tipo de lógica.
Una diferencia importante en esta modalidad educativa, es que los profesores pueden elaborar sus propios manuales o libros de lógica con un enfoque preciso. Respecto a este asunto de la precisión en el enfoque con el que se enseña lógica, depende mucho de la preocupación que se tenga. Sirva la siguiente cita recogida de una entrevista que Ariel Campirán hace a Raymundo Morado en el imaginario de una alumna ficticia pero interesada en otras posibilidades de la lógica:
Si [a la alumna] le preocupa mucho eso de que «todo es verdadero o falso», entonces puede irse a sistemas en donde eso no se da, donde no funciona el tercio excluso. Puede, por ejemplo, creer que hay proposiciones que no son ni verdaderas ni falsas, sino todo lo contrario: como “la paradoja del mentiroso” o como ciertas proposiciones matemáticas indemostrables; entonces puede irse a una lógica polivalente o a una intuicionista.
O podría querer rechazar el principio de no contradicción, ya que ¿por qué tiene que ser un solo valor?, ¿por qué no tener ambos valores?, ¿por qué no tener una cosa que es verdadera y falsa al mismo tiempo? Tal vez la alumna tenga preocupaciones sobre la dialéctica hegeliana o el marxismo, o sistemas postmodernos, y quiera decir que algo es verdadero y falso. Entonces viola el principio de no contradicción; puede irse a lógicas contradictoriales, a lógicas paraconsistentes porque tiene ese interés.
Depende de cuál sea su preocupación. Si cree que la física cuántica viola el principio de distributividad, puede buscar una lógica no distributiva como las lógicas cuánticas. Si cree que la LC comete falacias de relevancia, puede estudiar un sistema de lógica relevante o de lógica de la relevancia. La idea es que si tienes una objeción o un problema con la LC es probable que alguien haya explorado la posibilidad de rechazar ciertos supuestos. Mencioné antes que los dominios de discurso no pueden ser vacíos. Bueno, ¿qué pasa cuando sí son vacíos? ¿Qué sistema lógico aparece? Pues, un sistema de lógica libre de presupuestos existenciales. Entonces, en general la pregunta es ¿Para qué quiere estudiar más lógica esa alumna? ¿Quiere estudiarla más para profundizar en lo que ya tiene? o ¿quiere estudiarla más para resolver ciertas dudas o preocupaciones que le ha ocasionado? A lo mejor le conviene ver sistemas rivales. O a veces simplemente quiere aplicarla, utilizarla en ciertos dominios: si quiere usar la Lógica para el Derecho, puede ver lógicas jurídicas o lógicas deónticas. Si quiere utilizarla para Teoría del Conocimiento, puede estudiar lógicas epistémicas (Morado, 2005:12-13).
Como puede notarse en la formación en lógica la (o el) estudiante puede optar por estudiar desarrollos contemporáneos de la lógica clásica o puede ver algunas extensiones para completarlas, también puede ver lógicas rivales a la lógica clásica (Morado, 2005).
En la Universidad se trabajan con una infinidad de textos que atienden las preocupaciones de la estudiante imaginaria de Raymundo Morado, por ejemplo, si el interés estriba en estudiar una lógica libre de presupuestos ontológicos se consulta el curso de lógicas libres de Bencivenga; si interesa un curso de lógica modal, como un añadido de la lógica clásica se revisan los trabajos de Lewis y Langford. De acuerdo con Raymundo Morado (2005), los autores señalados muestran que se puede empezar con lógica modal y la lógica clásica proposicional sale como corolario (Morado, 2005:8).
Nos parece muy valioso considerar esta recomendación en la enseñanza de la lógica. Raymundo Morado (2005) sostiene que puede comenzarse a enseñar lógicas intuicionista o modal y al quitarle o agregarle cosas puede perderse decibilidad, consistencia o completud, y puede decírsele al estudiante que tiene ahí una lógica clásica que sí posee esas propiedades metateóricas. Por razones históricas y teóricas se enseña lógica clásica porque es la más conocida y mejor trabajada (Morado, 2005:16). Además, también se estudian los libros originales de Aristóteles y de otros filósofos medievales, modernos y contemporáneos. Conforme los estudiantes avanzan en sus estudios universitarios el nivel de los contenidos va en ascenso y si estudian un posgrado con énfasis en lógica, naturalmente se forman con un material más especializado.
Como conclusión, se puede decir que la enseñanza de la lógica no se enmarca en un contexto meramente formal o situado en los marcos legales del plan de estudios, sino que existen otros escenarios formativos no formales como congresos y talleres. En los congresos los estudiantes y especialistas en lógica asisten para exponer sus propios sistemas o contribuciones al terreno de la lógica. En estos congresos incluso pueden ofrecerse talleres de lógica. Uno de los congresos en los que se exponen trabajos de diversa índole sobre la lógica en México es el que organiza la Academia Mexicana de Lógica (AML).











 nueva página del texto (beta)
nueva página del texto (beta)