Artículos

 

Logicismo y analiticidad. Frege y Carnap dos propuestas logicistas

 

Logicism and Analyticity. Frege and Carnap, two Logicians Proposals

 

Jesús Jasso Méndez*

 

* Profesor-investigador, Academia de Filosofía e Historia de las Ideas, UACM-Tezonco. Profesor de Asignatura, Colegio de Filosofía, FFyL, UNAM.

 

Fecha de recepción: 13 de febrero de 2013
Fecha de aprobación: 22 de abril de 2014

 

Resumen

Distintos programas de investigación en filosofía han definido las nociones de analiticidad y aprioricidad. Perspectivas contemporáneas: Boghossian (2000), Peacocke (2000), Kitcher (1980, 2000), Horwich (2000) —sólo por mencionar algunos casos— enfrentan el problema de definir la extensión de tales conceptos. La finalidad del presente artículo es: ofrecer al lector en un solo artículo útil, un análisis fino y delimitado de las definiciones logicistas paradigmáticas de la analiticidad que originan las discusiones contemporáneas: Frege (1879, 1874) y ii. Carnap (1935, 1947). De esta manera, el lector estará en condiciones conceptuales de seguir adecuadamente la polémica clásica y contemporánea que al respecto, en filosofía del lenguaje, filosofía de la lógica y la epistemología se encuentra disponible.

Palabras clave: Semántica, Analiticidad, Aprioricidad, Logicismo, Frege, Carnap.

 

Abstract

Different research programs in philosophy have defined the notions of analyticity and apriority. Contemporary perspectives: Boghossian (2000), Peacocke (2000), Kitcher (1980, 2000), Horwich (2000) —just to mention some cases— face the problem of defining the extension of such concepts. The purpose of this paper is: to offer the reader, in a single useful article, a fine and delimited analysis of the paradigmatic logicist definition of analyticity that cause the contemporary discussions: Frege (1879, 1874) and ii. Carnap (1935, 1947). In this way, the reader will have the conceptual tools to follow properly the classical and contemporary controversy available on this matter, in philosophy of language, philosophy of logic and the epistemology.

Key words: Semantics, Analyticity, Apriority, Logicism, Frege, Carnap.

 

INTRODUCCIÓN

El problema de caracterizar las nociones de analiticidad y aprioricidad en filosofía no es una empresa nueva. Distintos programas de investigación en filosofía del lenguaje, filosofía de la lógica y epistemología, han brindado diferentes formas de particularizar este problema ex. gr. Frege (1884, 1879), Russell (1919), Carnap (1935, 1937, 1947), Quine (1951), Kripke (1972).¹

Este trabajo forma parte de una investigación más amplia en torno a las nociones de analiticidad, aprioricidad y necesidad. Por cuestiones de extensión, en esta ocasión mi finalidad conceptual se restringe a presentar dos contenidos: A. La aritmética y la analiticidad de acuerdo con el programa logicista de Frege; B. La analiticidad de acuerdo con el programa sintáctico y semántico de Carnap. Para lograr (A) y (B), mi estrategia de presentación será la siguiente.

El artículo lo he dividido en tres secciones.

En I. PRELIMINARES, identifico el objeto de aplicación primaria de las distinciones analítico/sintético y a priori/a posteriori. Con este trabajo conceptual, el lector podrá distinguir no sólo la naturaleza filosófica de cada dicotomía; adicionalmente podrá ver cómo para el logicismo la definición de la analiticidad y de la aprioricidad están fuertemente vinculadas.

En II. LA ANALITICIDAD EN LA ARITMÉTICA: SEMÁNTICA DE FREGE analizaré puntualmente en qué términos Frege atribuye analiticidad a los enunciados aritméticos y lógicos —y, sólo a ellos—. Consideraré Die Grunlagen der Arithmetik (1884), particularmente la <<Einleitung>> y las secciones 1-4 y 12 y algunos pasajes de su Begriffsschrift (1879).

En III. CARNAP: UNA PROPUESTA SINTÁCTICA Y SEMÁNTICA DE LA ANALITICIDAD descifraré la extensión del predicado 'ser analítico' a partir de <<Logical Syntax of Language>> (1935) y Meaning and Necessity (1947) i. e. de acuerdo con los programas sintáctico y semántico de Carnap.

El contenido de (I), (II) y (III) contribuirá a que el lector se encuentre en condiciones conceptuales satisfactorias para seguir, desde la base, la polémica clásica y contemporánea que respecto a la extensión de la noción de analiticidad se encuentra disponible actualmente en la literatura de la filosofía del lenguaje, la filosofía de la lógica y la epistemología.

 

PRELIMINARES

Una de las rutas para clarificar nociones como analiticidad y aprioricidad consiste en explicar la relación entre dos distinciones conceptuales: i. analítico/sintético, ii. a priori/a posteriori.

En principio, la distinción analítico/sintético es una disimilitud semántica, i. e. una distinción que se explica en términos del significado de los enunciados de un lenguaje (L). El significado es entonces el objeto primario al que se aplica esta distinción. Por su parte, la distinción a priori/a posteriori se trata de una disimilitud de tipo epistemológico, i. e. podemos predicar de un enunciado su aprioricidad o aposterioricidad en términos del tipo de justificación de las verdades que tales enunciados expresan. El conocimiento es entonces el objeto primario al que se aplica esta disimilitud.

Distinguir los objetos de aplicación primaria de la analiticidad y la aprioricidad es importante pues nos permite aplicar un criterio conceptual estándar útil para identificar los compromisos filosóficos-conceptuales que adquieren los enfoques logicistas y semantistas.

Específicamente, los programas de Frege (1979) (1984) y Carnap (1935) (1947) trataron de:

i. ofrecer una definición de analiticidad y aprioricidad;

ii. proponer criterios de identidad para distinguir enunciados analíticos y verdades a priori;

iii. establecer las posibles relaciones entre 'ser analítico' y 'ser a priori' considerando coextensionalidad entre ambos predicados, pero al tiempo, presuponiendo una independencia entre ellos sin trivializar la naturaleza filosófica de cada predicado.

A partir de la distinción estándar entre analiticidad y aprioricidad y considerando (i), (ii) y (iii), las siguientes preguntas conducirán el desarrollo de las siguientes secciones:

1. ¿Cuál es la naturaleza de la conexión entre la analiticidad y la aprioricidad de acuerdo con los dos proyectos logicistas arriba señalados?

2. ¿En qué sentido hablar de la analiticidad implica decir algo relevante de aprioricidad —y, viceversa?

3. ¿Existe alguna relación entre algún tipo de definición de las nociones con aquellos criterios de identidad que nos permiten identificar enunciados analíticos y verdades a priori?

 

II. LA ANALITICIDAD EN LA ARITMÉTICA: SEMÁNTICA DE FREGE

Frege propone una explicación del predicado 'ser analítico' como una consecuencia natural de su programa logicista. De acuerdo con el logicismo los enunciados matemáticos son reducibles a enunciados lógicos. Esta reducción considera dos aspectos: una reducción conceptual² y una reducción por decidibilidad³. Al respecto, Hintikka (2009) señala:

...de acuerdo con el logicismo, la matemática puede ser reducida a la lógica.

(a) Todo concepto de las matemáticas, i.e., de la aritmética, álgebra y análisis, pueden ser definidos en términos puramente lógicos.

(b) Todos los teoremas de las matemáticas pueden ser deducidos desde estas definiciones por medio de los principios de la lógica [...] (Hintikka, 2009: 271)⁴

La tesis reduccionista considera entonces dos condiciones: la lógica es capaz de definir el lenguaje matemático y la lógica es capaz de probar el conjunto de verdades matemáticas. Una consecuencia de esta reducción será la atribución transitiva de propiedades semánticas y epistemológicas desde los enunciados lógicos hacia los enunciados matemáticos.

De acuerdo con Frege, los enunciados aritméticos son los más generales, pues el establecimiento de su verdad se sigue únicamente de leyes generales de la lógica y definiciones, sin incluir en la derivación algún tipo de contenido extra-lógico. La noción de generalidad viene de la lógica. Si el rango de aplicación de las verdades que expresan los enunciados aritméticos abarcan:

... no sólo lo actual, no sólo lo intuible, sino todo lo pensable", ... entonces Frege no puede pensar en otra fuente de tan tremenda generalidad, que no sea la lógica misma, la ciencia de "lo pensable" por excelencia. Entonces, tanto la afirmación que la aritmética lo abarca todo, como la afirmación que esta generalidad viene de la lógica, indican en qué sentido debe entenderse el dictum que la aritmética es analítica (Cfr. Morado, 1987: 46-47).

En consecuencia, si las verdades lógicas son las más generales al considerarse paradigmáticamente analíticas y la justificación de su contenido a priori, entonces, los enunciados aritméticos al ser reducibles a términos lógicos, deberán considerarse, como bien lo señala Morado (1987), también generales al ser analíticos y su verdad se considerará a priori.

La 'analiticidad' entonces no refiere a la relación kantiana entre el contenido conceptual del predicado como contenido en el contenido conceptual del sujeto,⁵ sino a la propiedad que tiene un enunciado, o bien, i. de ser deducido a partir de leyes generales de la lógica y definiciones admisibles en el sistema formal; o bien, ii. de funcionar como axioma lógico. Si lo anterior es correcto, la definición de analiticidad coincide con el segundo aspecto de la tesis logicista-reduccionista: "los teoremas de las matemáticas pueden ser deducidos desde estas definiciones [lógicas] por medio de los principios de la lógica" (Hintikka, 2009: 271); pero en este caso diremos: AF:⁶ un enunciado será analítico sii es consecuencia lógica⁷ de leyes lógicas generales y definiciones, o bien es una axioma lógico. De tal suerte, si los enunciados aritméticos son decidibles en términos lógicos, entonces, tales enunciados serán necesariamente analíticos, luego forman parte de la clase de los enunciados más generales (Cfr. Morado, 1987: 46-47). Analicemos (AF).

Una preocupación filosófica constante de Frege es el significado o contenido de las expresiones de un lenguaje. En Die Grundlagen der Arithmetik (1884) encontramos una investigación semántica de tipo formal. Para Frege el estudio semántico se trata de un estudio lógico.⁸ De acuerdo con el contenido de la "Einleitung" y de las secciones 1-4 de Die Grundlagen los enunciados matemáticos tienen una legitimidad independiente de los hechos empíricos y de las representaciones subjetivas de los individuos:

...la aritmética no tiene absolutamente nada que ver con las sensaciones. Tampoco con las imágenes mentales que confusamente surgen de impresiones sensoriales anteriores. Lo indeciso e indeterminado que ostentan todos estos desarrollos entra en fuerte contraste con la determinación y solidez de los conceptos y objetos matemáticos (Frege, [1884] (1972): 110).

En la base de esta consideración se encuentra un intento por demostrar que los enunciados de la aritmética son analíticos, i.e satisfacen al menos una de las siguientes dos condiciones: i. no dependen de la experiencia y presuponen únicamente definiciones y las leyes generales de la lógica para su demostración, ii. son axiomas lógicos. La analiticidad para Frege consiste entonces en un tipo de predicado proposicional justificable en función de un ejercicio deductivo.

La versión fregeana sobre la analiticidad relaciona, a partir de la prueba lógica, el estatus epistemológico de la justificación de las verdades matemáticas, con la naturaleza semántica de los enunciados que expresan o contienen tales verdades. En otras palabras, relaciona la propiedad semántica analítica de los enunciados matemáticos con la condición a priori de su verdad:

Estas distinciones entre a priori y a posteriori, entre sintético y analítico, atañen... no al contenido del juicio, sino a la justificación para emitirlo. Ahí donde falta esta justificación, falta también la posibilidad de toda distinción...Cuando se dice que una proposición es analítica o a posteriori no se juzga sobre las relaciones psicológicas, fisiológicas y físicas que pudieran haber hecho posible la formación de la proposición en nuestra conciencia; tampoco sobre cómo alguna otra persona, tal vez erróneamente, haya llegado a tenerla por verdadera, sino por la razón más profunda en que descansa la justificación que la toma por cierta (Frege, [1884] (1972), secc. 3,: 116-117).

En consecuencia, la distinción a priori/a posteriori, como la distinción analítico/sintético, conciernen al contenido del enunciado en tanto éste incluye una referencia a la justificación de la emisión de tal expresión, a su prueba lógica. La prueba lógica entonces funciona como un dispositivo sintáctico que permite decidir la condición semántica analítica de un enunciado i. e. si este es consecuencia lógica de leyes lógicas generales y definiciones o bien es un axioma lógico, en el marco de una demostración; y, al tiempo, funciona como un dispositivo epistemológico tal que al ser un enunciado probado exclusivamente por medio de herramientas sintácticas, al margen de cualquier hecho extra-lógico, se considera que expresa una verdad a priori. Esto es lo que se conoce como la coextensionalidad en Frege entre analiticidad y aprioricidad:

...la pregunta debe apartarse del campo de la psicología y adscribirse al de la matemática, cuando se trata de una verdad matemática. El problema es el de encontrar su prueba y seguirla hasta las verdades más primitivas. Si en este camino sólo se encuentran definiciones y leyes lógicas generales, entonces se trata de una verdad analítica... (Frege, [1884] (1972), secc. 3,: 116-117).

tal que un enunciado es analítico sii es un teorema lógico, luego al ser la prueba lógica la evidencia de su verdad ésta quedará justificada a priori⁹

Adicionalmente, si consideramos ahora la justificación fregeana para la validez de reglas como modus ponens —en Conceptografía (1879)— se sugiere un segundo tipo de condición para atribuir analiticidad correctamente. Un enunciado es analítico sii resulta lógicamente válido con base en las condiciones de asertabilidad que definen las conectivas que en dicha enunciado figuran. Se trata de una interpretación semántica técnica de los enunciados, la cual establece la relación entre las fórmulas y parte de lo que éstas significan i.e. lo que ahora llamaríamos sus condiciones de verdad (Cfr. Frege [1879] (1972), secc. 5 y 6: 17-22). En consecuencia, de acuerdo con Frege un enunciado será analítico o bien por ser consecuencia lógica de leyes lógicas generales y definiciones —incluyendo el caso de ser un axioma lógico—, o bien porque la validez de su forma es consecuencia de las interpretaciones posibles de las constantes lógicas que constituyen su estructura.

Bajo estas dos caracterizaciones de la analiticidad, la propiedad analítica de un enunciado consiste en: i. señalar un sentido de generalidad i.e. advertir el lugar que ocupan los enunciados en un sistema teórico a partir del rango de aplicación de su verdad y, ii. en el tipo de demostración de tal enunciado. El proyecto logicista de Frege consiste justamente en demostrar la analiticidad de los enunciados de la aritmética a partir de (i) y (ii). El tipo de justificación lógica de un enunciado determina su rango de generalidad. Si ha de hablarse de algún tipo de definición de analiticidad en Frege, tal aspecto, implica considerar criterios de identificación y justificación de enunciados verdaderos.

Bajo este tipo de consideraciones, la distinción analítico/sintético es una distinción de orden lógico-semántico y no gramatical. La pregunta sobre la naturaleza de las distinciones analítico/sintético y a priori/ a posteriori de las verdades matemáticas no tiene que ver con consideraciones de orden psicológico, sino con aquellas referidas sólo a ejercicios formales deductivos y a la caracterización de las fórmulas que aparecen en una prueba lógica. La naturaleza de las proposiciones depende, entonces, no del contenido empírico del enunciado sino de su justificación en un sistema formal abstracto:

...si es imposible llevar a cabo la prueba sin utilizar verdades que no sean de naturaleza lógica general, sino que pertenezcan a un campo especial de conocimiento, entonces se trata de una proposición sintética. ...para que una verdad sea a posteriori, se exigirá que su prueba no pueda producirse sin apelar a situaciones fácticas, esto es, a verdades que no se puedan probar y que no sean generales, a verdades que contengan asertos sobre objetos determinados. Si por el contrario, es posible producir la prueba totalmente en base con leyes generales, que por su parte ni necesitan ni admiten prueba, entonces la verdad es a priori (Frege, , [1884] (1972), secc. 3,: 117).

En suma, cinco consideraciones nos permiten caracterizar la propuesta logicista de Frege en torno a la analiticidad y su relación con la aprioricidad:

a. Los teoremas de la aritmética se demuestran en la teoría formal a partir de pasos de inferencia desde proposiciones lógicas iniciales enumeradas. El ejercicio consiste en encontrar la prueba de un enunciado aritmético y seguirla hasta las verdades más primitivas.

b. Si en la demostración encontramos únicamente definiciones y leyes lógicas generales —primer sentido de analiticidad—, entonces se trata de una verdad —segundo sentido de analiticidad— con el mayor grado de generalidad expresado por un enunciado analítico.

c. Si en la prueba encontramos un enunciado de naturaleza no lógica que pertenezca a un campo científico distinto, entonces estamos frente a un enunciado sintético.

d. Si la prueba del enunciado no procede sin apelar a situaciones de orden fáctico i. e. a verdades que no se pueden probar exclusivamente con el lenguaje formal y, que por tanto, no sean generales, sino verdades cuyo contenido se refiere a objetos y relaciones entre particulares, entonces estamos frente a una verdad a posteriori.

e. Si la demostración se obtiene únicamente a partir de leyes generales de la lógica que, por su parte, no necesitan ni admiten prueba, entonces estamos frente a un enunciado analítico y a una verdad a priori (coextensionalidad entre dos propiedades de los enunciados aritméticos cuya naturaleza filosófica es de diferente orden).

 

CARNAP: UNA PROPUESTA SINTÁCTICA Y SEMÁNTICA DE LA ANALITICIDAD

La teoría formal de Carnap en "Logical Sintax of Language" (1935) y en Meaning and Necessity (1947) ofrece una caracterización sintáctica y semántica, respectivamente, del tipo de enunciados que figuran en un lenguaje S. Los argumentos en ambos casos no tienen el propósito de ofrecer un criterio de identidad de la analiticidad, ni un tipo de justificación de verdades proposicionales para determinar su naturaleza semántica y epistemológica. La propuesta de Carnap se caracteriza por hacer distinciones entre los tipos de enunciados de S en términos de sus compromisos lógicos y empíricos. En consecuencia, aquellos enunciados cuya naturaleza semántica y epistemológica puede conocerse tan sólo por condiciones sintácticas, o bien por aspectos semánticos-técnicos serán considerados analíticos y a priori, mientras aquellos enunciados de S no determinados sólo por la sintaxis o por las condiciones técnicas de la semántica, serán considerados sintéticos y a posteriori.

La exposición de (1935) tiene como antesala el sistema lógico-mátemático desarrollado por Russell y Whithead en Principia Mathematica (1910) y la Teoría de la Prueba desarrollada por Hilbert.¹⁰ Carnap, considera, por una parte, el papel que desempeña los constituyentes básicos de su teoría sintáctica: 'Sistema de reglas', 'Términos generales o sintácticos', 'L-Términos' y 'F-términos'. Por otra parte, establece el papel de tales constituyentes en la teoría así como sus distintas implicaciones. A partir del desarrollo de estos dos aspectos Carnap caracterizará sintácticamente a la analiticidad y sistematizará el conjunto de enunciados del lenguaje.

Por cuestiones de espacio no expondré aquí cada punto de la teoría sintáctica y me centraré en lo fundamental de ella para los propósitos de este artículo: la analiticidad. La sintaxis lógica consiste en dos partes básicas: i. el análisis de las reglas de formación de S (conjunto contable de símbolos como símbolos de S y un conjunto de expresiones de S llamadas "el conjunto de las fórmulas bien formadas"); ii. el análisis de las reglas de transformación de S (inferencia deductiva y un subconjunto de fórmulas bien formadas llamadas "axiomas de S"). (i) y (ii) implica privilegiar los términos de enunciado y consecuencia directa.

Los enunciados de S pueden ser verdaderos o falsos.¹¹ Los enunciados verdaderos a partir únicamente de la sintaxis serán enunciados válidos, mientras los falsos serán contraválidos. Un enunciado es válido, si es consecuencia de la clase vacía de premisas (Cfr. Carnap [1935] (1996): 48) en el marco de una prueba i.e. es un teorema derivado desde una cadena de consecuencias directas, la cual inicia con la clase vacía de premisas y finaliza con el enunciado probado. Ahora bien, en la prueba podemos distinguir dos tipos de enunciados válidos: i. axiomas (enunciados primitivos) y ii. teoremas (enunciados demostrados) (Cfr. Carnap [1935] (1996): 45 y 48-49). Por su parte, un enunciado ex. gr. A será contraválido, si todos los enunciados S son consecuencia de A. Esto es, todos los enunciados de la Principia Mathematica que no pueden ser probados ex. gr. "p & - p" o " - (p v p)". No probar A implica mostrar que un enunciado B, al igual que - B, son consecuencia de A; tal que, probar B y su negación implica considerar que cualquier enunciado pueda ser deducido. Por lo tanto, si B y - B son consecuencia de A, todo enunciado es consecuencia de A, luego A es contraválido. Adicionalmente, de acuerdo con Carnap, los enunciados sean éstos válidos o contraválidos serán considerados enunciados determinados en S, luego un enunciado será indeterminado si éste no es válido ni contraválido.¹² Los enunciados determinados son, entonces, aquellos para los que las reglas del lenguaje son suficientes para decidir su valor de verdad. En suma, loe enunciados válidos son deducibles en el sistema; los contraválidos son aquellos cuyas negaciones son deducibles en el sistema; y respecto a los indeterminados, ni ellos ni sus negaciones son deducibles en el sistema.

Ahora bien, cuando un lenguaje S contiene únicamente enunciados primitivos y reglas de inferencia de carácter estrictamente lógico, tales reglas, por su condición matemática prevaleciente, son llamadas por Carnap: 'L-reglas'. Si incluimos en S leyes físicas que funcionen como enunciados primitivos —ex. gr los principios de la mecánica de Newton, las ecuaciones de electromagnetismo de Maxwell, los principios de la termodinámica— tales reglas tienen un carácter extra-lógico. Carnap llama a este tipo de reglas: 'F-reglas' (Cfr. Carnap [1935] (1996): 50-51).

La distinción entre 'L-reglas' y 'F-reglas' es muy importante para dar cuenta de la caracterización sintáctica de la analiticidad. Un enunciado C (conclusión) es una consecuencia de la clase P de premisas si existe una cadena de enunciados construidas en función de las reglas de inferencia conectando a la clase P con el enunciado C. Si en la prueba únicamente se aplican 'L-reglas', entonces tal enunciado es una L-consecuencia de P. En un segundo caso, si C puede ser deducida a partir de P, sólo o con la participación de 'F-reglas' entonces C es una F-consecuencia de P . (Cfr. Carnap [1935] (1996): 52).

La inclusión de 'F-reglas' en conjunción con la noción de F-consecuencia nos permite comparar la noción de 'sinteticidad' y 'verdad a posteriori' en Frege con los resultados hasta ahora obtenidos por Carnap. De acuerdo con Frege y Carnap, si en la prueba de un enunciado C damos con enunciados (P1,.. .,Pn) que son de naturaleza no lógica y pertenecen a un campo científico distinto, entonces los enunciados (P1,.. .,Pn) serán para el primero enunciados sintéticos o bien verdades a posteriori, mientras para el segundo se tratará de casos de 'F-reglas' o F-consecuencias, respectivamente.

Finalmente, si un enunciado es verdadero en función únicamente de 'L-reglas' entonces tal enunciado al ser 'L-válido', será analítico: "por lo tanto llamaremos a un enunciado que es verdadero únicamente en virtud de las L- reglas, L-válido o analítico" (Carnap [1935] (1996): 53). Esta definición de analiticidad es entonces análoga a la definición de validez: un enunciado es analítico si éste ha sido probado —es consecuencia— a partir de la clase vacía de premisas i. e. se trata de una L-consecuencia de la clase vacía de premisas.¹³

Con base en los resultados obtenidos es posible enumerar caracterizaciones de los tipos de enunciados en S desde la sintaxis:

a. Un enunciado falso cuyo valor de verdad se sigue exclusivamente de 'L-reglas' es un enunciado L-contraválido o contradicción, i.e. A es un enunciado contradictorio si todo enunciado del lenguaje es una L-consecuencia de A.

b. Un enunciado es L-determinado si es ya analítico, ya contradictorio.

c. Si un enunciado no es L-determinado —i.e. la asignación de su valor de verdad no se sigue únicamente de 'L-reglas', tal enunciado es llamado L-indeterminado o sintético.

d. Los enunciados sintéticos, como hemos visto, son para Frege y Carnap aquellos afirman estados de cosas.

e. En suma, todos los enunciados 'L-válidos' son analíticos, i.e. lógicamente verdaderos o expresan una verdad necesaria. Por (a) todos los enunciados L-contraválidos serán contradictorios. Por (c) los enunciados indeterminados serán sintéticos.

Así, mientras Frege defiende una analiticidad de tipo lógico —deducción— y, de tipo semántico —decidibilidad del valor de verdad de los enunciados aritméticos—, Carnap (1935) explícitamente incluye en la definición de 'consecuencia lógica' el rasgo distintivo del predicado 'es analítico'. Incluye en la extensión de tal predicado el ejercicio deductivo y la asignación del valor de verdad a las fórmulas. De cualquier forma, tanto Frege como Carnap coinciden en la extensión del predicado: un enunciado es analítico si tiene la propiedad de ser consecuencia lógica de leyes lógicas generales y definiciones, o bien, es un axioma lógico.

Si consideramos ahora las observaciones semánticas de Carnap desde Meaning and Necessity (1947) veremos que el proyecto sintáctico y semántico se encuentran estrechamente vinculados. En ambos casos, los enunciados analíticos serán aquellos que expresan verdades necesarias o verdades lógicas. Particularmente, el programa semántico coincide con los puntos (b)¹⁴, (c)¹⁵ y ( e ) arriba señalados. De acuerdo con Carnap (1947) la verdad de un enunciado analítico se explica por medio del concepto 'L-verdad': "[n]uestro concepto de L-verdad ... pretende ser un explicatum para el concepto familiar pero vago de verdad lógica o verdad necesaria o verdad analítica el cual funciona como explicandum" (Carnap. 1947: 10) De tal suerte, si la verdad lógica de un enunciado se sigue de satisfacer la condición de derivarse de la clase vacía de premisas —sintaxis lógica—, entonces, tal consideración se encontraría en dificultades a partir de los resultados de Gõdel sobre la indecidibilidad de algunos sistemas formales matemáticos.¹⁶ Para tratar de evitar estos problemas técnicos, pero sobre todo para salvaguardar su explicación de la propiedad 'ser analítico' como el rasgo que dota a las verdades de los enunciados lógicos de un mayor grado de generalidad —a diferencia de las verdades no lógicas—, Carnap intenta identificar complementariamente los rasgos de la analiticidad en términos de descripciones de estado (state-description).

Las descripciones de estado se refieren a la clase de enunciados que contienen todos los enunciados atómicos, su verdad o su negación, pero no ambos, ni tampoco otro tipo de enunciados. Tal clase da una completa descripción de un estado posible del universo de individuos considerando todas las propiedades y relaciones expresadas por los predicados del sistema. En otras palabras, las descripciones de estado representan los mundos posibles de Leibniz o los estados de cosas posibles de Wittgenstein (Cfr. Carnap, 1947: 9). En este caso, un enunciado lógicamente verdadero, necesario o analítico lo es, en tanto su verdad se sostiene en todas las descripciones de estado posibles (Cfr. Carnap, 1947: 10). Bajo estas condiciones, el enunciado 'el predicado se aplica únicamente y a todos...' especifica el rango de aplicación y no aplicación del predicado 'es analítico' i.e. un tipo de explicatum del explicandum 'es analítico' incluye en su extensión el conjunto de enunciados a los que se aplica el predicado 'verdadero en todas las descripciones de estado posibles':

2-1. Convención. Un enunciado es L-verdadero en un sistema semántico S si y sólo si es verdadero en S en tal sentido en que su verdad pueda ser establecida sobre las bases de las reglas semánticas del sistema S únicamente, sin alguna referencia a hechos (extra-lingüísticos) (Carnap, 1947: 10).

La consideración anterior descansa en la definición: "2-2. Definición. Un enunciado 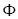es L-verdadero (en S₁) = df 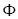_i se mantiene en toda descripción de estado (en S₁)" (Carnap, 1947: 10). Esta definición le sirve a Carnap para soportar la consideración semántica de arriba i .e. 'mantenerse en toda descripción de estado posible' es definida por las reglas semánticas de S₁. Así la analiticidad es un aspecto formal —o de interpretación semántica técnica— y no factual en cualquier caso. En palabras de Carnap:

¿Cómo debemos definir L-Verdad a fin de cumplir con el requerimiento de 2-1? Una forma sugerida por la concepción de Leibniz es que una verdad necesaria debe mantenerse en todos los mundos posibles, esto significa que una oración es lógicamente verdadera si ésta se mantiene en todas las descripciones de estado (Carnap, 1947: 10).

A partir de los resultados anteriores un enunciado es analítico si cumple la restricción: de acuerdo con las reglas semánticas de S un enunciado en el sistema de lenguaje S es L-verdadero, analítico o lógicamente necesario sii tal enunciado expresa una verdad en todas las descripciones de estado posibles, tal que cualquier enunciado matemático en S puede ser necesariamente verdadero en S sólo en función de las reglas semánticas de S, las cuales contienen y aplican el conjunto de descripciones de estado posibles.

De esta manera, Carnap desarrolla dos programas para atribuir la propiedad 'ser analítico' a los enunciados en un sistema de lenguaje y con ello justificar por qué se considera a los enunciados lógicos como aquellos que expresan verdades con mayor generalidad. En primer lugar, el predicado 'es verdadero' se explica en términos de la relación de consecuencia lógica (sintáctica), lo que hace de este desarrollo un acercamiento al predicado propiamente sintáctico. En segundo lugar, Carnap desarrolla un sistema semántico, el cual identifica los rasgos de la analiticidad en función del concepto semántico: descripciones de estado. Tal que, un enunciado es analítico sii no puede darse el caso que exprese una falsedad en alguna descripción de estado posible.

Por último, las dos propuestas de Carnap abren una discusión importante sobre la analiticidad y la aprioricidad. A la luz de los resultados de Gödel, en tanto a Carnap le interesaba explicar la extensión del predicado 'es analítico, este es un esfuerzo satisfecho en la estructura de una lógica proposicional de primer orden. Lo anterior implica que la propuesta sintáctica y semántica tenga la misma extensión: los enunciados L-verdaderos son verdaderos en todas las descripciones de estado posible y un enunciado es analítico si es consecuencia lógica del conjunto de premisas que no tiene miembros. Ambas consideraciones coinciden en el mismo rango lógico.

Claramente las aportaciones de los programas logicistas no tienen problema con el uso del predicado 'es analítico'. Al parecer, sus criterios formales —prueba: leyes lógicas generales, definiciones admisibles y consecuencia lógica— son suficientes para la clasificación y sistematización del conjunto de enunciados que ocurren en los lenguajes de primer orden. Sin embargo, aun cuando se trata de un trabajo técnico y convencional que ofrece una interpretación clara del predicado 'ser analítico', la extensión logicista de dicho predicado es claramente estrecha, pues la extensión del predicado se ha definido dentro de los límites de un contexto semántico-técnico que dice poco del uso de tal predicado en los contextos de los lenguajes naturales.

Considerando este último caso, una teoría semántica interesante para el lenguaje natural debe decirnos en qué sentido la explicación del concepto de la analiticidad implica la defensa de nuestra disposición por mantener ciertas verdades —expresadas por un tipo de enunciados— frente a cualquier cambio de hechos, en contextos técnicos y ordinarios. Este es el reto que enfrentan actualmente los programas semantistas-técnicos, semantistas-naturalizados, así como los programas naturalistas y metafísicos. Abordar al menos, algunas de estos casos, es una buena motivación para un siguiente artículo. Por ahora, se ha cumplido nuestro objetivo: ofrecer al lector en un sólo material útil, un análisis riguroso de las explicaciones logicistas paradigmáticas de la analiticidad que dan origen a las discusiones contemporáneas.

 

FUENTES CONSULTADAS

Boghossian, P., Peacocke, C. (eds.) (2000), New Essays on the A Priori, Oxford-Nueva York: Oxford University Press (OUP).         [ Links ]

Carnap, R. (1996) [1935], "Logical Syntax of Language", en Philosophy and Logical Syntax, Bristol, uk: Thoemmes [facsímil de la edición original publicada en Londres: Kegan Paul, Trench, Trubner & Co., 100 pp.         [ Links ]].

---------- (1967) [1934], Logical Syntax of Language, Londres: Routledge & Kegan Paul [versión original: Logische Syntax der Sprache, Viena, ulius Springer]         [ Links ].

---------- (1947), Meaning and Necessity: A Study in Semantics and Modal Logic, Chicago: University of Chicago Press.         [ Links ]

Frege, G. (1986) [1884], Die Grundlagen der Arithmetik. Eine logisch mathematische Untersuchung über den Begriff der Zahl, Centenar Ausgabe, Christian Thiel (ed.), Hamburgo: Felix Meiner [edición original en Breslau: Wilhelm Koebner]         [ Links ].

---------- (1972a) [1879], "Conceptografía", en Conceptografía. Los fundamentos de la aritmética. Otros estudios filosóficos, México: Instituto de Investigaciones Filosóficas (IIF)-UNAM.         [ Links ]

---------- (1972b) [1884], "Los fundamentos de la aritmética", en Conceptografía. Los fundamentos de la aritmética. Otros estudios filosóficos, México: Instituto de Investigaciones Filosóficas (IIF)-UNAM.         [ Links ]

Gödel, K. (1986) [1931], "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme i" ("On formally undecidable propositions of Principia mathematica and related Systems i"), versión bilingüe en Solomon Feferman (ed.), Kurt Gödel. Collected Works, vol. i: Publications 1929-1936, Nueva York: OUP, pp. 144-195.         [ Links ]

Hilbert, D. (1931), "Die Grundlegung der Elementaren Zahlenlehre", en Mathematische Annalen, vol. 104, Berlín-Heidelberg: Springer, pp. 485-494 [versión en inglés: "The Grounding of Elementary Number Theory", en Paolo Mancosu (ed.) (1998), From Brouwer to Hilbert: The Debate on the Foundations of Mathematics in the 1920's, Nueva York: Oxford University Press, pp. 266-273]         [ Links ].

Hintikka, J. (2009), "Logicism" en Andrew D. Irvine (ed.), Handbook of the Philosophy of Mathematics, Amsterdam: Elsevier, pp. 271-290.         [ Links ]

Horwich, P. (2000), "Stipulation, Meaning, and Apriority", en Paul Boghossian y Christopher Peacocke (eds.), New Essays on the A Priori, Oxford-Nueva York: OUP, pp. 150-169.         [ Links ]

Kant, I. (1978), Crítica de la razón pura, 3a ed., Madrid: Alfaguara.         [ Links ]

Kitcher, P. (2000), "A priori Knowledge Reviseted", en Paul Boghossian y Christopher Peacocke (eds.), New Essays on the A Priori, Oxford-Nueva York: OUP, pp. 65-91.         [ Links ]

---------- (1980), "Apriority and Necessity", en Australiasan Journal of Philosophy, vol. 58, num. 2, junio, Tasmania, AU/Londres: The Australasian Association of Philosophy/Routledge, pp. 89-101.         [ Links ]

Kripke, S. (1980) [1972], Naming and necessity, Cambridge, Massachusetts, Oxford: Harvard University Press [originalmente publicado en Donald Davidson y Gilbert Harman, (eds.), Semantics of Natural Language, Dordrecht, HOL-Boston, MA: Dordrecht Reidel, pp. 253-355]         [ Links ].

Morado, R. (1987), "Frege, Hempel and Dedekin: Definition of Number and Correferentiality", en Ergo, vol. i, num. 2, agosto, Xalapa: Facultad de Filosofía y Letras-Universidad Veracruzana, pp. 45-56.         [ Links ]

Quine, W. O. (1951), "Two Dogmas of Empiricism", en The Philosophical Review, vol. 60, num. 1, enero-marzo, pp. 20-43 [versión castellana: "Dos dogmas del empirismo", en Willard van Orman Quine, Desde un punto de vista lógico, 2a ed., Barcelona, Paidós, 2002, pp. 61-91]         [ Links ].

Russell, B. (1983) [1919], "Mathematics and Logic", en Paul Benacerraff e Hilary Putnam (eds.), Philosophy of Mathematics. Selected Readings, 2a ed., Cambridge, UK: Cambridge University Press (CUP), pp. 173-182 [publicado originalmente como el capítulo XVIII de Bertrand Russell, Introduction to Mathematical Philosophy, Londres-Nueva York: George Allen & Unwin/The Macmillan Co., pp. 194-206]         [ Links ].

Russell, B., Whitehead, A. N. (1910-1913), Principia Mathematica, 3 vols., Cambridge-Londres: CUP.         [ Links ]

Tarski, A. (1956) [1936], "On the Concept of Logical Consequence", en Logic, Semantics, Metamathematics. Papers from 1923 to 1938, Oxford: Clarendon Press, pp. 409-420 [apareció originalmente en polaco como "O pojciu wynikania logicz-nego", en Przeglad Filozoficzny, vol. 89, 1936, pp. 58-68 y en alemán con el título "Úber den Begriff der logischen Folgerung", en Actes du Congrès International de Philosophie Scientifique, vol. 7, París, Actualités Scientifiques et Industrielles, 1936, pp. 1-11]         [ Links ].

---------- (1994) [1941], Introduction to Logic and to the Methodology of Deductive Sciences, 4a ed., edición preparada por Jan Tarski, Nueva York-Oxford: oup [traducción inglesa que expande y actualiza la version original en alemán: Einfürung in die matematische Logik un in die Methodologie der Mathematik, Viena: Julius Springer]         [ Links ].

 

Notas

¹ Como indiqué al inicio de este artículo existen distintos planteamientos más contemporáneos, los cuales enfrentan el problema de caracterizar las nociones de analiticidad, aprioricidad y necesidad, a partir del debate abierto por los logicistas, ex. gr. Paul Boghossian (2000), Cristopher Peacocke (2000), Philip Kitcher (1980) y (2000), Paul Horwich (2000), sólo por mencionar algunos casos. Las referencias completas de estos casos se encuentran en la sección Bibliografía.

² Con 'reducción conceptual' me refiero a la motivación logicista por definir todo concepto matemático en términos estrictamente lógicos i.e. cada concepto matemático puede reducirse en términos exclusivamente lógicos.

³ Con 'decidibilidad' me refiero a la creencia logicista de obtener cualquier verdad matemática mediante un mecanismo finito de prueba estrictamente lógico i.e. toda verdad matemática puede ser probada —deducirse— mediante axiomas lógicos, leyes lógicas generales y definiciones lógicas, exclusivamente.

⁴ Siguiendo los lineamientos editoriales de Andamios no incluyo en ningún caso las citas de autores en su idioma original (inglés y alemán), considerando que es posible incluir una traducción estándar en español. Particularmente, las citas en español incluidas en éste trabajo de Hintikka (2009), Morado (1987) y Carnap ([1935] (1996) y (1947)) son responsabilidad mía. De cualquier forma, las referencias en el cuerpo del texto corresponden a las referencias originales.

En este caso, pongo en negritas algunas expresiones de la consideración de Hintikka. La finalidad de esta distinción es notar cómo con este autor podemos identificar también los dos aspectos que caracterizan a la tesis reduccionista del logicismo: reducción entre términos y reducción por prueba (teoremas).

⁵ "En todos los juicios en los que se piensa la relación entre un sujeto y un predicado (me refiero solo a los afirmativos), ...el predicado B pertenece al sujeto A como algo que está (implícitamente ) contenido en el concepto A...Si digo por ejemplo: " Todos los cuerpos son extensos" tenemos un juicio analítico...no tengo necesidad de ir más allá del concepto que ligo "cuerpo" para encontrar la extensión como enlazada con él. Cfr. Kant, I., (1984) Crítica de la Razón Pura, México, D.F.: Alfaguara, pp. 47-48.

⁶ Uso 'AF" para nombrar: Analiticidad fregeana.

⁷ La noción de consecuencia lógica en un principio es un concepto primitivo. Este se usa para afirmar simplemente ex. gr. que A se sigue de B. Esta noción debe distinguirse del concepto derivabilidad. La derivabilidad es un concepto que se empieza a utilizar de manera rígida en los sistemas de la lógica. Se pensaba que tal concepto capturaba la noción intuitiva de consecuencia lógica. Sin embargo, actualmente el uso de esta última noción se ha modificado. A partir de Tarski la consecuencia lógica tiene un sentido teórico: A es consecuencia lógica de B si y sólo si toda estructura semántica que es un modelo de B es un modelo de A. Estas distinciones entre consecuencia lógica como idea intuitiva, la derivabilidad como concepto que captura la idea intuitiva de consecuencia lógica y la consecuencia lógica como noción teórica puede rastrearse ya en los trabajos de Carnap (1935) y (1947), aún cuando es hasta Tarski que se establecen explícitamente estas diferencias. De tal suerte, cuando decimos que para Frege un enunciado es analítico sii es consecuencia lógica de leyes lógicas generales y definiciones, y de acuerdo con Carnap, un enunciado es analítico sii es consecuencia lógica de la clase vacía de premisas, expresamos —en ambos casos— la propiedad que tiene un enunciado de derivarse lógicamente de estas condiciones, donde la derivabilidad debe entenderse como el concepto que captura la idea intuitiva de consecuencia lógica.

⁸ De acuerdo con Frege en su Begriffsschrift (1879) la investigación lógica es lo que actualmente llamamos semántica: una doctrina del contenido, una investigación sobre la naturaleza y estructura del significado. Sin embargo, Frege distinguió sus propias concepciones de Lógica y, aun cuando lo anterior es correcto, en Die Grundlagen der Arithmetik Frege tiene como uno de sus objetivos principales aislar el carácter lógico del lenguaje, separar los rasgos psicológicos de los lógicos y a partir de esto caracterizar el lenguaje de las matemáticas, en principio su condición analítica. Además no debemos olvidar que el objetivo principal de los Grundlagen, es mostrar que todos los cimientos de la matemática están basados en leyes generales de la lógica.

⁹ En este caso, la prueba lógica funciona como la evidencia de las verdades aritméticas, así como los hechos empíricos pueden funcionar como evidencia de las verdades físicas.

¹⁰ La teoría de la prueba o la demostración de David Hilbert fue desarrollada en la década de los 1920. Por ejemplo, Cfr. Hilbert, D. "Die Grundlagen Der Elementaren Zahlentheorie" en Mathematische Annalen 04, pp. 485-94. Versión en Inglés, Mancosu (edit) (1998), "The Grounding of Elementary Number Theory" en From Brouwer to Hilbert: The debate on the foundations of mathematics in the 1920s, New York: Oxford University Press, pp. 266-273.

¹¹ Carnap (1935) considera el caso de enunciados verdaderos o falsos en función únicamente de las reglas sintácticas del lenguaje sin considerar aspectos extralingüísticos.

¹² Si un enunciado es indeterminado (no es posible decidir su valor de verdad sólo por la sintaxis), entonces estará construido mediante la introducción de variables no lógicas. De acuerdo con Carnap, éstos lógicamente indeterminados constituirán al conjunto de enunciados sintéticos.

¹³ Técnicamente la consecuencia lógica —en Carnap— se expresa de la siguiente manera:

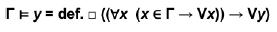
y es consecuencia lógica del conjunto de premisas (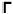) si y solo si por definición es necesario (□) que si para todo enunciado X que pertenezca a gama, X es verdadera, entonces Y es también verdadera.

Carnap identifica la condición 'ser consecuencia de la clase vacía de premisas' como el explicatum del explicandum 'ser analítico', tal que la extensión de ser consecuencia de la clase vacía de premisas es la extensión de 'ser analítico' y, la satisfacción de tal condición a su vez permite establecer el tipo de verdad que expresa tal tipo de enunciado. De tal suerte, de acuerdo con Carnap (1935), la verdad que expresa un enunciado analítico será a priori mientras la naturaleza de la verdad que contienen otros tipos de enunciados será, en principio, no a priori. Es importante mencionar que el explicatum del explicandum 'ser analítico' sólo es correcto dentro de una interpretación estándar de las contantes lógicas. Recordemos que Carnap utiliza indistintamente los predicados 'ser analítico', 'ser verdadero lógicamente' y 'ser necesario'.

¹⁴ "2. Conceptos-L. ...Un enunciado es llamado L-determinado si este es tanto L-verdadero o L-Falso" (Carnap, 1947: 7).

¹⁵ "2. Conceptos-L...L-indeterminado o factual. El último concepto es un explicatum para lo que Kant denominó juicio sintético" (Carnap, 1947: 7).

¹⁶ De acuerdo con Gödel, no hay un sistema adecuado para formalizar la aritmética de manera recursiva, mucho menos sistemas inclusivos que puedan ser completos en función de algún procedimiento de derivación formal (Cfr. Gödel, [1931] (1986), "Über formal unentscheidbare Sätze der Principia mathematica und verwandter Systeme I' en S. Feferman (et al.) (edit.), Kurt Godel. Collected Works. Volume I: Publications 1929-1936, New York: Oxford University Press, 1986, pp. 116-195.). Estas consecuencias representan una auténtica crítica a los planteamientos de Carnap en la medida en que éste último, sí propone —como hemos visto— un procedimiento formal para sistematizar tanto el tipo de enunciados matemáticos en particular, como los de la ciencia empírica en general, de acuerdo con las condiciones que se establecen en su sintaxis lógica. Así, las relaciones de consecuencia lógica como derivabilidad son insuficientes para probar que todos los enunciados matemáticos o su negación se siguen de las restricciones del explicatum de 'ser analítico': seguirse de la clase vacía de premisas.

 

INFORMACIÓN SOBRE EL AUTOR:

Jesús Jasso Méndez. Doctor en Filosofía de la Ciencia en la línea terminal Filosofía de las Matemáticas y Lógica de la Ciencia, UNAM, México. Forma parte del grupo de investigación Logic, Language and Cognition Research Group (LOGOS), UB, Barcelona, España. Es profesor-investigador de la Academia de Filosofía e Historia de las Ideas en la Universidad Autónoma de la Ciudad de México (UACM). sus temáticas de investigación son: Filosofía del Lenguaje, Estructuralismo en Filosofía de las Matemáticas, Lógica, Epistemología, Argumentación, Lógica Informal y Pensamiento crítico. Dirección electrónica: jess.jasso@gmail.com