Artículos

 

Modelado para vigas de sección transversal "I" sometidas a una carga uniformemente distribuida con cartelas rectas

 

Arnulfo Luévanos Rojas

 

Facultad de Ingeniería, Ciencias y Arquitectura Universidad Juárez del Estado de Durango Av. Universidad S/N, Fracc. Filadelfia, CP 35010, Gómez Palacio, Durango, México. Correo electrónico: arnulfol_2007@hotmail.com

 

Fecha de recepción: 25-09-2014.
Fecha de aceptación: 18-12-2014.

 

Resumen

Este documento presenta un modelo matemático para vigas de sección transversal "I" con cartelas rectas para el caso general (simétricas y/o no simétricas) sujetas a una carga uniformemente distribuida tomando en cuenta las deformaciones por flexión y cortante para obtener los momentos de empotramiento, factores de transporte y factores de rigidez, que es la novedad de esta investigación. Las propiedades de la sección transversal de la viga varían a lo largo de su eje "x", es decir, el ancho del patín "b", el espesor del patín "t", el espesor del alma "e" son constantes y la altura del alma "d" es variable a lo largo de la viga, esta variación es de tipo lineal. El método de deformación consistente se utiliza para resolver este tipo de problemas, y las deformaciones en cualquier parte de la viga se encuentran por el método de la viga conjugada mediante la integración exacta usando el software "Derive" para obtener algunos resultados. Los modelos tradicionales consideran únicamente las deformaciones por flexión y otros autores presentan tablas considerando las deformaciones por flexión y cortante, pero están limitadas. También una comparación se realiza entre el modelo tradicional y el modelo propuesto para observar las diferencias. Además de la eficacia y la precisión del modelo desarrollado, una ventaja significativa es que los momentos de empotramiento, factores de transporte y factores de rigidez se calculan para cualquier sección transversal "I" de la viga usando las fórmulas matemáticas.

Palabras clave: vigas de sección transversal "I", carga uniformemente distribuida, cartelas rectas, momentos de empotramiento, factores de transporte, factores de rigidez.

 

Abstract

This paper presents a mathematical model for beams of cross section "I" with straight haunches for the general case (symmetrical and/or non-symmetrical) subjected to a uniformly distributed load taking into account the bending deformations and shear to obtain the fixed-end moments, carry-over factors and stiffness factors, which is the novelty of this research. The properties of the cross section of the beam vary along its axis "x", i.e., the flange width "b", the flange thickness "t", the web thickness "e" are constant and the height "d" varies along the beam, this variation is linear type. The consistent deformation method is used to solve such problems, and the deformations anywhere of beam are found by the conjugate beam method through exact integrations using the software "Derive" to obtain some results. The traditional model takes into account only bending deformations, and others authors present tables considering the bending deformations y shear, but are restricted. Besides the effectiveness and accuracy of the developed models, a significant advantage is that fixed-end moments, carry-over factors and stiffness factors are calculated for any cross section of the beam "I" using the mathematical formulas.

Keywords: beams of cross section "I", uniformly distributed load, straight haunches, fixed-end moments, carry-over factors, stiffness factors.

 

Introducción

En la ingeniería estructural exciten circunstancias, donde las vigas son no uniformes, en el sentido de que la geometría y/o las propiedades del material varían a lo largo de la longitud. Por ejemplo, los miembros estructurales no prismáticos con cartelas escalonadas, rectas o parabólicas, que se aplican comúnmente en el diseño de ingeniería para reducir el peso y optimizar la fuerza y la estabilidad o para cumplir los requisitos arquitectónicos y funcionales específicos.

Uno de los principales problemas en el análisis de estructuras con momento de inercia variable a lo largo de su longitud es encontrar los momentos de empotramiento, rigideces y factores de transporte.

Durante el siglo pasado, entre 1950 y 1960 se desarrollaron varias ayudas de diseño, como las presentadas por Guldan [1]. Las tablas publicadas por la Portland Cement Association (PCA) en 1958, donde se presentan constantes de rigideces y momentos de empotramiento para miembros de sección variable, las hipótesis utilizada son: 1) La variación de la rigidez de las cartelas (lineal o parabólica, según sea el caso de la geometría) se consideran en función del momento de inercia principal en flexión; 2) Las deformaciones por cortante se despreciaron; 3) La relación claro-peralte de la viga en la definición de los diversos factores de rigidez se despreciaron [2-3],

La formulación elástica de la rigidez de miembros de sección variable fue evolucionado con el tiempo, y posteriores a la publicación de las tablas de la PCA, los siguientes trabajos merecen mención especial todos ellos se basan en la teoría de vigas: Just fue el primero en proponer la formulación de la flexión y matrices de rigidez axial para las vigas de sección variable de secciones transversales cajón e I [4]. Schreyer desarrolló una teoría vigas para los miembros linealmente cónicos para tener en cuenta las deformaciones por cortante, con el uso de una hipótesis Kirchhoff generalizada en la que se supone que las deformaciones de corte transversal en coordenadas cilindricas debe ser cero [5]. Medwadowski presenta una solución del problema de la flexión de vigas no prismáticas, incluyendo el efecto de las deformaciones de cortante utilizando la teoría del cálculo de variaciones [6]. Brown propuso un método para encontrar una matriz de rigidez a la flexión modificada para vigas de sección variable [7].

Las matrices de rigidez elástica para miembros bidimensionales y tridimensionales de elementos de sección variable basado en la teoría clásica de vigas de Bernoulli-Euler y el método de las flexibilidades tomando en cuenta las deformaciones axiales y cortante, así como la forma de la sección transversal se encuentran Tena Colunga y Zaldo [8], y en el apéndice B [9]. Pero las tablas se limitan a ciertas relaciones. Artículos publicados recientemente son: Shooshtari y Khajavi propusieron las funciones de forma y matrices de rigidez de los elementos de viga no prismáticas para las formulaciones de Euler-Bernoulli y Timoshenko [10]. Yuksel realizó un estudio para investigar el comportamiento de vigas no prismáticas con cartelas parabólicas simétricas que tienen la relación longitud de cartela constante de 0.5 utilizando análisis de elementos finitos debido a cargas verticales, para obtener los coeficientes de rigidez y de los factores de transporte [11]. Luévanos Rojas propuso un modelo matemático para vigas rectangulares de sección transversal variable de forma parabólica simétrica para carga distribuida uniformemente [12]. Luévanos Rojas y Montoya Ramírez presentaron un modelo matemático para vigas rectangulares de sección transversal variable de forma lineal simétrica para carga distribuida uniformemente [13]. Luévanos Rojas et al. propusieron un modelo matemático para vigas rectangulares de sección transversal variable de forma lineal simétrica para carga concentrada [14],

Los métodos tradicionales que se han utilizado para miembros de sección variable para calcular las deflexiones se requiere de la solución de una integral, en donde el momento de inercia, la geometría y carga del miembro se exprese como función de la coordenada "x" de la longitud, estas deflexiones son obtenidas por medio de la regla de Simpson o alguna otra técnica numérica para llevar a cabo la integración [15-17], y otros autores presentan tablas considerando las deformaciones por flexión y cortante, pero están limitadas para ciertas relaciones [9],

Este documento presenta un modelo matemático para vigas de sección transversal "I" con cartelas rectas para el caso general (simétricas y/o no simétricas) sujetas a una carga uniformemente distribuida tomando en cuenta las deformaciones por flexión y cortante para obtener los momentos de empotramiento, factores de transporte y factores de rigidez, que es la novedad de esta investigación. Las propiedades de la sección transversal de la viga varían a lo largo de su eje "x", es decir, el ancho del patín "b", el espesor del patín "t", el espesor del alma "e" son constantes y la altura del alma "d" es variable a lo largo de la viga, esta variación es de tipo lineal. El método de deformación consistente se utiliza para resolver este tipo de problemas, y las deformaciones en cualquier parte de la viga se encuentran por el método de la viga conjugada mediante la integración exacta usando el software "Derive" para obtener algunos resultados. También una comparación se realiza entre el modelo tradicional y el modelo propuesto para observar las diferencias.

 

Modelo Matemático

Principios generales

En la Fig. 1 se muestra una viga en elevación y también se presenta su sección transversal "I" tomando en cuenta el ancho del patín "b", el espesor del patín "t" y el espesor del alma "e" constantes, y variando la altura del alma "d " de forma lineal en tres tramos diferentes.

El momento de inercia alrededor del eje Z "I_z" y el área de cortante "A_cx " a una distancia "x" son:

La altura del alma "d_y" varía con respecto a "x", se obtiene como sigue:

Sustituyendo las ecuaciones (4), (5) y (6) en la ecuación (1) para encontrar el momento de inercia "I_z" en los tres intervalos:

Sustituyendo las ecuaciones (4), (5) y (6) en la ecuación (2) para obtener el área de cortante "A_cx" generalizada para los tres intervalos:

 

Momentos de empotramiento para carga uniformemente distribuida

En la Fig. 2(a) se presenta la viga "AB" sujeta a una carga uniformemente distribuida y empotrada en sus extremos. Los momentos de empotramiento en sus extremos se encuentran mediante la suma de los efectos. Los momentos se consideran positivos, cuando giran en contra de las manecillas del reloj y negativo cuando giran a favor. En la Fig. 2(b) se observa la misma viga simplemente apoyada en sus extremos bajo la carga aplicada para encontrar las rotaciones "θ_A1" y "θ_B1". Ahora, las rotaciones "θ_A2" y "θ_B2" son causados por el momento "M_AB" aplicado en el soporte "A", según la Fig. 2(c), y en cuanto a "θ_A3" y "θ_B3" son causados por el momento "M_BA" aplicado en el soporte "B", esto se observan en la Fig. 2(d) [18-20].

Las condiciones de geometría son [18-23]:

La viga de la Fig. 2(b) es analizada para encontrar "θ_A1 y "θ_B1", el método de la viga conjugada se utiliza para obtener las rotaciones y teniendo en cuenta las deformaciones de flexión y cortante se calculan [9].

El valor de "θ_B1" para miembros no prismáticos se obtiene:

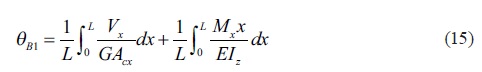
Ahora el valor de "θ_A1"para los miembros no prismáticos se encuentra:

donde: G es el módulo de cortante, E es el módulo de elasticidad, V_x es la fuerza cortante y M_x es el momento flexionante a una distancia "x".

La fuerza cortante en cualquier lugar de la viga sobre el eje "x" es [24]:

El momento en cualquier punto de la viga sobre el eje "x" es:

El módulo de cortante es:

donde v es la relación de Poisson.

Utilizando las ecuaciones (15) y (16) para obtener los valores de "θ_B1" y "θ_A1":

La viga de la Fig. 2(c) se analiza para encontrar "θ_A2" y "θ_B2" en función de "M_AB":

La fuerza cortante en cualquier lugar de la viga sobre el eje "x" es [24]:

El momento en cualquier punto de la viga sobre el eje "x" es

Empleando las ecuaciones (15) y (16) para encontrar "θ_B2" y "θ_A2"

Subsecuentemente, el miembro de la Fig. 2(d) es analizado para obtener "θ_A3" y "θ_B3" en función de "M_BA":

La fuerza cortante en cualquier lugar de la viga sobre el eje "x" es [24]:

El momento en cualquier punto de la viga sobre el eje "x" es:

Utilizando las ecuaciones (15) y (16) para obtener "θ_B3" y "θ_A3":

Las ecuaciones (21), (25) y (29) correspondientes al apoyo "A" se sustituyen en la ecuación (13), y las ecuaciones (20), (24) y (28) correspondientes al apoyo "B" se sustituyen en la ecuación (14). Subsecuentemente, las ecuaciones generadas se resuelven para obtener los valores de "M_AB" y "M_BA". Estas se presentan en las ecuaciones (30) y (31) del apéndice.

 

Factor de transporte y rigidez

El factor de transporte y rigidez se obtiene tomando en cuenta el siguiente problema: Si un momento en sentido de las manecillas del reloj "M_AB" se aplica en el apoyo simple de un miembro recto de sección transversal variable, simplemente apoyado en un extremo y empotrado en el otro, encontrar la rotación "θ_A" en el apoyo simple y el momento "M_BA" en el extremo empotrado, como se muestra en la Fig. 3.

Los momentos finales adicionales de "M_AB" y "M_BA", deben ser tales que causan rotaciones de "θ_A" y "θ_B", respectivamente. Si "θ_A2" y "θ_B2" son las rotaciones causados por "M_AB" de acuerdo con la Fig. 3(b), así como "θ_A3" y "θ_B3" son debidos a "M_BA", que se observa en la Fig. 3(c).

Las condiciones requeridas de geometría son [25]:

La viga de la Fig. 3(b) se analiza para obtener "θ_A2" y "θ_B2" en función de "M_AB" estos se muestran en las ecuaciones (24) y (25). La viga de la Fig. 3(c) se analiza para encontrar "θ_A3" y "θ_A3" en función de "M_BA", estos se presentan en las ecuaciones (28) y (29).

Ahora, las ecuaciones (24) y (28) se sustituyen en la ecuación (33). Posteriormente, se usan para obtener "M_BA" en función de "M_AB".

Por lo tanto, el factor de transporte de "A" a "B" es la relación del momento inducido en el apoyo "B" debido al momento aplicado en el apoyo "A", este es el coeficiente del momento "M_AB" expresado en la ecuación (34), se presenta en el apéndice.

Ahora, las ecuaciones (25) y (29) se sustituyen en la ecuación (32) y enseguida, la ecuación (34) se sustituye en esta ecuación para obtener "M_AB" en función de "θ_A". Entonces, el factor rigidez es el momento aplicado en el soporte "A" para causar una rotación de 1 radian en el soporte "A" es el coeficiente de la rotación "θ_A" expresado en la Ecuación (35), se presenta en el apéndice.

Ahora el procedimiento se usa para obtener el factor de transporte "B" a "A" presentado en la ecuación (36) y el factor de rigidez en el soporte "B" mostrado en la ecuación (37), estas ecuaciones se presentan en el apéndice.

 

Resultados

Las Tablas 1 y 2 muestran la comparación entre los dos modelos, el modelo propuesto (MP) es el modelo matemático presentado en este documento, donde las deformaciones por flexión y cortante se consideran, y el modelo tradicional (MT) toma en cuenta solo las deformaciones por flexión. Las Tablas presentan los factores de los momentos de empotramiento (m_AB y m_BA) para una viga sometida a una carga uniformemente distribuida, los factores de transporte (C_AB y C_BA), y los factores de rigidez (k_AB y k_BA). La Tabla 1 para L = 20d → d = 0.05L. La Tabla 2 para L = 10d → d = 0.10L. Dichas comparaciones se realizaron para v = 0.30 (acero estructural), b = 13.02t → t = 0.0768b, d = 26.91e → e = 0.0372d, b = 0.813d, u = f, porque estos valores se presentan en las Tablas del apéndice B por Tena Colunga [9]. Los resultados mostrados en la Tabla 1 mencionadas anteriormente son idénticos para el modelo propuesto.

Otra manera para validar el modelo propuesto es como sigue: sustituyendo "a = 0L" y "c = 0L" en la ecuación (30) y (31) para encontrar los momentos de empotramiento "M_AB = M_BA = wL²/12". Ahora, cuando "a = 0L" y "c = 0L" se sustituyen en la ecuación (34) y (36), y las deformaciones por cortante se desprecian para obtener los factores de transporte "C_AB = C_BA = 0.5". También en la ecuación (35) y (37) se sustituye "a = 0L" y "c = 0L", y también las deformaciones por cortante se desprecian para encontrar los factores de rigidez k_AB = k_BA = 4, por lo tanto la rigidez es "K_AB = K_BA = 4EI_z2/L". Los valores presentados anteriormente corresponden a una sección transversal constante.

Entonces el modelo propuesto en este documento es válido y no se limita para ciertas dimensiones o proporciones como algunos autores muestran, y también las deformaciones por flexión y cortante son consideradas.

La Tabla 1 muestra los momentos de empotramiento, los factores de transporte y los factores de rigideces de los miembros entre ambos modelos para d = 0.05L, la Tabla 2 para la relación d = 0.1L. De acuerdo con los resultados, las diferencias más grandes se presentan en la relación d = 0.1L. Cuando el momento de empotramiento de un miembro en un soporte es mayor con respecto al otro apoyo, en un apoyo el modelo tradicional es mayor, y en el otro apoyo es mayor el modelo propuesto, siendo la diferencia hasta de un 3.7%. En los factores de transporte el modelo tradicional es mayor en todos los casos y alcanza una diferencia hasta un 29.5%. En cuanto a los factores de rigideces el modelo tradicional también es mayor en todos los casos, siendo su diferencia hasta de un 61.4%.

 

Conclusiones

Este documento presenta un modelo matemático para vigas de sección transversal "I" con cartelas rectas para el caso general (simétricas y/o no simétricas) sujetas a una carga uniformemente distribuida tomando en cuenta las deformaciones por flexión y cortante para obtener los momentos de empotramiento, factores de transporte y factores de rigidez, que es la novedad de esta investigación. Las propiedades de la sección transversal de la viga varían a lo largo de su eje "x", es decir, el ancho del patín "b", el espesor del patín "t", el espesor del alma "e" son constantes y la altura del alma "d" es variable a lo largo de la viga, esta variación es de tipo lineal. Los modelos tradicionales consideran únicamente las deformaciones por flexión y otros autores presentan tablas considerando las deformaciones por flexión y cortante, pero están limitadas, por ejemplo L = 20d → d = 0.05L, v = 0.30 (acero estructural), b = 13.02t → t = 0.0768b, d = 26.91e → e = 0.0372d, b = 0.813d, u = f, esta relación se presenta en las Tablas por Tena Colunga [9].

Además de la eficacia y la precisión del modelo desarrollado en la presente investigación, una ventaja significativa es que puede aplicarse para cualquier sección transversal del tipo "I" de acero estructural como pueden ser los perfiles W, M, HP mediante la adaptación del perfil del intervalo central, donde la sección es constante y se hace un corte a la altura de la parte media del alma en el sentido longitudinal hasta donde empiezan las cartelas y se inserta una placa triangular del mismo espesor del alma para obtener la altura de las cartelas), y su principal aplicación es para los perfiles formados por tres placas soldadas, además también puede aplicarse para vigas de concreto reforzado o preesforzado del tipo "I" como puede observarse en puentes de grandes claros.

En cualquier tipo de estructura las fuerzas cortantes y los momentos flexionantes están presentes; por lo tanto, aparecen las deformaciones de flexión y cortante. Entonces, el modelo propuesto que considera las deformaciones por flexión y cortante es más apropiado para el análisis estructural y también se ajusta más a las condiciones reales con respecto al modelo tradicional que toma en cuenta las deformaciones por flexión únicamente.

La aplicación significativa de los momentos de empotramiento y las rigideces de un miembro es en los métodos matriciales de análisis estructural. Los momentos de empotramiento, el factor de transporte y el factor rigidez se utiliza en el método de distribución de momentos.

Las sugerencias para investigaciones futuras: 1) Cuando el miembro presenta otro tipo de sección transversal, por ejemplo sección transversal variable de tipo cajón, o "T"; 2) Cuando el miembro tiene otro tipo de configuración, por ejemplo cartelas parabólicas; 3) Cuando el miembro está sujeto a otro tipo de carga.

 

Referencias

[1] R. Guldan, Estructuras aporticadas y vigas continuas, El ateneo, Buenos Aires, 1956.         [ Links ]

[2] Portland Cement Association, Handbook of frame constants: Beam factors and moment coefficients for members of variable section, 1958.         [ Links ]

[3] A. Tena Colunga, Stiffness formulation for nonprismatic beam elements, Journal of Structural Engineering ASCE 122 (1996) 1484-1489.         [ Links ]

[4] D.J. Just, Plane frameworks of tapering box and I-section, Journal of Structural Engineering ASCE 103 (1977) 71-86.         [ Links ]

[5] H.L. Schreyer, Elementary theory for linearly tapered beams, Journal of Structural Engineering ASCE 104 (1978) 515-527.         [ Links ]

[6] S.J. Medwadowski, Nonprismatic shear beams, Journal of Structural Engineering ASCE 110 (1984) 1067-1082.         [ Links ]

[7] C.J. Brown, Approximate stiffness matrix for tapered beams, Journal of Structural Engineering ASCE 110 (1984) 3050-3055.         [ Links ]

[8] A. Tena Colunga, A. Zaldo, Ductilidad de marcos con trabes acarteladas y columnas de sección variable, Reporte FJBS/CIS-94/04, Centro de Investigación Sísmica, AC, Fundación Javier Barrios Sierra, 1994.         [ Links ]

[9] A. Tena Colunga, Análisis de estructuras con métodos matriciales, Limusa, México, 2007.         [ Links ]

[10] A. Shooshtari, R. Khajavi, An efficient procedure to find shape functions and stiffness matrices of nonprismatic Euler-Bernoulli and Timoshenko beam elements, European Journal of Mechanics - A/Solids 29 (2010) 826-836.         [ Links ]

[11] S.B. Yuksel, Assessment of non-prismatic beams having symmetrical parabolic haunches with constant haunch length ratio of 0.5, Structural Engineering and Mechanics 42 (2012) 849-866.         [ Links ]

[12] A. Luévanos Rojas, A Mathematical Model for Rectangular Beams of Variable Cross Section of Symmetrical Parabolic Shape for Uniformly Distributed Load, Far East Journal of Mathematical Sciences 80 (2013) 197-230.         [ Links ]

[13] A. Luévanos Rojas, J. Montoya Ramirez, Mathematical Model for Rectangular Beams of Variable Cross Section of Symmetrical Linear Shape for Uniformly Distributed Load, International Journal of Innovative Computing, Information and Control, 10 (2014) 545-564.         [ Links ]

[14] A. Luévanos Rojas, R. Luévanos Rojas, I. Luévanos Soto, R.G. Luévanos Vazquez, OA. Ramírez Luévanos, Mathematical Model for Rectangular Beams of Variable Cross Section of Symmetrical Linear Shape for Concentrated Load, International Journal of Innovative Computing, Information and Control 10 (2014) 851-881.         [ Links ]

[15] R.C. Hibbeler, Structural analysis, Prentice-Hall, Inc., New Jersey, 2006.         [ Links ]

[16] R. Vaidyanathan, P. Perumal, Structural Analysis, Laxmi Publications (P) LTD, New Delhi, 2005.         [ Links ]

[17] A. Williams, Structural Analysis, Butterworth Heinemann, New York, 2008.         [ Links ]

[18] A. Luévanos Rojas, Method of Structural Analysis for Statically Indeterminate Beams, International Journal of Innovative Computing, Information and Control 8 (2012) 5473-5486.         [ Links ]

[19] A. Luévanos Rojas, Method of Structural Analysis for Statically Indeterminate Rigid Frames, International Journal of Innovative Computing, Information and Control 9 (2013) 1951-1970.         [ Links ]

[20] A. Luévanos Rojas, Method of Structural Analysis, Taking into Account Deformations by Flexure, Shear and Axial, International Journal of Innovative Computing, Information and Control 9 (2013) 3817-3838.         [ Links ]

[21] O.M. González Cuevas, Análisis Estructural, Limusa, México, 2007.         [ Links ]

[22] A. Ghali, A.M. Neville, T.G. Brown, Structural Analysis: A Unified Classical and Matrix Approach, Taylor & Francis, New York, 2003.         [ Links ]

[23]J.C. McCormac, Structural Analysis: using classical and matrix methods, John Wiley & Sons, New York, 2007.         [ Links ]

[24]J.M. Gere, B.J. Goodno, Mechanics of Materials, Cengage Learning, New York, 2009.         [ Links ]

[25]A. Luévanos Rojas, N. Kalashnykova, A. Diosdado Salazar R. Luévanos Rojas, F. Cortés Martínez, Method of Successive Approximations for Statically Indeterminate Rigid Frames Including a New Variable, International Journal of Innovative Computing, Information and Control 9 (2013) 3133-3158.         [ Links ]