Artículos

 

Balanceo de rotores rígidos sin emplear rodados de prueba

 

Enrique S. Gutiérrez Wing¹, Jorge E. Aguirre Romano², Jorge Colín Ocampo¹, Claudia Cortés García¹

 

¹ Departamento de Ingeniería Mecánica, Centro Nacional de Investigación y Desarrollo Tecnológico

² Gerencia de Turbomaquinaria, Instituto de Investigaciones Eléctricas

 

Fecha de recepción: 23-11-2010
Fecha de aceptación: 15-01-2011

 

Resumen

Se presenta un método para la corrección del desbalance de rotores rígidos montados en soportes flexibles. El método se basa en la suposición de que las frecuencias naturales, los factores de amortiguamiento y las formas modales del sistema rotor-soportes pueden obtenerse de la respuesta del rotor a las fuerzas de desbalance que se pretende corregir, medida durante un arranque o un paro. La novedad del método estriba en que, a diferencia de los métodos tradicionales, no se requiere usar modelos numéricos del sistema ni medir su respuesta con fuerzas de desbalance conocidas para determinar la magnitud y posición de las masas que corrijan el desbalance.

El método que se presenta aquí se basa en la relación que existe entre los parámetros modales y espaciales del sistema rotor-soportes. En este trabajo se deducen las ecuaciones que expresan estas relaciones y se describe cómo se utilizan para calcular las masas de corrección del desbalance. La aplicación del método se ilustra mediante un ejemplo numérico.

Este trabajo hace posible balancear rotores rígidos sin la necesidad de ejecutar rodados de prueba, y es considerablemente más simple que otros métodos con el mismo propósito, ya que no se requiere un conocimiento detallado de la geometría o la construcción del rotor.

Palabras clave: Balanceo, Rotores rígidos, Parámetros modales, Modelos numéricos.

 

Abstract

A method for the correction of unbalance in rigid rotors mounted on flexible supports is presented. The method is based on the assumption that the natural frequencies, damping ratios and non-normalized mode shapes can be obtained from the response of the rotor-supports system to the unbalance forces that are to be cancelled-out, using data from a single run-up or run-down. The novelty of the method lies in that, in contrast to traditional methods, neither numerical models nor measurements of the response to known trial unbalances are required in order to determine the magnitude and location of the unbalance correction masses.

The method is based on the relationship that exists between the modal and the spatial parameters of the rotor-supports system. The equations that express such relationships are derived here and their use for the computation of unbalance correction masses is described. The application of the method is illustrated with a numerical example.

This work demonstrates the feasibility of balancing rigid rotors without trial balancing runs, and is considerably simpler than existing balancing methods, since a detailed knowledge of the geometry and construction of the rotor is not required.

Keywords: Balancing, Rigid rotors, Modal parameters, Numerical models.

 

Introducción

El desbalance es una de las causas más comunes de vibración en rotores, se origina en la distribución no uniforme de masa alrededor del centro de rotación del rotor y se corrige mediante el proceso de balanceo.

El balanceo consiste en la adición o eliminación de masas de ubicaciones específicas del rotor. La magnitud de estas masas y su ubicación se seleccionan de manera que las fuerzas centrífugas que actúan sobre ellas al girar el rotor se opongan a las fuerzas producidas por el desbalance original, y de esta manera se contrarresten sus efectos.

Para determinar estas masas y sus ubicaciones los métodos tradicionales de balanceo se basan en esquemas como la determinación de coeficientes de influencia [1], la eliminación selectiva de componentes modales de vibración [2, 3] y combinaciones de ambos [4]. Estos métodos requieren mediciones de la respuesta del rotor a su desbalance original, la cual se mide en un "rodado inicial", y de la respuesta medida en uno o más "rodados de prueba". Un "rodado" es un proceso en el cual el rotor se acelera o se desacelera a través de un intervalo de velocidades preestablecido, de manera que pueda medirse su respuesta vibratoria como función de la frecuencia de excitación. Para el caso de excitación por desbalance esta frecuencia coincide con la frecuencia de giro del rotor.

El "rodado inicial" se usa para medir la respuesta del rotor al desbalance que se pretende eliminar. Este rodado es necesario tanto en los métodos convencionales de balanceo como en el que se propone aquí. Por otro lado, los "rodados de prueba" se usan para determinar los efectos de masas excéntricas conocidas sobre la respuesta del rotor, con el propósito de encontrar un arreglo de éstas que reduzca la amplitud de la respuesta vibratoria a un valor que esté por debajo de límites permisibles [5]. Los rodados de prueba son necesarios en los métodos convencionales de balanceo, pero no en el que se propone aquí.

Las técnicas existentes de balanceo sin rodados de prueba requieren modelos numéricos detallados con los cuales sea posible determinar los coeficientes de influencia del rotor sin la necesidad de medir los efectos del desbalance sobre la respuesta. Estas técnicas se basan en modelos de elementos finitos [6, 7, 8] o de matrices de transición [9].

A pesar de que los trabajos reportados hasta ahora hacen teóricamente posible balancear un rotor sin la necesidad de realizar rodados de prueba, construir un modelo matemático representativo del comportamiento dinámico del rotor requiere un tiempo considerable y en todo caso debe calibrarse mediante datos experimentales.

En este documento se presenta un nuevo método de balanceo con el cual no es necesario conocer los coeficientes de influencia, contar con modelos numéricos del rotor, realizar rodados de prueba ni contar con registros de balanceos previos para determinar las masas de corrección. Únicamente se requieren datos de un rodado inicial, a partir de los cuales puedan determinarse las frecuencias naturales del sistema rotor-soportes, los factores de amortiguamiento de sus modos y las formas modales correspondientes a cada uno. A estos parámetros se les conoce como parámetros modales. Adicionalmente, se requiere conocer la masa del rotor y la de los componentes de los soportes que se muevan con él durante el balanceo. Como se desconocen las fuerzas de desbalance del rotor, las formas modales que se determinan del rodado inicial están escaladas arbitrariamente, de manera que no es posible determinar directamente las matrices de masa, amortiguamiento y rigidez del sistema a partir de la respuesta del rotor en ese rodado.

 

BALANCEO DE ROTORES RÍGIDOS

A pesar de que los rotores normalmente experimentan flexión durante su funcionamiento, comúnmente se balancean en bancos con soportes suaves, en los cuales el rotor puede girar mientras permanece prácticamente rígido. En estas condiciones, la vibración del rotor se debe a la deformación de los soportes de la bancada, causada por las fuerzas de desbalance que se transmiten hacia ellos a través del cuerpo del rotor.

Las técnicas de balanceo de rotores rígidos tienen algunas ventajas sobre las de rotores flexibles: i) la respuesta sólo contiene contribuciones de dos modos de vibración, ii) la respuesta en cualquier punto del rotor puede determinarse a partir de aquella medida en dos puntos cualesquiera, iii) las resonancias ocurren a bajas velocidades, lo cual facilita la obtención de datos de vibración resonante, a diferencia del proceso para rotores flexibles, cuyas resonancias ocurren a altas velocidades. El balanceo de rotores rígidos generalmente se realiza como un paso previo al balanceo fino de un rotor en sus chumaceras con el fin de reducir el desbalance grueso del rotor antes de ponerlo en operación. Como la respuesta de un rotor rígido sólo presenta componentes de dos modos de vibración, su balanceo únicamente requiere dos planos para la colocación de masas de corrección.

 

DINÁMICA DE UN ROTOR RÍGIDO

La Figura 1 muestra un diagrama de un montaje típico para balanceo en bancadas suaves. El rotor está montado en dos soportes flexibles que le permiten desplazarse sólo en dirección vertical. Cada soporte puede modelarse como un sistema de un grado de libertad que contribuye a la masa, la rigidez y el amortiguamiento del sistema rotor-soportes. El sistema tiene dos grados de libertad.

 

Aunque las fuerzas de desbalance están distribuidas a lo largo del rotor, la consideración de que éste permanece rígido hace posible representarlas como una fuerza resultante que actúa en su centro de masa así como un par resultante. Alternativamente pueden representarse mediante dos fuerzas que actúan en planos de balanceo distintos [5].

La ecuación de movimiento del rotor mostrado en la Figura 1 es:

donde M, C y K son matrices reales, simétricas, de dimensiones 2x2 que representan las propiedades inerciales, disipativas y elásticas del sistema rotor-chumaceras.

{x(t)} = {x₁(t) x₂(t)}^T es el vector de respuesta al desbalance en el dominio del tiempo y {f(t)} = {f₁(t) f₂(t)}^T es el vector de componentes verticales de las fuerzas de desbalance.

 

Matriz de masa

Con respecto al sistema coordenado formado por x₁, x₂ y por las fuerzas f₁ y f₂ en la Figura 1, la matriz de masa del rotor es:

donde C.G. denota el centro de masa del rotor, l_CG indica la ubicación de este punto e I_CG es el momento de inercia transversal del rotor con respecto al mismo punto. El procedimiento que conduce a la matriz de masa se presenta en el Apéndice A. La suma de los elementos de la matriz de masa es igual a la masa total del sistema, m_T , esto es:

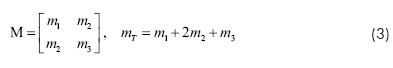
En una sección posterior se mostrará que esta ecuación proporciona un parámetro de escala crucial para la determinación de masas de balanceo para un rotor rígido.

 

Matrices de amortiguamiento y de rigidez

Las características de amortiguamiento y rigidez del sistema que nos ocupa están determinadas por las propiedades de los soportes. Cuando la vibración del rotor se mide en los soportes estas matrices son diagonales, pero en general las matrices son sólo simétricas. La excepción es el caso en que la respuesta del sistema y las fuerzas de excitación se expresan en distintos sistemas coordenados, lo cual puede resultar en matrices asimétricas de amortiguamiento y de rigidez.

En la discusión que sigue, los grados de libertad serán los desplazamientos del rotor en sus soportes y las fuerzas de desbalance se calcularán para estos puntos. A través de transformaciones lineales se calcularán pares de fuerzas que sean equivalentes a las ya calculadas, pero que actúen en los planos de balanceo.

 

Valores y vectores característicos del sistema rotor-chumaceras

Durante un rodado el rotor se acelera o se desacelera lentamente dentro de un intervalo de velocidades que se establece para que el sistema cruce sus dos resonancias, mientras alcanza un estado estable de vibración a cada velocidad dentro de dicho intervalo. Como la distribución de masa que provoca el desbalance del rotor gira con él, las fuerzas centrífugas que actúan sobre el rotor desbalanceado son armónicas con respecto a una dirección espacial fija, por ejemplo la dirección vertical en la Figura 1, y su frecuencia coincide con la frecuencia de giro del rotor. En un sistema lineal esto produce una respuesta también armónica y de la misma frecuencia. La fuerza y la respuesta se representan en forma vectorial en el dominio de la frecuencia a través de:

Sustituyendo estas expresiones en la Ecuación (1), se obtiene la ecuación de movimiento del sistema rotor-soportes en el dominio de la frecuencia [10]:

En el resto de este documento los vectores X(w) y F(w)se expresarán sólo como X y F, respectivamente. La representación de la Ecuación (6) en el espacio de estados es [11]:

donde 0 representa a una matriz de ceros de dimensiones 2x2 y 0_2x1 es un vector de ceros de dimensiones 2x1. Los parámetros modales del sistema se obtienen de la solución al siguiente problema de valores y vectores característicos:

El sistema posee cuatro juegos de valores y vectores característicos, los cuales forman dos pares complejos conjugados y esto se debe a que las matrices del sistema son reales. Los parámetros modales se pueden ensamblar en una matriz de manera que las propiedades espaciales y modales puedan relacionarse mediante una sola ecuación matricial, la cual reúne las cuatro ecuaciones que resultan de la Ecuación (8):

Para el sistema rotor-soportes de dos grados de libertad, los bloques ψ y Λ pueden definirse como:

 

Vectores característicos normalizados

Existen multiplicadores para cada uno de los vectores característicos no-normalizados del sistema, que al ensamblarse en dos matrices, D₁ y D₂ , conducen a una versión normalizada de los vectores a través de [11]:

Por otra parte, existe un juego de vectores característicos normalizados que satisface las transformaciones bilineales que resultan de las siguientes ecuaciones matriciales:

 

RELACIONES ENTRE LOS PARÁMETROS MODALES Y ESPACIALES

Usando las Ecuaciones (12) y (13) es posible expresar las propiedades espaciales del sistema en función de los parámetros modales. Si estas ecuaciones se reescriben como:

y se utiliza la relación Φ ψD₁ , que se deduce de la Ecuación (11), para expresar estas dos últimas ecuaciones en función de los vectores característicos no-normalizados, se llega a las siguientes relaciones entre los parámetros espaciales y modales del sistema:

El interés por utilizar vectores característicos no-normalizados se debe a que éste es el único tipo de vector que puede obtenerse a partir de la respuesta del rotor en un rodado inicial, ya que no se conocen las fuerzas que producen la respuesta.

Las relaciones dadas en las Ecuaciones (17)-(19) pueden escribirse en la siguiente forma simplificada, que se deduce en el Apéndice B:

Las matrices U, V, W, G, M, C y K de las Ecuaciones (23)-(26) tienen dimensiones 2x2. Las matrices U, V y W pueden determinarse del análisis modal de la respuesta al desbalance del sistema rotor-soportes durante el rodado inicial. En contraste, la matriz G no puede determinarse de esas mediciones, dado que es una función de los elementos desconocidos de la matriz D₁.

Ahora se describirá la manera en que pueden utilizarse estas ecuaciones para determinar los elementos g_ij,

Si los elementos de cada una de las matrices de la Ecuación (20) se escriben explícitamente, ésta puede reescribirse de la siguiente manera:

y de aquí puede deducirse la siguiente expresión:

o, alternativamente:

donde es una representación vectorizada de la matriz G.

Similarmente, usando las Ecuaciones (20) y (21) pueden obtenerse las siguientes ecuaciones:

Las Ecuaciones (29)-(31) forman un sistema de ecuaciones homogéneo cuyas incógnitas son los elementos de la matriz G. Se requiere una ecuación adicional para calcular los elementos de G como solución única al sistema. Esta es la Ecuación (4), que expresa la masa total del sistema rotor-soportes como la suma de los elementos de la matriz de masa. Usando esta ecuación junto con la Ecuación (27) se obtiene la siguiente expresión:

o, alternativamente:

Esta ecuación y las Ecuaciones (29)-(31) pueden usarse para determinar los elementos de la matriz G:

Como se mostrará en la siguiente Sección, la matriz G es la base para el cómputo de las masas de balanceo para el sistema.

 

CÁLCULO DE MASAS DE BALANCEO

Utilizando las relaciones entre los parámetros espaciales y modales dadas en la Ecuaciones (12) y (13) se obtiene la siguiente relación entre la respuesta del sistema y las fuerzas de desbalance:

Con base en las relaciones entre los vectores característicos normalizados y los no-normalizados dadas en la Ecuación (11) y en la definición de la matriz G dada en la Ecuación (23), la relación entre la respuesta y las fuerzas de desbalance puede expresarse como:

o alternativamente como:

En esta ecuación las matrices de valores y vectores característicos no-normalizados se obtienen del rodado inicial del rotor, mientras que la matriz G se calcula siguiendo el procedimiento descrito en la sección anterior. Entonces, si el vector de respuesta al desbalance, X , se conoce para cada frecuencia de giro, ω , el vector de fuerzas de desbalance, F, puede determinarse directamente como una función de dicha frecuencia.

Es necesario tener en cuenta que la Ecuación (37) está basada en la suposición de que los desplazamientos del sistema y las fuerzas que actúan sobre él están definidos en los mismos sistemas coordenados. Si se requiere conocer un conjunto de fuerzas equivalentes, {F}_PLANOS, que actuando en los planos de balanceo tenga el mismo efecto que las fuerzas calculadas a través de la Ecuación (37), entonces debe usarse una matriz de transformación, A, tal que:

En esta ecuación la matriz A expresa la relación entre las representaciones de las fuerzas de desbalance en dos sistemas coordenados distintos: uno formado por vectores unitarios en los puntos de medición de vibración, y otro formado por vectores unitarios en los planos de balanceo. Si la vibración se mide en los planos de balanceo entonces A es la matriz identidad. Si se utilizan las siguientes definiciones para la respuesta y las fuerzas de desbalance:

entonces A es la matriz que relaciona los vectores de fuerza {F₁1, F₂} con {F_P1, F_P2} bajo la condición de que ambos vectores tengan la misma fuerza y momento resultantes. Por ejemplo, para el sistema mostrado en la Figura 2, la matriz A es:

 

 

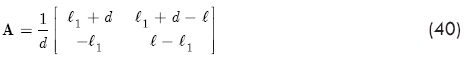
Finalmente, para calcular las masas de balanceo debe considerarse que las fuerzas de desbalance son proporcionales al cuadrado de la velocidad de rotación, así como a las distancias radiales, r_P1 y r_P2 respectivamente, entre el eje del rotor y los pozos para cada uno de los planos de balanceo. Estos parámetros están relacionados mediante:

Las masas de balanceo entonces pueden calcularse con la siguiente ecuación:

donde el signo negativo se añade para expresar que las fuerzas de balanceo son directamente opuestas a las fuerzas que producen la vibración original.

 

PROCEDIMIENTO DE PRUEBA Y DE ANÁLISIS

La aplicación del método de identificación y corrección de desbalance que se presentó en las secciones anteriores se realiza de la siguiente manera:

Paso 1. Medición de la respuesta al desbalance que se desea eliminar durante un arranque o paro del rotor.

Paso 2. Análisis modal de la respuesta. Realizar un análisis modal de la respuesta para determinar las frecuencias naturales, los factores de amortiguamiento y las formas modales no-normalizadas del sistema rotor-soportes.

Paso 3. Construcción de las matrices de parámetros modales. Con los parámetros modales que se identificaron, formar las matrices de valores y vectores característicos, Λ y ψ, respectivamente, de acuerdo con la Ecuación (10).

Paso 4. Cálculo de las matrices U, V y W usando las Ecuaciones (24)-(26). Es importante notar que para el cálculo de estas matrices no requieren los vectores característicos normalizados, sino los no-normalizados que se obtienen del rodado inicial.

Paso 5. Cálculo de los elementos de la matriz G empleando la Ecuación (34).

Paso 6. Cálculo de la matriz de transformación de fuerzas a los planos de balanceo. Si las masas de corrección se colocarán en estaciones del rotor distintas a aquéllas en las cuales se midió la respuesta en el inciso 1, determinar la matriz A a partir de las distancias entre los soportes del rotor y entre éstos y los planos de balanceo, de acuerdo con la Ecuación (40).

Paso 7. Cálculo de las masas de balanceo. Determinar los radios de colocación, r_P1 y r_P2 , de las masas de corrección en cada uno de los planos de balanceo y calcular las masas de corrección de acuerdo con la Ecuación (42).

Como último paso del balanceo se deberán instalar en los planos correspondientes las masas de balanceo que se calcularon.

 

EJEMPLO NUMÉRICO

En esta sección se presenta un ejemplo ilustrativo del uso del algoritmo que se describió en la sección anterior para el cálculo de masas de balanceo. El ejemplo se basa en el rotor que se muestra en la Figura 3. El desbalance que se utiliza es debido a dos masas excéntricas colocadas en el borde exterior de los discos. El método no está limitado a casos con este tipo de desbalance. En general el desbalance puede estar distribuido a lo largo del rotor, pero independientemente de la distribución que tenga, en cualquier caso es posible determinar un desbalance equivalente que produzca el mismo efecto en el rotor que el desbalance distribuido. Esto se discute más ampliamente en el apartado Desbalances equivalentes de la sección Discusión.

Las magnitudes y ángulos de colocación de estas masas se presentan en la Tabla 1. La masa, el amortiguamiento y la rigidez de los soportes se presentan en la Tabla 2. El rotor se considera construido de acero, con una densidad de 7850 kg/m³. La masa del rotor es de 28.94 kg y la masa total del rotor con los soportes es de m_T= 29.94 kg. Los soportes restringen el movimiento del rotor a un plano vertical.

 

 

Paso 1. Medición de la respuesta al desbalance

En este ejemplo numérico se calculó la respuesta al desbalance del rotor, obteniéndose los diagramas de respuesta que se presentan en la Figura 4.

 

Paso 2. Análisis modal de la respuesta

Como puede verse en la Figura 4b, el diagrama polar presenta dos regiones circulares, cada una de los cuales está asociada con un modo de vibración. La resolución de frecuencia que se empleó para elaborar la gráfica es de 6.726 mHz. Los parámetros modales del sistema se determinaron empleando un algoritmo de ajuste de cocientes de polinomios [10] y se presentan en la Tabla 3.

 

Paso 3. Construcción de las matrices de parámetros modales

Empleando los datos de la Tabla 3, las matrices de vectores y valores característicos son, respectivamente:

 

Paso 4. Cálculo de las matrices U, V y W.

Se utilizan las Ecuaciones (24)-(26) con las matrices de parámetros modales que se determinaron en el paso anterior, y con ésto se obtienen los siguientes resultados:

 

Paso 5. Cálculo de los elementos de la matriz G.

Con estas tres matrices y el valor de la masa total del rotor es posible determinar la matriz de coeficientes del lado izquierdo de la Ecuación (34) para posteriormente calcular los elementos de la matriz:

La solución de este sistema es:

La matriz G es entonces

 

Paso 6. Cálculo de la matriz de transformación de fuerzas a los planos de balanceo.

Dado que la ubicación de los planos de balanceo difiere de los puntos en los que se mide la respuesta, es necesario determinar una matriz de transformación para convertir las fuerzas de desbalance que se calculan en fuerzas equivalentes en los planos de balanceo. La matriz de transformación se calcula con la Ecuación (40), que para este ejemplo es:

 

Paso 7. Cálculo de las masas de balanceo.

Si se sustituyen los radios de colocación de las masas de balanceo, r_{p1 ;} and r_p2 respectivamente, en la Ecuación (42), las masas de balanceo que se requieren en cada plano pueden determinarse como funciones de la frecuencia ω. Estas funciones se muestran en la Figura 5. La Ecuación (42) da como resultado valores constantes para las masas de balanceo. Más aún, sus magnitudes son iguales a las de las masas de desbalance que se presentaron en la Tabla 1, pero están colocadas a 180° de aquéllas en cada uno de los planos. En la Tabla 4 se presentan los valores de las masas de desbalance y de las masas de corrección que se calcularon con la Ecuación (42).

 

 

DISCUSIÓN

Análisis comparativo del método propuesto.

A causa de la gran variedad de factores que intervienen en la exactitud del proceso de balanceo, como la exactitud de las mediciones de respuesta, la variabilidad de la respuesta para las mismas condiciones de operación, la exactitud en la construcción de modelos numéricos o experimentales y los métodos de procesamiento de datos, entre otras, una comparación cuantitativa del método propuesto con otros existentes sería demasiado extensa para los límites de este trabajo. Sin embargo es posible analizar algunas ventajas y desventajas del método que se propone aquí .

En la Tabla 5 se comparan algunas características relevantes de varios métodos de balanceo: 1) el método que se propone en este trabajo, 2 y 3) los métodos más comúnmente utilizados en la práctica, y 4, 5 y 6) algunos métodos reportados en la literatura encaminados al balanceo sin rodados de prueba.

 

El método que se presenta aquí, al igual que los métodos 4, 5 y 6 de la Tabla 5, se basa en mediciones de respuesta de un único rodado (llamado rodado inicial). Por lo tanto no es posible evaluar su susceptibilidad a la no-repetitividad de las mediciones. Sin embargo, es posible destacar algunos puntos con respecto a su robustez y compararla de este modo con otros métodos.

El método que se presenta aquí se basa en un análisis modal de la respuesta al desbalance, del cual se obtienen los parámetros modales que correlacionan la respuesta observada a todas las velocidades del rotor dentro del intervalo de prueba. Esta característica global del análisis reduce el impacto que puedan tener los errores de medición a alguna velocidad en particular, característica que comparte con los métodos 3, 5 y 6 de la Tabla 5, y es una de las ventajas que presentan estos métodos con respecto al método de coeficientes de influencia, indicado con el número 2 en la misma tabla. En este último no se hace correlación alguna entre la respuesta medida a diferentes velocidades, lo cual equivale a ignorar el hecho de que las mediciones provienen de un mismo sistema. La consecuencia de esto es que el método de coeficientes de influencia conduce a errores significativos cuando el cálculo de las masas de balanceo se basa en la respuesta medida a alguna velocidad que coincida con la frecuencia de fuentes de excitación distintas al desbalance del rotor, como ruido, resonancias de sistemas adjuntos, etc.

Los métodos 4, 5 y 6 de la Tabla 5 se basan en la suposición de que se cuenta con modelos "correctos" del rotor antes de iniciar el balanceo. Sin embargo, es necesario validar estos modelos experimentalmente para garantizar su aplicabilidad. Por esta razón el hecho de basarse en esta suposición es una de las principales debilidades de estos métodos. Por el contrario, el método que se presenta aquí se basa en un modelo cuyos parámetros se obtienen exclusivamente de mediciones. Esta característica la comparte con los métodos de balanceo modal y de coeficientes de influencia. La ventaja de este enfoque experimental es que no supone valores particulares para ninguno de los parámetros dinámicos del sistema, ya sean modales o espaciales; todos los parámetros se determinan con base en la respuesta real del sistema al desbalance. Los métodos 2-6 requieren como información de inicio ya sea un modelo numérico del rotor o la ejecución de rodados de prueba. La novedad del método que se presenta en este trabajo es que no requiere datos de cualquiera de los dos tipos. Esto se logra utilizando una medición de la masa del rotor en lugar de modelos numéricos para el cálculo de las masas de balanceo.

 

Modos reales

Cuando los vectores característicos o formas modales del sistema rotor-soportes son vectores reales (todos sus elementos están en fase o en contrafase) no es posible determinar los elementos de la matriz G de la Ecuación (34) debido a que la matriz de coeficientes es singular. Esto se debe a que este tipo de sistema corresponde a un modelo con amortiguamiento proporcional [10] y esto hace que las Ecuaciones (20)-(22) sean linealmente dependientes. Para resolver este problema es posible agregar ecuaciones al sistema. Por ejemplo, la siguiente ecuación expresa la condición de que la matriz de rigideces es diagonal:

Esta ecuación puede emplearse cuando la respuesta se mida en los soportes, debido a que los desplazamientos de estos coinciden con las rigideces principales del sistema. Similarmente, y en las mismas circunstancias, puede emplearse la siguiente ecuación, que establece que la matriz de amortiguamientos es diagonal:

 

Desbalances equivalentes

Cualquier combinación de fuerzas que actúe sobre un cuerpo rígido puede reemplazarse por una fuerza y un par resultantes o por dos fuerzas no colineales que actúen en dos puntos distintos del cuerpo.

El desbalance en un rotor generalmente está distribuido a lo largo de éste. Si el rotor permanece rígido entonces es posible encontrar un par de fuerzas que actuando en dos estaciones a lo largo de su eje longitudinal, por ejemplo en las ubicaciones de los planos de balanceo, tengan la misma fuerza y momento resultantes que el desbalance original y por ende el mismo efecto sobre el rotor. Este "desbalance equivalente" es el que se pretende eliminar con el método presentado aquí. El objetivo es determinar un par de masas de corrección localizadas en los planos de balanceo y que sean tales que su efecto sobre el rotor se oponga al de este "desbalance equivalente" en los planos. De esta manera se logra cancelar el desbalance original.

Es importante resaltar que las masas de corrección no corrigen el desbalance del rotor en cada una de sus secciones transversales por separado, sólo corrigen el efecto conjunto del desbalance distribuido.

El punto de partida del ejemplo anterior fue suponer un desbalance localizado en los planos de balanceo. Sin embargo esto no implica que el método sea sólo aplicable a esos casos, sino a todos aquéllos en los cuales pueda encontrarse un desbalance equivalente a dos fuerzas en los planos de balanceo. Bajo la suposición de que el rotor permanece rígido, que es la premisa básica de este trabajo, esto abarca cualquier distribución de desbalance a lo largo del rotor.

 

Ángulo de colocación de las masas de balanceo.

La medición de la respuesta al desbalance tiene dos componentes para cada frecuencia: la amplitud de la vibración y el ángulo de fase de ésta con respecto al paso de una marca fija en el rotor que se detecta por medio de un sensor estacionario, que típicamente es un tacómetro. Para introducir estos dos componentes de la respuesta en la Ecuación (42), con la amplitud y el ángulo de fase medidos a cada frecuencia se forma un número complejo cuyo módulo es la amplitud y cuyo argumento es el ángulo de fase. De esta manera, el vector de respuesta, X, que aparece en dicha ecuación es un vector de números complejos. Las masas de balanceo que se calculan también son números complejos y su ángulo de colocación es igual al argumento de dichos números.

 

CONCLUSIONES

Se ha presentado un método de cálculo de masas de balanceo para un sistema formado por un rotor rígido en soportes flexibles. El método no requiere rodados de prueba, modelos matemáticos detallados ni registros de balanceos previos del rotor. Los resultados obtenidos demuestran que es teóricamente posible balancear un rotor rígido sin rodados de prueba ni modelos detallados, dado que el conocimiento de algunas características dinámicas simples como la masa total complementan a la información referente a las formas, frecuencias naturales y razones de amortiguamiento modales, para hacer posible el cálculo de las masas de balanceo.

 

REFERENCIAS

[1] Thearle, E.L., "Dynamic balancing of rotating machinery in the field", Transactions of the American Society of Mechanical Engineers, Journal of Applied Mechanics, no. 56, pp. 745-753, 1934.         [ Links ]

[2] Parkinson, A.G., Jackson, K.L., Bishop, R.E.D., "Some experiments on the balancing of small flexible rotors: Part I — Theory", Journal of Mechanical Engineering Science, vol. 5, no. 1, pp. 114-128, 1963a.         [ Links ]

[3] Parkinson, A.G., Jackson, K.L., Bishop, R.E.D., "Some experiments on the balancing of small flexible rotors: Part II — Experiments", Journal of Mechanical Engineering Science, vol. 5, no. 2, pp. 133-145, 1963b.         [ Links ]

[4] Parkinson, A. G., Smalley, A. J., Badgley, R. H., Darlow, M. S., An introduction to a unified approach to flexible rotor balancing, American Society of Mechanical Engineers Gas Turbine Conference and Exhibit and Solar Energy Conference, Mar. 12-15 1979, San Diego, CA.         [ Links ]

[5] Rao, J.S., Rotor Dynamics, 3a edición, New Age International, 1996.         [ Links ]

[6] LeGrow, J.V., Multiplane balancing of flexible rotors — A method of calculating correction weights, Paper No. 71-Vibr-52, Toronto, Canada, September 1971.         [ Links ]

[7] Lees, A.W., Friswell, M.I. , The evaluation of rotor imbalance in flexibly mounted machines, Journal of Sound and Vibration, vol. 208, pp. 671-683, 1997.         [ Links ]

[8] Preciado-Delgado, E., Bannister, R.H., "Balancing of an experimental rotor without trial runs", International Journal of Rotating Machinery, vol. 8, 2002.         [ Links ]

[9] Aguirre-Romano, J.E., Cervantes-Contreras, J., Gutiérrez-Wing, E.S., Modal balancing of turbo-generator rotors using simplified spatial models, Proceedings of the ISMA International Conference on Vibration and Noise Engineering, 18-20 September 2006, Leuven, Belgium.         [ Links ]

[10] Ewins, D.J., Modal Testing: Theory, practice and application, 2a. edición, Research Studies Press LTD, Hertfordshire, 2000.         [ Links ]

[11] He, J., Zhu, Z.F., Modal Analysis, Butterworth-Heinemann, Oxford, 2001, pp. 123-139.         [ Links ]