Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería mecánica, tecnología y desarrollo
versión impresa ISSN 1665-7381
Ingenier. mecáni. tecnolog. desarroll vol.3 no.4 México mar. 2010
Artículos
Modelación no lineal de las vibraciones auto-inducidas en procesos de maquinado
Luciano Vela Martínez1, Juan Carlos Jáuregui Correa2, Oscar González Brambila3 Gilberto Herrera Ruiz4, Alejandro Lozano Guzmán4
1CIATEQ Unidad Aguascalientes
2CIATEQ Unidad Bernardo Quintana
3CIATEQ Unidad Aguascalientes
4DEPFI-Universidad Autónoma de Querétaro
Fecha de recepción: 06-11-09
Fecha de aceptación: 27-01-10
Resumen
Las vibraciones auto-inducidas limitan la productividad de los procesos de maquinado de productos metálicos. Se trata de un problema de inestabilidad dinámica que restringe la razón de remoción de material; además, afecta la calidad superficial de las piezas y acelera el deterioro de las herramientas de corte y los elementos mecánicos de los husillos. El fenómeno presenta un comportamiento altamente no lineal de tipo caótico, con bifurcaciones subcríticas Hopf y de período duplicado. En esta investigación se presenta un estudio de las vibraciones auto-inducidas en procesos de maquinado usando técnicas de dinámica no lineal, con el objetivo de predecir con mayor precisión las condiciones de estabilidad en términos de las características dinámicas y de operación del sistema. El estudio se basó en un modelo débilmente no lineal con términos cuadráticos y cúbicos para representar comportamientos no lineales de tipo estructural y regenerativos. Se construyó una solución aproximada mediante el método de escalas múltiples y se establecieron condiciones de inestabilidad debido a bifurcaciones subcríticas Hopf. Una contribución importante fue la identificación del efecto de la histéresis en los diagramas de estabilidad convencionales, lo cual puede ser útil para restablecer la estabilidad. El modelo analítico se validó experimentalmente, el comportamiento de histéresis se identificó exitosamente a partir de la medición de la respuesta dinámica del sistema.
Palabras clave: Vibraciones auto-inducidas, estabilidad dinámica, histéresis.
Abstract
Self-excited vibrations limit the productivity of machining processes in metallic products. These vibrations originate dynamic instability problems that hinder the rate of removal of material, as well as affect the surface quality of the pieces and accelerate the wear of the cutting tools and the mechanical elements of spindles. This phenomenon presents a highly non-linear chaotic behavior characterized by both subcritical Hopf and doubling period bifurcations. This research deals with self-excited vibrations in machining processes using non-linear dynamic techniques with the aim of predicting with more accuracy the stability conditions in terms of dynamic characteristics and operating conditions of the system. This study is based on a weakly non-linear model with square and cubic terms that represent structural and regenerative nonlinearities. An approximate solution was derived using the multiple-scale method; instability conditions were established due to subcritical Hopf bifurcations. A major contribution of this study is the identification of hysteresis in the conventional stability diagrams, which may be useful to reestablish stability. The analytical model was validated experimentally; the nonlinear behavior of hysteresis was successfully identified by measuring the dynamic response of the system.
Key words: Chatter, dynamic stability, hysteresis.

INTRODUCCIÓN
La modelación analítica de las vibraciones auto-inducidas en maquinado es un tema de interés actual, tanto en la academia como en la industria, por sus implicaciones en la productividad de los procesos de maquinado. Taylor (1907) identificó un tipo de vibración auto-inducida como una limitante de la productividad en procesos de corte. Sin embargo, las explicaciones teóricas sobre la generación de este tipo de vibraciones se presentaron posteriormente; tales como amortiguamiento negativo (Arnold, 1946), regeneración del espesor de viruta (Tobias y Fishwick, 1958), dinámica estructural (Tlusty y Polacek, 1963; Merrit, 1965), así como fricción seca y acoplamiento modal (Wu y Liu, 1985 a, b). Actualmente, la teoría de regeneración del espesor de viruta se considera la explicación más completa, donde el término desestabilizador se introduce en la fuerza de corte como una función del paso previo de corte y el paso actual. Los trabajos en esta línea de investigación han sido presentados por Budak y Altintas (1998), y Altintas (2000), entre otros. Uno de los resultados más importantes del análisis predictivo de las vibraciones auto-inducidas es la caracterización de la estabilidad dinámica de un sistema de maquinado a través de las curvas de estabilidad. Por otro lado, el análisis no lineal se inició con Hanna y Tobias (1974), quienes propusieron un modelo dinámico con no linealidades de tipo cuadrático y cúbico, tanto en la rigidez como en la fuerza de corte. Los parámetros no lineales se calcularon a partir de mediciones experimentales de fuerza de corte y respuesta dinámica, y se verificó el comportamiento no lineal. Este modelo se resolvió posteriormente mediante técnicas de análisis no lineal como métodos de perturbación y balance armónico (Pratt, 1997). De este análisis se concluyó que el fenómeno de vibraciones auto-inducidas estaba caracterizado por la presencia de ciclos límite y el fenómeno de salto, atribuidos a los términos de rigidez no lineales. Stépán et al. (2005a, 2005b) representaron la fuerza de corte mediante un modelo dinámico no lineal de tipo exponencial, propuesto por Tlusty (2000). Mediante una expansión binomial de la función exponencial se obtuvieron términos cuadráticos y cúbicos de tipo regenerativo, aunque no se consideró la no linealidad de la rigidez; sin embargo, este modelo permitió encontrar bifurcaciones de doble período (bifurcación flip) en el mapa de estabilidad. Otros estudios (Kalmár-Nagy et al, 2001; Mann et al, 2004; Moon et al, 2001) aplicaron técnicas de bifurcaciones, teoría de manifold central, y secciones de Poincaré para analizar el comportamiento caótico de las vibraciones auto-inducidas. De acuerdo con los resultados obtenidos, también se confirmó la existencia de un comportamiento inestable de doble período.
De la discusión anterior se establece como hipótesis que el problema de vibraciones auto-inducidas se puede representar por medio de un modelo no lineal con términos estructurales y regenerativos de tipo cúbico, caracterizado por la presencia del fenómeno de salto o histéresis en la función de respuesta a la frecuencia, similar a un modelo de Duffing (Nayfeh et al, 1979). En este trabajo se presentan los resultados del análisis no lineal del fenómeno de las vibraciones auto-inducidas mediante un modelo no lineal con términos regenerativos y estructurales de tipo cúbico, resuelto con el método de escalas múltiples (Vela-Martínez, 2008). Se identificó el efecto de la histéresis de la solución teórica sobre el diagrama de estabilidad convencional del proceso, lo cual puede ser útil para restablecer la estabilidad. El modelo analítico se validó experimentalmente mediante el estudio de las señales del proceso de corte con técnicas espectrales y de ondeletas (wavelets). El comportamiento no lineal del fenómeno quedó establecido mediante la medición de la respuesta dinámica del proceso. Este trabajo representa la culminación de una investigación doctoral (Vela-Martínez, 2008), como parte de las investigaciones en la medición y análisis de vibraciones, así como la optimización de procesos de manufactura (Jáuregui Correa et al, 2005; Rubio Cerda et al, 2006), que se llevan a cabo en el laboratorio de diseño del producto de CIATEQ Unidad Aguascalientes.
DESARROLLO
Uno de los modelos más representativos del comportamiento dinámico no lineal de las vibraciones auto-inducidas en procesos de maquinado, es el propuesto por Hanna y Tobias (1974), el cual contiene términos polinomiales de tipo cuadrático y cúbico para representar no linealidades:

Fenómeno de salto.
La ecuación (1) se puede considerar como un modelo débilmente no lineal (Nayfeh et al, 1979), por lo tanto se espera que presente el fenómeno de salto asociado a la presencia de bifurcaciones subcríticas en el espacio de fase del sistema (Nayfeh et al, 1979; Strogatz, 1994). Este comportamiento está presente en el modelo clásico de Duffing:

El fenómeno de salto es un cambio súbito en la función de respuesta a la frecuencia (Nayfeh et al, 1979). Si la frecuencia se incrementa gradualmente, la amplitud de la respuesta aumenta hasta un valor máximo; sin embargo, cerca de la resonancia la amplitud decae repentinamente y continúa descendiendo a medida que la frecuencia sigue en aumento. Si se repite este proceso pero ahora partiendo de un valor alto de frecuencia, la amplitud aumenta gradualmente a medida que la frecuencia disminuye y presenta una nueva caída repentina cerca de la resonancia. Sin embargo, no existe repetibilidad con la amplitud del proceso previo sino que, existe una histéresis en la función de respuesta a la frecuencia.
Análisis de perturbación de modelo débilmente no lineal
El modelo débilmente no lineal (1) puede representar un proceso de torneado de un grado de libertad, como se muestra en la Figura 1.

La fuerza de corte, en el lado derecho de la Ecuación (1), se considera como una función exponencial que obedece a la regla de 3/4 (Tlusty, 2000):
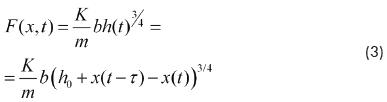
Entonces, la variación de la fuerza de corte se puede aproximar mediante una serie de Taylor de tercer grado con respecto a la variación del espesor de la viruta, como sigue:

Sustituyendo la expansión de la función del espesor dinámico de viruta (4) en la ecuación (1), se obtiene la siguiente expresión:

Empleando el método de escalas múltiples en osciladores débilmente no lineales, como lo proponen Pratt (1997) y Nayfeh y Mook (1979), la función x(t) se expresa como una expansión de tercer orden de la siguiente manera:
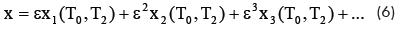
Por consistencia con la expansión de la ecuación (6), la profundidad de corte también se afecta por un esquema de perturbación como sigue:

El parámetro ε también se puede utilizar para expresar perturbaciones pequeñas en el proceso, ya sea variaciones en las propiedades mecánicas del material o variaciones en la profundidad de corte.
La solución aproximada (6) se construye con el método de escalas múltiples, como se describe en Vela-Martínez (2008). El método consiste en sustituir primeras y segundas derivadas de la ecuación (6) en la ecuación (5). Posteriormente se construyen soluciones parciales a partir de condiciones de solubilidad y estabilidad del sistema dinámico. El resultado obtenido es:
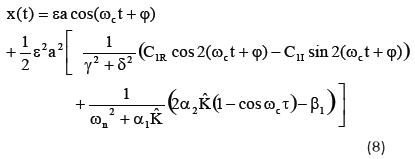
donde los coeficientes de la ecuación anterior se presentan en el Anexo de este artículo.
Análisis de estabilidad y fenómeno de salto
De la primera aproximación a la solución aproximada de (5), se obtiene que la estabilidad dinámica del sistema lineal está gobernada por las siguientes ecuaciones, con las cuales se construye el diagrama de estabilidad mostrado en la Figura 2.
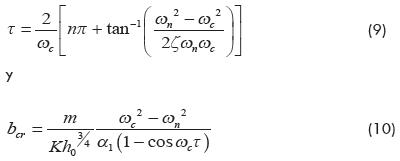

Durante el proceso de construcción de la solución aproximada (6), el sistema dinámico se sintetizó en la siguiente forma normal:

donde los coeficientes c1, c2, c3 y c4 se definen en el Anexo de este artículo.
La estabilidad del sistema dinámico en dos dimensiones, definido por las ecuaciones (1 1) y (12), se puede determinar a partir de la naturaleza de los valores característicos de su Jacobiano (Strogatz, 2004). Si un sistema dinámico general se representa en la siguiente forma normal:

los valores característicos del Jacobiano del sistema están dados por λ= μ ± jω. Aquí, |J controla la estabilidad del punto fijo en el origen, mientras que w proporciona la frecuencia de oscilaciones infinitesimales. Entonces, el sistema es estable siempre que Re(λ) < 0 para ambos valores característicos, los cuales pueden ser reales y negativos o complejos conjugados con parte real negativa. Puesto que el modelo original de la ecuación (1) es autónomo, existen dos posibilidades para la pérdida de estabilidad: bifurcaciones subcríticas (Hopf), cuando el par de valores característicos complejos cruza el eje imaginario del plano complejo hacia la derecha; o bifurcaciones tipo nodo silla, cuando un valor característico real y negativo cruza el eje imaginario en cero (Strogatz, 1994). Previo a la bifurcación, cuando μ < 0, las trayectorias permanecen entre un ciclo límite inestable y un punto fijo estable en el origen, ambos rodeados por un ciclo límite de gran amplitud. A medida que el parámetro de bifurcación μ tiende a cero, el ciclo límite inestable encoge hasta reducir su amplitud de manera que el origen se vuelve inestable y las trayectorias saltan hacia el ciclo límite estable de gran amplitud. Puesto que el origen ahora es inestable, las oscilaciones de gran amplitud no se pueden eliminar con sólo disminuir el parámetro |J a cero, sino que ahora es necesario llevar el parámetro de bifurcación por debajo de cero. Este comportamiento refleja la presencia de histéresis en el sistema, también conocido como fenómeno de salto, típico de problemas de ingeniería que involucran fricción (Nayfeh y Mook, 1 979) y rigidez o excitación variable (González-Brambila, 2006).
De un análisis de valores característicos del modelo dinámico, definido por las ecuaciones (13) y (14), se obtiene uno de los resultados más interesantes de esta investigación. En la Figura 3 se muestra una línea interrumpida sobrepuesta al diagrama de la Figura 2, la cual representa los valores característicos con parte real cercana a cero del lado positivo, a un valor de 5 x 10-15. Esto significa que una vez que la estabilidad se pierde y la parte real de los valores característicos se vuelve positiva, la profundidad de corte deberá ser reducida hasta un valor inferior a aquél que causó la inestabilidad. Este hecho confirma nuevamente la condición subcrítica y la histéresis de la bifurcación. Como se puede apreciar, el rango de histéresis es más amplio a bajas profundidades de corte, lo cual es confirmado experimentalmente más adelante. Este resultado puede ser utilizado para establecer una técnica de restauración de la estabilidad en procesos de maquinado.

Por otro lado, si se analiza la amplitud de la respuesta dada por la ecuación (8), se encuentra que las dos series de lóbulos mostrados en la Figura 3 representan zonas con movimientos de gran amplitud, lo cual coincide con el análisis de estabilidad a partir de los valores característicos, como se muestra en la Figura 4.

VALIDACIÓN EXPERIMENTAL
Para la validación experimental del modelo descrito en la sección anterior, se realizaron pruebas de corte en una máquina fresadora CNC 1 250C modelo Arrow marca CINCINNATI con motor de 12 kW, y un cortador recto de carburo 1 2.7 mm X 25.4 mm de 4 filos marca MASTERCUT. La pieza de trabajo fue una placa de aluminio 6061 con dimensiones 50.8 mm x 203.2 mm x 304.8 mm.
Primero se realizó una prueba de impacto para determinar los parámetros modales del sistema. En la Figura 5 se puede ver un esquema de la prueba en donde se utilizó un martillo instrumentado modelo 9724 marca KISTLER, con una sensibilidad de 2.276 mV/N, para excitar el sistema. La respuesta se midió con un acelerómetro biaxial ±2g modelo ADXL31 1 marca ANALOG DEVICES, con una sensibilidad de 174 mV/g, colocado en la punta del cortador; las señales de ambos dispositivos se acondicionaron y se enviaron a una tarjeta de adquisición de datos (DAQ) para ser procesadas en una computadora (PC) mediante un analizador programado en Matlab. Los parámetros modales encontrados fueron: ωn = 335 Hz, k = 1.3 x108 N/m, y ζ = 0.73%. Además, se consideraron los siguientes coeficientes de corte, Kt = 600 x 106 N/m2 y Kr = 0.3 Kt para aluminio (Altintas, 2000).

Con los parámetros modales y los coeficientes de corte se construyó la curva de estabilidad utilizando un modelo lineal de dos grados de libertad, en donde se consideró que la estructura presentaba las mismas características dinámicas en los dos grados de libertad (Altintas, 2000). En la Figura 6 se muestra la curva de estabilidad en la cual se identificó un punto crítico de mínima estabilidad en 1.55 mm y 2000 rpm para propósitos de análisis en este trabajo.

Se realizaron seis pruebas de corte alrededor del punto crítico y se midieron los niveles de energía de las señales con un micrófono unidireccional DM-20SL. Los experimentos consistieron en realizar un corte a 1, 2 y 5 mm de profundidad, haciendo un barrido ascendente de velocidades del husillo entre 1500 y 2700 rpm con incrementos de 100 rpm para cada corte. Se repitieron los tres experimentos pero con un barrido descendente de la velocidad, entre 2700 y 1500 rpm con decrementos de 100 rpm. Se empleó un avance de 300 mm/min y cada velocidad de husillo se mantuvo durante 25 mm para completar la longitud total de la pieza. El arreglo experimental se ilustra en la Figura 7.
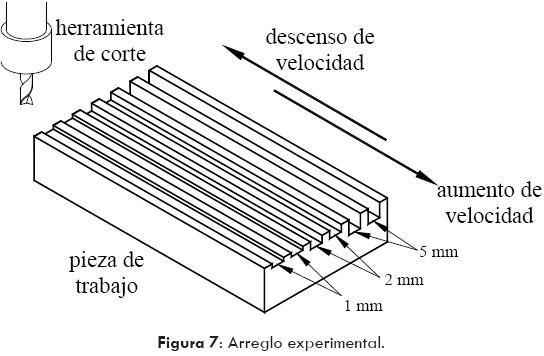
En la Figura 6 también se identifican las zonas de experimentación en la curva de estabilidad, las líneas sólidas corresponden a los cortes de 1 mm, las líneas interrumpidas representan los cortes de 2 mm, mientras que las líneas interrumpidas con punto simbolizan los cortes a 5 mm; la flecha indica el sentido ascendente o descendente de la velocidad del husillo. Por su parte, en la Figura 7 se ilustra el experimento descrito en el párrafo anterior.
En cada prueba se registró el sonido de la señal con el micrófono a una razón de 5000 muestras por segundo y se guardaron los valores de voltaje para cada prueba. Con los datos obtenidos se construyó la curva de respuesta a la frecuencia correspondiente a cada experimento, mediante la amplitud media cuadrática de la señal (rms, por sus siglas en inglés) en bloques de 512 datos. Las curvas de respuesta correspondientes a la misma profundidad de corte se superpusieron para reflejar la histéresis de la respuesta en condiciones de inestabilidad, como se muestra en la Figura 8, para a) 5 mm, b) 2 mm y c) 1 mm de profundidad de corte, respectivamente. Las líneas sólidas (color azul) corresponden al barrido ascendente de velocidad, mientras que las líneas interrumpidas (color rojo) representan el barrido descendente de velocidad.
DISCUSIÓN DE RESULTADOS
De acuerdo con los resultados teóricos de la Figura 6, el corte a una profundidad de 1 mm representa un proceso estable en cualquier condición. El corte a una profundidad de 2 mm inicia en una condición de inestabilidad para entrar a una zona estable y volver a perder la estabilidad entre 1 850 y 2150 rpm; el resto del corte es en régimen estable. Con respecto al corte a 5 mm, éste inicia en una condición de inestabilidad y entra a una zona estable entre 1600 y 1800 rpm; posteriormente entra en un régimen inestable hasta 2300 rpm para volver a perder la estabilidad el resto del recorrido.
Por otro lado, los resultados experimentales de la Figura 8 concuerdan con las predicciones de la curva de estabilidad; se aprecia claramente que la amplitud de las vibraciones aumentó con la profundidad del corte; también se observa un mismo patrón de vibración durante el recorrido ascendente y descendente, aunque no hay una repetibilidad muy marcada en todo el recorrido. El corte a 1 mm de profundidad, Figura 8c, muestra una amplitud de la señal muy baja pero en general se puede apreciar el mismo patrón de vibraciones, principalmente en los extremos del recorrido. En el corte a 2 mm de profundidad, Figura 8b, se aprecia claramente el arranque en condiciones inestables con una amplitud considerablemente alta; la siguiente zona de inestabilidad está definida entre 1900 y 2200 rpm, como se esperaba, pero se aprecia una histéresis muy marcada alrededor de 2000 rpm. La amplitud de la vibración es mayor en el recorrido descendente, lo cual representa una suavización de la rigidez del sistema. Finalmente, en la Figura 8a se muestran los resultados para el corte a 5 mm; se identifican cuatro zonas de histéresis, lo cual coincide con los cuatro puntos de inestabilidad de la Figura 6. El fenómeno de salto con endurecimiento de la rigidez se puede apreciar entre 1950 y 2250 rpm, en condiciones de inestabilidad severa.

Actualmente se está trabajando en la aplicación de técnicas modernas para la detección de inestabilidades dinámicas, tales como la transformada de ondeletas (wavelets) y técnicas de análisis fractal, con el objetivo de desarrollar sistemas de monitoreo y detección en línea. En la Figura 9 se representan los coeficientes de escala y posición, obtenidos de la descomposición jerárquica de la señal correspondiente al experimento con profundidad de corte de 5 mm y velocidad ascendente, entre 1500 y 2700 rpm, mediante la ondeleta madre Paul, debido a que ésta es más conveniente para descomponer patrones con una razón señal/ interferencia alta y variaciones de fase rápidas, esto es, señales con alto contenido de inestabilidad (Lertrattanapanich y Ahuja, 2005). Como se puede ver, la distribución de energía está asociada a la amplitud de las vibraciones, lo cual permitirá establecer criterios de estabilidad en términos de tales coeficientes. También se están evaluando otras técnicas de detección como secciones de Poincaré experimentales (Bayly et al, 2003) y análisis de re-escalamiento (Alvarez-Ramirez et al, 2002).

CONCLUSIONES
En este trabajo se presentó un análisis de perturbación para construir una solución aproximada del modelo débilmente no lineal para la predicción de vibraciones auto-inducidas en procesos de maquinado. A partir de la solución aproximada se establecieron condiciones de inestabilidad debido a bifurcaciones subcríticas Hopf, a partir del análisis de los valores característicos del sistema dinámico en su forma normal. Una contribución importante de este análisis es la representación de la histéresis del sistema en las curvas de estabilidad convencionales, por medio de nuevas curvas intermedias, lo cual puede ser útil para establecer técnicas de restauración de la estabilidad. Se confirmó que el término estructural de tipo cúbico genera el fenómeno de salto en la función de respuesta a la frecuencia, alrededor de la frecuencia natural, la cual es más notoria en condiciones de inestabilidad dinámica severa. Con base en este análisis, se diseñó un experimento para medir el comportamiento no lineal en procesos de maquinado. Los resultados coincidieron con un análisis de estabilidad basado en la prueba de impacto. Los experimentos realizados confirmaron que las vibraciones auto-inducidas presentan el fenómeno de salto alrededor de su frecuencia natural o alguno de sus armónicos.
REFERENCIAS
Altintas Y., 2000, Manufacturing automation, metal cutting mechanics, machine tool vibrations, and CNC design, Cambridge University Press, New York. [ Links ]
Alvarez-Ramirez, J., Cisneros, M., Ibarra-Valdez, C., Soriano, A., 2002, Multifractal Hurst analysis of crude oil prices, Physica A: Statistical Mechanics and its Applications 313 (3 - 4), 651 - 670. [ Links ]
Bayly, P. V., Halley, J. E., Mann, B. P., y Davies, M. A. 2003, Stability of interrupted cutting by temporal finite element analysis. Journal of Manufacturing Science and Engineering Trans. of the ASME 125 (2): 220 - 225. [ Links ]
Budak E., y Altintas Y., 1998, Analytical prediction of chatter stability in milling-Part I: General formulation", Transactions of the ASME Journal of Dynamic Systems, Measurement and Control, Vol. 120, 22 - 30. [ Links ]
González-Brambila O. M., 2006, Simulación de sistemas dinámicos con desprendimiento de contacto que presentan fenómeno de salto, Tesis de doctorado, Facultad de Ingeniería Universidad Autónoma de Querétaro. [ Links ]
Hanna N. H., y Tobias S. A., 1974, A theory of nonlinear regenerative chatter, Transactions of the ASME Journal of Engineering for Industry, Vol. 96, 247 - 255. [ Links ]
Jáuregui Correa, J. C., Urbiola Soto, L., Díaz Díaz, C. y Aboites Dávila, F., 2005, Modelado multidimensional de sistemas viscoelásticos, Ingeniería Mecánica. Tecnología y Desarrollo, Vol. 2 (1), 6 - 12. [ Links ]
Kalmár-Nagy T., Stépán G., y Moon F. C., 2001, Subcritical Hopf bifurcation in the delay equation model for machine tool vibrations, Nonlinear Dynamics Vol. 26, 121 — 142. [ Links ]
Lertrattanapanich S. y Ahuja N., 2005, Properties determining choice of mother wavelet, IEE Proceedings: Vision, image and signal processing, Vol. 152, 659 - 664. [ Links ]
Mann B. P., Bayly P. V., Davies M. A., y Halley J. E., 2004, Limit cycles, bifurcations, and accuracy of the milling process, Journal of Sound and Vibration Vol. 277, 31 - 48. [ Links ]
Merrit H. E., 1965, Theory of Self-Excited Machine Tool Chatter, Trans. ASME Journal of Engineering for Industry, Vol. 87, 447 — 454. [ Links ]
Moon F. C., y Kalmár-Nagy T., 2001, Nonlinear models for complex dynamics in cutting materials, Phil. Trans. Royal Society London Vol. 359, 695 - 711. [ Links ]
Nayfeh A. H., y Mook D. T., 1979, Nonlinear Oscillations, John Wiley & Sons, USA. [ Links ]
Pratt J. R., 1997, Vibration control for chatter suppression, Doctor of Philosophy in Engineering Mechanics Thesis, Virginia Polytechnic Institute and State University. [ Links ]
Rubio Cerda, E., Jáuregui Correa, J. C., y González Brambila, O., 2006, Aplicación de la transformada Wavelet en la detección de defectos por vibrado en piezas cilindricas rectificadas, Ingeniería Mecánica. Tecnología y Desarrollo, Vol. 2 (2), 47 - 52. [ Links ]
Stépán G., Szalai R., Mann B. P., Bayly P. V., Insperger T., Gradisek J., y Govekar E., 2005, Nonlinear dynamics of high-speed milling — Analyses, numerics and experiments, ASME Journal of Vibration and Acoustics, Vol. 127, 197 - 203. [ Links ]
Stépán G., Insperger T., y Szalai R., 2005, Delay, parametric excitation, and the nonlinear dynamics of cutting processes, International Journal of Bifurcation and Chaos, Vol. 15 (9), 2783 - 2798. [ Links ]
Strogatz S. H., 1994, Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering, Fifth Edition, Perseus Books, USA. [ Links ]
Tlusty J., y Polacek M., 1 963, The Stability of Machine Tools against Self Excited Vibrations in Machining, International Research in Production Engineering ASME, 465 - 474. [ Links ]
Tlusty J., 2000, Manufacturing processes and equipment, Prentice Hall, New Jersey. [ Links ]
Tobias S. A., and Fishwick W., 1958, A theory of regenerative chatter, The Engineer-London. [ Links ]
Vela-Martínez L., 2008, Modelación no lineal de las vibraciones auto-inducidas en procesos de maquinado, Tesis de doctorado, Facultad de Ingeniería Universidad Autónoma de Querétaro. [ Links ]














