Artículos

 

Pressure Drop Models Evaluation for Two-Phase Flow in 90 Degree Horizontal Elbows

 

¹Sánchez Silva F., ²Luna Resendiz J. C., ¹Carvajal Mariscal I., ³Tolentino Eslava R.

 

¹Laboratorio de Ingeniería Térmica e Hidráulica Aplicada, IPN-SEPI-ESIME Zacatenco

²Unidad Profesional Interdisciplinaria en Ingeniería y Tecnologías Avanzadas (UPIITA)

³Departamento de Ingeniería en Control y Automatización, IPN-ESIME Zacatenco

 

Fecha de recepción: 18-11-09
Fecha de aceptación: 11-12-09

 

Resumen

En este trabajo se presenta la comparación de datos experimentales y los resultados obtenidos de cuatro modelos globales -homógeneo, Dukler, Martinelli y Chisholm, empleados para evaluar la pérdida de presión en codos horizontales de 90°-. Se realizó una investigación usando tres codos de 90° de acero inoxidables (E1, E2, E3), con diámetros internos de 26.5, 41.2 y 52.5 mm, y radios de curvatura de 194.0, 264.0 y 326.6 mm respectivamente. De acuerdo a los resultados experimentales, el modelo propuesto por Chisholm se ajustó mejor a estos, presentando para cada codo un error promedio de E1 = 1 8.27%, E2 = 28.40% y E3 = 42.10%. Se desarrollaron dos correlaciones basadas en los datos experimentales. La primera es el modelo de Chisholm modificado para obtener mejores resultados en un intervalo más amplio de condiciones; éste se ajustó mediante una relación adimensional que es función de la fracción volumétrica homogénea y del número de Dean. Como resultado, los cálculos empleando el modelo de Chisholm modificado se mejoraron presentando un error promedio de 8.66%. La segunda correlación desarrollada está basada en el flujo másico bifásico total considerado como líquido y corregido por la relación de la fracción volumétrica homogénea. Los resultados mostraron que esta correlación es más sencilla y exacta que el modelo de Chisholm modificado, ésta presentó un error promedio de 7.75%. Por lo tanto, esta correlación se recomienda para evaluar la pérdida de presión de flujos bifásicos en codos horizontales.

Palabras clave: Flujo bifásico, pérdida de presión, codo de 90° horizontal, modelo de Chisholm, número de Dean.

 

Abstract

The comparison of experimental data and results obtained from four global models — homogeneous, Dukler, Martinelli and Chisholm, used to evaluate the two-phase flow pressure drop in circular 90° horizontal elbows - is presented in this paper. An experimental investigation was carried out using three galvanized steel 90° horizontal elbows (E1, E2, E3) with internal diameters of 26.5, 41.2 and 52.5 mm, and curvature radii of 194.0, 264.0 and 326.6 mm, respectively. According to the experimental results, the model proposed by Chisholm best fitted them, presenting for each elbow an average error of E1= 1 8.27%, E2= 28.40% and E3= 42.1 0%. Based on experimental results two correlations were developed. The first one is the classical Chisholm model modified to obtain better results in a wider range of conditions; it was adjusted by a dimensionless relationship which is a function of the homogeneous volumetric fraction and the Dean number. As a result, the predictions using modified Chisholm model were improved presenting an average error of 8.66%. The second developed correlation is based on the entire two-phase mass flow taken as liquid and corrected by the homogeneous volumetric fraction ratio. The results show that this last correlation is easier and accurate than the adjusted Chisholm model, presenting an average error of 7.75%. Therefore, this correlation is recommended for two-phase pressure drop evaluation in horizontal elbows.

Key words: Two-Phase flow, pressure drop, 90° horizontal elbow, Chisholm model, Dean number.

 

 

Introduction

In most of the industrial processes fluids are used as row materials, in power hydraulic systems, as a material transport medium, and many other applications. The complete knowledge of the principles that rule the phenomena involved in fluids transportation leads not only to their better handling but also to more efficient and secure systems. However, in certain industries, such as chemical, geothermal, nuclear and oil, fluids mainly are present as two-phase flow (Hetsroni, 1982).

Heat, mass and momentum transfer enhancement are some of the effects produced by the simultaneous presence of several phases in a mixture. Two-phase flow generally produces a higher-pressure drop in the piping components, which is not desirable in the system. Therefore, a reliable model for the pressure drop prediction in pipelines and fittings for two-phase flows is needed.

In industrial installations, among others, elbows are widely-used fittings. In order to give flexibility to the system, they are used to direct the flow; moreover, they can be used as primary elements to measure the mass flow rate flowing through them (Hernández Ruíz, J., 1 998; Sánchez Silva, et al, 2003; Chan, et al, 2006). Since these fittings are also used to install instruments to monitor the main parameters of industrial processes, and the right location is a crucial factor to have good measurements, so it is important to have a reliable method to evaluate pressure drop in elbows (Chan, et al, 2006).

Below, a review of recent studies regarding pressure drop in elbows is presented. Mandal S. N., and Das S. K. (2001), evaluated pressure drop on different types of horizontal bends for gas-liquid flow and developed correlations to predict the two-phase friction factor. After comparing the predicted values from Chisholm correlation and the measured values of the frictional pressure drop for 90° bends, they found an average relative error of 30.393%. Azzi A. and Friedel L. (2005) carried out an experimental study of air-water flow pressure loss in a vertical bend and proposed a prediction model based on a two-phase flow multiplier. They found a logarithmic ratio scatter, of the experimental and the predicted values, of around 25%. This result is lower than the obtained with some models recommended in the literature, such as Chisholm model and extended homogeneous flow model of which they found a logarithmic ratio of 40% and 33%, respectively. Kim et al (2008) investigated the geometry effect of 45° and 90° elbows on the pressure drop in horizontal bubbly flow. They compared the experimental pressure loss results in elbows with the ones obtained from the Lockhart-Martinelli correlation. They found that the correlation failed to predict the pressure drop, so they developed a new correlation analogous to Lockhart and Martinelli's. Applying the new correlation, with C=65 and the minor loss factors of k=0.58 and 0.35 for the 90° and 45° elbows respectively, they got an average percent differences, between the predictions by the new correlation and the data, of ±2.1% and ±1.3% for the 90° and 45° elbows respectively. The motivation of this paper is to develop simply and accurate correlations for two-phase flow pressure drop evaluation in 90° horizontal elbows. To achieve this objective, three models developed for calculating the pressure drop on straight pipes - homogeneous, Dukler and Lockhart-Martinelli - and a model obtained for estimating the pressure drop on fittings - Chisholm - will be used to evaluate the two-phase pressure drop in circular 90° horizontal elbows. In the case of the former models an equivalent length, which considers the elbows effect, was included.

There has been some efforts to develop more accurate models, Kim Seungjin et al, (2006), and Savalaxs Supa-Amornkul et al, (2005) among others, but due to the two phase flow complexity in elbows, it is necessary to include more parameters to describe the phenomenon, that is why the industry is still using correlations, so the role of experiments and the parametric measurements is particularly important.

 

Experimental Set Up

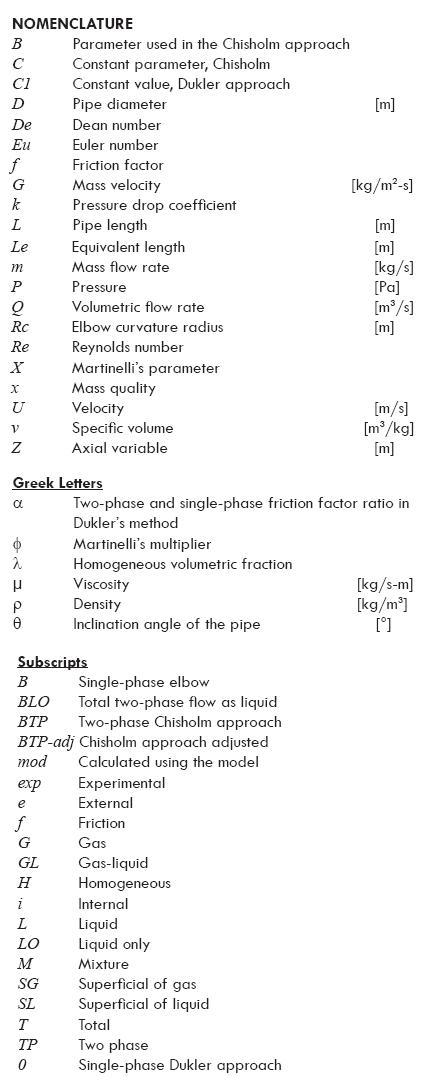
In order to obtain the data used for comparison with the four global models of two-phase flow pressure drop evaluation, a research was carried out in an experimental facility designed to study and visualize low pressure air-water two-phase flows. The experimental facility is integrated by an air supply, water supply, flow measurement section, an experimental section, and phase separation sections (figure 1).

 

The air supply section includes two alternative air compressors of 10 and 5 HP connected in parallel; each one has its own storage tank. At the exit of the tanks a pressure regulation valve allows to keep the sonic flow condition, and then a stable flow condition in the test section is maintained. On the other hand, water supply section consists of a 0.5 m³ main water tank, a 5 HP centrifugal pump and a galvanized steel pipe. This pipe has a recirculation valve in order to reduce the pressure at pump discharge when the experiments require small flows.

Both water and air mass flow rate measurement systems are composed of a couple of 52.8 mm internal diameter pipes connected in parallel. The measurement elements are two orifice plates, installed and calibrated according to the ISO-5167, and the BS 1042 standards for pressure differential devices, 1981.

Once the flow rates are measured, both are conducted to a 30° Y mixer. The resulting mixture continues through a 25.6 m long pipe in order to have a developed flow before the test section, which is interchangeable, in order to test other diameters. After it, the two-phase flow passes through a pipe section of 4.9 m and discharges into a cyclone separator, which has a deflector that makes the water level to descend gradually. Finally, a 1 HP pump returns the water to the suction tank, and the separated air is vented to the atmosphere Hernández Ruíz J. (1998), and Luna Reséndiz J. C. (2002).

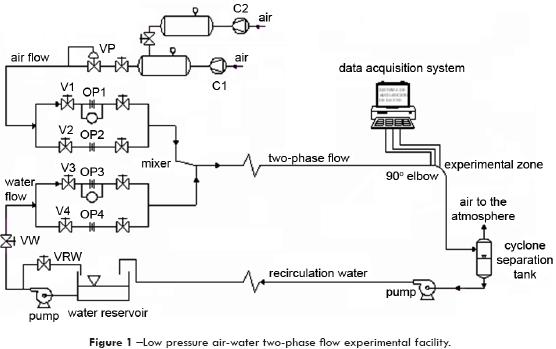
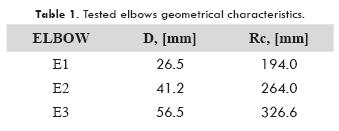
Three galvanized inconel alloy elbows were tested; their geometrical characteristics are presented on Table 1. Pressure taps were located 30 diameters upstream and downstream of the elbow where the fully developed flow condition was guaranteed; in figure 2 downstream details in the elbow are shown. Pressure taps were drilled each 15° on the internal and external elbow's walls, to measure static pressure variation as flow pass through the fitting. All pressure taps were connected to calibrated pressure transducers.

 

 

To locate the test zone the Mandhane chart and the values of U_SL and U_SG were used (Luna Reséndiz, 1998). The experimental set up capacity and stability allow testing velocities U_SG in a range from 15 to 35 m/s and U_SL from 0.36 to 3.27 m/s, which were slug flow conditions for a 26.5 mm internal diameter pipe.

 

Models Description

To address this problem, researchers (Lockhart and Martinelli, 1949; Dukler, et al, 1964; Chisholm, 1983; Wallis, 1969) have suggested some practical approaches for the elbow two-phase flow pressure drop evaluation, which can be used on engineering applications. These models can be classified in four basic groups: homogeneous model, separated flow model, dimensional and similitude approach and Chisholm Approach.

All these models are also called "black box or global approaches" because they do not make any reference to a specific flow pattern presented in the elbow. These approaches, with the exception of the homogeneous model, were developed using experimental data provided by several other authors, (Hetsroni, 1982).

 

Homogeneous model

This model assumes that the liquid and gas move at the same velocity, thus, it could be treated as a pseudo single-phase flow with pondered properties. The mixture properties are based on the volumetric proportion of each phase (Wallis, 1969). Homogeneous model based on a differential volume control momentum balance yields the following expression for the two-phase flow pressure drop (Wallis, 1969).

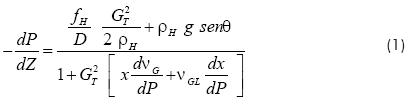
f_H, depends on the homogeneous flow Reynolds number and the relative roughness of the pipe's surface. The Reynolds number for the homogeneous mixture is defined as:

The mixture viscosity must be computed using the expression,

which depends on the homogeneous liquid volumetric fraction λ_L=Q_L/(Q_L+Q_G) and the homogeneous gas volumetric fraction λ_G=Q_G/(Q_L+Q_G), where λ_L+λ_G = 1.

 

Separated flow model (Lockhart - Martinelli approach)

Lockhart and Martinelli (1949) considered that both phases flow separately in the pipe. In addition, they suggested that the pressure drop in each phase in the mixture, must be equal to the pressure drop in the two-phase flow, in order to keep the system equilibrium (Lockhart and Martinelli, 1949),

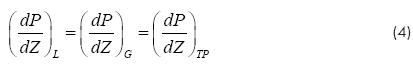
Using the above considerations, they developed the Martinelli's parameter given by,

X relates the pressure drop of liquid and gas phases when they flow alone in the full pipe. They also developed, the Martinelli's multiplier Φ_L, which relates the liquid pressure drop in the two phase flow mixture to the pressure drop of the liquid phase flowing alone in the pipe (Lockhart and Martinelli, 1949).

Using experimental data of several authors, Chisholm (1983) developed an algebraic correlation for Φ_L as a function of X.

With C = 20 for turbulent flow (liquid-gas), which is very common in two-phase flow industrial systems.

 

Dimensional and similitude analysis (Dukler approach)

Dukler proposed an approach based on a global dynamic similitude analysis, i.e., the relationship between the viscous, pressure and gravitational forces is considered to be the same in the model and in the prototype. For single-phase flows, the dynamic similitude between these forces exists when the Euler and the Reynolds numbers are equal in the model and in the prototype (Dukler, et al, 1964). Dukler proved that there is also a dynamic similitude in two-phase mixtures flowing in a pipe, and proposed the following expression:

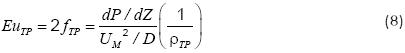
For f_TP , Dukler suggested a normalized ratio, f_TP/f₀, where, f₀, is the friction factor for the case when λ_L = 1 (using the same Reynolds number of the mixture).

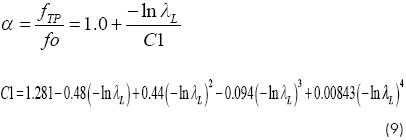
Finally, the equation to compute the two-phase flow pressure drop is

All above-mentioned approaches are simple and easy to program, they ¡ust require input variables such as the fluid properties, geometric characteristics of the pipe and the mass flow rate of both phases. All three methods were developed for straight pipes but they can be extended for pipe fittings using its equivalent straight pipe length (Le).

In a steady single-phase flow through a constant diameter pipe, the pressure gradient before and after the horizontal elbow are the same in both fully developed zones. The elbow's presence only shifts down the pipe pressure gradient after it, so the pressure drop due to the elbow is just the distance between the two shifted gradients (Cheremisinoff, 1986).

A similar analysis applies for two-phase flows; however, in this case the additional pressure drop is mainly due to the secondary flow formed in the elbow, the separation of the phases and the friction between them.

 

Chisholm approach.

Chisholm proposed a correlation, similar to the one used for single-phase flows. It involves dimensionless parameters obtained by correlating two-phase flow experimental data (Chisholm, 1983). The approach also requires a Le that depends on the elbow radius, the diameter pipe ratio (Rc/D), and the angle as well (Cheremisinoff, 1986). The increment of Le, as a function of Rc/D, is mainly due to the friction, the centrifugal force and the secondary flows present in the elbow. The pressure drop for single-phase in the elbow is:

In order to extend it for two-phase flow in horizontal elbows, Chisholm (1983) suggested evaluating the pressure drop coefficient by assuming that the whole two-phase flow mixture flows as liquid through the fitting. Therefore, this coefficient is expressed by:

Considering that the two-phase flow mixture, which flows as liquid phase, fills up the pipe, the pressure drop is ¡ust evaluated as:

The pressure drop in a two-phase mixture flowing through a 90° elbow is given by an expression that includes the mass quality and a correction factor for two-phase properties:

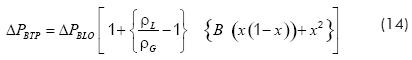
In this equation B includes the relative radius of the elbow,

 

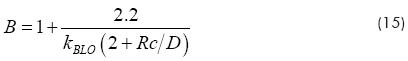
Results Analysis

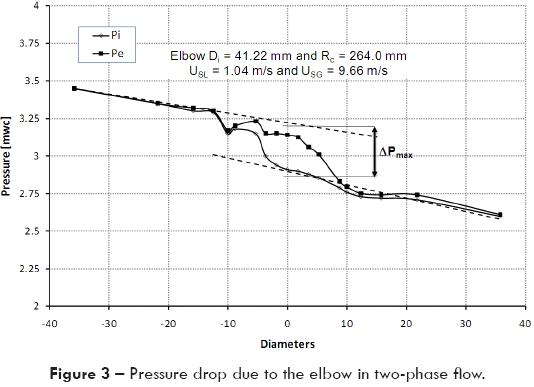
The two-phase flow pressure profile upstream and downstream elbow was plotted and the pressure drop was obtained for each experimental flow condition. Figure 3 shows the pressure profile and the pressure drop due to the elbow. In order to compare the two-phase flow models, all of them were programmed and computed under similar flow conditions as in experimental data.

 

In figures 4, 5, 6 the experimental results for each tested elbow are compared versus the results obtained with the four models using the same experimental conditions; ideally, the points should be aligned on the 1/1 slope. Using this criterion, it is possible to observe that both the Chisholm and Lockhart-Martinelli models fit better all the experimental results at low mixture velocities; however, they present a bigger dispersion when the mixture velocity augments. Another important thing to remark is that the data dispersion for E3 is bigger of all three tested elbows; this means that there is clear influence of the diameter. The reason could be that the flow pattern characteristics as the hold-up, among others, change with the pipe diameter, so this factor must be considered in the correlation.

 

 

 

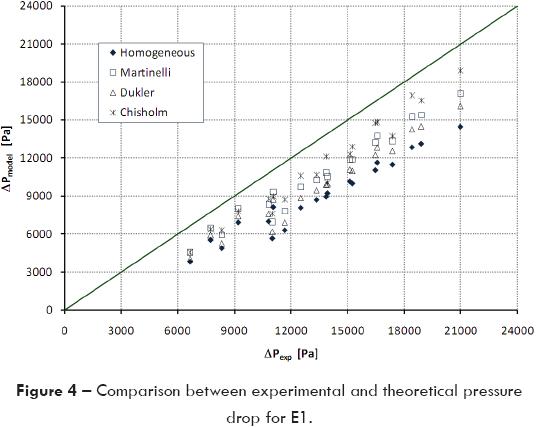
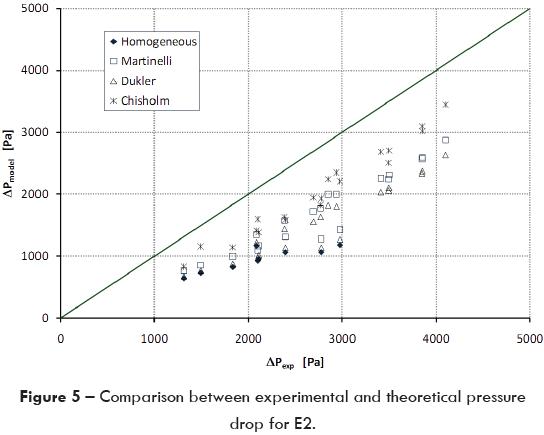
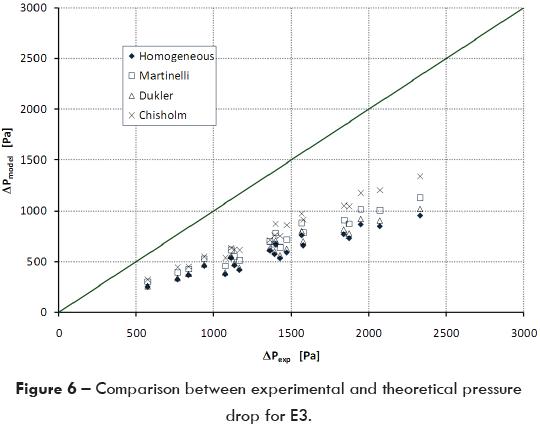
The Chisholm model provides the best results presenting an average variation from 18.2 to 42.1% respect to experimental data. Theoretically, gas content in mixture influences the pressure drop magnitude because a small increment in gas mass flow produces an important rise in both mixture velocity and void fraction. As a result, pressure drop augments because it is directly proportional to the square of the mixture velocity.

In figure 7 it is possible to observe a linear correlation between the mixture quality (x) and the liquid Martinelli's multiplier, which was obtained maintaining constant the mass liquid flow rate and varying the mass gas flow rate. The pressure drop increases as the quality augments.

 

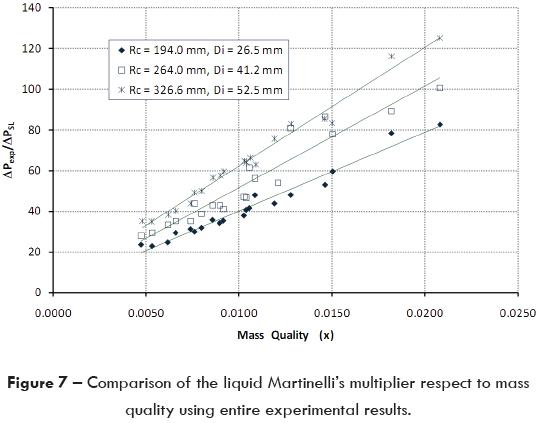
Data presented in figure 7 corresponds to all evaluated elbows, so it is possible to remark that by increasing m_T and x, the pressure drop in the elbow also augments. On the other hand, for the same flow rate conditions in all three elbows the pressure drop is bigger for the smaller diameter pipe, so the diameter pipe influence must be taken into account.

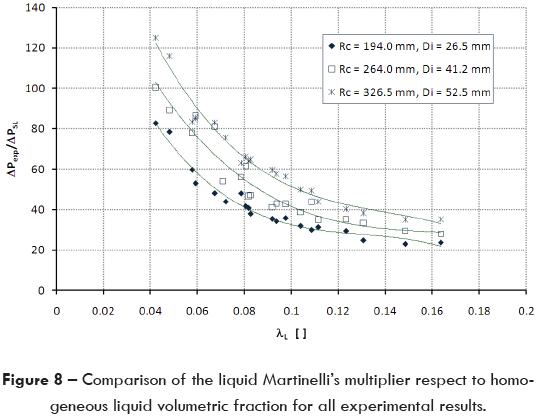
In figure 8 the experimental results obtained of the three elbows as a function of λ_L are presented. The liquid Martinelli's multiplier is plotted as a function of λ_L = (U_SL/U_M). It can be seen that as λ_L reduces, the 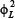augments; moreover, 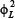increases, for the same two-phase flow conditions, as the elbow's diameter rises, and decreases as λ_L augments.

 

A comparison between the Chisholm approach and the entire experimental data is shown in figure 9. As was described above the Chisholm approach fitted better the experimental data with less dispersion than the other three models compared in this study. In this figure the pressure drop increases as the pipe diameter reduces and the mass flow rate augments, which is in agreement with the single-phase flow theory.

 

Figures 8, 9 and 10 yield the conclusion that there is a correlation between the Martinelli's multiplier, the mass quality of the mixture, the homogeneous volumetric fraction and the elbow curvature radius; therefore, the Dean number must be included in order to consider the diameter effect (Cheremisinoff, 1986).

 

 

Consequently, to improve the Chisholm model for a wider range of application is needed to find a dimensionless correlation as a function of λ_G and the Dean number. The proposed dimensionless group consists of λ_G times the Dean number to the n power, λ_G(De)ⁿ. This new parameter was plotted against the ratio between experimental pressure drop and the pressure drop given by the Chisholm approach (ΔP_exp/ΔP_BTP). The curve that best fitted the entire experimental data was determined, so the correction factor for the Chisholm theoretical model was obtained.

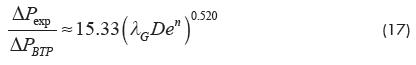
Figure 10 shows the pressure drop ratio versus the proposed parameter, given by the equation 17; it can be noticed that the correlation is quite good. Furthermore, the Dean number exponent was found to be n=-0.5, so from the equation (17) the adjusted Chisholm model is,

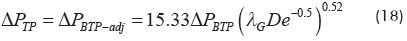
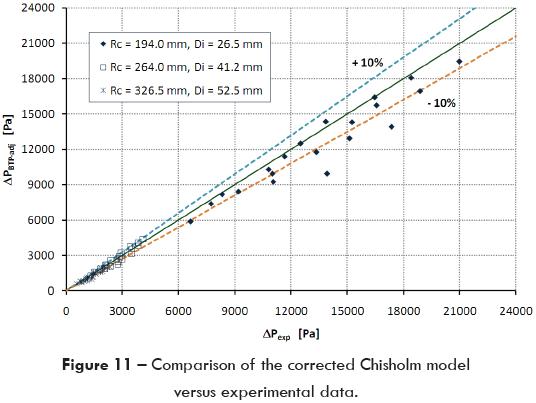
Equation 18 fits well the entire experimental data; moreover, it includes the Dean number in order to generalize the model application. The results obtained with the adjusted Chisholm approach are plotted in figure 11. The predictions using adjusted Chisholm model were improved presenting an average error of 8.66% with a standard deviation of 6.04 and an average dispersion of 4.79%.

 

In order to obtain an easier and accurate correlation, the pressure drop produced by the entire mixture flow, taken as a liquid ΔP_BLO, was used, i.e., the entire two-phase flow is considered as liquid flowing in the pipe and filling it up.

Therefore, a dimensionless group which includes the Dean number and the homogeneous volumetric fraction was developed, and the correlation found is,

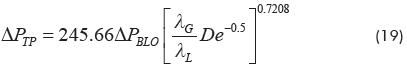
Using equation 19 a better correlation is obtained; figures 12 and 13 show the results of the correlation factor and the comparison with the experimental data. As can be seen, the proposed model (equation 19) gives better results with an average error of 7.75 %, with a standard deviation of 5.48 Pa and an average dispersion of 4.13%.

 

 

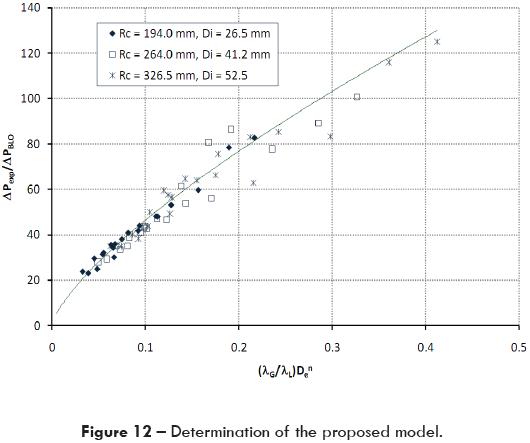
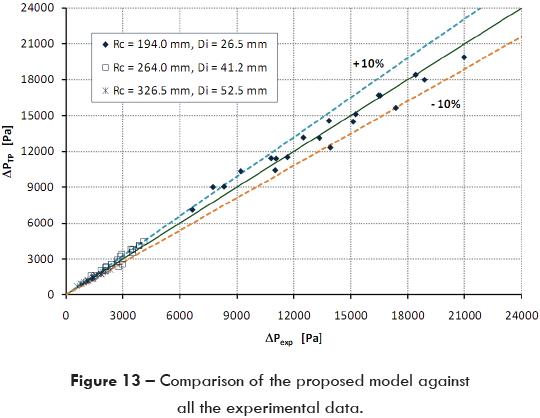
Figures 11 and 13 show the comparison of the corrected Chisholm model (equation 18) and the proposed model (equation 19) against experimental data. Because more data are within ± 10% error the proposed model predicted better the pressure drop for two-phase flow in a 90° horizontal elbow.

 

Conclusions

The results calculated by four models used to evaluate the two-phase flow pressure drop in elbows (Homogeneous, Lockhart-Martinelli, Dukler and Chisholm) were compared with the experimental data obtained in a two-phase flow horizontal rig. As was expected, the Chisholm approach was the model that best fit the experimental data, presenting a maximum average error of 42 % and a minimum of 18.3 %.

After analyzing the experimental results it was found that as λ_G increases, the liquid Martinelli's multiplier augments, and it decreases when λ_L rises. In addition, there is a clear influence of the pipe diameter which is in agreement with the single-phase flow theory. Another important fact that has to be considered is the correlation between the mass quality of the mixture and the liquid Martinelli's multiplier - as x increases the mixture velocity augments, consequently, Δp rises too.

As a final result of this work, two new correlations were developed. The first one is the Chisholm approach modified to reduce the dispersion, equation (18); the second one takes as a base the Δp produced by m_T when it is considered as a liquid, and is corrected by a factor which considers the λ_L and the Dean number (equation 19). Experimental data obtained of three different diameter elbows was compared with the results of these two final correlations. It was found that equation (19) gives better results with an average error of 7.75 %, a standard deviation of 5.48 Pa and an average dispersion of 4.1 3 %. Therefore, due to its simplicity and accuracy equation 19 is recommended for two-phase pressure drop evaluation in 90° horizontal elbows.

 

References

Azzi A., and Friedel L, "Two-phase upward flow 90° bend pressure loss model", Forschung im Ingenieurwesen Springer-Verlag, 69, pp. 120-130, 2005.         [ Links ]

British Standards Institution. BS 1042: Section 1.1, Methods of Measurement of Fluid Flow in Closed Conduits, Part 1. Pressure differential devices, 1981.         [ Links ]

Chan A. M., Maynard K. J., Ramundi J. and Wiklund E. Qualifying elbow meters for high pressure flow measurements in an operating nuclear power plant, International Conference on Nuclear Engineering, ICONE14, July 17-20, 2006, Miami, Florida.         [ Links ]

Cheremisinoff, N. P. (editor), Encyclopedia of Fluid Mechanics, Volume 3, Gas Liquid Flows, Gulf Publishing Company, 1986.         [ Links ]

Chisholm D., Two-Phase Flow in Pipelines and Heat Exchanges, Pitman Press, Ltd., 1983.         [ Links ]

Dukler A. E., Wicks, M. III and Cleveland, R. G.: "Frictional Pressure Drop in Two-Phase Flow: B. An Approach Through Similarity Analysis", AIChE Journal, vol. 10, No. 1, pp. 44-51, 1964.         [ Links ]

Hernández Ruíz J., Estudio del comportamiento de flujo de fluidos en tuberías curvas para aplicaciones en metrología, Tesis de Maestría, IPN-ESIME, 1998.         [ Links ]

Hetsroni, G. (editor), Handbook of Multiphase Systems, Hemisphere McGraw Hill, 1982.         [ Links ]

International Organization for Standardization. ISO 5167-1: 1998, Measurement of Fluid Flow by Means of Pressure Differential Devices, 1998.         [ Links ]

Kim Seungjin, Park Jung Han, Kojasoy Gunol and. Kelly Joseph M, Local interfacial structures in horizontal bubbly flow with 90-degree bend, International Conference on Nuclear Engineering paper, ICONE14, July 17-20, 2006, Miami, Florida.         [ Links ]

Kim Seungjin, Kojasoy Gunol and Guo Tangwen, "Two-phase minor loss in horizontal bubbly flow with elbows: 45° and 90° Elbows", Nuclear Engineering Design, 2008.         [ Links ]

Lockhart, R., W. and Martinelli, R., C. "Proposed Correlation of Data for Isothermal Two-Phase Two-Component Flow in Pipes", Chem. Eng. Prog., vol. 45, no. 1, pp. 39-48, 1949.         [ Links ]

Luna Reséndiz J. C., Estudio Comparativo de los Modelos que se Utilizan para Evaluar Pérdidas de Presión en Tuberías Curvas de 90° que Conducen Mezclas Bifásicas, Tesis de Maestría, IPN-ESIME, 2002.         [ Links ]

Mandal S. N. and Das S. K., Pressure Losses in Bends during Two-Phase Gas-Newtonian Liquid Flow, Ind. Eng. Chem. Res. 2001, 40, 2340-2351.         [ Links ]

Sánchez Silva F., Gómez A., Toledo M., Quinto P. and Zurita V., "Experimental And Numerical Curved Flow Study For Metrology Purposes", Journal of Applied Research and Technology, Vol. 1, No. 2, July, pp. 114-126, 2003.         [ Links ]

Savalaxs Supa-Amornkul, Frank R. Steward and Derek H. Lister, "Modeling Two-Phase Flow in Pipe Bends", Transactions of the ASME, Journal of Pressure Vessel Technology, Vol. 127, May, pp. 204-209, 2005.         [ Links ]

Wallis, G.B., One Dimensional Two-Phase Flow, McGraw-Hill, 1969.         [ Links ]